Рисуем морозные узоры на SQL

Немного SQL-магии под катом: математика, рекурсия, псевдографика.

Вспоминаем под Новый год формулу угла между векторами:

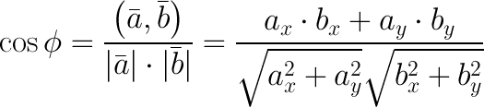
WITH RECURSIVE T AS (
  SELECT
    0 x
  , 0 y
  , '{"{0,0}"}'::text[] c -- растим узор от центра
  , 0 i
UNION ALL
  (
    WITH Z AS (
      SELECT
        dn.x
      , dn.y
      , T.c
      , T.i
      FROM
        T
        -- вбрасываем случайную точку на плоскость
      , LATERAL(
          SELECT
            ((random() * 2 - 1) * 100)::integer x
          , ((random() * 2 - 1) * 100)::integer y
        ) p
        -- из всех существующих точек выбираем у ней ближайшую
      , LATERAL(
          SELECT
            *
          FROM
            (
              SELECT
                (unnest::text[])[1]::integer x
              , (unnest::text[])[2]::integer y
              FROM
                unnest(T.c::text[])
            ) T
          ORDER BY
            sqrt((x - p.x) ^ 2 + (y - p.y) ^ 2)
          LIMIT 1
        ) n
        -- из 8 ее "целочисленных" соседей заполняем ближайшую по направлению к вброшенной
      , LATERAL (
        SELECT
          n.x + dx x
        , n.y + dy y
        FROM
          generate_series(-1, 1) dx
        , generate_series(-1, 1) dy
        WHERE
          (dx, dy) <> (0, 0)
        ORDER BY
          CASE
            WHEN (p.x, p.y) = (n.x, n.y) THEN 0
            ELSE abs(acos(((p.x - n.x) * dx + (p.y - n.y) * dy) / sqrt((p.x - n.x) ^ 2 + (p.y - n.y) ^ 2) / sqrt(dx ^ 2 + dy ^ 2)))
          END
        LIMIT 1
      ) dn
    )
    SELECT
      Z.x
    , Z.y
    , Z.c || ARRAY[Z.x, Z.y]::text
    , Z.i + 1
    FROM
      Z
    WHERE
      Z.i < (1 << 10)
  )
)
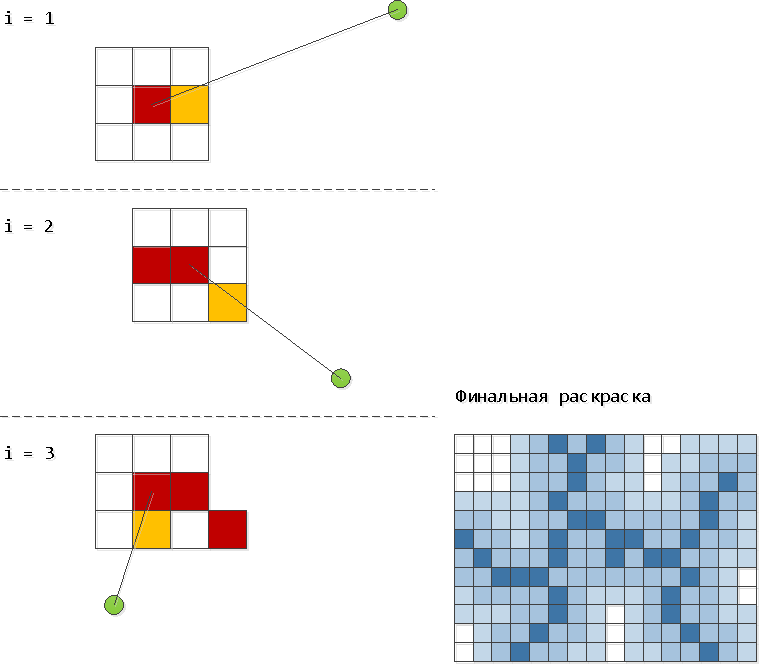
-- для каждой точки рисунка вычисляем расстояние до узора
, map AS (
  SELECT
    gx x
  , gy y
  , (
      SELECT
        sqrt((gx - T.x) ^ 2 + (gy - T.y) ^ 2) v
      FROM
        T
      ORDER BY
        v
      LIMIT 1
    ) v
  FROM
    generate_series(-40, 40) gx
  , generate_series(-30, 30) gy
)
-- формируем алфавит отрисовки
, gr AS (
  SELECT
    regexp_split_to_array('#*+-. ', '') s
)
-- рисуем картинку
SELECT
  string_agg(
    coalesce(s[(v * (array_length(s, 1) - 1))::integer + 1], ' ')
  , ' '
  ORDER BY x) frozen
FROM
  (
    SELECT
      x
    , y
    , v::double precision / max(v) OVER() v -- нормируем значения расстояний по максимуму
    FROM
      map
  ) T
, gr
GROUP BY
  y
ORDER BY
  y;

Автор: Боровиков Кирилл

Источник