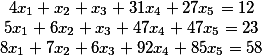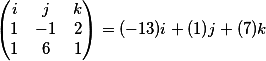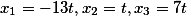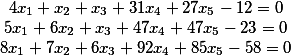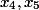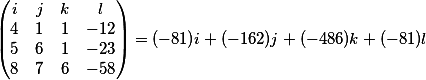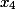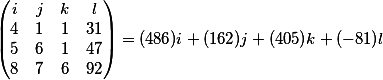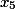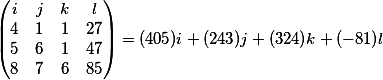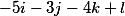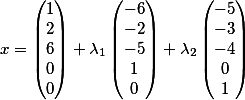Добрый день!
В данной статье я попробую взглянуть по новому на алгоритм поиска общего решения системы линейных уравнений.
Задача, которой мы займемся звучит так.
Найти общее решение следующей системы уравнений
Такую задачу решают, приведя исходную систему к треугольному виду по методике Гаусса. Потом выбрав свободные переменные вычисляют общее решение.
Я хочу показать, как можно решать подобные системы другим способом. Насколько она известна и применяется где либо, я узнать не смог. Во всех публичных/популярных материалах, используется метод Гаусса.
Сразу скажу что решение конечно же не оптимально (по быстродействию), так как при вычислении векторного произведения, надо вычислять определитель матрицы, а это так или иначе вычисление треугольной матрицы.
Но решение красиво и наглядно, кроме этого легко видеть критерий при котором система не имеет решений.
В чем же суть методики?
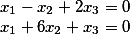
Решая эту систему как произведение двух векторов, мы получим
А следовательно, корни системы равны
Для тех кто не верит, это легко проверяется подстановкой
Используем этот прием и рассмотрим, как же решаются такие системы с помощью векторных произведений.
Итак, у нас есть исходная система
Перенесем свободные члены в левую часть
У нас получилось 6 столбцов.
На этом этапе не будем вводить новых сущностей и не используем в своей работе понятия ранга матрицы. (Прошу отнестись снисходительно)
Мы просто видим что уравнений 3, а переменных 5-ть. Следовательно общее решение будет использовать 5-3=2 независимых переменных.
На этом же шаге, мы можем определить, какие же из переменных будут свободными. Возьмем две переменных, которые будут правее всех, и назначим их свободными.
Note: Для других уравнений не всегда получается, что надо брать именно последние правые коэффициенты
А теперь за три шага определяем фундаментальное решение исходной системы
Шаг 1. Здесь последняя колонка это свободные члены системы
Шаг 2. Здесь последняя колонка это коэффициенты при переменной
Шаг 3. Здесь последняя колонка это коэффициенты при переменной
Нет необходимости подробно рассказывать откуда мы берем данные. Я думаю для читающих это очевидно. (Кто решал систему уравнений методом Крамера, найдут общие черты)
Интереснее то, что мы с этими «векторами» делать будем.
Разделим их на -81
получаем следующие три вектора
выстроим их в вертикаль и таким образом фундаментальное решение принимает вид
Великолепно! Не правда ли…
Для критерия разрешимости заданной системы уравнений в большинстве случаев используется правило Кронекера-Копелли, здесь же просто анализируется результат векторного произведения.
Если результирующий вектор имеет вид
где 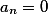
Если результирующий вектор имеет все нулевые коэффициенты, то это говорит о том, что или как минимум одно из уравнений есть линейное представление другого, и/или одна из переменных пропорциональна другой.
Эта статья первая, и хотелось бы услышать замечания, критику, пожелания в свой адрес.
Алгоритм и калькулятор создан еще в январе 2019 года и только сегодня я решил опубликовать информацию на Хабре.
Если примете в свой коллектив/общество, то следующая тема будет
— как находить общее решение системы диофантовых уравнений.
Автор: Дмитрий Варламов