К сожалению, адекватно перевести название затеянного мной безобразия на русский язык оказалось не просто. С удивлением я обнаружил, что официальная документация MSDN называет "дженерики" "шаблонами" (по аналогии с C++ templates, я полагаю). В попавшемся мне на глаза 4-м издании "CLR via C#" Джеффри Рихтера, переведенном издательством "Питер", дженерики именуются "обобщениями", что гораздо лучше отражает суть понятия. В этой статье речь пойдет о небезопасных обобщенных математических операциях в C#. Учитывая, что C# не предназначен для высокопроизводительных вычислений (хотя, безусловно, на это способен, но не в состоянии тягаться с тем же C/C++), математическим операциям в BCL уделено не так много внимания. Давайте попробуем упростить работу с базовыми арифметическими типами силами C# и CLR.
Постановка задачи
Дисклеймер: в статье будет много фрагментов кода, часть из которых я проиллюстрирую ссылками на прекрасный ресурс SharpLab (GirHub) авторства Андрея Щёкина.
Большинство вычислений так или иначе сводится к базовым операциям. Сложение, вычитание (инверсия, отрицание), умножение и деление можно дополнить операциями сравнения и проверкой на равенство. Разумеется, все эти действия можно легко и просто выполнить над переменными любых базовых арифметических типов C#. Единственная проблема — C# должен знать на этапе компиляции, что операции выполняются над конкретными типами, и создается впечатление, что написать метод, который одинаково эффективно (и прозрачно) складывает два целых числа и два числа с плавающей точкой — невозможно.
Давайте конкретизируем наши пожелания к гипотетическому обобщенному методу, выполняющему какую-либо простейшую математическую операцию:
- Метод должен иметь ограничения обобщенного типа, защищающие нас от попытки сложения (или умножения, деления) двух произвольных типов. Нам нужен некий generic type constraint.
- Для чистоты эксперимента, принимаемые и возвращаемые типы должны быть одинаковыми. Например, бинарный оператор должен иметь сигнатуру вида
(T, T) => T. - Метод должен быть хотя бы частично оптимизирован. Например, повсеместная упаковка (boxing) неприемлема.
А что там у соседей?
Давайте посмотрим на F#. Я не силен в F#, но большинство ограничений C# продиктовано ограничениями CLR, а значит F# страдает от тех же проблем. Можно попробовать объявить явный обобщенный метод сложения и обычный метод сложения и посмотреть, что система вывода типов F# скажет на это:
let add_gen (x : 'a) (y : 'a) =
x + y
let add x y =
x + y
add_gen 5.0 6.0 |> ignore
add 5.0 6.0 |> ignoreВ данном случае оба метода окажутся необобщенными, и сгенерирированный код будет идентичным. С учетом жесткости системы типов F#, где отсутствуют неявные преобразования вида int -> double, после первого вызова этих методов с параметрами типа double (в терминах C#), вызвать методы с параметрами других типов (даже с возможной потерей точности за счет преобразования типа) больше не удастся.
Стоит отметить, что если заменить оператор + на оператор равенства =, картина становится несколько иной: оба метода превращаются в обобщенные (с точки зрения C#), а для выполнения сравнения вызывается специальный метод-хэлпер, доступный в F#.
let eq_gen (x : 'a) (y : 'a) =
x = y
let eq x y =
x = y
eq_gen 5.0 6.0 |> ignore
eq_gen 5 6 |> ignore
eq 5.0 6.0 |> ignore
eq 5 6 |> ignoreЧто насчет Java?
Про Java мне говорить сложно, но, насколько я могу судить, значимые типы там отсутствуют в привычном для нас виде, но все же есть примитивные типы. Для работы с примитивами в Java есть обертки (например, ссылочный Long для примитивного by-value long), которые имеют общий базовый класс Number. Таким образом, частично обобщить операции можно иcпользуя Number, но это ссылочный тип, что вряд ли положительно скажется на производительности.
Поправьте меня если я не прав.
C++?
C++ — язык для читеров.
C++ открывает путь к таким возможностям, которые кое-кто считает… неестественными.
Шаблоны (aka templates), в отличие от обобщений (generics), являются, в прямом смысле, шаблонами. При объявлении шаблона можно явно ограничить типы, для которых этот шаблон доступен. По этой причине, в C++ валиден, например, такой код:
#include <iostream>
template<typename T, std::enable_if_t<std::is_arithmetic<T>::value>* = nullptr>
T Add (T left, T right)
{
return left + right;
}
int main()
{
std::cout << Add(5, 6) << std::endl;
std::cout << Add(5.0, 6.0) << std::endl;
// std::cout << Add("a", "b") << std::endl; Does not compile
}is_arithmetic, к сожалению, допускает и char, и bool в качестве параметров. С другой стороны, char может быть эквивалентен sbyte в терминологии C#, хотя фактические размеры целочисленных типов зависят от платформы/компилятора/фазы луны.
Языки с динамической типизацией
Напоследок рассмотрим пару динамически типизированных (и интерпретируемых) языков, заточенных под вычисления. У таких языков обычно обобщение вычислений проблем не вызывает: если тип параметров подходит для выполнения, условно, сложения, то операция будет выполнена, иначе — падение с ошибкой.
В Python (3.7.3 x64):
def add (x, y):
return x + y
type(add(5, 6))
# <class 'int'>
type(add(5.0, 6.0))
# <class 'float'>
type(add('a', 'b')
# <class 'str'>В R (3.6.1 x64)
add <- function(x, y) x + y
# Or typeof()
vctrs::vec_ptype_show(add(5, 6))
# Prototype: double
vctrs::vec_ptype_show(add(5L, 6L))
# Prototype: integer
vctrs::vec_ptype_show(add("5", "6"))
# Error in x + y : non-numeric argument to binary operatorОбратно, в мир C#: ограничиваем обобщенный тип математической функции
К сожалению, этого сделать мы не можем. В C# примитивные типы являются значимыми типами (by-value), т.е. структурами, которые, хоть и унаследованы от System.Object (и System.ValueType), не имеют между собой много общего. Естественным и логичным ограничением выглядит where T : struct. Начиная с C# 7.3 нам доступно ограничение where T : unmanaged, которое означает, что T это неуправляемый тип, не являющийся указателем и не принимающий значение null. Этим требованиям удовлетворяют, кроме необходимых нам примитивных арифметических типов, еще и char, bool, decimal, любой Enum и любая структура, все поля которой имеют такой-же unmanaged-тип. Т.е. вот такой тип пройдет проверку:
public struct Coords<T> where T : unmanaged
{
public T X;
public T Y;
}Таким образом, мы не можем написать обобщенную функцию, принимающую только желаемые арифметические типы. Отсюда и Unsafe в заголовке статьи — нам придется положиться на программистов, использующих наш код. Попытка вызова гипотетического обобщенного метода T Add<T>(T left, T right) where T : unmanaged будет приводить к непредсказуемым результатам, если программист передаст в качестве аргументов объекты несовместимого типа.
Эксперимент первый, наивный: dynamic
dynamic является первым и очевидным инструментом, который может помочь нам решить нашу задачу. Разумеется, использовать dynamic для вычислений абсолютно бесполезно — dynamic эквивалентен object, а вызываемые методы с dynamic-переменной превращаются компилятором в монструозную рефлексию. В качестве бонуса — упаковка/распаковка наших by-value типов. Вот вам пример:
public class Class {
public static void Method() {
var x = Add(5, 6);
var y = Add(5.0, 6.0);
}
private static dynamic Add(dynamic left, dynamic right)
=> left + right;
}Достаточно взглянуть на IL метода Method:
.method public hidebysig static
void Method () cil managed
{
// Method begins at RVA 0x2050
// Code size 53 (0x35)
.maxstack 8
IL_0000: ldc.i4.5
IL_0001: box [System.Private.CoreLib]System.Int32
IL_0006: ldc.i4.6
IL_0007: box [System.Private.CoreLib]System.Int32
IL_000c: call object Class::Add(object, object)
IL_0011: pop
IL_0012: ldc.r8 5
IL_001b: box [System.Private.CoreLib]System.Double
IL_0020: ldc.r8 6
IL_0029: box [System.Private.CoreLib]System.Double
IL_002e: call object Class::Add(object, object)
IL_0033: pop
IL_0034: ret
} // end of method Class::MethodЗагрузил 5, упаковал, загрузил 6, упаковал, вызвал object Add(object, object).
Вариант явно нам не подходит.
Эксперимент второй, "в лоб"
Ладно, dynamic это не для нас, но ведь количество наших типов конечно, и они известны заранее. Давайте вооружимся ломом ветвлением и так и запишем: если тип наш, вычислим что-нибудь, иначе — вот вам исключение.
public static T Add<T>(T left, T right) where T : unmanaged
{
if(left is int i32Left && right is int i32Right)
{
// ???
}
// ...
throw new NotSupportedException();
}Ииии тут мы натыкаемся на проблему. Если понять, с какими типами мы работаем, еще можно, применить к ним операцию — тоже, то полученный условный int нужно преобразовать в неизвестный тип T и сделать это не очень просто. Вариант return (T)(i32Left + i32Right) не компилируется — нет гарантии, что T это int (хоть мы-то знаем, что это так). Можно попробовать двойное преобразование return (T)(object)(i32Left + i32Right). Сначала сумма упаковывается, затем — распаковывается в T. Это будет работать только если типы до упаковки и после упаковки совпадают. Нельзя упаковать int, а распаковать в double, даже если существует неявное преобразование int -> double. Проблема такого кода — гигантское ветвление и обилие упаковок-распаковок, даже в if условиях. Этот вариант тоже не годится.
Рефлексия и метаданные
Ну, поиграли и хватит. Все же знают, что в C# существуют операторы, которые можно переопределить. Вон, есть +, -, ==, != и так далее. Все, что нам нужно — вытащить по типу T статический метод, соответствующий оператору, например, сложения — и все. Ну да, снова пара упаковок, но уже никакого ветвления и никаких проблем. Все это дело можно закэшировать по типу T и вообще всячески ускорить процесс, сведя одну математическую операцию к вызову единственного метода рефлексии. Ну как-то так:
public static T Add<T>(T left, T right) where T : unmanaged
{
// Simple example without cache.
var method = typeof(T)
.GetMethod(@"op_Addition", new [] {typeof(T), typeof(T)})
?.CreateDeleate(typeof(Func<T, T, T>)) as Func<T, T, T>;
return method?.Invoke(left, right)
?? throw new InvalidOperationException();
}К сожалению, это не работает. Дело в том, что у арифметических типов (но не decimal) нет такого статического метода. Все операции реализованы посредством IL-операций, таких как add. Обычной рефлексией нашу проблему не решить.
System.Linq.Expressions
Решение на основе Expressions описано в блоге Джона Скита вот здесь (автор — Marc Gravell).
Идея довольно простая. Пусть у нас есть тип T, который поддерживает операцию +. Давайте создадим выражение примерно такого вида:
(x, y) => x + y;После чего, закэшировав, будем его использовать. Построить такое выражение довольно легко. Нам нужно два параметра и одна операция. Так и запишем.
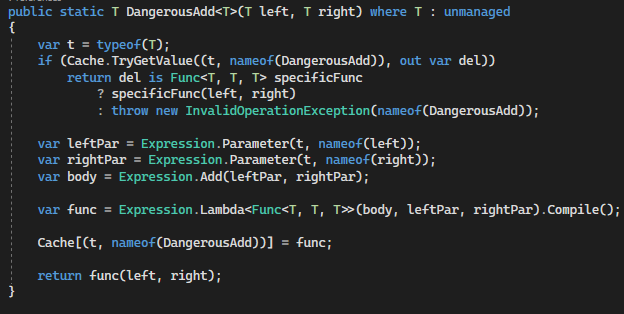
private static readonly Dictionary<(Type Type, string Op), Delegate> Cache =
new Dictionary<(Type Type, string Op), Delegate>();
public static T Add<T>(T left, T right) where T : unmanaged
{
var t = typeof(T);
// If op is cached by type and function name, use cached version
if (Cache.TryGetValue((t, nameof(Add)), out var del))
return del is Func<T, T, T> specificFunc
? specificFunc(left, right)
: throw new InvalidOperationException(nameof(Add));
var leftPar = Expression.Parameter(t, nameof(left));
var rightPar = Expression.Parameter(t, nameof(right));
var body = Expression.Add(leftPar, rightPar);
var func = Expression.Lambda<Func<T, T, T>>(body, leftPar, rightPar).Compile();
Cache[(t, nameof(Add))] = func;
return func(left, right);
}Полезная информация о деревьях выражений и делегатах была опубликована на хабре здесь.
Технически, выражения позволяют решить все наши проблемы — любую базовую операцию можно свести к вызову обобщенного метода. Любую более сложную операцию можно точно так же написать, используя более сложные выражения. Этого почти достаточно.
Нарушаем все правила
А можно ли добиться чего-то еще, используя силы CLR/C#? Давайте посмотрим, какой год генерирут методы сложения для разных типов:
public class Class
{
public static double Add(double x, double y) => x + y;
public static int Add(int x, int y) => x + y;
// Decimal only to show difference
public static decimal Add(decimal x, decimal y) => x + y;
}Соответствующий IL-код содержит один и тот же набор инструкций:
ldarg.0
ldarg.1
add
retЭто — тот самый op-код add, в который компилируется сложение арифметических примитивных типов. decimal в этом месте вызывает static decimal decimal.op_Addition(decimal, decimal). А что если написать метод, который будет обобщенным, но содержать именно этот IL-код? Ну, Джон Скит предупреждает, что так делать не стоит. В его случае он рассматривает все типы (включая decimal), а так же их nullable-аналоги. Это потребует довольно нетривиальных IL-операций и обязательно приведет к ошибке. Но мы все же можем попробовать реализовать базовые операции.
К моему удивлению, Visual Studio не содержит шаблонов для IL-проектов и IL-файлов. Нельзя просто взять и описать часть кода в IL и включить в свою сборку. Естественно, open source приходит нам на помощь. Проект ILSupport содержит шаблоны IL-проектов, а так же набор инструкций, которые можно добавить в *.csproj для включения IL-кода в проект. Разумеется, описывать в IL все — довольно сложно, поэтому автор проекта использует встроенный атрибут MethodImpl с флагом ForwardRef. Этот атрибут позволяет объявить метод как extern и не описывать тело метода. Выглядит примерно так:
[MethodImpl(MethodImplOptions.ForwardRef)]
public static extern T Add<T>(T left, T right) where T : unmanaged;Следующий шаг — в файле *.il с IL-кодом написать реализацию метода:
.method public static hidebysig !!T Add<valuetype .ctor (class [mscorlib]System.ValueType modreq ([mscorlib]System.Runtime.InteropServices.UnmanagedType)) T>(!!T left, !!T right) cil managed
{
.param type [1]
.custom instance void System.Runtime.CompilerServices.IsUnmanagedAttribute::.ctor()
= (01 00 00 00 )
ldarg.0
ldarg.1
add
ret
}Нигде явно не обращаясь к типу !!T, мы предлагаем CLR сложить два аргумента и вернуть результат. Здесь отсутствуют любые проверки типов и все на совести разработчика. Удивительно, но это работает, и относительно быстро.
Немного бенчмарка
Наверное, честный бенчмарк был бы построен на каком-то достаточно сложном выражении, вычисление которого "в лоб" сравнивалось бы с вот этими опасными IL-методами. Я написал простой алгоритм, который суммирует квадраты заранее вычисленных и сохраненных в массив double чисел и делит конечную сумму на количество чисел. Для выполнения операции я использовал C# операторы +, * и /, как это делают здоровые люди, функции, построенные с помощью Expressions, и IL-функции.
BenchmarkDotNet=v0.12.0, OS=Windows 10.0.18362
Intel Core i7-2700K CPU 3.50GHz (Sandy Bridge), 1 CPU, 8 logical and 4 physical cores
.NET Core SDK=3.1.100
[Host] : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT
Job-KYNFOO : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT
Runtime=.NET Core 3.1
| Method | N | Mean | Error | StdDev | Ratio | RatioSD |
|---|---|---|---|---|---|---|
| DirectSum | 1000 | 2.111 us | 0.0067 us | 0.0056 us | 1.00 | 0.00 |
| ExpressionSum | 1000 | 146.939 us | 2.7261 us | 2.5500 us | 69.77 | 1.15 |
| UnsafeSum | 1000 | 5.005 us | 0.0051 us | 0.0040 us | 2.37 | 0.01 |
| DirectSum | 10000 | 20.972 us | 0.0605 us | 0.0536 us | 1.00 | 0.00 |
| ExpressionSum | 10000 | 1,470.103 us | 3.4754 us | 3.0809 us | 70.10 | 0.26 |
| UnsafeSum | 10000 | 50.242 us | 0.0690 us | 0.0539 us | 2.40 | 0.01 |
| DirectSum | 100000 | 209.800 us | 0.7586 us | 0.6334 us | 1.00 | 0.00 |
| ExpressionSum | 100000 | 13,901.483 us | 163.6961 us | 153.1214 us | 66.38 | 0.71 |
| UnsafeSum | 100000 | 502.135 us | 0.3592 us | 0.3184 us | 2.39 | 0.01 |
| DirectSum | 1024000 | 2,306.182 us | 32.1166 us | 30.0419 us | 1.00 | 0.00 |
| ExpressionSum | 1024000 | 143,463.327 us | 1,309.2435 us | 1,224.6672 us | 62.22 | 1.03 |
| UnsafeSum | 1024000 | 5,276.843 us | 17.0845 us | 13.3384 us | 2.29 | 0.03 |
Наш небезопасный код примерно в 2.5 раза медленнее (в пересчете на одну опперацию). Связать это можно с тем фактом, что в случае вычисления "в лоб" компилятор компилирует a + b в op-код add, а в случае с небезопасным методом происходит вызов статической функции, что естественно медленнее.
Вместо заключения: когда true != true
Несколько дней назад я наткнулся на такой твит Джареда Парсонса:
There are cases where the following will print "false"
bool b =…
if (b) Console.WriteLine(b.IsTrue());
Это был ответ на вот эту запись, где показан код проверки bool на true, который выглядит примерно так:
public static bool IsTrue(this bool b)
{
if (b == true)
return true;
else if (b == false)
return false;
else
return !true && !false;
}Проверки кажутся избыточными, да? Джаред привел контр-пример, который демонстрирует некоторые особенности поведения bool. Идея заключается в том, что bool это byte (sizeof(bool) == 1), при этом false соответствуте 0, а true соответствует 1. Пока вы не размахиваете указателями, bool ведет себя однозначно и предсказуемо. Однако, как показал Джаред, можно создать bool, используя 2 в качестве начального значения, и часть проверок выполнится некорректно:
bool b = false;
byte* ptr = (byte*)&b;
*ptr = 2;Аналогичного эффекта мы можем добиться с помощью наших небезопасных математических операций (это не работает с Expressions):
var fakeTrue = Subtract<bool>(false, true);
var val = *(byte*)&fakeTrue;
if(fakeTrue)
Assert.AreNotEqual(fakeTrue, true);
else
Assert.Fail("Clause not entered.");Да-да, мы внутри true-ветки проверяем, является ли условие true, и ожидаем, что на самом деле оно не равно true. Почему это так? Если вы без проверок вычтите из 0 (=false) 1 (=true), то для byte это будет равно 255. Естественно, 255 (наш fakeTrue) не равно 1 (настоящий true), поэтому assert выполняется. Ветвление же работает по-другому.
Происходит инверсия if: вставляется условный переход; если условие ложно, то происходит переход в точку после окончания if-блока. Проверка выполняется оператором brfalse/brfalse_S. Он сравнивает последнее значение на стэке с нулем. Если значение равно нулю, то это false, перешагиваем через if-блок. В нашем случае fakeTrue как раз и не равен нулю, поэтому проверку проходит и выполнение продолжается внутри if-блока, где мы сравниваем fakeBool с настоящим значением true и получаем отрицательный результат.
Автор: Ilia
