Представьте, что вас окружает бесконечно высокая стена, а о том, что находится за стеной абсолютно ничего неизвестно. Теперь представьте, что олицетворением данной стены является вот это уравнение:
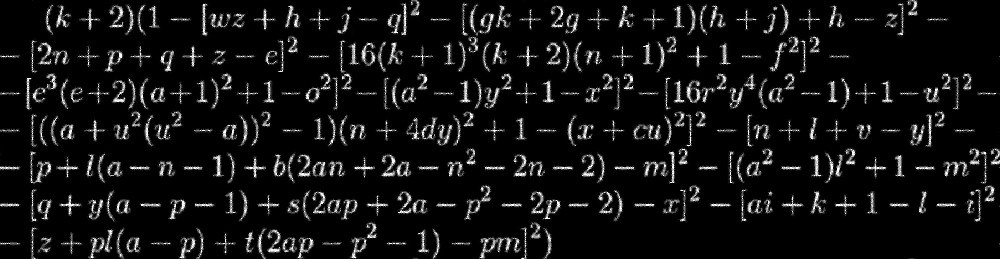
Эту метафору будет проще понять, если провести аналогию с черной дырой: мы не знаем, что находится под ее горизонтом событий, и чтобы это узнать нам нужно придумать способ, как туда добраться. Нечто подобное существует в мире математики. Данное уравнение — это настоящая «формула» простого числа, но чтобы ею пользоваться, нам нужно придумать, как искать подходящие {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, w, v, x, y, z}.
Черная дыра и данное уравнение — это предельные состояния чего-то реального и абстрактного. И, если о первом существует достаточно догадок и представлений, то о втором, практически ничего не известно. Но, что если это действительно «математическая» черная дыра. Разве вам не интересно что может произойти, если мы попадем
Из чего состоит стена?
Числа — их нет в реальном мире. Бывает семь игральных костей, семь атомов, семь смертных грехов, но самой по себе семерки не существует — это абстракция. Да, мы бы могли сказать, что числа — это просто множество абстрактных объектов, однако, это целый мир. Мир, в котором, как и в мире реальном, существуют свои законы. Сама мысль об этом кажется очень странной. Тем не менее, существование такого раздела математики, как теория чисел, говорит о том, что эта «странность» очень важна для нас.
Самым волнительным является то, что среди этих воображаемых объектов есть особенные — простые числа. Они как детерминированный хаос — предсказуемы и непредсказуемы одновременно, в зависимости от масштаба их рассмотрения. Например, находясь рядом с ними, мы можем заметить, что их количество перед некоторым произвольным числом n, не превзойдет:
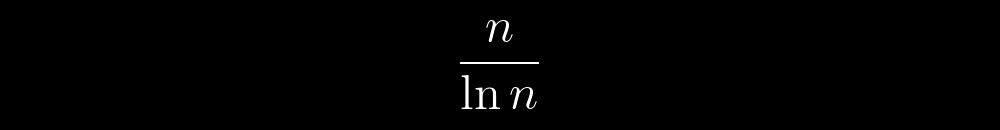
Меняя масштаб, мы начинаем замечать очень много намеков на какие-то внутренние правила их поведения. Постепенно этих намеков становится слишком много. Все чаще и чаще звучат вопросы «Откуда они вообще могли взяться?», «А что если существует некий алгоритм получения простых чисел?», «А что если каждое простое число может быть получено с помощью одного и того же алгоритма?»
Как появилась стена
Если некоторая последовательность чисел получается в результате работы некоторого алгоритма, то множество чисел данной последовательности считается перечислимым, даже, несмотря на то, что оно может быть бесконечно большим. Перечислимые множества обладают одним замечательным свойством — диофантовостью. Это значит, что любое такое множество может быть представлено диофантовым уравнением — полиномом с целыми положительными коэффициентами и степенями.
Следующее заявление может показаться абсолютно неправдоподобным, но, исходя из такого определения, мы можем утверждать, что все ключи безопасности и значения хеш-функций (даже биткоины) могут быть выражены через диофантовы уравнения. т.е. уравнения, которые решаются в целых числах. И да, теоретически, кто-то может узнавать любые секреты, быть бесконечно богатым и влиятельным человеком. Но, для того, чтобы стать таким человеком, эти уравнения надо сначала вывести, а потом решить.
С задачей представления множества диофантовым уравнением, частично или полностью, может справиться компьютер. Но здесь появляется другая проблема — диофантовы уравнения не решаются в общем виде, т.е. какой-то единый алгоритм их решения отсутствует. Это не кажется большой проблемой, потому что мы знаем, что некоторые уравнения выделяются в отдельные виды, для решения которых, уже найдены эффективные методы.
Но даже несмотря на наличие этих методов, мы неизбежно сталкиваемся с вычислительными трудностями, которые связаны либо с точностью вычислений, либо со скоростью выполнения итераций.
Как же так получилось, что простые числа оказались перечислимы? Сам процесс создания уравнений, представляющих перечислимые множества, опирается на основания математики — арифметику и логику. И если мы имеем достаточно знаний о свойствах объектов некоторого множества, то, опираясь на эти знания, мы можем делать предположения об алгоритме, который позволяет их получать. И, как оказалось, знаний о свойствах простых чисел было накоплено достаточно для этой цели. Уравнение было получено, и теперь все вопросы, связанные с простыми числами, сводятся к нему одному.
Но мы не можем его решить.
Толщина и прочность стены
Фактически, нам брошен вызов. И нам заранее известно о неизбежном поражении. Возможно, отступление было бы самым благоразумным решением. Но разве нам не нужны эти поражения, чтобы превзойти себя? Давайте хоть чуть-чуть попытаемся его решить.
Взглянем на уравнение еще раз:
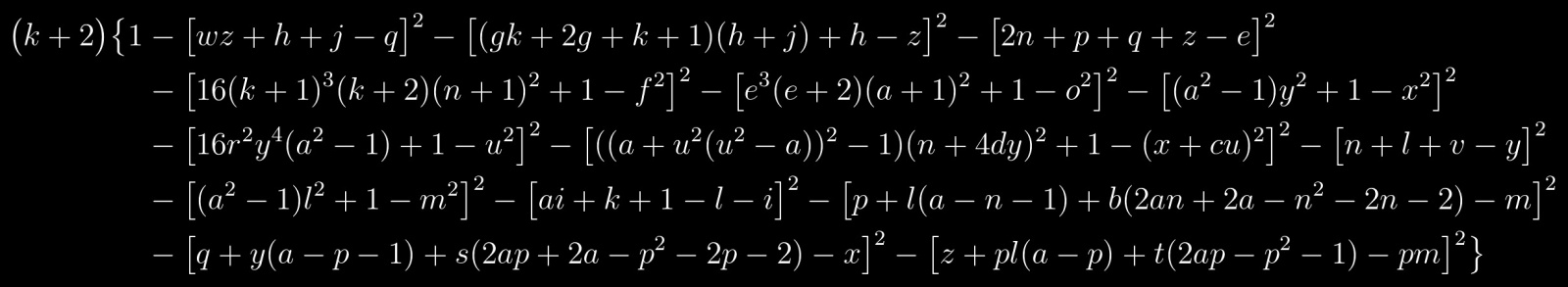
Это полином, множество положительных значений которого совпадает с множеством простых чисел. Он состоит из двух сомножителей: левый множитель будет простым числом лишь тогда, когда правый множитель, обозначенный фигурными скобками, будет равен единице, а это, в свою очередь, возможно, только если каждое слагаемое в данном множителе, обозначенное квадратными скобками, будет равно нулю. Получается, что вопрос о решении данного уравнения сводится к решению системы следующих уравнений:
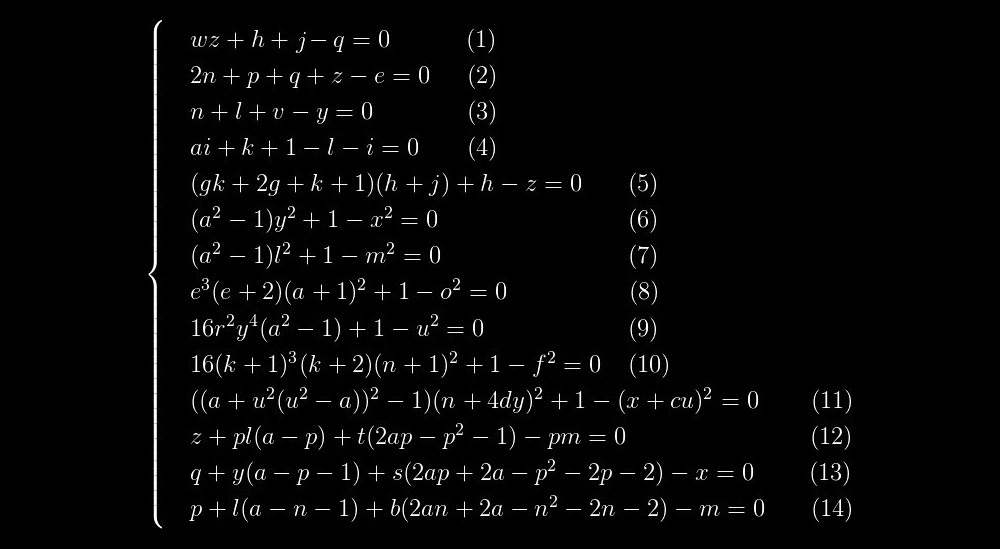
Если решить эту систему уравнений и прибавить 2 к найденному значению k, то мы получим простое число. Но мы можем пойти и другим путем. Взять некоторое простое число, вычесть из него 2, получив таким образом значение k, затем подставить это значение в систему и попытаться найти значения остальных переменных относительно него. Именно этим путем мы и пойдем — попытаемся найти хоть одно решение данного полинома.
На все переменные накладывается два строгих ограничения, они должны быть целыми и не могут быть отрицательными. Если мы примем k=0, то первое простое число, которое мы сможем получить — это 2. Это и будет нашей отправной точкой. После подстановки этого значения в систему уравнений она примет следующий вид:
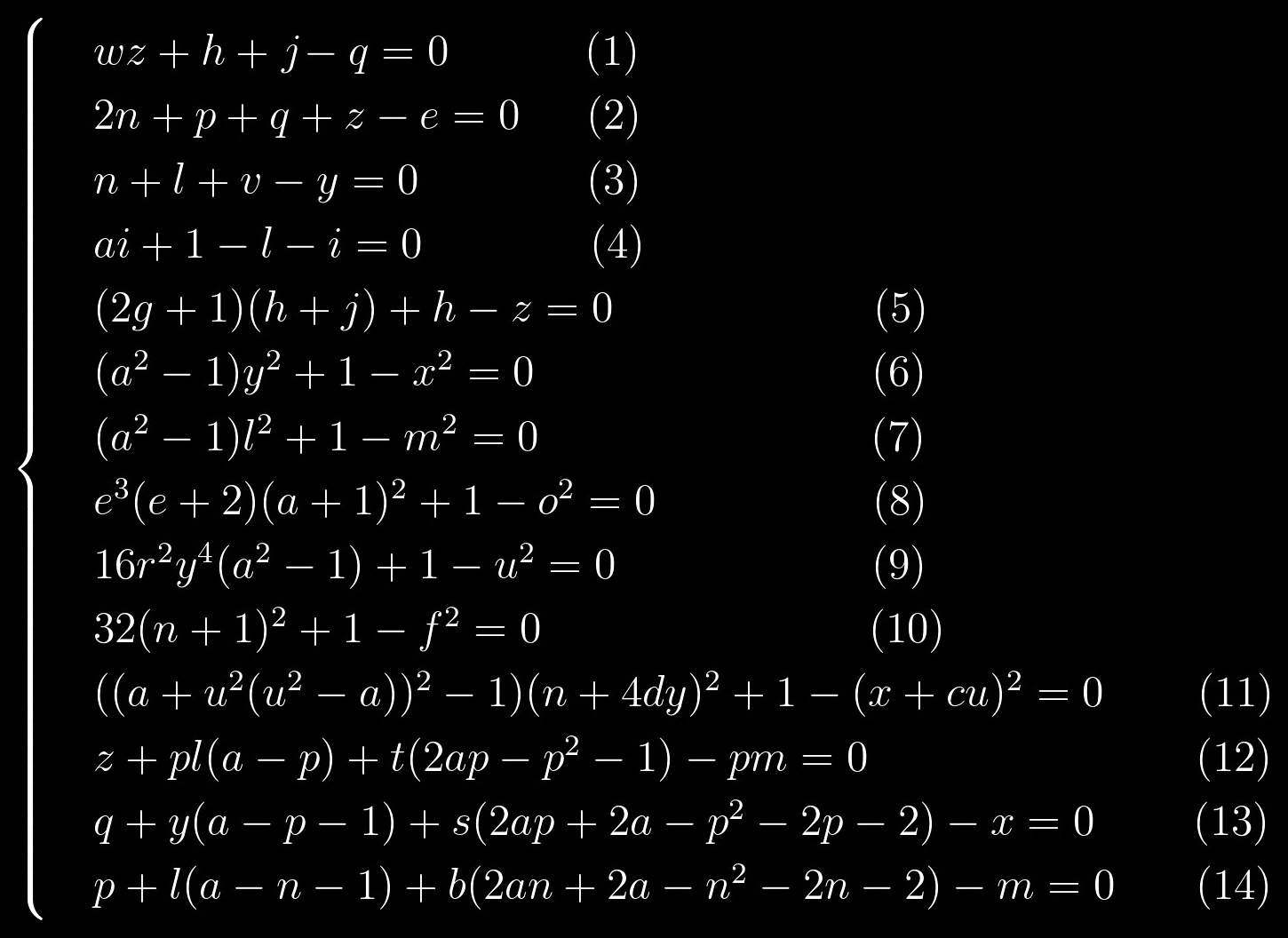
Уравнения (1)-(5) — это линейные уравнения, т.е. степени всех переменных равны 1. Уравнения (6)-(11) имеют очень схожую структуру. Ну и, наконец, уравнения (12)-(14) тоже выделяются в отдельную группу, причем уравнения (13) и (14) похожи друг на друга, как две капли воды.
Мы можем избавляться от переменных, или понижать степень, но до нас этим уже занимались. Уменьшение количества переменных приводит к сильному росту степеней других переменных, а уменьшение степеней переменных возможно только через увеличение их количества. Так что попробуем решить эту систему именно в таком виде.
Уравнения (6)-(11) являются модификациями уравнения Пелля:
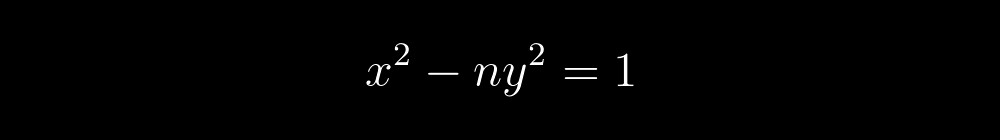
В самом деле, если переписать их вот так:
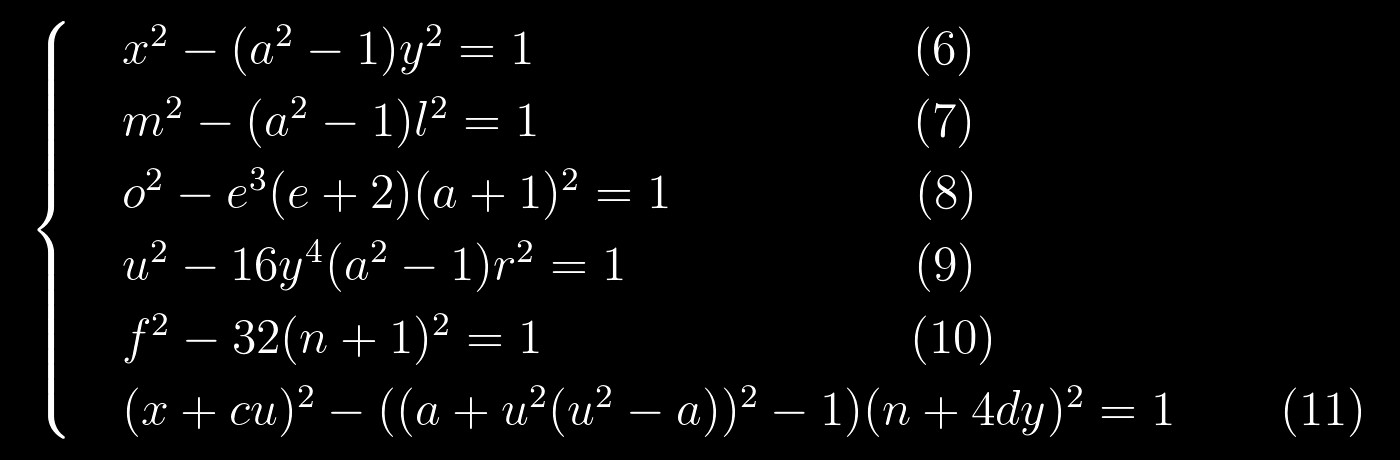
то сходство становится очевидным. Это очень обнадеживающе, так как решать уравнения Пелля мы умеем довольно неплохо. Мы можем попробовать решать эту систему примерно так: сначала решаем какое-нибудь одно уравнение, его решения подставляем в другое, которое тоже решаем и так далее, до самого конца. Звучит довольно просто, но не мешало бы нарисовать что-то вроде графа подстановок, чтобы хоть примерно знать, в каком порядке решать уравнения:
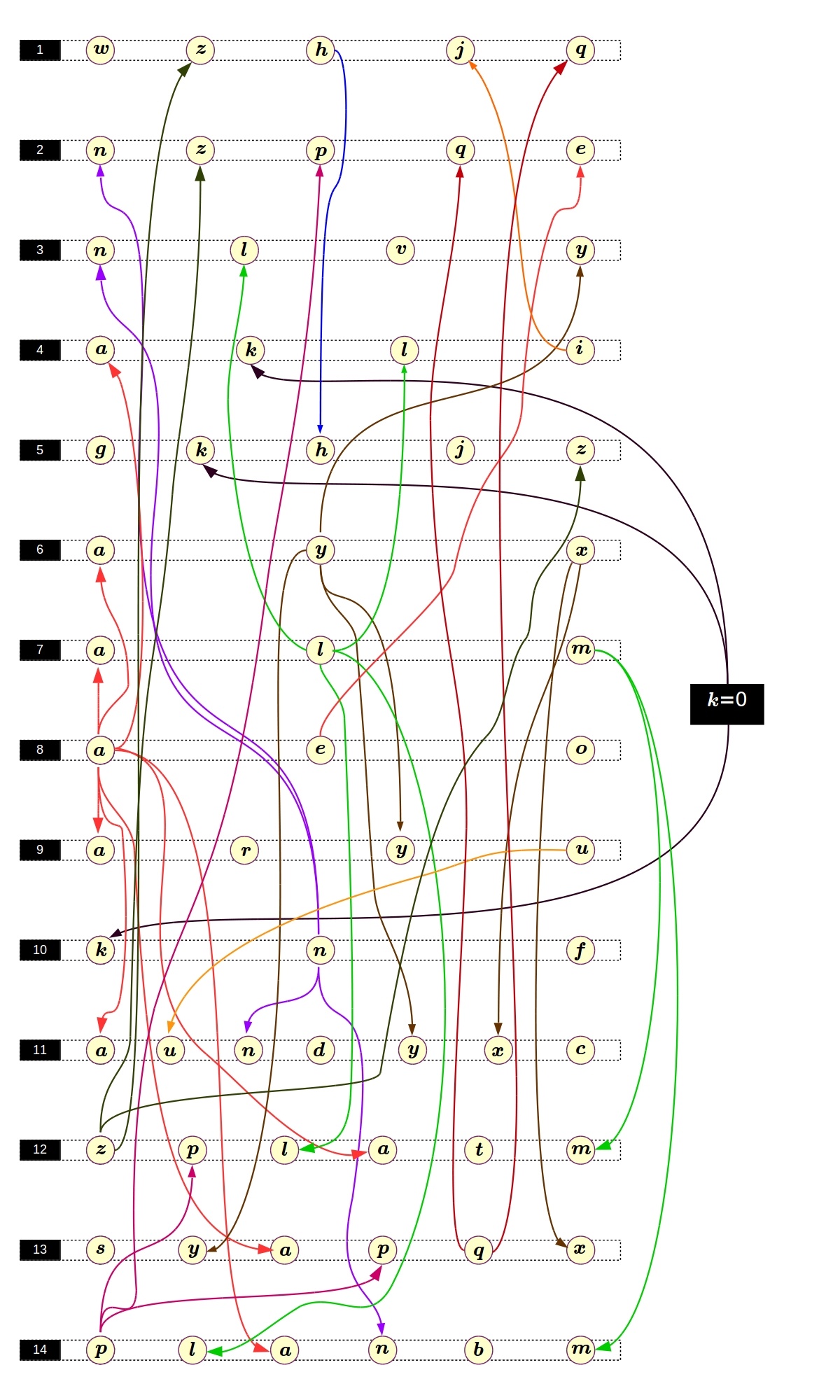
Вроде, все просто.
Удар по стене
Мы начнем с уравнений Пелля. Для их решения напишем небольшой скрипт:
from decimal import *
getcontext().prec = 50
def peq_dec(N):
n = Decimal(N).sqrt()
a = int(n)
x = n - a
p0, q0 = 1, 0
p1, q1 = int(a), 1
while True:
a = int(1/x)
x = 1/x - a
p_i = a*p1 + p0
q_i = a*q1 + q0
if p_i**2 - N*q_i**2 == 1:
return p_i, q_i
break
p0, q0 = p1, q1
p1, q1 = p_i, q_iБлагодаря ему мы можем сразу найти решение уравнения (10) n = 2, f = 17. Однако, прежде чем двигаться дальше, мы должны кое-что знать об уравнении Пелля.
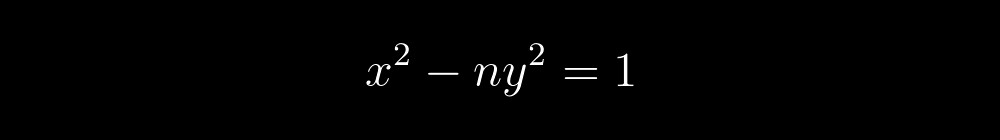
Начнем с того, что n не может быть полным квадратом. К тому же у любого уравнения Пелля существует бесконечное количество решений, среди которых всегда есть тривиальное: x = 1 и y = 0. Каждое последующее решение может быть получено на основе предыдущих, по следующей рекуррентной формуле:
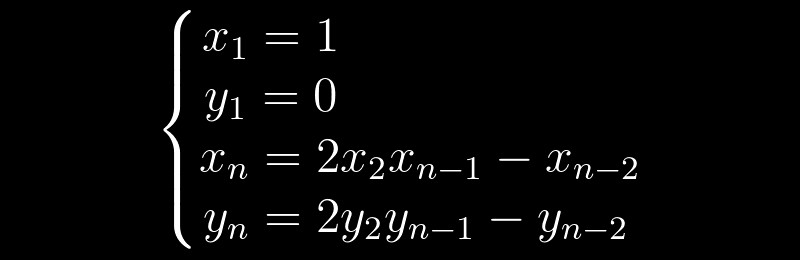
Получается, что нам достаточно найти минимальное нетривиальное решение, а все остальные мы можем получить, пользуясь простым алгоритмом. Например, для n = 2 мы можем легко найти такое решение, это x = 3 и y = 2, тогда последующие решения будут выглядеть так:
17, 12
99, 70
577, 408
3363, 2378
19601, 13860
114243, 80782
665857, 470832
3880899, 2744210
22619537, 15994428
131836323, 93222358
768398401, 543339720
4478554083, 3166815962
26102926097, 18457556052
152139002499, 107578520350
886731088897, 627013566048Стоит ли продолжать дальнейшее решение? Конечно, стоит, но… мы можем попытаться предугадать, что нас ждет впереди.
Давайте пока просто представим, что мы решаем систему уравнений из трех уравнений Пелля следующего вида:
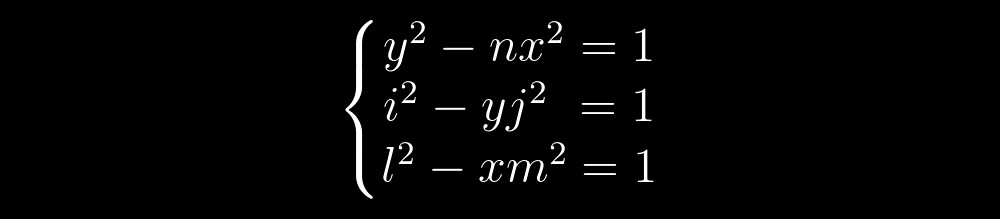
Решением любого уравнения Пелля являются точки гиперболы с целыми координатами. Тогда, мы можем вообразить решение первых двух уравнений примерно так:
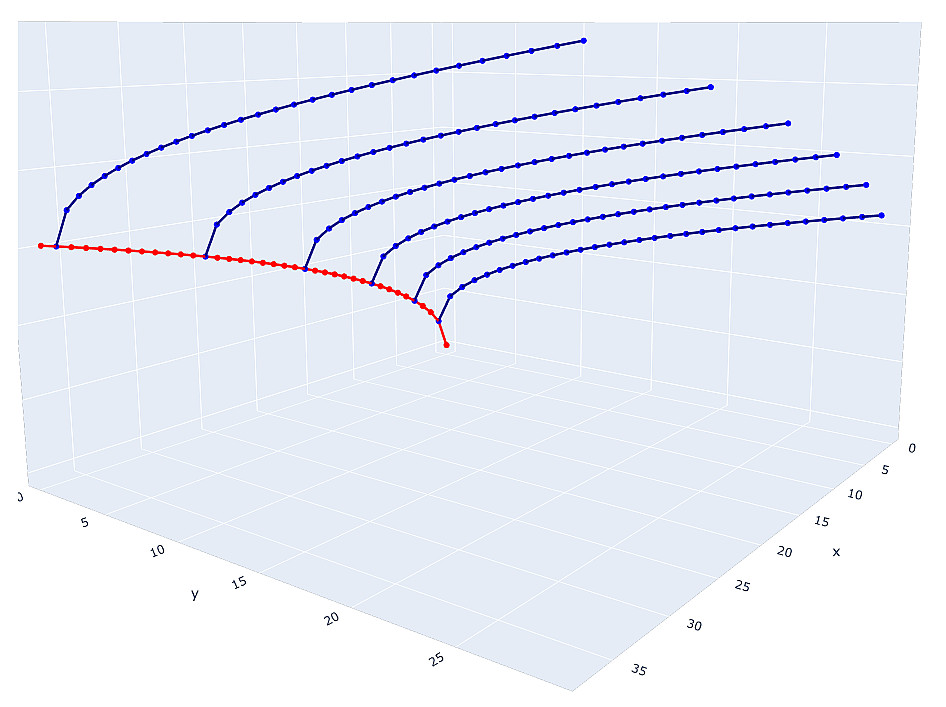
Решением первого уравнения являются целочисленные точки красной гиперболы, но координата y, каждой такой такой точки присутствует во втором уравнении и может порождать любую гиперболу синего цвета, целочисленные точки которой будут являться решением второго уравнения.
Даже этого схематического графика достаточно, чтобы понять, что мы имеем дело с очень большим множеством потенциальных кандидатов на решение системы. Почему кандидатов? Потому что некоторые целочисленные точки гиперболы обязательно будут полными квадратами, т.е. неподходящими решениями. А если представить, что на каждую переменную в системе накладываются какие-то дополнительные условия, то поиск кандидатов на решение станет чрезвычайно трудным. А речь пока идет только системе из трех уравнений.
Но давайте вернемся к нашей «формуле» простых чисел. Что нас может ждать впереди?
Рано или поздно мы обнаружим, что параметр n в уравнении Пелля будет становиться катастрофически большим. Метод цепных дробей станет просто бесполезен. Мы обязательно попробуем что-нибудь еще, например перебор значений с просеиванием, как-нибудь обобщим весь этот процесс и придем к алгоритмам подобным квадратичному решету или решету числового поля. В конце концов мы остановимся на методе «чакравала», хотя и он будет испытывать некоторые трудности.
В определенный момент мы почувствуем некоторую уверенность в решении каждого отдельного уравнения системы. Но не всей системы. Мы постараемся применить какие-нибудь эвристические методы оптимизации, например, алгоритм отжига, или алгоритм муравья. Но и здесь мы потерпим неудачу. Для того, чтобы хоть как-то понять причины этих неудач, нам придется немного погрузиться в алгебраическую геометрию и топологию. Постепенно мы получим какое-то представление о «кристаллизуемой субстанции». Сможем отдаленно представить структуру гиперповерхности, на которую выпускаем муравьев.
Опираясь на эти представления мы постараемся улучшить наши алгоритмы. Чтобы сделать это, мы будем брать самые лучшие достижения из многих разделов математики. Постепенно, в алгоритмах будет меньше случайности, но избавиться от нее все равно не получится. Что произойдет потом? Мы вдруг обнаружим, что множество подходящих кандидатов на истинное решение в некоторых местах является парадоксально плотным. Каждая такая плотность будет дарить надежду на то, что где-то в ее центре и спрятан заветный ответ. Муравьям такие плотности будут «казаться» чем-то вроде перевернутой гиперворонки. Мы будем стараться «бить» по их центрам и максимумам. Но что произойдет потом?
Что за стеной?
Наверное, не знаю как, но мы решим это уравнение. Может быть, нам помогут квантовые или (!) кварковые компьютеры. Но и это не станет дырой в стене. Наверное, дальше нас будут ждать гаусовы простые числа и еще более сложное уравнение, которое будет представлять их множество. Потом, возможно, среди других гиперкомплексных чисел мы снова наткнемся на какое-то подобие «простого» поведения. Может это, в конце концов, и будет пределом, своеобразным горизонтом событий математической черной дыры.
Что может быть под этим горизонтом? Наверное, какая-то математическая сингулярность. Наверное, мы будем знать абсолютно все обо всех множествах, сможем решать любые уравнения и любые задачи. А может новых вопросов и задач больше вообще не будет?
Возникают именно такие мысли. Ну в самом деле, задайте любой вопрос о простых числах и благодаря данному уравнению вы можете получить на него ответ. Бесконечно ли количество простых чисел-близнецов? Решите данное уравнение, сделайте парочку алгебраических выкладок и получите ответ. Каких простых чисел больше, оканчивающихся на 1, 3, 7 или 9? Тот же самый алгоритм: пара-тройка выкладок и подстановка уравнения. Хотите быстро раскладывать числа на простые множители?..
В заключение
Впервые с этим уравнением я познакомился в 2008 году, к тому времени я уже сходил с ума по криптографии и теории чисел, в частности по схеме RSA и задаче факторизации. Конечно же, полином, генерирующий простые числа, показался мне очень интересной темой, но слишком сложной. Однако, все задачи, которые удавалось или не удавалось решить, так или иначе были связаны с диофантовыми уравнениями. Поэтому, уже в 2014 году я вновь обратился к этому полиному, решив просто исследовать все разделы математики подряд и искать то, что могло бы пригодиться в его решении. Конечно, ни о какой академической культуре всех моих трудов не может быть и речи — я никогда не вел систематических записей, никогда не агрегировал создаваемый код. Это просто мое хобби.
Мысль о написании этой статьи появилась после того, как я увидел фильм «Интерстеллар». Я не мог поверить в то, что черные дыры и гравитация могут быть представлены так чертовски захватывающе. Но, как оказалось, «не существующий» мир математики снабжал меня такими же впечатлениями постоянно. В этом мире тоже есть свой недоступный «дальний космос» и свои «элементарные частицы».
Этой статьей я хотел показать, что к любой, самой сложной, даже непосильной задаче можно хоть чуть-чуть подступиться. Таких задач очень много, и можно выбрать ту, что по душе и ближе всего к интересуемой сфере деятельности. Конечно, чрезмерная сложность и гарантированное поражение лишат малейшего желания в этом начинании. Но весь парадокс в том, что самые интересные путешествия и приключения, даже в «не существующем» мире математики, чаще всего, начинаются именно так.
Автор: Семён Лукашевский






