
Натолкнувшись на статью “Уничтожим монополию …”, автор, как человек пусть от EDA очень далёкий, но от природы любознательный, не поленился пройтись по ссылкам и невольно поймал себя на мысли, что одно из основных технических решений — использование рядов стандартных ячеек (standard cell layout) — выглядит довольно спорно.
Да, такое расположение интуитивно понятно, ведь мы пишем и читаем похожим образом, кроме того, технологически просто располагать ячейки именно рядами, так удобно стыковать шины VDD и GND. С другой стороны, при этом возникает непростая комбинаторная задача, требуется разрезать схему на линейные куски и расположить эти куски таким образом, чтобы (грубо) минимизировать общую длину соединений.
И конечно же возник вопрос, нет ли альтернативных решений, … вот что если …
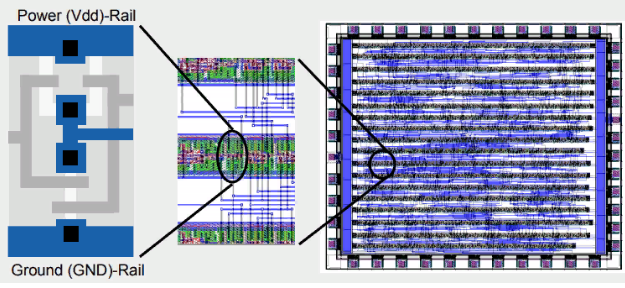
Фиг.1 типичные ряды стандартных ячеек (отсюда)
А что если
С точки зрения уменьшения общей длины связей было бы полезно расположить стандартные ячейки вдоль какой-то из заметающих кривых ex: Пеано или Гильберта.
Эти кривые состоят из массы разнообразных “закоулков”, наверняка есть конфигурация в которой связанные стандартные ячейки в среднем окажутся недалеко друг от друга.
Или это может служить нулевой итерацией для дальнейшей оптимизации.
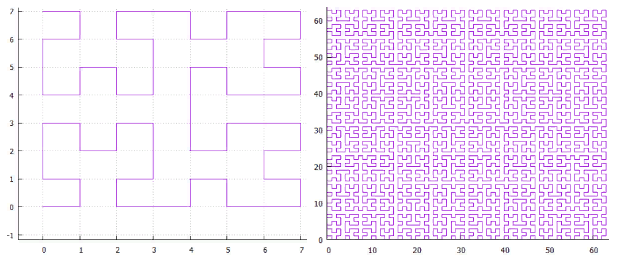
Фиг.2 Кривая Гильберта, поля 8X8 и 64X64
- Заметающие кривые самоподобны, что хорошо укладывается в общую концепцию.
- Они имеют высокую локальность т.е. точки, находящиеся где-то рядом на кривой скорее всего находятся недалеко и в пространстве.
- Содержат иерархически организованную сеть каналов.
- Для логической схемы можно подобрать подходящий квадрат или прямоугольник 1х2,2х1, в котором она размещается с избытком и «подвигать» ее вдоль заметающей кривой (см. Фиг.3) чтобы подобрать оптимальную геометрию, ведь это всего одна степень свободы с довольно дешевой функцией стоимости.
- Сохранится удобство стыковки шин (VDD/GND).
- …
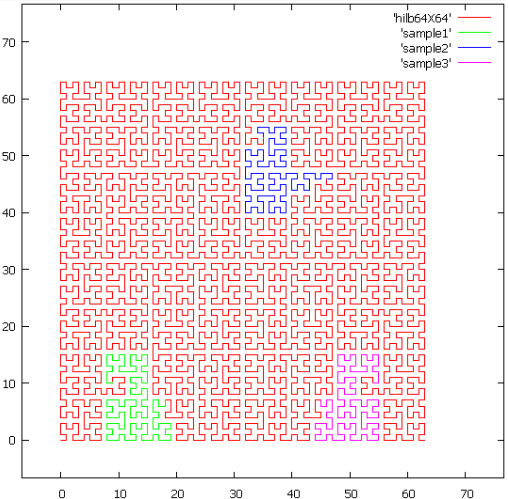
Фиг.3 Три куска кривой Гильберта с разными сдвигами.
Итак:
- экспериментировать будем с кривой Гильберта
- экспериментировать будем в квадрате 64X64 (Фиг.3)
- в элементарном шаге кривой может быть несколько стандартных ячеек и пробелов — сколько именно и в каком порядке — параметр эксперимента
- все элементарные шаги устроены одинаково
- элементарные шаги идут с нахлёстом т.е. если шаг начинается со стандартной ячейки, в конце его должен быть пробел, и наоборот
- все пробелы и стандартные ячейки имеют один размер — 1X1
- все ячейки сериализованы в каком-то порядке, этот порядок тоже является параметром
- еще один параметр — сдвиг от начала кривой (точки (0,0)), начиная с которого мы будем располагать стандартные ячейки в определенном порядке
- длины связей между стандартными ячейками считаются по L1 (манхэттенское расстояние)
- сумма длин всех связей и является искомой величиной, определив минимальную сумму мы и найдем оптимальное расположение
А в качестве подопытного кролика возьмём 8-разрядный сумматор. Он достаточно прост, но не тривиален. В нём достаточно много элементов и связей, чтобы почувствовать потенциальные плюсы и минусы. В тоже время их достаточно немного для того, чтобы можно было экспериментировать “на коленке”.
Сумматор
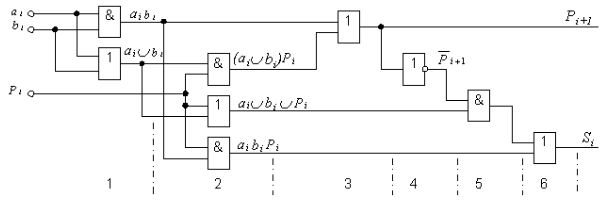
Фиг.4 принципиальная схема полного одноразрядного сумматора
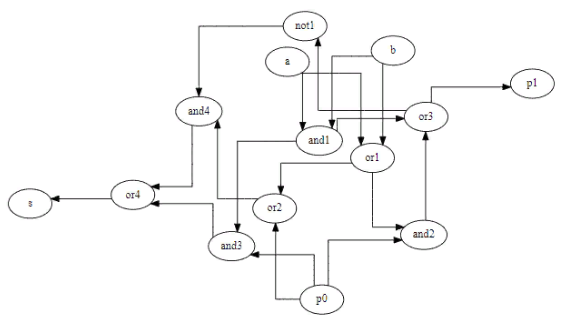
Фиг.5 Так видит это граф утилита Neato из graphwiz
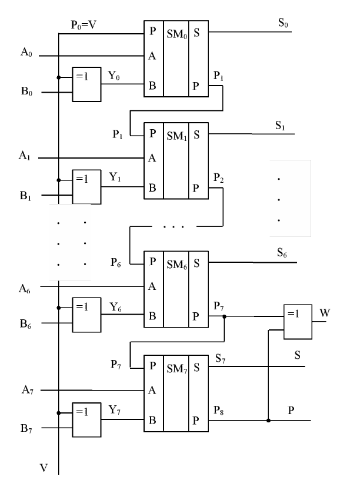
Фиг.6 8-разрядный знаковый сумматор, взято здесь
Но мы будем работать только с целыми числами, без флага ошибки W.
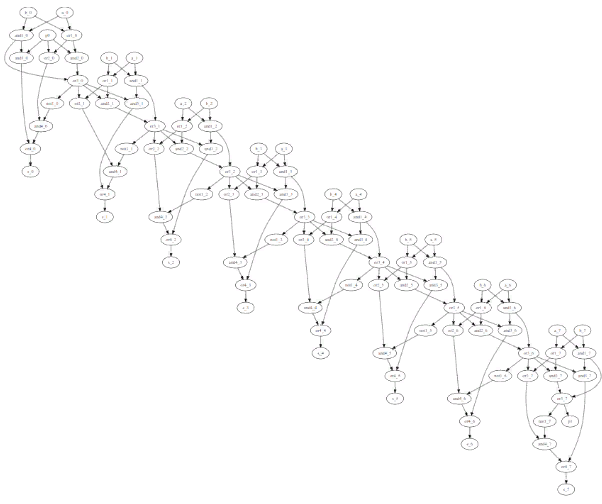
Фиг.7 Так 8-разрядный сумматор видит утилита dot из graphwiz.
Выглядит как танец маленьких лебедей.
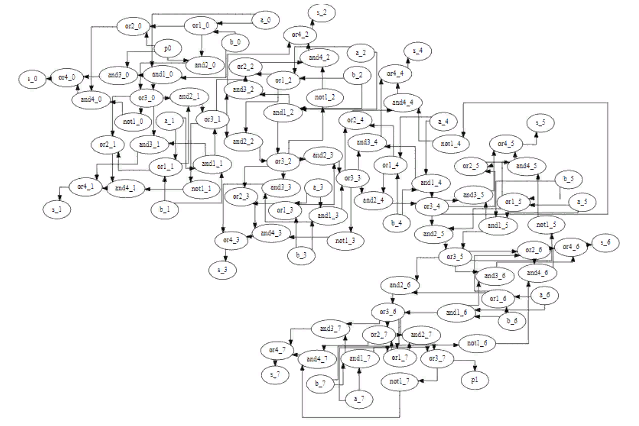
Фиг.8 тот же граф после оптимизации с помощью neato.
a_0;
a_1;
a_2;
a_3;
a_4;
a_5;
a_6;
a_7;
b_0;
b_1;
b_2;
b_3;
b_4;
b_5;
b_6;
b_7;
s_0;
s_1;
s_2;
s_3;
s_4;
s_5;
s_6;
s_7;
p0;
p1;
and1_0;
and1_1;
and1_2;
and1_3;
and1_4;
and1_5;
and1_6;
and1_7;
and2_0;
and2_1;
and2_2;
and2_3;
and2_4;
and2_5;
and2_6;
and2_7;
and3_0;
and3_1;
and3_2;
and3_3;
and3_4;
and3_5;
and3_6;
and3_7;
and4_0;
and4_1;
and4_2;
and4_3;
and4_4;
and4_5;
and4_6;
and4_7;
or1_0;
or1_1;
or1_2;
or1_3;
or1_4;
or1_5;
or1_6;
or1_7;
or2_0;
or2_1;
or2_2;
or2_3;
or2_4;
or2_5;
or2_6;
or2_7;
or3_0;
or3_1;
or3_2;
or3_3;
or3_4;
or3_5;
or3_6;
or3_7;
or4_0;
or4_1;
or4_2;
or4_3;
or4_4;
or4_5;
or4_6;
or4_7;
not1_0;
not1_1;
not1_2;
not1_3;
not1_4;
not1_5;
not1_6;
not1_7;
a_0 -> and1_0;
a_1 -> and1_1;
a_2 -> and1_2;
a_3 -> and1_3;
a_4 -> and1_4;
a_5 -> and1_5;
a_6 -> and1_6;
a_7 -> and1_7;
b_0 -> and1_0;
b_1 -> and1_1;
b_2 -> and1_2;
b_3 -> and1_3;
b_4 -> and1_4;
b_5 -> and1_5;
b_6 -> and1_6;
b_7 -> and1_7;
a_0 -> or1_0;
a_1 -> or1_1;
a_2 -> or1_2;
a_3 -> or1_3;
a_4 -> or1_4;
a_5 -> or1_5;
a_6 -> or1_6;
a_7 -> or1_7;
b_0 -> or1_0;
b_1 -> or1_1;
b_2 -> or1_2;
b_3 -> or1_3;
b_4 -> or1_4;
b_5 -> or1_5;
b_6 -> or1_6;
b_7 -> or1_7;
and1_0 -> or3_0;
and1_1 -> or3_1;
and1_2 -> or3_2;
and1_3 -> or3_3;
and1_4 -> or3_4;
and1_5 -> or3_5;
and1_6 -> or3_6;
and1_7 -> or3_7;
and1_0 -> and3_0;
and1_1 -> and3_1;
and1_2 -> and3_2;
and1_3 -> and3_3;
and1_4 -> and3_4;
and1_5 -> and3_5;
and1_6 -> and3_6;
and1_7 -> and3_7;
or1_0 -> and2_0;
or1_1 -> and2_1;
or1_2 -> and2_2;
or1_3 -> and2_3;
or1_4 -> and2_4;
or1_5 -> and2_5;
or1_6 -> and2_6;
or1_7 -> and2_7;
or1_0 -> or2_0;
or1_1 -> or2_1;
or1_2 -> or2_2;
or1_3 -> or2_3;
or1_4 -> or2_4;
or1_5 -> or2_5;
or1_6 -> or2_6;
or1_7 -> or2_7;
and2_0 -> or3_0;
and2_1 -> or3_1;
and2_2 -> or3_2;
and2_3 -> or3_3;
and2_4 -> or3_4;
and2_5 -> or3_5;
and2_6 -> or3_6;
and2_7 -> or3_7;
or2_0 -> and4_0;
or2_1 -> and4_1;
or2_2 -> and4_2;
or2_3 -> and4_3;
or2_4 -> and4_4;
or2_5 -> and4_5;
or2_6 -> and4_6;
or2_7 -> and4_7;
and3_0 -> or4_0;
and3_1 -> or4_1;
and3_2 -> or4_2;
and3_3 -> or4_3;
and3_4 -> or4_4;
and3_5 -> or4_5;
and3_6 -> or4_6;
and3_7 -> or4_7;
or3_0 -> not1_0;
or3_1 -> not1_1;
or3_2 -> not1_2;
or3_3 -> not1_3;
or3_4 -> not1_4;
or3_5 -> not1_5;
or3_6 -> not1_6;
or3_7 -> not1_7;
not1_0 -> and4_0;
not1_1 -> and4_1;
not1_2 -> and4_2;
not1_3 -> and4_3;
not1_4 -> and4_4;
not1_5 -> and4_5;
not1_6 -> and4_6;
not1_7 -> and4_7;
and4_0 -> or4_0;
and4_1 -> or4_1;
and4_2 -> or4_2;
and4_3 -> or4_3;
and4_4 -> or4_4;
and4_5 -> or4_5;
and4_6 -> or4_6;
and4_7 -> or4_7;
or4_0 -> s_0;
or4_1 -> s_1;
or4_2 -> s_2;
or4_3 -> s_3;
or4_4 -> s_4;
or4_5 -> s_5;
or4_6 -> s_6;
or4_7 -> s_7;
p0 -> and2_0;
p0 -> or2_0;
p0 -> and3_0;
or3_0 -> and2_1;
or3_0 -> or2_1;
or3_0 -> and3_1;
or3_1 -> and2_2;
or3_1 -> or2_2;
or3_1 -> and3_2;
or3_2 -> and2_3;
or3_2 -> or2_3;
or3_2 -> and3_3;
or3_3 -> and2_4;
or3_3 -> or2_4;
or3_3 -> and3_4;
or3_4 -> and2_5;
or3_4 -> or2_5;
or3_4 -> and3_5;
or3_5 -> and2_6;
or3_5 -> or2_6;
or3_5 -> and3_6;
or3_6 -> and2_7;
or3_6 -> or2_7;
or3_6 -> and3_7;
or3_7 -> p1;
}
Эксперимент 1
- элементарный шаг кривой Гильберта — (пропуск, ячейка, ячейка, пропуск)
- вершины графа (элементарные ячейки) отсортированы по алфавиту
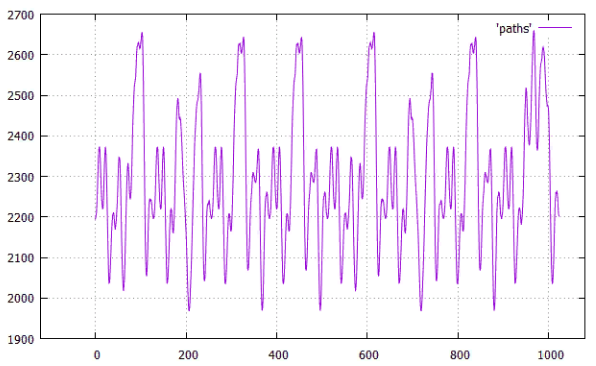
Фиг.9 по X — сдвиг от начала, по Y — длина всех путей
Минимальное расстояние (первое из) при сдвиге 207 (Общая длина всех связей — 1968), посмотрим как выглядит это оптимальное расположение.
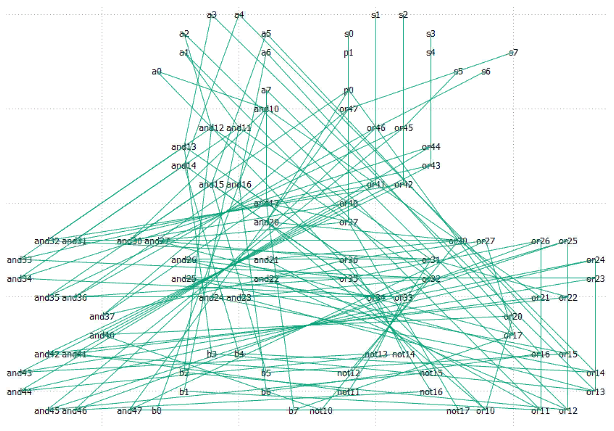
Фиг.10 оптимальный граф для сдвига 207, выглядит не очень красиво.
Эксперимент 2
- элементарный шаг кривой Гильберта — (пропуск, ячейка, ячейка, пропуск)
- вершины графа (элементарные ячейки) в естественном порядке (как пришло в описании графа, см. описание графа выше) -
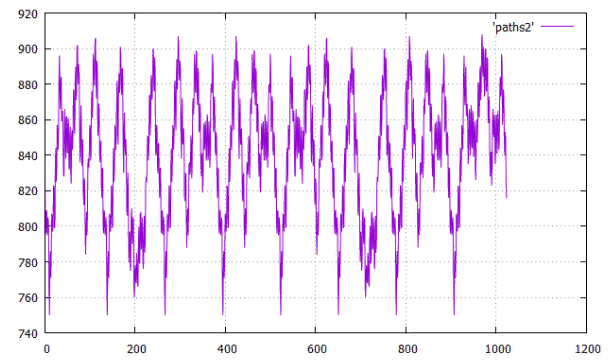
Фиг.11 по X — сдвиг от начала, по Y — длина всех путей

Фиг.12 оптимальный граф для сдвига 11 длина 750
Эксперимент 3
- элементарный шаг кривой Гильберта — (пропуск, ячейка, ячейка, пропуск)
- порядок вершин определён обходом графа в ширину, вершины без ссылок в начале списка, выходные — в конце
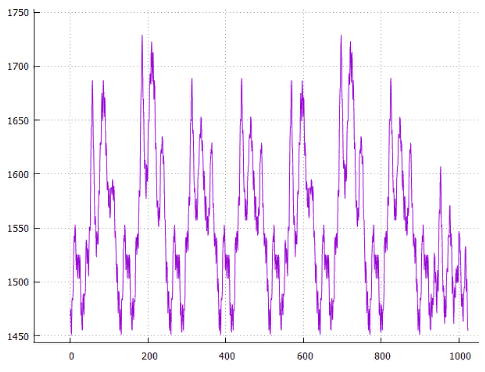
Фиг.13 по X — сдвиг от начала, по Y — длина всех путей
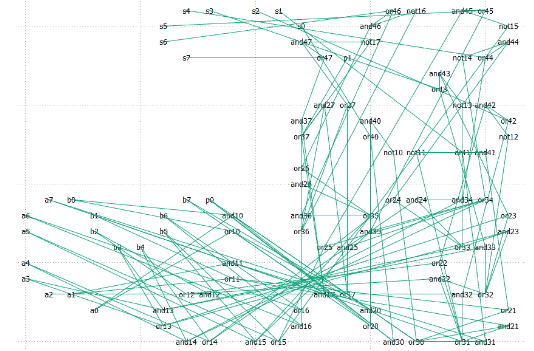
Фиг.14 Оптимальное расположение — сдвиг 3, общая длина 1451
Расположить все input вершины в начале, а output — в конце было не очень хорошей
идеей.
Эксперимент 4
- элементарный шаг кривой Гильберта — (пропуск, ячейка, ячейка) Sic!
- порядок вершин естественный, как в эксперименте 2
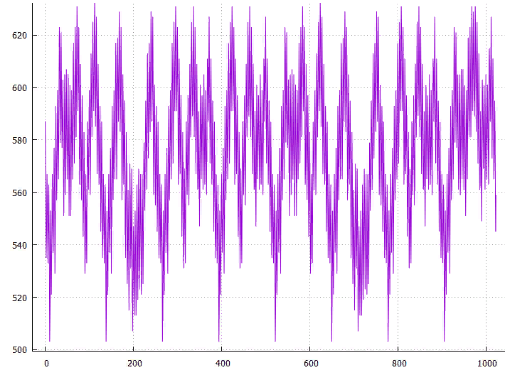
Фиг.15 по X — сдвиг от начала, по Y — длина всех путей

Фиг.16 Оптимальное расположение — сдвиг 10, общая длина 503
Эксперимент 5
С IO надо что-то делать, определим их в пост-процессинге, т.е. для каждого сдвига
построим расположение без IO вершин, потом построим поглощающий экстент-рамку вокруг графа, нанесем IO вершины на ближайшую незанятую точку рамки и посчитаем финальную длину
- элементарный шаг кривой Гильберта — (пропуск, ячейка, ячейка)
- порядок вершин определяется просмотром в ширину, но без IO вершин
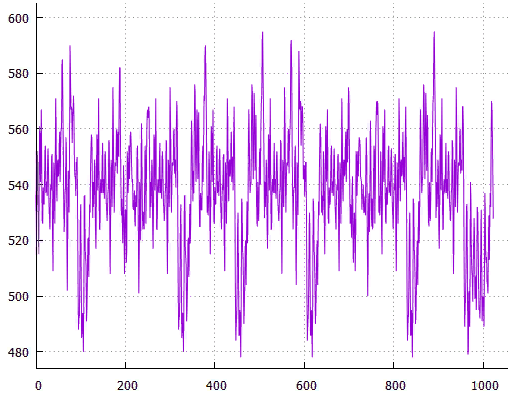
Фиг.17 по X — сдвиг от начала, по Y — длина всех путей
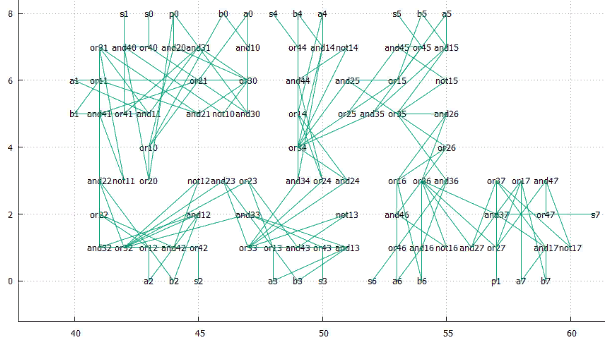
Фиг.18 Оптимальное расположение — сдвиг 607, общая длина 484, средняя 3.33793
Выглядит неплохо, а что если оптимизировать не общую длину путей, а её сумму с площадью занятого прямоугольника. У них размерность разная, поэтому будем считать, что подсчитываем не длину пути, а площадь под путями.
Эксперимент 6
Параметры те же что и в эксперименте 5, оптимизируем площадь.
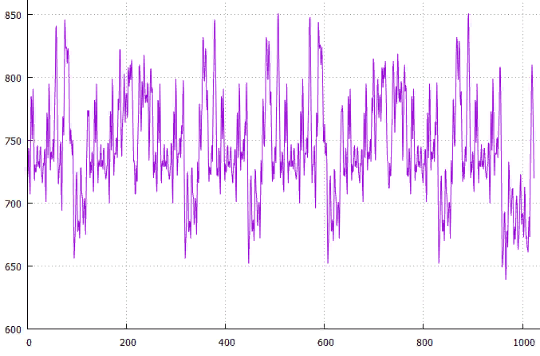
Фиг.19 по X — сдвиг от начала, по Y — длина всех путей
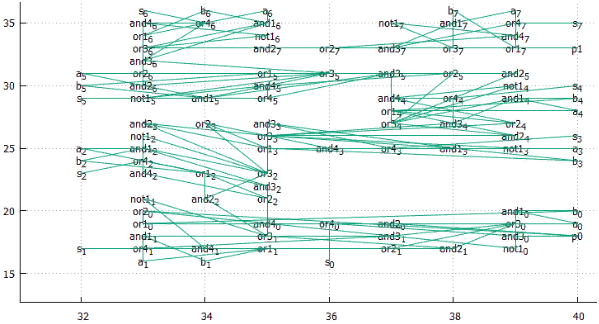
Фиг.20 Оптимальное расположение — сдвиг 966, общая длина 639, средняя 3.30345
Прямоугольник получился довольно вытянутым. А что если учитывать не площадь прямоугольника, а квадрат гипотенузы, подталкивая к более квадратным формам?
Эксперимент 7
Параметры те же что и в эксперименте 5, оптимизируем квадрат гипотенузы.
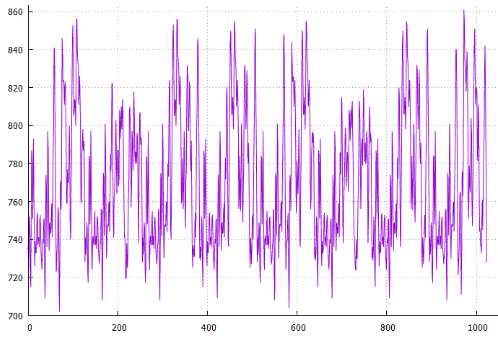
Фиг.21 по X — сдвиг от начала, по Y — длина всех путей
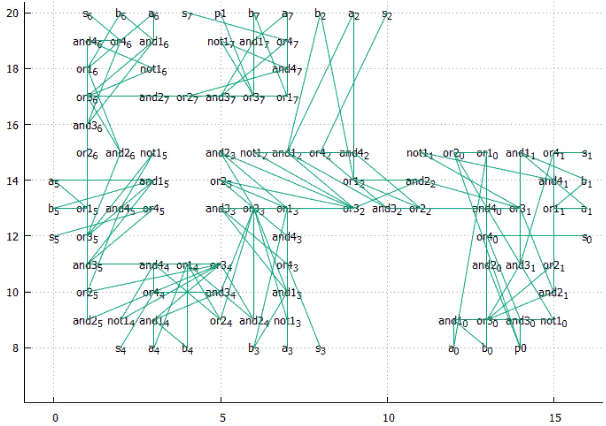
Фиг.22 Оптимальное расположение — сдвиг 70, общая длина 702, средняя 3.46207
Выводы
Предварительный “выбор редакции” — эксперимент 6.
Было бы неплохо упорядочить IO-вершины, но для этого нужна подсказка со стороны,
где именно (направление) следует расположить данный класс вершин.
Но прежде хотелось бы услышать мнение специалистов.
P.S.: спасибо YuriPanchul и andy_p за отсутствие рефлекторной отрицательной реакции.
Автор: zzeng




