Фраза в кавычках — название группы VK со следующим описанием:
Одна и та же фотография каждый день вручную сохраняется на компьютер и снова заливается, постепенно теряя в качестве.
Слева исходная картинка, загруженная 7 июня 2012, справа — какая она сейчас.
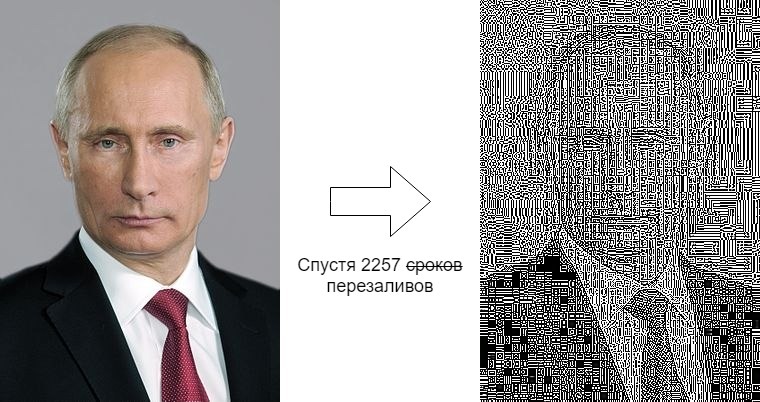
Такая разница очень подозрительна. Попробуем разобраться, что происходило в течение этих 7 лет.
Почему и на каком этапе JPEG сжимает с потерями
Рассмотрим сильно упрощенную схему кодирования и декодирования JPEG. Показаны только те операции, которые иллюстрируют основные принципы алгоритма JPEG.
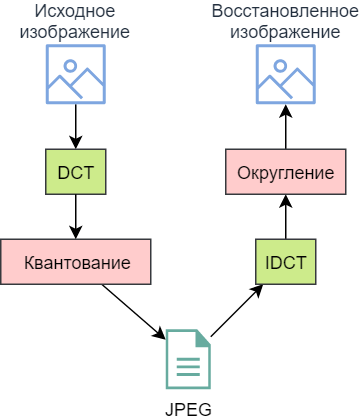
Итак, 4 операции:
- DCT — дискретное косинусное преобразование.
- Квантование — округление каждого значения до ближайшей величины, кратной шагу квантования: y = [x/h]*h, где h — шаг.
- IDCT — обратное дискретное косинусное преобразование.
- Округление — обычное округление. Этот этап можно было не показывать на схеме, так как он очевиден. Но далее будет продемонстрирована его важность.
Зеленым цветом выделены операции, сохраняющие всю информацию (не принимая во внимание потери при работе с числами с плавающей запятой), розовым — теряющими. То есть, потери и артефакты появляются не из-за косинусного преобразования, а из-за простого квантования. В статье не будет рассматриваться важный этап — кодирование Хаффмана, так как оно выполняется без потерь.
Рассмотрим эти шаги подробнее.
DCT
Так как существует несколько вариаций DCT, то на всякий случай уточню, что JPEG использует DCT второго типа с нормализацией. При кодировании каждое изображение разбивается на квадраты 8x8 (для каждого канала). Каждый такой квадрат можно представить в виде 64-мерного вектора. Косинусное преобразование заключается в нахождении координат этого вектора в другом ортонормированном базисе. Сложно визуализировать 64-мерное пространство, поэтому далее будут приведены 2-мерные аналогии. Можете представлять, что картинка разбивается на блоки 2x1. На графиках, которые будут продемонстрированы далее, оси x соответствуют значения первого пикселя блока, оси y — второго.
Продолжая аналогию на конкретном примере, допустим, что значения двух пикселей из исходного изображения — 3 и 4. Нарисуем вектор (3, 4) в исходном базисе, как показано на рисунке ниже. Исходный базис отмечен синим цветом. Координаты вектора в некотором новом базисе — (4.8, 1.4).
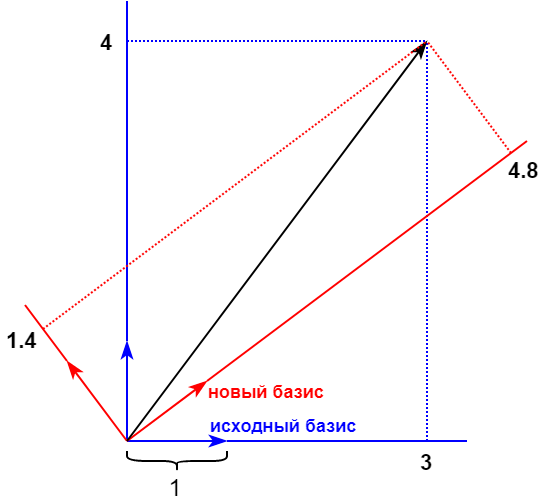
В рассмотренном примере новый базис был выбран случайно. DCT же предлагает вполне конкретный 64-мерный фиксированный базис. Обоснование того, почему в JPEG используется именно он, очень интересно, и описывалось мной в другой статье. Затронем лишь суть. В целом значения всех пикселей равноценны. Но если преобразовать их с помощью DCT, то из получившихся 64 координат в новом базисе (называемых коэффициентами DCT-преобразования) мы можем смело обнулить или грубо округлить их некоторую часть, получив минимальные потери. Это возможно благодаря особенностям сжимаемых изображений.
Квантование
В файле нельзя сохранить дробные значения. Поэтому, в зависимости от шага квантования, значения 4.8, 1.4 будут сохранены так:
- при шаге 1 (самый щадящий вариант): 5 и 1,
- при шаге 2: 4 и 2,
- при шаге 3: 6 и 0.
Обычно шаг выбирается разный для каждого значения. В JPEG-файле есть как минимум один массив, называемый таблицей квантования, хранящий 64 шага квантования. Эта таблица зависит от качества сжатия, задаваемое в любом графическом редакторе.
IDCT
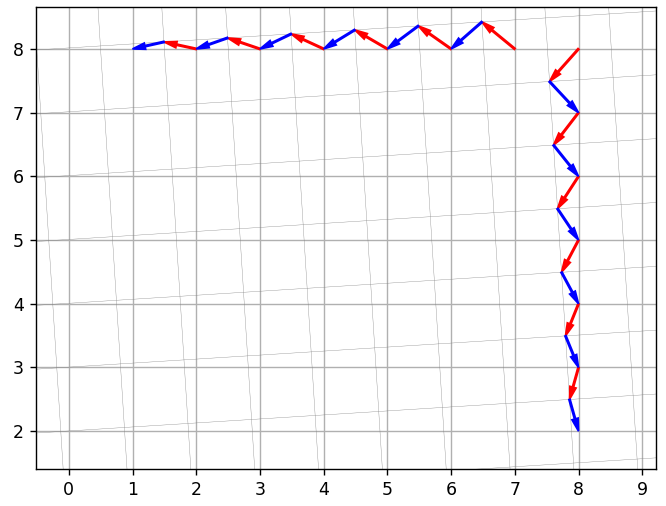
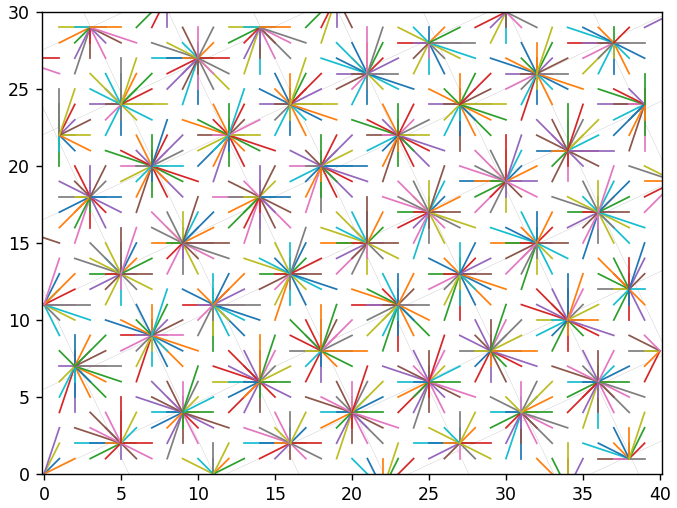
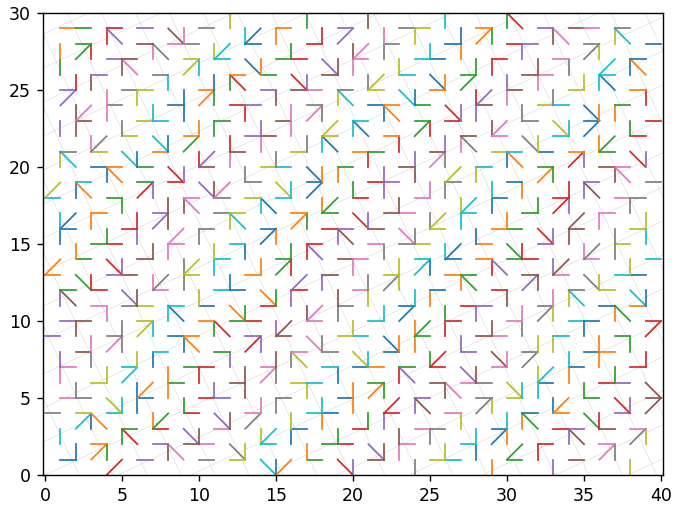
То же самое, что DCT, но с транспонированным базисом. Математически, x = IDCT(DCT(x)), поэтому если бы не было квантования, то можно было бы восстанавливать без потерь. Но не было бы и сжатия. Из-за использования квантования исходный вектор не всегда можно вычислить точно. На следующем рисунке представлены 2 примера с точным и неточным восстановлением. Наклонной сетке соответствует новый базис, прямой — исходный.
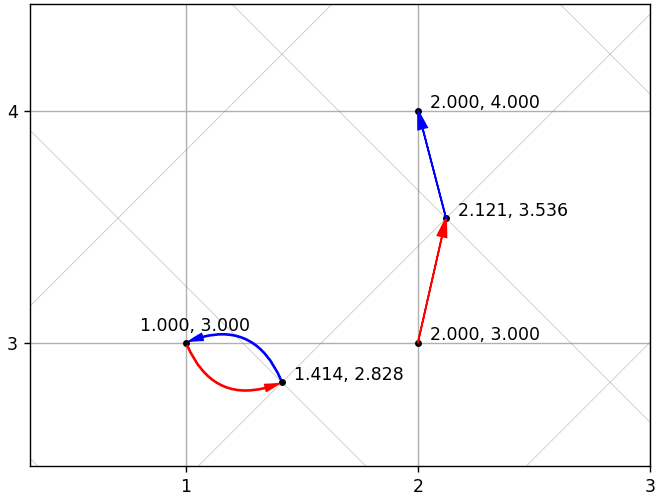
Возникает очевидный вопрос: может ли последовательность перекодирований привести к вектору, сильно отличающегося от исходного? Может.
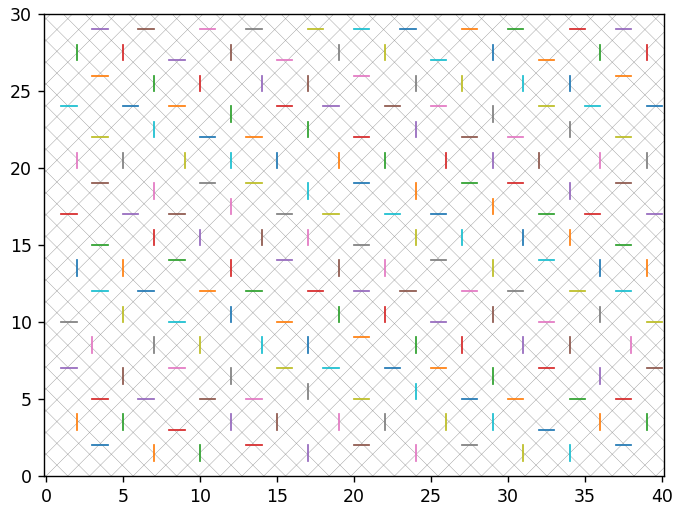
Интересно было бы перебрать все целочисленные векторы и посмотреть, к чему приведет их перекодирование. Для уменьшения информационного шума, уберем сетку исходного базиса и будем напрямую соединять отрезками исходные и восстановленные векторы (без промежуточного шага). Сначала рассмотрим шаг квантования равный 1 для всех координат. Новый базис на следующем рисунке повернут на 45 градусов и для него имеем 17.1% неточных восстановлений. Цвета отрезков ничего не означают, но они будут полезны для предотвращения их визуального слияния.
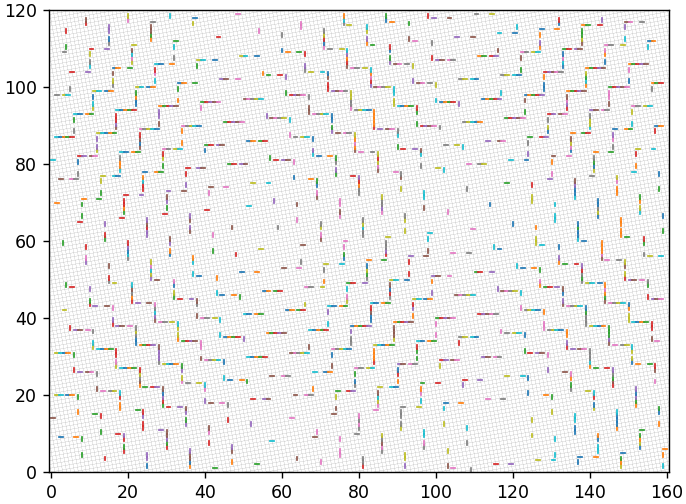
Этот базис — на 10.3 градусов с 7.4% неточных восстановлений:
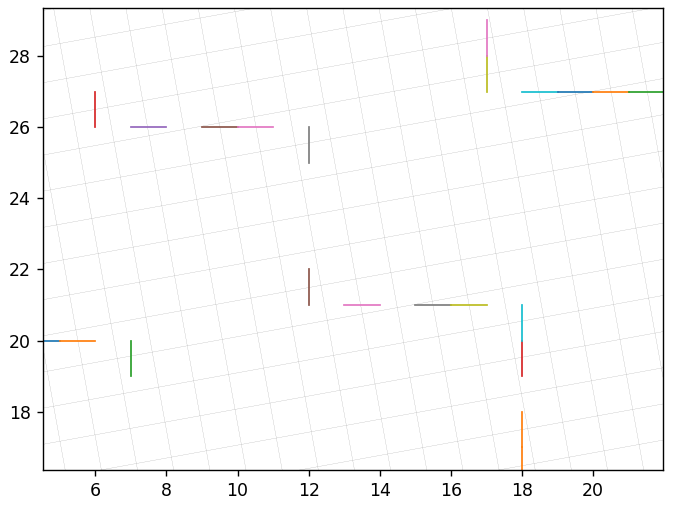
Вблизи:
А этот — на 10.4 с 6.4%:
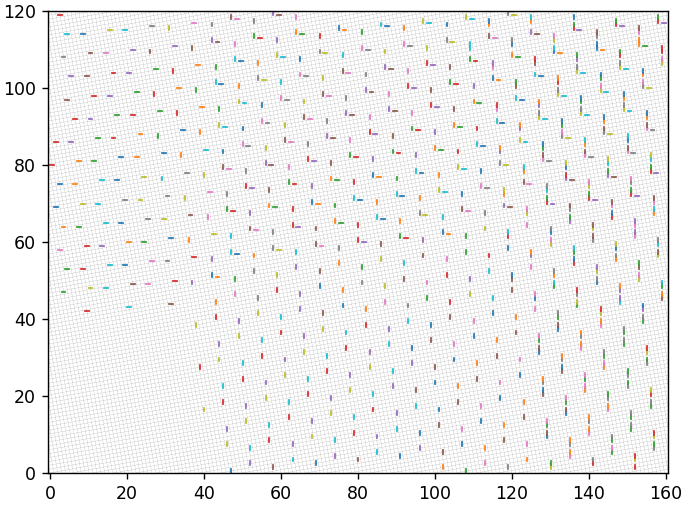
19 градусов с 12.5%:
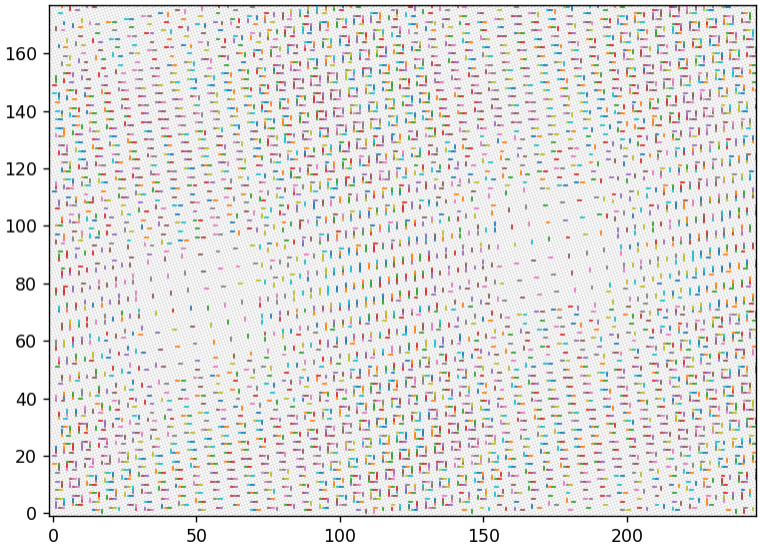
А вот если задать шаг квантования больше 1, то восстановленные векторы начинают явно концентрироваться близко к узлам сетки. Это шаг 5:
Это 2:
Если изображение перекодировать несколько раз, но с одинаковым шагом, то почти ничего не произойдет по сравнению с однократным перекодированием. Значения как бы «застревают» в узлах сетки и уже не могут «выпрыгнуть» оттуда в другие узлы. Если же шаг разный, то вектор будет «скакать» из одного узла сетки в другой. Это может завести его как угодно далеко. На следующем рисунке показан результат 4 перекодирований с шагами 1, 2, 3, 4. Можно разглядеть крупную сетку с шагом 12. Это значение — наименьшее общее кратное 1, 2, 3, 4.
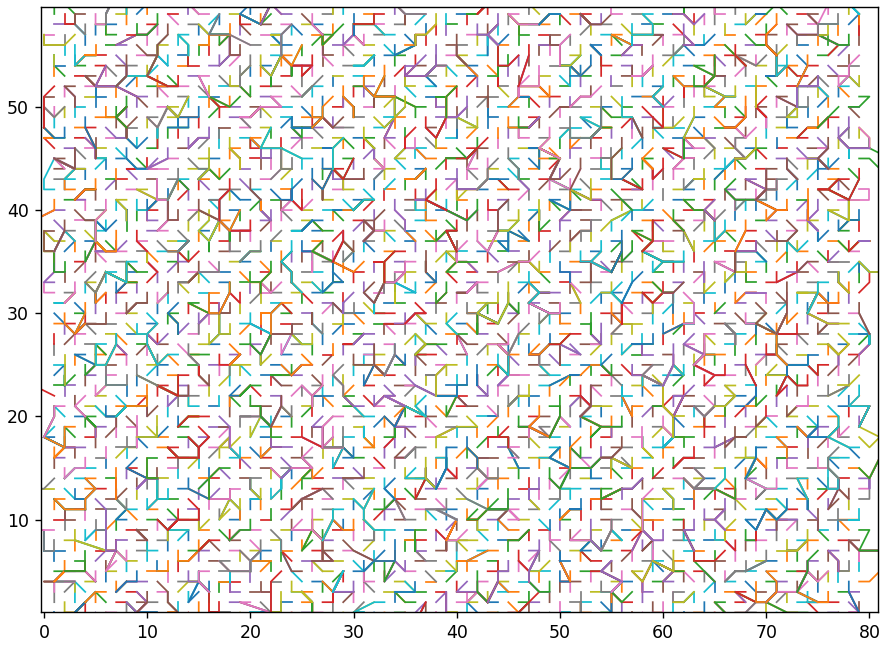
А на этом — с шагами от 1 до 7. Визуализация показана только для части исходных векторов, чтобы улучшить наглядность.
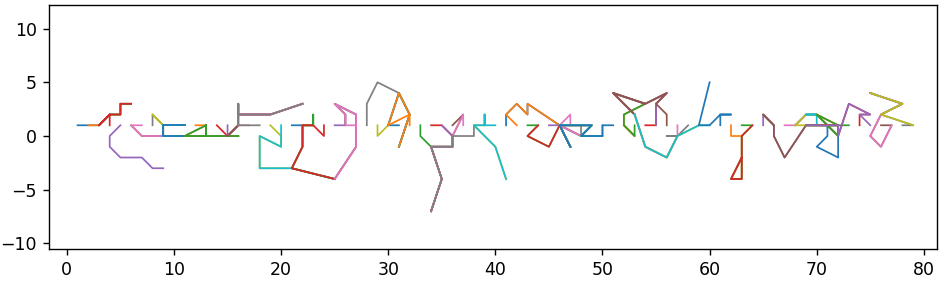
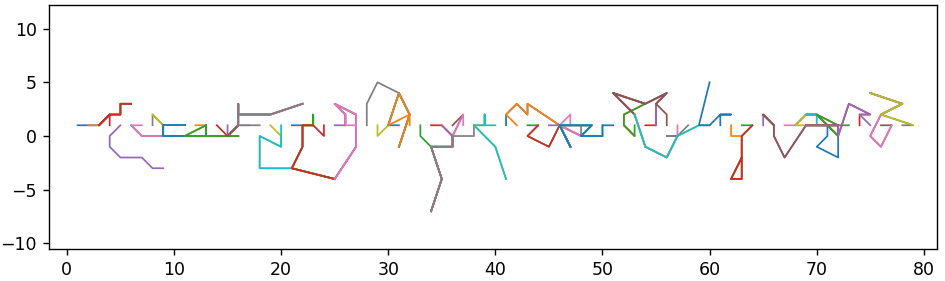
Округление
А зачем округлять значения после IDCT? Ведь если избавиться от этого этапа, то восстанавливаемое изображение будет представлено дробными значениями, и мы ничего не потеряем при повторном кодировании. С математической точки зрения, мы будем просто переходить от одного базиса к другому без потерь. Здесь необходимо упомянуть о преобразовании цветовых пространств. Хотя JPEG не регламентирует цветовое пространство и позволяет сохранять непосредственно в исходном RGB, но в подавляющем количестве случаев используется предварительная конвертация в YCbCr. Особенности глаза и все такое. А такая конвертация тоже приводит к потерям.
Предположим, мы получили JPEG-файл, сжатый с максимальным качеством, то есть с шагом квантования 1 для всех коэффициентов. Мы не знаем, какой кодек был использован, но обычно кодеки выполняют округление после преобразования RGB -> YCbCr. Так как качество максимально, то после IDCT мы получим дробные, но довольно близкие значения к исходным в пространстве YCbCr. Если округлим, то большинство из них восстановятся в точности.
Но если не округлим, то из-за таких небольших отличий преобразование YCbCr -> RGB может еще больше отдалить их от исходных значений. При последующих перекодированиях разрыв будет увеличиваться все больше. Чтобы хоть как-то визуализировать этот процесс, воспользуемся методом главных компонент для проецирования 64-мерных векторов на плоскость. Тогда для 1000 перекодирований получим примерно такую последовательность изменений:
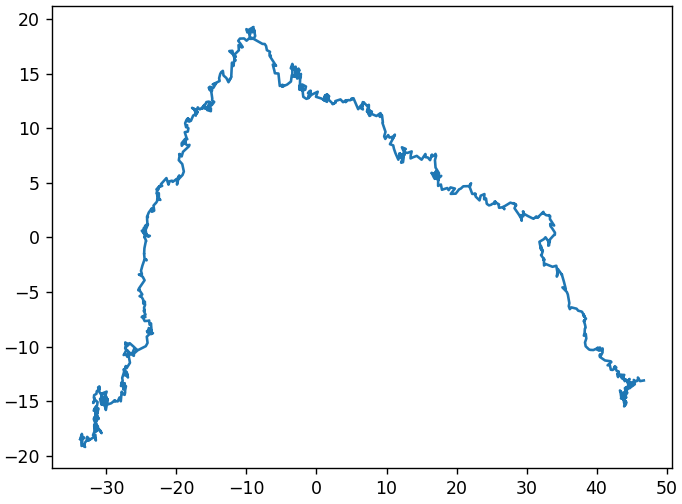
Абсолютные значения осей здесь не имеют особого смысла, но по относительным можно оценить существенность искажений.
Примеры многократного перекодирования
Исходный кот:

После одного пересохранения с качеством 50:

После любого последующего количества перекодирований с тем же качеством картинка не меняется. Теперь будем плавно снижать качество с 90 до 50 через 1:

Произошло примерно то же, что и на уже приводимом графике:
После одного пересохранения с качеством 20:

Плавно с 90 до 20:

Теперь 1000 раз со случайным качеством от 80 до 90:

10000 раз:
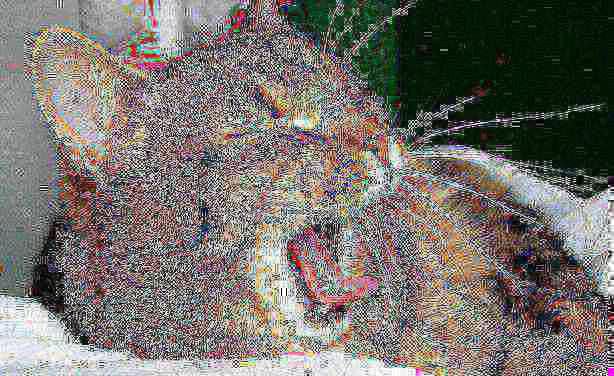
Анализ картинок группы VK
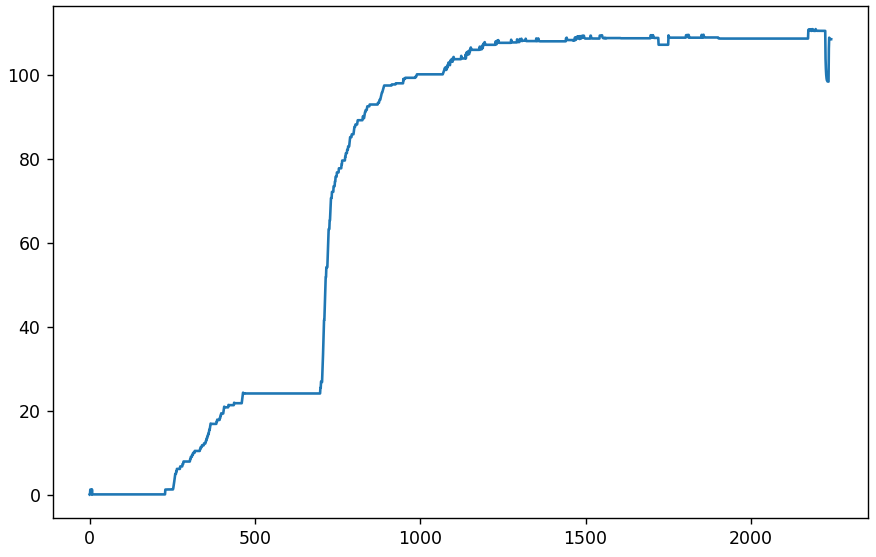
Приступим к анализу более 2000 картинок из группы VK. Сначала проверим среднее абсолютное отклонение от самой первой. По оси x — номер картинки (или день), по y — отклонение.
Перейдем к дифференциальному графику, показывающему среднее абсолютное отклонение соседних картинок.
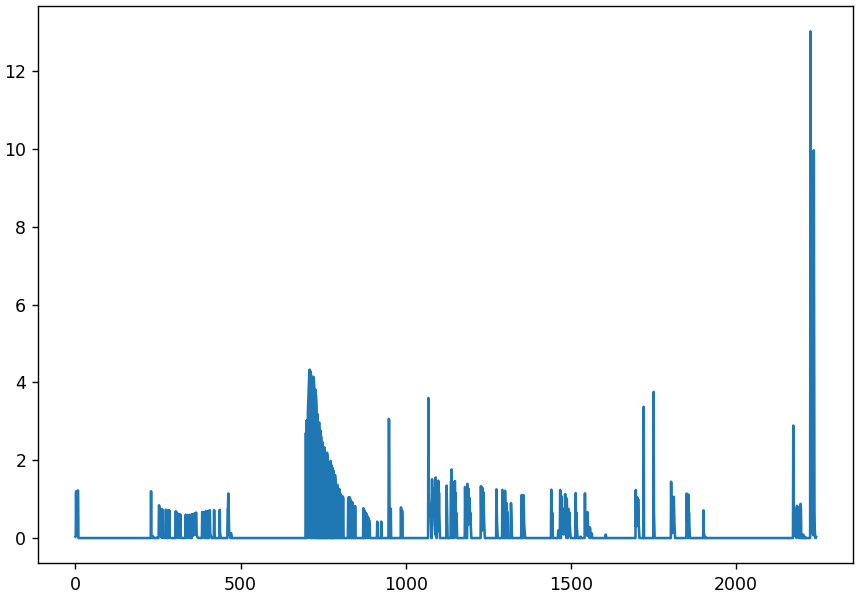
Небольшие колебания в начале — нормальное явление. До 232-й все идет хорошо, картинки полностью идентичны. А 233-я внезапно отличается в среднем на 1.23 для каждого пикселя (по шкале от 0 до 255). Это много. Возможно просто изменились таблицы квантования. Проверим.
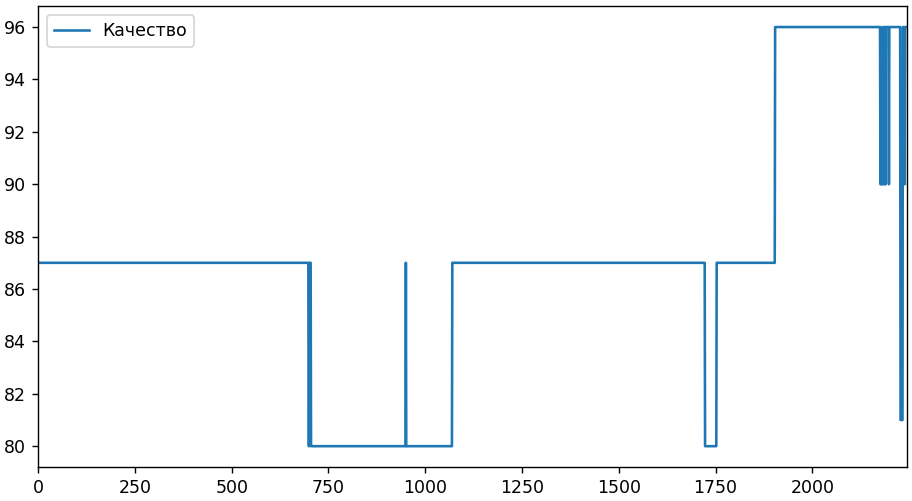
Да таблицы менялись. Но не раньше чем у 700-х. Тогда, возможно, происходило промежуточное скрытое перекодирование с низким качеством. Попробуем дважды перекодировать 232-ю. Для первого раза будем перебирать различные уровни качества, а для второго используем ту же таблицу квантования, что и для всех от 1-й до 700-х. Наша цель — получить картинку максимально похожую на 233-ю. На следующем рисунке по оси x — качество промежуточного перекодирования, по y — среднее абсолютное отклонение от 233-й.
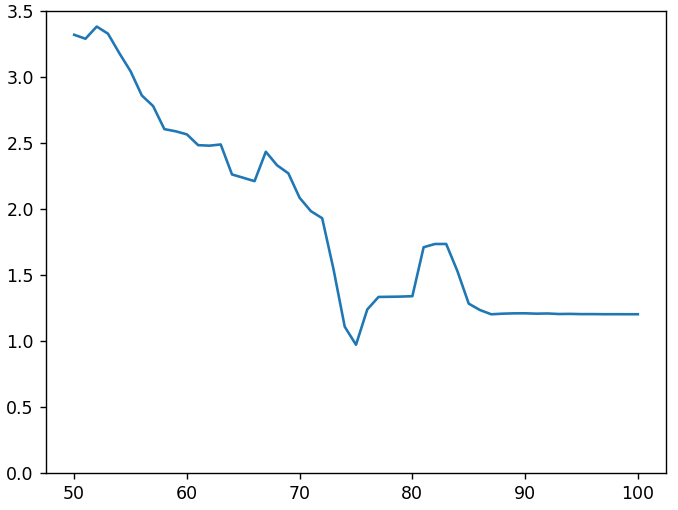
Хотя на графике и есть провал при качестве 75%, примерно равный 1, но все еще далеко от желаемого нуля. Добавление 2-го промежуточного этапа и изменение параметров субдискретизации (subsampling) не улучшило ситуацию.
С остальными картинками все примерно то же самое, плюс еще накладывается изменение таблиц квантования. То есть, в какой-то момент картинка резко меняется, затем за несколько дней стабилизируется, но только до тех пор, пока не происходит новый всплеск. Возможно, происходит изменение самого изображения на серверах. Не могу полностью исключить и причастность администратора группы.
К сожалению, я так и не выяснил, что же действительно происходило с изображением. По крайней мере, теперь уверен, что это было не просто пересохранение. Но, самое важное, стал лучше представлять происходящие процессы при кодировании и декодировании. Надеюсь, что и вы тоже.
Автор: Филипп Володин






