Введение
fBM расшифровывается как Fractional Brownian Motion (дробное броуновское движение). Но прежде чем начать говорить о природе, фракталах и процедурных рельефах, давайте на минуту углубимся в теорию.
Броуновское движение (Brownian Motion, BM), просто, без «дробности» — это движение, при котором положение объекта с течением времени меняется со случайными инкрементами (представьте последовательность position+=white_noise();). С формальной точки зрения BM является интегралом белого шума. Эти движения задают пути, которые являются случайными, но (статистически) самоподобными, т.е. приближенное изображение пути напоминает весь путь. Fractional Brownian Motion — это схожий процесс, в котором инкременты не полностью независимы друг от друга, а в этом процессе существует некая память. Если память имеет положительную корреляцию, то изменения в заданном направлении будут иметь тенденцию к будущим изменениям в том же направлении, и путь при этом будет плавнее, чем при обычном BM. Если память имеет отрицательную корреляцию, то за изменением в положительную сторону с большой вероятностью последует изменение в отрицательную, и путь окажется гораздо более случайным. Параметр, управляющий поведением памяти или интегрированием, а значит и самоподобием, её размерностью фрактала и спектром мощности, называется показателем Хёрста и обычно сокращается до H. С математической точки зрения H позволяет нам интегрировать белый шум только частично (допустим, выполнить только 1/3 интегрирования, отсюда и «дробность» в названии) для создания fBM под любые нужные нам характеристики памяти и внешний вид. H принимает значения в интервале от 0 до 1, которые описывают, соответственно, грубое и плавное fBM, а обычное BM получается при H=1/2.

Здесь функция fBM() использована для генерации рельефа, облаков, распределения деревьев, вариаций их цветов и деталей крон. «Rainforest», 2016: https://www.shadertoy.com/view/4ttSWf
Всё это очень теоретически, и в компьютерной графике fBM генерируется совершенно иначе, но я хотел объяснить теорию, потому что важно помнить о ней, даже когда создаёшь графику. Давайте посмотрим, как это делается на практике:
Как мы знаем, самоподобные структуры, в то же время являющиеся случайными, очень полезны для процедурного моделирования всевозможных природных явлений, от облаков до гор и текстур древесной коры. Интуитивно понятно, что фигуры в природе можно разложить на несколько крупных фигур, описывающих форму в целом, большее количество фигур среднего размера, искажающих основной контур или поверхность первоначальной фигуры, и ещё большее количество мелких фигур, добавляющих деталей контуру и форме предыдущих двух. Такой инкрементный способ добавления деталей объекту, обеспечивающий нам простой способ ограничения границ частотных диапазонов для изменения LOD (Level Of Detail, уровней детализации) и фильтрации/сглаживания фигур, позволяет легко писать код и создавать визуально красивые результаты. Поэтому он широко используется в фильмах и играх. Однако я не думаю, что fBM является хорошо понятным всем механизмом. В этой статье я опишу, как он работает и как используются его различные спектральные и визуальные характеристики при различных значениях его основного параметра H, и дополню всё это экспериментами и измерениями.
Базовая идея
Обычно (существует множество способов) fBM строятся вызовом детерминированной и сглаженной случайности при помощи выбранной разработчиком функции шума (value, градиентной, клеточной, Вороного, тригонометрической, симплексной, ..., и т.д., выбранный вариант здесь не особо важен), с последующим построением самоподобия. fBM реализуют, начиная с базового сигнала шума, постепенно добавляя к нему всё меньшие и меньшие детализированные вызовы шума. Примерно вот так:
float fbm( in vecN x, in float H )
{
float t = 0.0;
for( int i=0; i<numOctaves; i++ )
{
float f = pow( 2.0, float(i) );
float a = pow( f, -H );
t += a*noise(f*x);
}
return t;
}Это fBM в своём чистейшем виде. Каждый сигнал (или «волна») noise(), у которого мы имеем «numOctaves», аддитивно комбинируется с промежуточной суммой, но сжимается по горизонтали в два раза, что по сути снижает в два раза и его длину волны, а его амплитуда снижается экспоненциально. Такое накопление волн с координируемым уменьшением длины и амплитуды волны создаёт самоподобие, которое мы наблюдаем в природе. В конечном итоге, в любом заданном пространстве есть место только для нескольких больших изменений, но остаётся много места для всё более мелких изменений. Звучит вполне разумно. На самом деле, подобные проявления степенного закона встречаются в природе повсеместно.
Первое, что можно заметить — показанный выше код не совсем похож на большинство реализаций fBM, которые вы могли видеть в Shadertoy и других примерах кода. Приведённый ниже код аналогичен показанному выше, но намного популярнее, потому что обходится без затратных функций pow():
float fbm( in vecN x, in float H )
{
float G = exp2(-H);
float f = 1.0;
float a = 1.0;
float t = 0.0;
for( int i=0; i<numOctaves; i++ )
{
t += a*noise(f*x);
f *= 2.0;
a *= G;
}
return t;
}Итак, давайте для начала поговорим о «numOctaves». Поскольку длина волны каждого шума в два раза меньше, чем у предыдущего (а частота в два раза выше), обозначение того, что должно называться «numFrequencies», заменено на «numOctaves» как отсылка к музыкальному понятию: разделение одной октавы между двумя нотами соответствует удвоению частоты базовой ноты. Кроме того, fBM можно создавать инкрементом частоты каждого шума на величину, отличающуюся от двойки. В таком случае термин «октава» больше не будет технически корректным, но его всё равно используют. В некоторых случаях может даже потребоваться создание волн/шума с частотами, которые увеличиваются с постоянным линейным коэффициентом, а не геометрически, например, FFT (быстрое преобразование Фурье; его можно и в самом деле использовать для генерации периодических fBMs(), полезных при создании текстур океана). Но, как мы позже увидим, большинство базовых функций noise() может увеличивать частоты на величины, кратные двум, то есть нам потребуется очень мало итераций, а fBM всё равно будут красивыми. На самом деле, синтезирование fBM по одной октаве за раз позволяет нам быть очень эффективными — например, всего за 24 октавы/итерации можно создать fBM, покрывающее всю планету Земля с детализацией 2 метра. Если делать это при помощи линейно увеличивающихся частот, то потребуется на несколько порядков величин больше итераций.
Последнее примечание о последовательности частот: если мы перейдём от fi=2i к fi = 2⋅fi-1, то это даст нам определённую гибкость относительно удвоения частот (или уменьшения вполовину длин волн) — мы можем запросто развернуть цикл и немного изменить каждую октаву, например заменив 2.0 на 2.01, 1.99 и другие схожие значения, чтобы накапливаемые нули и пики разных волн шума не накладывались друг на друга ровно, что иногда создаёт нереалистичные паттерны. В случае 2D-fBM можно также немного повернуть область определения.
Итак, в новой программной реализации fBM() мы не только заменили генерацию частот со степенной формулировки на итеративный процесс, но и сменили экспоненциальную амплитуду (степенной закон) геометрическими рядами, управляемыми показателем «усиления» («gain») G. Необходимо выполнить преобразование из H в G, рассчитав G=2-H, что можно легко вывести из первой версии кода. Однако чаще программисты графики игнорируют показатель Хёрста H, или даже не знают о нём, и работают непосредственно со значениями G. Поскольку мы знаем, что H изменяется в интервале от 0 до 1, то G изменяется от 1 до 0.5. И в самом деле, большинство программистов задаёт в своих реализациях fBM постоянное значение G=0.5. Подобный код будет не таким гибким, как использующий переменный G, но на то имеются веские причины, и вскоре мы о них узнаем.
Самоподобие
Как говорилось выше, параметр H определяет самоподобие кривой. Разумеется, это статистическое самоподобие. То есть, в случае одномерного fBM(), если мы горизонтально приблизим камеру к графику на показатель U, то насколько нам нужно будет приблизиться к графику по вертикали на V, чтобы получить кривую, которая бы «выглядела» так же? Ну, поскольку a=f-H, то a⋅V = (f⋅U)-H = f-H⋅U-H = a⋅U-H, то есть V=U-H. Итак, если мы приближаем камеру к fBM на горизонтальный показатель 2, то по вертикали нужно изменить масштаб на 2-H. Но 2-H — это G! И это не совпадение: при использовании G для масштабирования амплитуд шума мы по определению строим самоподобие fBM с коэффициентом масштабирования G = 2-H.
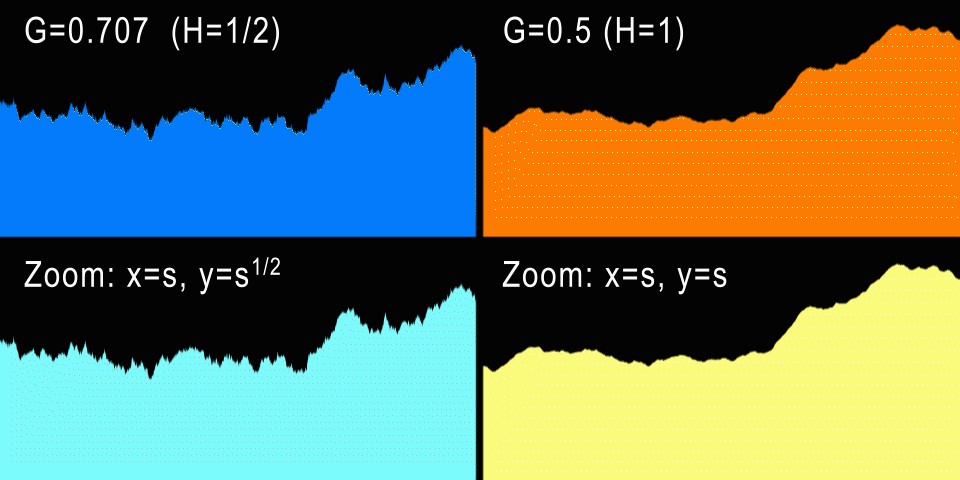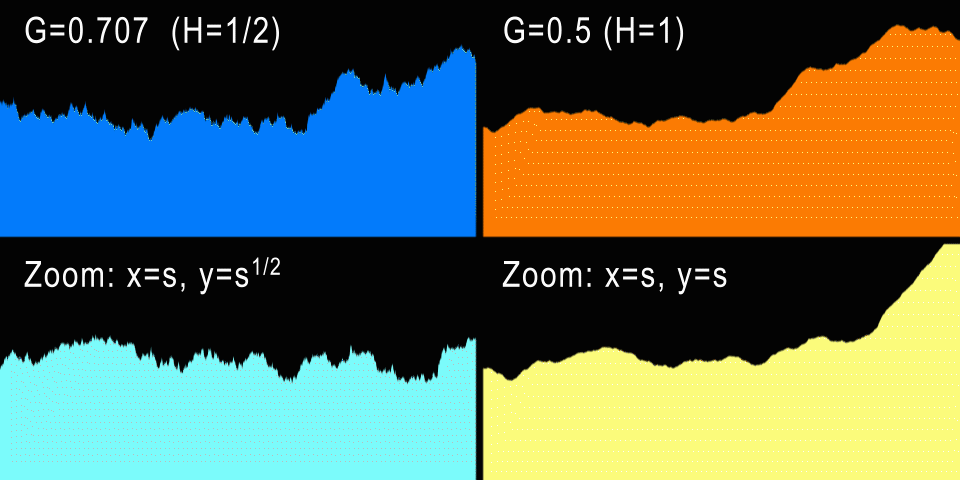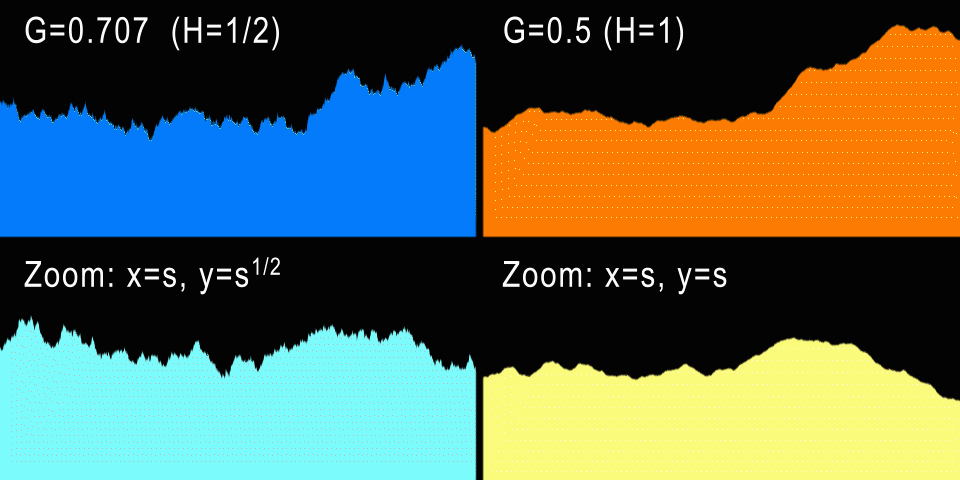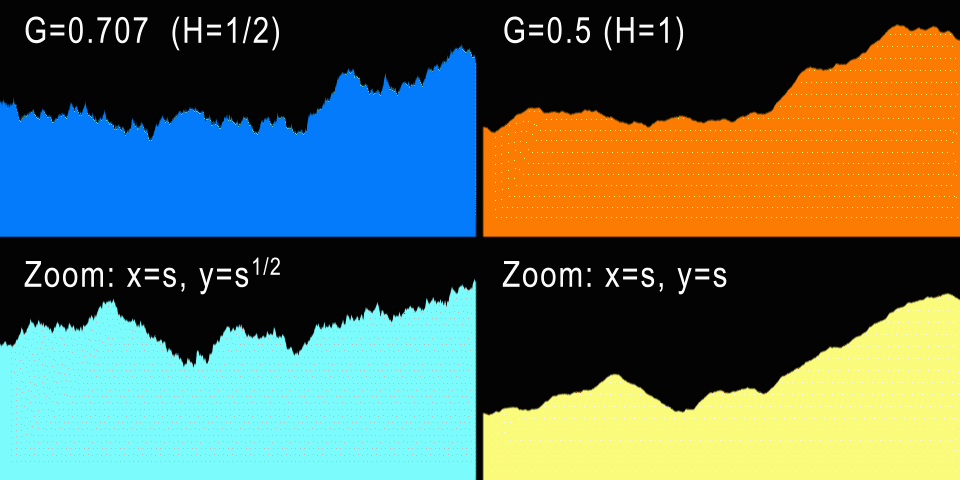
Слева показано броуновское движение (H=1/2) и анизотропный зум. Справа fBM (H=1) и изотропный зум.
Код: https://www.shadertoy.com/view/WsV3zz
А что насчёт процедурных гор? Стандартное броуновское движение имеет значение H=1/2, что даёт нам G=0.707107… При таких значениях генерируется кривая, которая при увеличении выглядит точно так же, если анизотропно отмасштабирована по X и Y (если это одномерная кривая). И в самом деле: для каждого коэффициента горизонтального зума U нам потребуется отмасштабировать кривую по вертикали на V=sqrt(U), что не очень естественно. Однако графики фондовых бирж очень часто приближаются к H=1/2, потому что в теории каждый инкремент или декремент значения акций не зависит от предыдущих изменений (не забывайте, что BM — это процесс без памяти). Разумеется, на практике определённые зависимости присутствуют, и эти кривые ближе к H=0.6.
Но естественный процесс содержит в себе больше «памяти», и самоподобие в нём гораздо изотропнее. Например, более высокая гора шире в своём основании на ту же величину, т.е. горы обычно не растягиваются и не становятся тоньше. Поэтому это даёт нам понять, что для гор G должен быть равен 1/2 — одинаковый зум по горизонтали и вертикали. Это соответствует H=1, то есть профили гор должны быть плавнее, чем кривая фондовой биржи. На самом деле так и есть, и чуть позже мы измерим настоящие профили, чтобы подтвердить это. Но по опыту мы знаем, что G=0.5 создаёт красивые фрактальные рельефы и облака, поэтому G=0.5 и в самом деле является самым популярным значением G для всех реализаций fbm.
Но теперь у нас есть более глубокое понимание H, G и fBM в целом. Мы знаем, что если значение G ближе к 1, то fBM будет даже безумнее, чем чистое BM. И в самом деле: при G=1, что соответствует H=0, мы получаем самое шумное fBM из всех.
Все эти параметризированные функции fBM имеют названия, например, «розовый шум» при H=0, G=1 или «коричневый шум» при H=1/2, G=sqrt(2), которые унаследованы из области обработки цифровых сигналов (Digital Signal Processing) и хорошо известны людям, имеющим проблемы со сном. Давайте углубимся в DSP и вычислим спектральные характеристики, чтобы получить более глубокое понимание fBM.
Взгляд с точки зрения обработки сигналов
Если задуматься об анализе Фурье, или об аддитивном синтезе звука, то показанная выше реализация fBM() похожа на реализацию обратного преобразования Фурье (Inverse Fourier Transform), которое дискретно, как и дискретное преобразование Фурье (DFT), но очень разрежено и использует другую базовую функцию (по сути оно очень отличается от IFT, но позвольте мне объяснить). На самом деле, мы можем генерировать fBM(), рельефы компьютерной графики и даже поверхности океана при помощи IFFT, но это быстро становится очень затратным проектом. Причина заключается в том, что IFFT аддитивно комбинирует не волны шума, а синусоиды, но синусоиды не очень эффективно заполняют спектр мощности энергии, потому что каждая синусоида влияет на одну частоту. Однако функции шума имеют широкие спектры, покрывающие одной волной длинные интервалы частот. И градиентный шум, и Value-шум имеют такие богатые и плотные графики плотности спектров. Взгляните на графики:
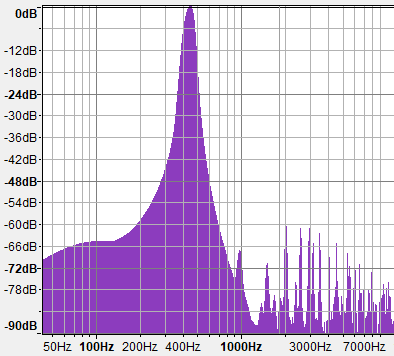
Синусоида
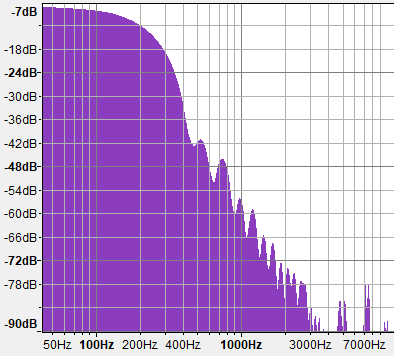
Value-шум
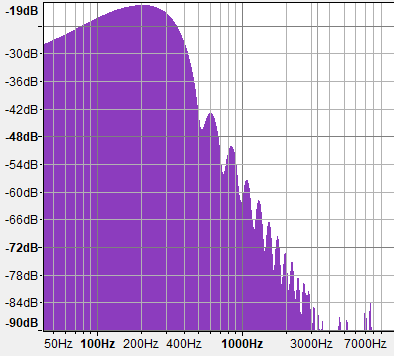
Градиентный шум
Заметьте, что в спектре и Value-шума, и градиентного шума основная часть энергии сконцентрирована в нижних частотах, но он шире — идеальный выбор для быстрого заполнения всего спектра несколькими смещёнными и отмасштабированными копиями. Другая проблема fBM на основе синусоид заключается в том. что оно, разумеется, генерирует повторяющиеся паттены, которые чаще всего нежелательны, хотя и могут пригодиться для генерации бесшовных текстур. Преимущество fBM() на основе sin() заключается в том, что оно сверхпроизводительно, потому что тригонометрические функции выполняются в железе гораздо быстрее, чем построение шума при помощи многочленов и хешей/lut, поэтому иногда по-прежнему стоит использовать fBM на основе синусоид из соображений производительности, даже если при этом создаются плохие ландшафты.
Теперь давайте взглянем на графики плотности спектров для fBM с разными значениями H. Обратите особое внимание на отметки на вертикальной оси, потому что все три графика нормализованы и не описывают одинаковые склоны, хотя на первый взгляд выглядят почти одинаковыми. Если мы обозначим отрицательный склон этих графиков спектров как «B», то поскольку эти графики имеют логарифмический масштаб, спектр будет следовать степенному закону вида f-B. В этом тесте я использую 10 октав обычного градиентного шума для построения показанных ниже fBM.
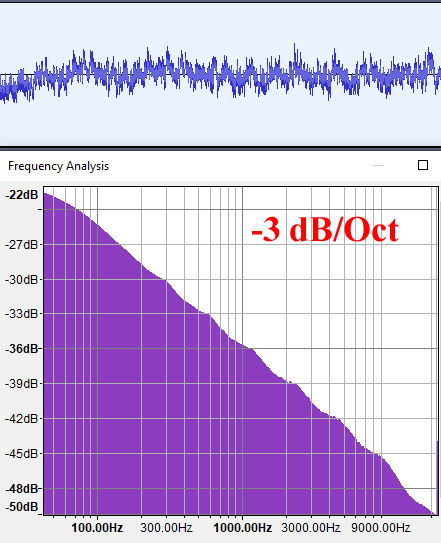
G=1.0 (H=0)
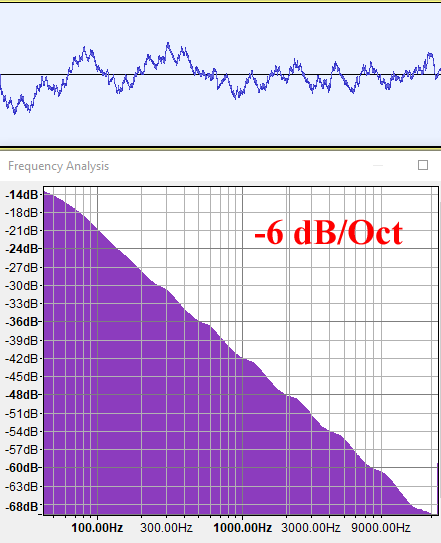
G=0.707 (H=1/2)
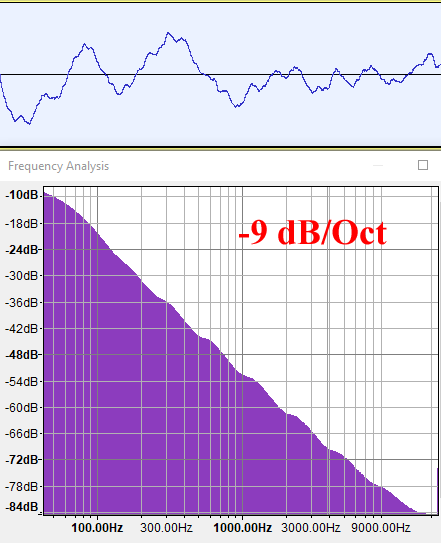
G=0.5 (H=1)
Как мы видим, энергия fBM с H=0 (G=1) затухает по 3 дБ на октаву, или, по сути, обратно по значению к частоте. Это степенной закон f-1 (B=1), который называется «розовым шумом» и звучит как дождь.
fBM() с H=1/2 (G=0.707) генерирует спектр, который затухает быстрее, по 6 дБ на октаву, то есть он имеет меньше высоких частот. Он и в самом деле звучит глубже, как будто вы слышите дождь, но на этот раз из своей комнаты с закрытыми окнами. Затухание 6 дБ/октава означает, что энергия пропорциональна f-2 (B=2), и это в самом деле является характеризацией броуновского движения в DSP.
Наконец, наше любимое fBM из компьютерной графики с H=1 (G=0.5) генерирует график плотности спектров с затуханием 9 дБ/октава, то есть энергия обратно пропорциональна кубу частоты (f-3, B=3). Это сигнал с постоянно низкой частотой, который соответствует процессу с памятью с положительной корреляцией, о которой мы говорили в начале. Такой тип сигнала не имеет собственного названия, поэтому у меня есть искушение назвать его «жёлтым шумом» (просто потому, что это название больше ни для чего не используется). Как мы знаем, он изотропен, а значит, моделирует множество самоповторяющихся природных форм.
На самом деле, я подтвержу свои слова о схожести с природой, сделав измерения, приведённые в следующем разделе статьи.
| Название | H | G=2-H | B=2H+1 | дБ/окт | Звук |
| Синий | - | - | +1 | +3 | Распыляемая вода. Ссылка |
| Белый | - | - | 0 | 0 | Ветер в листьях. Ссылка |
| Розовый | 0 | 1 | -1 | -3 | Дождь. Ссылка |
| Коричневый | 1/2 | sqrt(2) | -2 | -6 | Дождь, слышимый из дома. Ссылка |
| Жёлтый | 1 | 1/2 | -3 | -9 | Двигатель за дверью |
Измерения
Сначала должен предупредить, что это будет очень ненаучный эксперимент, но я всё равно хочу им поделиться. Я взял фотографии горных гряд, расположенных параллельно плоскости изображения, чтобы избежать перспективного искажения. Затем я разделил изображения на чёрный и белый цвета, а затем преобразовал поверхность контакта неба и гор в 1D-сигнал. Затем я интерпретировал его как звуковой файл WAV и вычислил его график частот, как в случае с синтетическими сигналами fBM(), которые анализировал выше. Я выбирал изображения с достаточно большим разрешением, чтобы у алгоритма FFT были значимые данные для работы.

Источник: Greek Reporter

Источник: Wikipedia




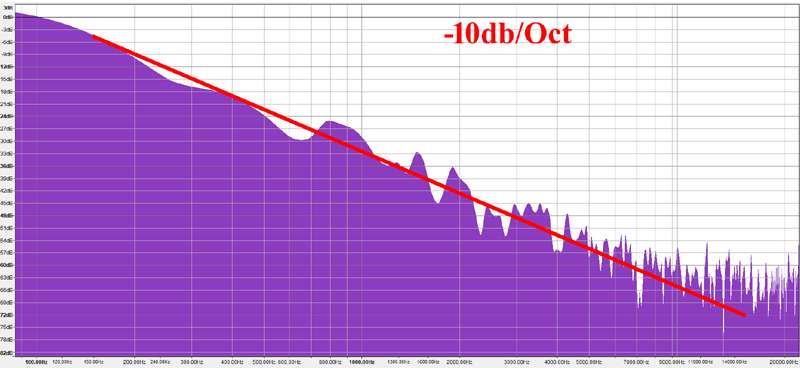
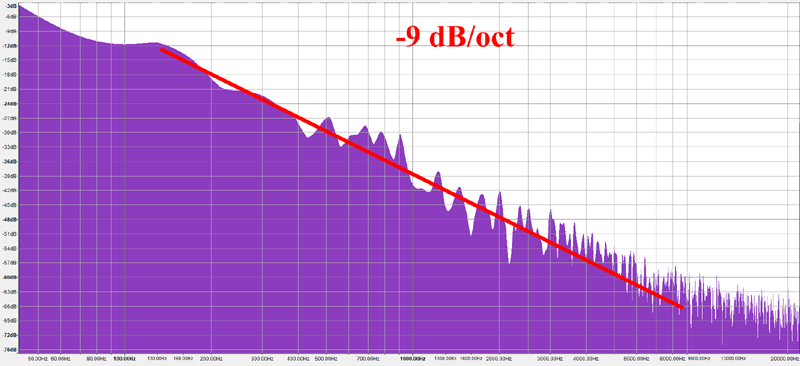
Похоже, результаты действительно указывают на то, что профили гор следуют распределению частот -9 дБ/октава, что соответствует B=-3 или H=1 или G=0.5, или, другими словами, жёлтому шуму.
Разумеется, эксперимент был не строгим, но он подтверждает наше интуитивное понимание и то, что мы уже знаем из опыта и работы с компьютерной графикой. Но надеюсь, теперь мы начали разбираться в этом лучше!
Автор: PatientZero
