Месяц Posit объявлен на Хабре открытым, а значит я не могу пройти мимо и проигнорировать обрушившуюся на них критику. В предыдущих сериях:
Новый подход может помочь нам избавиться от вычислений с плавающей запятой
Posit-арифметика: победа над floating point на его собственном поле. Часть 1
Posit-арифметика: победа над floating point на его собственном поле. Часть 2
Испытания Posit по-взрослому
Думаю многие из вас могут с ходу вспомнить хотя бы один случай из истории, когда революционные идеи на момент своего становления наталкивались на неприятие сообществом экспертов. Как правило, виной такому поведению выступает обширный багаж уже накопленных знаний, не позволяющий взглянуть на старую проблему в новом свете. Таким образом, новая идея проигрывает по характеристикам устоявшимся подходам, ведь оценивается она только теми метриками, которые считались важными на предыдущем этапе развития.
Именно с таким неприятием на сегодняшний день сталкивается формат Posit: критикующие зачастую просто “не туда смотрят“ и даже банально неправильно используют Posit в своих экспериментах. В данной статье я попытаюсь объяснить почему.
О достоинствах Posit было сказано уже не мало: математическая элегантность, высокая точность на значениях с низкой экспонентой, широкий диапазон значений, только одно бинарное представление NaN и нуля, отсутствие субнормальных значений, борьба с overflow/underflow. Не мало было высказано и критики: никудышная точность для очень больших или очень маленьких значений, сложный формат бинарного представления и конечно отсутствие аппаратной поддержки.
Я не хочу повторять уже сказанные аргументы, вместо этого постараюсь сосредоточиться на том аспекте, который как правило упускают из виду.
Правила игры изменились
Стандарт IEEE 754 описывает числа с плавающей запятой, реализованный в Intel 8087 почти 40 лет назад. По меркам нашей индустрии это невероятный срок; с тех пор изменилось практически все: производительность процессоров, стоимость памяти, объемы данных и масштабы вычислений. Формат Posit был разработан не просто как лучшая версия IEEE 754, а как подход к работе с числами, отвечающий новым требованиям времени.
Высокоуровневая задача осталась прежней – всем нам требуются эффективные вычисления над полем рациональных чисел с минимальной потерей точности. Но условия, в которой решается поставленная задача радикально изменились.
Во-первых, изменились приоритеты для оптимизации. 40 лет назад производительность компьютеров почти полностью зависела от производительности процессора. Сегодня производительность большинства вычислений упираются в память. Чтобы убедится в этом, достаточно взглянуть на ключевые направления развития процессоров последних десятилетий: трёхуровневое кеширование, спекулятивное выполнение, конвейеризация вычислений, предсказывание ветвлений. Все эти подходы направлены на достижение высокой производительности в условиях быстрых вычислений и медленного доступа к памяти.

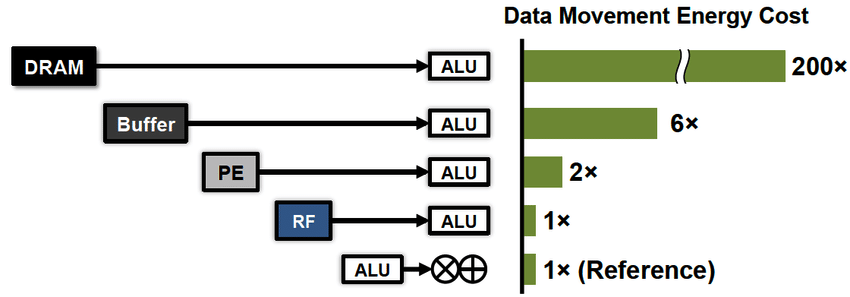
Во-вторых, на первый план вышло новое требование – эффективное энергопотребление. За последние десятилетия технологии горизонтального масштабирования вычислений продвинулись вперед настолько, что нас начала волновать не столько скорость этих вычислений, сколько счет за электричество. Здесь мне следует подчеркнуть важную для понимания деталь. С точки зрения энергоэффективности вычисления стоят дешево, ведь регистры процессора находятся очень близко к его вычислителям. Гораздо дороже прийдется расплачиваться за передачу данных, как между процессором и памятью (x100), так и на дальние расстояния (x1000...).
Вот лишь один из примеров научного проекта, который планирует использовать Posit:

Эта сеть телескопов генерирует 200 петабайт данных в секунду, на обработку которых уходит мощность небольшой электростанции – 10 мегаватт. Очевидно, что для таких проектов сокращение объемов данных и энергопотребления является критическим.
В самое начало
Так что же предлагает стандарт Posit? Чтобы понять это, нужно вернуться в самое начало рассуждений и понять, что подразумевается под точностью чисел с плавающей запятой.
На самом деле существует два разных аспекта имеющих отношение к точности. Первый аспект, это точность вычислений – то, насколько сильно отклоняются результаты вычислений во время выполнения различных операций. Второй аспект, это точность представления – то, насколько сильно искажается исходное значение в момент преобразования из поля рациональных чисел в поле чисел с плавающей запятой конкретного формата.
Теперь будет важный для осознания момент. Posit – это в первую очередь формат представления рациональных чисел, а не способ выполнения операций над ними. Другими словами, Posit – это формат сжатия рациональных чисел с потерями. Вы могли слышать утверждение, что 32-битные Posit – это хорошая альтернатива 64-битным Float. Так вот, речь идет именно о сокращении необходимого объема данных в два раза для хранения и передачи одного и того же набора чисел. В два раза меньше памяти – почти в 2 раза меньше энергопотребления и высокая производительность процессора благодаря меньшим ожиданиям доступа к памяти.
Второй конец палки
Здесь у вас должен был возникнуть закономерный вопрос: какой смысл от эффективного представления рациональных чисел, если он не позволяет производить вычисления с высокой точностью.
На самом деле, способ выполнения точных вычислений есть, и он называется Quire. Это другой формат представления рациональных чисел, неразрывно связанный с Posit. В отличии от Posit, формат Quire предназначен именно для вычислений и для хранения промежуточных значений в регистрах, а не в основной памяти.

Если в вкратце, то Quire представляют из себя не что иное, как широкий целочисленный аккумулятор (fixed point arithmetic). Единице, как бинарному представлению Quire соответствует минимальное положительное значение Posit. Максимальное значение Quire соответствует максимальному значению Posit. Каждое значение Posit имеет однозначное представление в Quire без потери точности, но не каждое значение Quire может быть представлено в Posit без потери точности.
Преимущества Quire очевидны. Они позволяют выполнять операции с несравнимо более высокой точностью чем Float, а для операций сложения и умножения какой-либо потери точности не будет вообще. Цена, которую за это приходится платить – широкие регистры процессора (32-битным Posit с es=2 соответствуют 512-битные Quire), но для современных процессоров это не является серьезной проблемой. И если 40 лет назад вычисления над 512 битными целыми числами казались неприемлемой роскошью, то сегодня это является скорее адекватной альтернативой широкому доступу к памяти.
Собираем пазл
Таким образом, Posit предлагают не просто новый стандарт в виде альтернативы Float/Double, а скорее новый подход по работе с числами. Новизна подхода в том, что используется два различных формата представления, один для хранения и передачи чисел – Posit, и другой для вычислений и их промежуточных значений – Quire.
Когда вы решаем практические задачи с применением чисел с плавающей запятой, с точки зрения процессора работу с ними можно представить в виде набора следующих действий:
- Прочитать значения чисел из памяти.
- Выполнить некоторую последовательность операций. Иногда количество операций является достаточно большим. При этом, все промежуточные значения вычислений хранятся в регистрах.
- Записать результат операций в память.
В случае применения Float/Double точность теряется на каждой операции. В случае применения Posit+Quire потеря точности во время вычислений ничтожна. Она теряется только на последнем этапе, в момент преобразования значения Quire в Posit. Именно по-этому большинство проблем “накопления ошибки” для Posit+Quire просто не актуальны.
В отличии от Float/Double, при применения Posit+Quire мы как правило можем позволить себе более компактное представления чисел. Как результат – более быстрый доступ к данным из памяти (лучше производительность) и более эффективное хранение и передача информации.
Соотношение Мюллера
В качестве наглядной демонстрации, я приведу лишь один пример – классическое рекуррентное соотношение Мюллера, придуманное специально для того, чтобы демонстрировать, как накопление ошибки при вычислениях с плавающей запятой радикально искажает результат вычислений.

В случае применения арифметики с произвольной точностью, рекуррентная последовательность должна сводиться к значению 5. В случае арифметики с плавающей запятой вопрос лишь в том, на какой именно итерации результаты вычислений начнут иметь неадекватно большое отклонение.
Я провел эксперимент для IEEE 754 с одинарной и двойной точностью, а также для 32-битных Posit+Quire. Вычисления проводились в арифметике Quire, но каждое значение в таблице преобразовано в Posit.
# float(32) double(64) posit(32) ------------------------------------------------ 0 4.000000 4.000000 4 1 4.250000 4.250000 4.25 2 4.470589 4.470588 4.470588237047195 3 4.644745 4.644737 4.644736856222153 4 4.770706 4.770538 4.770538240671158 5 4.859215 4.855701 4.855700701475143 6 4.983124 4.910847 4.91084748506546 7 6.395432 4.945537 4.94553741812706 8 27.632629 4.966962 4.966962575912476 9 86.993759 4.980042 4.980045706033707 10 99.255508 4.987909 4.98797944188118 11 99.962585 4.991363 4.992770284414291 12 99.998131 4.967455 4.99565589427948 13 99.999908 4.429690 4.997391253709793 14 100.000000 -7.817237 4.998433947563171 15 100.000000 168.939168 4.9990600645542145 16 100.000000 102.039963 4.999435931444168 17 100.000000 100.099948 4.999661535024643 18 100.000000 100.004992 4.999796897172928 19 100.000000 100.000250 4.999878138303757 20 100.000000 100.000012 4.999926865100861 21 100.000000 100.000001 4.999956130981445 22 100.000000 100.000000 4.999973684549332 23 100.000000 100.000000 4.9999842047691345 24 100.000000 100.000000 4.999990522861481 25 100.000000 100.000000 4.999994307756424 26 100.000000 100.000000 4.999996602535248 27 100.000000 100.000000 4.999997943639755 28 100.000000 100.000000 4.999998778104782 29 100.000000 100.000000 4.99999925494194 30 100.000000 100.000000 4.999999552965164 31 100.000000 100.000000 4.9999997317790985 32 100.000000 100.000000 4.999999850988388 33 100.000000 100.000000 4.999999910593033 34 100.000000 100.000000 4.999999940395355 35 100.000000 100.000000 4.999999970197678 36 100.000000 100.000000 4.999999970197678 37 100.000000 100.000000 5 38 100.000000 100.000000 5 39 100.000000 100.000000 5 40 100.000000 100.000000 5 41 100.000000 100.000000 5 42 100.000000 100.000000 5 43 100.000000 100.000000 5 44 100.000000 100.000000 5 45 100.000000 100.000000 5 46 100.000000 100.000000 5 47 100.000000 100.000000 5 48 100.000000 100.000000 5 49 100.000000 100.000000 5 50 100.000000 100.000000 5 51 100.000000 100.000000 5 52 100.000000 100.000000 5.000000059604645 53 100.000000 100.000000 5.000000983476639 54 100.000000 100.000000 5.000019758939743 55 100.000000 100.000000 5.000394910573959 56 100.000000 100.000000 5.007897764444351 57 100.000000 100.000000 5.157705932855606 58 100.000000 100.000000 8.057676136493683 59 100.000000 100.000000 42.94736957550049 60 100.000000 100.000000 93.35784339904785 61 100.000000 100.000000 99.64426326751709 62 100.000000 100.000000 99.98215007781982 63 100.000000 100.000000 99.99910736083984 64 100.000000 100.000000 99.99995517730713 65 100.000000 100.000000 99.99999809265137 66 100.000000 100.000000 100 67 100.000000 100.000000 100 68 100.000000 100.000000 100 69 100.000000 100.000000 100 70 100.000000 100.000000 100
Как видно из таблицы, 32-битные Float сдаются уже на седьмом значении, а 64-битные Float продержались до 14 итерации. В тоже время, вычисления для Posit с применением Quire возвращают стабильный результат вплоть до 58 итерации!
Мораль
Для многих практических случаев и при правильном применении формат Posit действительно позволяет с одной стороны экономить на памяти, сжимая числа лучше, чем это делает Float, с другой стороны обеспечивать лучшую точность вычислений благодаря применению Quire.
Но это только теория! Когда дело касается точности или производительности, всегда делайте тесты прежде чем слепо довериться тому или иному подходу. Ведь на практике конкретно ваш случай будет оказываться исключительным гораздо чаще, чем в теории.
Ну и не забывайте первый закон Кларка (вольная интерпретация): Когда уважаемый и опытный эксперт утверждает, что новая идея будет работать, то он почти наверняка прав. Когда он утверждает, что новая идея работать не будет — то он, весьма вероятно, ошибается. Я не считаю себя опытным экспертом, чтобы позволить вам полагаться на мое мнение, но прошу вас с настороженностью относиться к критике даже опытных и уважаемых людей. Ведь дьявол кроется в деталях, и даже опытные люди могут их упустить.
Автор: Иващенко Иван






