Элементарная симуляция кастомного физического взаимодействия на python + matplotlib

в 9:01, , рубрики: Matlab, python, взаимодействие, математика, моделирование, физика

Привет!

Тут мы опишем работу некоторого поля а затем сделаем пару красивых фичей (тут все ОЧЕНЬ просто).

Элементарная симуляция кастомного физического взаимодействия на python + matplotlib - 1

Что будет в этой статье.

Общий случай:

  1. Опишем базу, а именно работу с векторами (велосипед для тех, у кого нет под рукой numpy)
  2. Опишем материальную точку и поле взаимодействия

Частный случай (на основе общего):

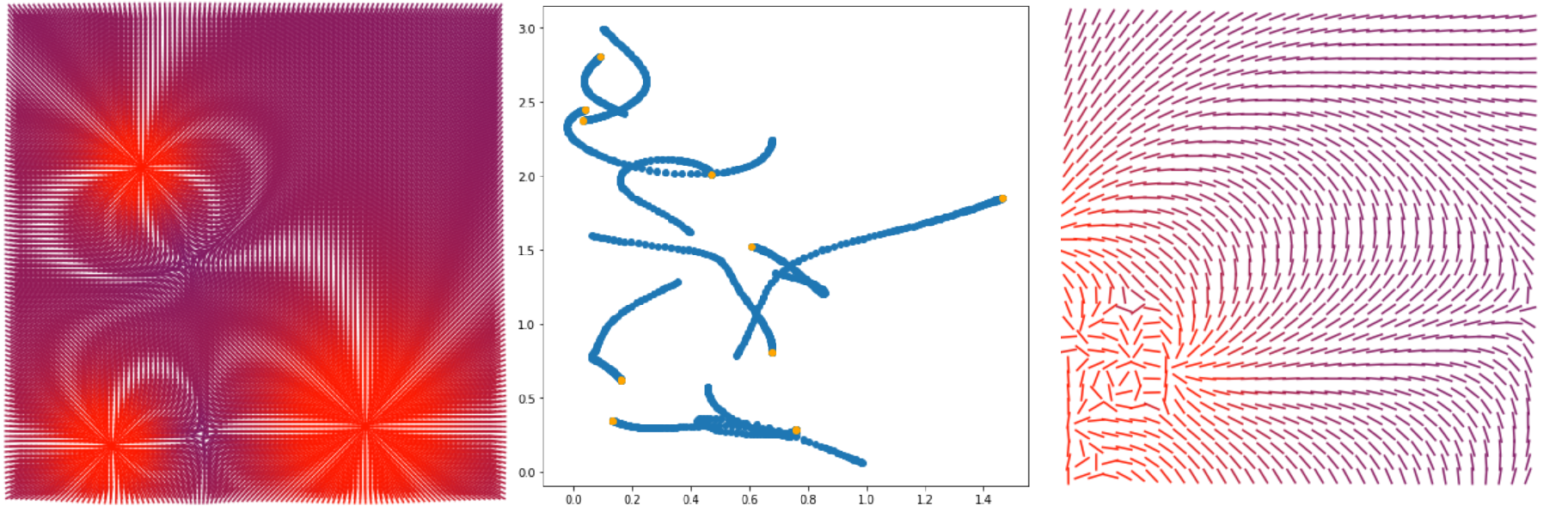
  1. Сделаем визуализацию векторного поля напряженности электромагнитного поля (первая и третья картинки)
  2. Сделаем визуализацию движения частиц в электромагнитном поле

Встретимся под катом!

Программирование теоретических основ

Вектор

Основа всех основ — вектор (особенно в нашем случае). Поэтому именно с описания вектора мы и начнем. Что нам нужно? Арифметические операции над вектором, расстояние, модуль, и пару технических вещей. Вектор мы будем наследовать от list. Так выглядит его инициализация: 

class Vector(list):
    def __init__(self, *el):
        for e in el:
            self.append(e)

То есть теперь мы можем создать вектор с помощью 

v = Vector(1, 2, 3)

Зададим арифметическую операцию сложение:

class Vector(list):
...
    def __add__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] + other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self + other

Отлично:

v1 = Vector(1, 2, 3)
v2 = Vector(2, 57, 23.2)
v1 + v2
>>> [3, 59, 26.2]

Аналогично зададим все арифметические операции (полный код вектора будет ниже). Теперь нужна функция расстояния. Я мог бы сделать деревенское dist(v1, v2) — но это не красиво, поэтому переопределим оператор %:

class Vector(list):
...
    def __mod__(self, other):
        return sum((self - other) ** 2) ** 0.5

Отлично:

v1 = Vector(1, 2, 3)
v2 = Vector(2, 57, 23.2)
v1 % v2
>>> 58.60068258988115

Еще нам нужна пара методов для более быстрого генерирования вектора и красивого выхода. Хитрого тут ничего нет, поэтому вот весь код класса Vector:

Весь код класса Vector

class Vector(list):
    def __init__(self, *el):
        for e in el:
            self.append(e)

    def __add__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] + other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self + other

    def __sub__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] - other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self - other

    def __mul__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] * other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self * other

    def __truediv__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] / other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self / other

    def __pow__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] ** other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self ** other

    def __mod__(self, other):
        return sum((self - other) ** 2) ** 0.5

    def mod(self):
        return self % Vector.emptyvec(len(self))

    def dim(self):
        return len(self)
    
    def __str__(self):
        if len(self) == 0:
            return "Empty"
        r = [str(i) for i in self]
        return "< " + " ".join(r) + " >"
    
    def _ipython_display_(self):
        print(str(self))

    @staticmethod
    def emptyvec(lens=2, n=0):
        return Vector(*[n for i in range(lens)])

    @staticmethod
    def randvec(dim):
        return Vector(*[random.random() for i in range(dim)])

Материальная точка

Тут по идее все просто — у точки есть координаты, скорость и ускорение (для простоты). Помимо этого у нее есть масса и набор кастомных параметров (к примеру для электромагнитного поля нам не помешает заряд, но вам никто не мешает задать хоть спин).

Инициализация будет такой:

class Point:
    def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties):
        self.coords = coords
        if speed is None:
            self.speed = Vector(*[0 for i in range(len(coords))])
        else:
            self.speed = speed
        self.acc = Vector(*[0 for i in range(len(coords))])
        self.mass = mass
        self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
        self.q = q
        for prop in properties:
            setattr(self, prop, properties[prop])

А чтобы передвигать, обездвиживать и ускорять нашу точку напишем следующие методы:

class Point:
...
    def move(self, dt):
        self.coords = self.coords + self.speed * dt

    def accelerate(self, dt):
        self.speed = self.speed + self.acc * dt

    def accinc(self, force):  # Зная сообщаемую силу мы получаем нужное ускорение
        self.acc = self.acc + force / self.mass
    
    def clean_acc(self):
        self.acc = self.acc * 0

Отлично, сама по себе точка сделана.

Код Point (с красивым выводом)

class Point:
    def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties):
        self.coords = coords
        if speed is None:
            self.speed = Vector(*[0 for i in range(len(coords))])
        else:
            self.speed = speed
        self.acc = Vector(*[0 for i in range(len(coords))])
        self.mass = mass
        self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
        self.q = q
        for prop in properties:
            setattr(self, prop, properties[prop])

    def move(self, dt):
        self.coords = self.coords + self.speed * dt

    def accelerate(self, dt):
        self.speed = self.speed + self.acc * dt

    def accinc(self, force):
        self.acc = self.acc + force / self.mass
    
    def clean_acc(self):
        self.acc = self.acc * 0
    
    def __str__(self):
        r = ["Point {"]
        for p in self.__params__:
            r.append("  " + p + " = " + str(getattr(self, p)))
        r += ["}"]
        return "n".join(r)

    def _ipython_display_(self):
        print(str(self))

Результат:
Элементарная симуляция кастомного физического взаимодействия на python + matplotlib - 2

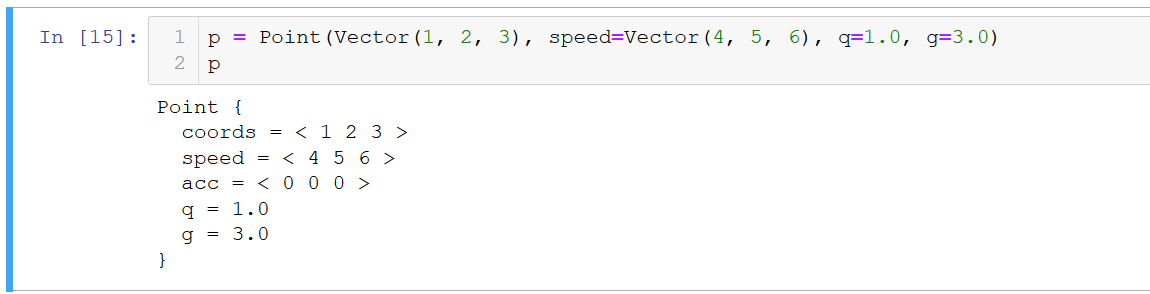
Поле взаимодействия

Полем взаимодействия мы зовем объект, включающий в себя множество всех материальных точек и оказывающий на них силу. Мы рассмотрим частный случай нашей замечательной вселенной, поэтому у нас будет одно кастомное взаимодействие (разумеется, это легко расширить). Объявим конструктор и добавление точки: 

class InteractionField:
    def __init__(self, F):  # F - это кастомное взаимодействие, F(p1, p2, r), p1, p2 - точки, r - расстояние между ними
        self.points = []
        self.F = F

    def append(self, *args, **kwargs):
        self.points.append(Point(*args, **kwargs))

Теперь самое интересное — объявить функцию, которая возвращает «напряженность» в этой точке. Хотя это понятие относится к электромагнитному взаимодействию, в нашем случае это некоторый абстрактный вектор, вдоль которого мы и будем двигать точку. При этом у нас будет свойство точки q, в частном случае — заряд точки (в общем — что захотим, даже вектор). Итак, что такое напряженность в точке C? Что-то типа этого:

$ vec E(vec C)=sum {vec F_i(vec C)} $

То есть напряженность в точке $ vec C $ равна сумме сил всех материальных точек действующих на некоторую единичную точку.

class InteractionField:
...
    def intensity(self, coord):
        proj = Vector(*[0 for i in range(coord.dim())])
        single_point = Point(Vector(), mass=1.0, q=1.0)  # А вот и наша единичная точка (у нее нет координат, так как расстояние уже передается в F, а значит они нам не нужны)
        for p in self.points:
            if coord % p.coords < 10 ** (-10):
                continue
            d = p.coords % coord
            fmod = self.F(single_point, p, d) * (-1)    # Тут мы получаем -модуль силы
            proj = proj + (coord - p.coords) / d * fmod  # суммируем
        return proj

На этом моменте уже можно нарисовать векторное поле, но мы будем делать это в конце. Теперь сделаем шаг нашего взаимодействия

class InteractionField:
...
    def step(self, dt):
        self.clean_acc()
        for p in self.points:
            p.accinc(self.intensity(p.coords) * p.q)
            p.accelerate(dt)
            p.move(dt)

Тут все просто. Для каждой точки мы определяем напряженность в этих координатах а затем определяем конечную силу на ЭТУ материальную точку:

$ vec F=vec E * q $

Определим недостающие функции.

Весь код InteractionField


class InteractionField:
    def __init__(self, F):
        self.points = []
        self.F = F

    def move_all(self, dt):
        for p in self.points:
            p.move(dt)

    def intensity(self, coord):
        proj = Vector(*[0 for i in range(coord.dim())])
        single_point = Point(Vector(), mass=1.0, q=1.0)
        for p in self.points:
            if coord % p.coords < 10 ** (-10):
                continue
            d = p.coords % coord
            fmod = self.F(single_point, p, d) * (-1)
            proj = proj + (coord - p.coords) / d * fmod
        return proj

    def step(self, dt):
        self.clean_acc()
        for p in self.points:
            p.accinc(self.intensity(p.coords) * p.q)
            p.accelerate(dt)
            p.move(dt)

    def clean_acc(self):
        for p in self.points:
            p.clean_acc()
    
    def append(self, *args, **kwargs):
        self.points.append(Point(*args, **kwargs))
    
    def gather_coords(self):
        return [p.coords for p in self.points]

Частный случай. Перемещение частиц и визуализация векторного поля

Вот мы и дошли до самого интересного. Начнем с…

Моделирование движения частиц в электромагнитном поле

u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
for i in range(3):
    u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)

Вообще-то коэффициент k должен быть равен каким-то там миллиардам (9*10^(-9)), но так как он же будет гаситься временем t -> 0, я сразу решил сделать и то и другое адекватными числами. Поэтому в нашей физике k=300'000. А со всем остальным, думаю, понятно.

r ** 2 + 0.1

— это избежание деления на 0. Мы, конечно, могли бы заморочиться, решить большующую систему диффуров, но во-первых нет уравнения движения для более чем 2 тел, а во-вторых это явно уже не входит в понятие «статья для новичков»

Далее мы добавляем десять точек (2-мерного пространства) с координатами от 0 до 10 по каждой из осей. Также, мы даем каждой точке заряд от -0.25 до 0.25. Теперь сделаем цикл и нарисуем точки по их координата (и следы):


X, Y = [], []
for i in range(130):
    u.step(0.0006)
    xd, yd = zip(*u.gather_coords())
    X.extend(xd)
    Y.extend(yd)
plt.figure(figsize=[8, 8])
plt.scatter(X, Y)
plt.scatter(*zip(*u.gather_coords()), color="orange")
plt.show()

Что должно было получиться:

Элементарная симуляция кастомного физического взаимодействия на python + matplotlib - 6

На самом деле рисунок там будет совершенно рандомный, ведь траектория каждой точки непредсказуема на данный момент развития механики.

Визуализация векторного поля

Тут все просто. Нам нужно пройтись по координатам с каким-то шагом и нарисовать в каждых из них вектор в нужном направлении. 


fig = plt.figure(figsize=[5, 5])
res = []
STEP = 0.3
for x in np.arange(0, 10, STEP):
    for y in np.arange(0, 10, STEP):
        inten = u.intensity(Vector(x, y))
        F = inten.mod()
        inten /= inten.mod() * 4  # длина нашей палочки фиксирована
        res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F))
for r in res:
    plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) # Цвет по хитрой формуле чтобы добиться градиента
    
plt.show()

Примерно такой вывод должен был получиться.

Элементарная симуляция кастомного физического взаимодействия на python + matplotlib - 7

Можно удлинить сами векторы, заменим * 4 на * 1.5:

Элементарная симуляция кастомного физического взаимодействия на python + matplotlib - 8

Играем с мерностью и моделированием

Создадим пятимерное пространство с 200 точек.

u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1))
for i in range(200):
    u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)

Теперь все координаты, скорости и т. д. определены в пяти измерениях. Теперь что-нибудь помоделируем:

velmod = 0
velocities = []
for i in range(100):
    u.step(0.0005)
    velmod = sum([p.speed.mod() for p in u.points])   # Добавляем сумму модулей скоростей всех точек
    velocities.append(velmod)
plt.plot(velocities)
plt.show()

Элементарная симуляция кастомного физического взаимодействия на python + matplotlib - 9

Это — график суммы всех скоростей в каждый момент времени. Как видите, со временем они потихоньку ускоряются.

Ну вот это была коротенькая инструкция как сделать такую простую штуку. А вот что бывает, если поиграться с цветами:

Весь код с демо


import random

class Vector(list):
    def __init__(self, *el):
        for e in el:
            self.append(e)

    def __add__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] + other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self + other

    def __sub__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] - other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self - other

    def __mul__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] * other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self * other

    def __truediv__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] / other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self / other

    def __pow__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] ** other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self ** other

    def __mod__(self, other):
        return sum((self - other) ** 2) ** 0.5

    def mod(self):
        return self % Vector.emptyvec(len(self))

    def dim(self):
        return len(self)
    
    def __str__(self):
        if len(self) == 0:
            return "Empty"
        r = [str(i) for i in self]
        return "< " + " ".join(r) + " >"
    
    def _ipython_display_(self):
        print(str(self))

    @staticmethod
    def emptyvec(lens=2, n=0):
        return Vector(*[n for i in range(lens)])

    @staticmethod
    def randvec(dim):
        return Vector(*[random.random() for i in range(dim)])


class Point:
    def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties):
        self.coords = coords
        if speed is None:
            self.speed = Vector(*[0 for i in range(len(coords))])
        else:
            self.speed = speed
        self.acc = Vector(*[0 for i in range(len(coords))])
        self.mass = mass
        self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
        self.q = q
        for prop in properties:
            setattr(self, prop, properties[prop])

    def move(self, dt):
        self.coords = self.coords + self.speed * dt

    def accelerate(self, dt):
        self.speed = self.speed + self.acc * dt

    def accinc(self, force):
        self.acc = self.acc + force / self.mass
    
    def clean_acc(self):
        self.acc = self.acc * 0
    
    def __str__(self):
        r = ["Point {"]
        for p in self.__params__:
            r.append("  " + p + " = " + str(getattr(self, p)))
        r += ["}"]
        return "n".join(r)

    def _ipython_display_(self):
        print(str(self))


class InteractionField:
    def __init__(self, F):
        self.points = []
        self.F = F

    def move_all(self, dt):
        for p in self.points:
            p.move(dt)

    def intensity(self, coord):
        proj = Vector(*[0 for i in range(coord.dim())])
        single_point = Point(Vector(), mass=1.0, q=1.0)
        for p in self.points:
            if coord % p.coords < 10 ** (-10):
                continue
            d = p.coords % coord
            fmod = self.F(single_point, p, d) * (-1)
            proj = proj + (coord - p.coords) / d * fmod
        return proj

    def step(self, dt):
        self.clean_acc()
        for p in self.points:
            p.accinc(self.intensity(p.coords) * p.q)
            p.accelerate(dt)
            p.move(dt)

    def clean_acc(self):
        for p in self.points:
            p.clean_acc()
    
    def append(self, *args, **kwargs):
        self.points.append(Point(*args, **kwargs))
    
    def gather_coords(self):
        return [p.coords for p in self.points]
 

# ДЕМО
 

import matplotlib.pyplot as plt
import numpy as np
import time


# Моделирование частиц со следами
if False:
    u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
    for i in range(10):
        u.append(Vector.randvec(2) * 10, q=(random.random() - 0.5) / 2)
    X, Y = [], []
    for i in range(130):
        u.step(0.0006)
        xd, yd = zip(*u.gather_coords())
        X.extend(xd)
        Y.extend(yd)
    plt.figure(figsize=[8, 8])
    plt.scatter(X, Y)
    plt.scatter(*zip(*u.gather_coords()), color="orange")
    plt.show()

def sigm(x):
    return 1 / (1 + 1.10 ** (-x/1000))



# Визуализация векторного поля
if False:
    u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
    for i in range(3):
        u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)
    fig = plt.figure(figsize=[5, 5])
    res = []
    STEP = 0.3
    for x in np.arange(0, 10, STEP):
        for y in np.arange(0, 10, STEP):
            inten = u.intensity(Vector(x, y))
            F = inten.mod()
            inten /= inten.mod() * 1.5
            res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F))

    for r in res:
        plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2]))))
        
    plt.show()



# Подсчет скоростей в 5-мерном пространстве
if False:
    u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1))
    for i in range(200):
        u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)
    velmod = 0
    velocities = []
    for i in range(100):
        u.step(0.0005)
        velmod = sum([p.speed.mod() for p in u.points])
        velocities.append(velmod)
    plt.plot(velocities)
    plt.show()

Следующая статья будет возможно о более сложном моделировании, а быть может и флюидах и уравнениях Навье-Стокса.

Автор: WhiteBlackGoose

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js