В материале, первую часть перевода которого мы публикуем сегодня, речь пойдёт о том, как JavaScript-движок V8 выбирает оптимальные способы представления различных JS-значений в памяти, и о том, как это влияет на внутренние механизмы V8, касающиеся работы с так называемыми формами объектов (Shape). Всё это поможет нам разобраться с сутью недавней проблемы, касающейся производительности React.
Типы данных в JavaScript
Каждое JavaScript-значение может иметь только один из ныне существующих восьми типов данных: Number, String, Symbol, BigInt, Boolean, Undefined, Null и Object.
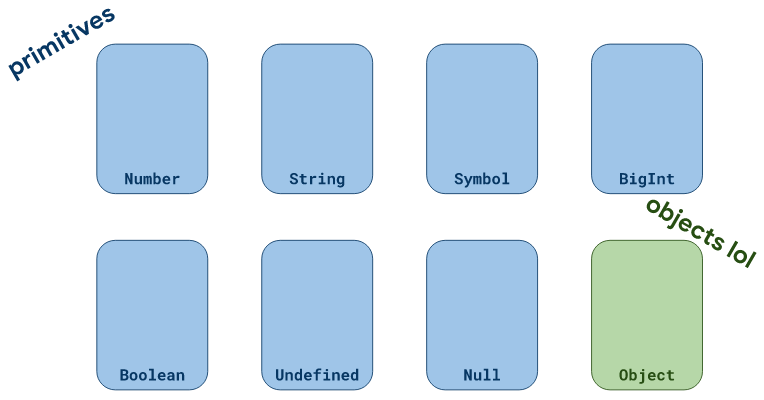
Типы данных в JavaScript
Тип значения можно выяснить с помощью оператора typeof, но тут имеется одно важное исключение:
typeof 42;
// 'number'
typeof 'foo';
// 'string'
typeof Symbol('bar');
// 'symbol'
typeof 42n;
// 'bigint'
typeof true;
// 'boolean'
typeof undefined;
// 'undefined'
typeof null;
// 'object' - вот то исключение, о котором идёт речь
typeof { x: 42 };
// 'object'
Как видите, команда typeof null возвращает 'object', а не 'null', несмотря на то, что значение null имеет собственный тип — Null. Для того чтобы понять причину подобного поведения typeof, примем во внимание то, что множество всех JavaScript-типов может быть разделено на две группы:
- Объекты (то есть — тип
Object). - Примитивные значения (то есть — любые необъектные значения).
В свете этого знания оказывается, что null означает «отсутствие объектного значения», в то время как undefined — это «отсутствие значения».
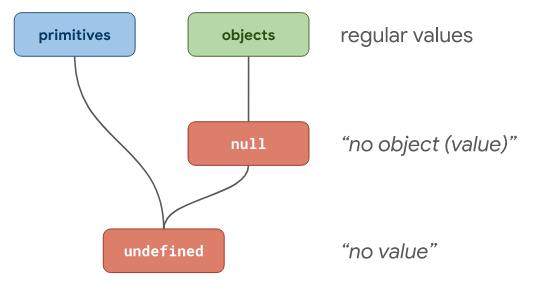
Примитивные значения, объекты, null и undefined
Следуя этим размышлениям в духе Java, Брендан Эйх спроектировал JavaScript так, чтобы оператор typeof возвращал бы 'object' для значений тех типов, которые расположены на предыдущем рисунке справа. Сюда попадают все объектные значения и null. Именно поэтому истинным является выражение typeof null === 'object' несмотря на то, что в спецификации языка имеется отдельный тип Null.
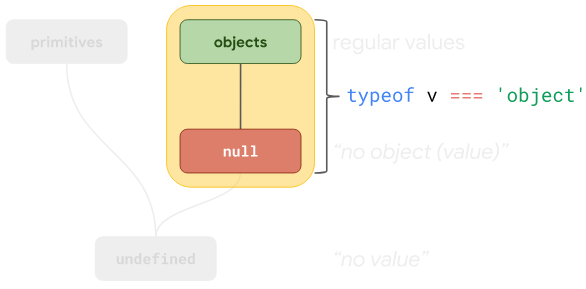
Выражение typeof v === 'object' истинно
Представление значений
JavaScript-движки должны иметь возможность представления любых JavaScript-значений в памяти. Однако важно отметить то, что типы значений в JavaScript отделены от того, как JS-движки представляют их в памяти.
Например, значение 42 в JavaScript имеет тип number.
typeof 42;
// 'number'Существует несколько способов представления в памяти целых чисел наподобие 42:
| Представление | Биты |
| 8 бит, с дополнением до двух | 0010 1010 |
| 32 бита, с дополнением до двух | 0000 0000 0000 0000 0000 0000 0010 1010 |
| Упакованное двоично-десятичное число (binary-coded decimal, BCD) | 0100 0010 |
| 32 бита, число с плавающей точкой IEEE-754 | 0100 0010 0010 1000 0000 0000 0000 0000 |
| 64 бита, число с плавающей точкой IEEE-754 | 0100 0000 0100 0101 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 |
В соответствии со стандартом ECMAScript числа — это 64-битные значения с плавающей точкой, известные как числа с плавающей точкой двойной точности (Float64). Однако это не означает того, что JavaScript-движки всегда хранят числа в представлении Float64. Это было бы очень и очень неэффективно! Движки могут использовать другие внутренние представления чисел — до тех пор, пока поведение значений в точности соответствует тому, как ведут себя Float64-числа.
Большинство чисел в реальных JS-приложениях, как оказалось, являются действительными индексами ECMAScript-массивов. То есть — целыми числами в диапазоне от 0 до 232-2.
array[0]; // Самый маленький из возможных индексов массива.
array[42];
array[2**32-2]; // Самый большой из возможных индексов массива.JavaScript-движки могут выбирать оптимальный формат для представления подобных значений в памяти. Делается это для того чтобы оптимизировать код, который работает с элементами массивов, используя индексы. Процессору, выполняющему операции обращения к памяти, нужно, чтобы индексы массива были бы доступны в виде чисел, хранящихся в представлении с дополнением до двух. Если вместо этого представлять индексы массивов в виде Float64-значений — это будет означать пустую трату системных ресурсов, так как движку тогда понадобилось бы преобразовывать Float64-числа в формат с дополнением до двух и обратно всякий раз, когда кто-то обращается к элементу массива.
Представление 32-битных чисел с дополнением до двух полезно не только для оптимизации работы с массивами. В целом можно отметить, что процессор выполняет целочисленные операции гораздо быстрее, чем операции, в которых используются значения с плавающей точкой. Именно поэтому в следующем примере первый цикл без проблем оказывается в два раза быстрее в сравнении со вторым циклом.
for (let i = 0; i < 1000; ++i) {
// быстро
}
for (let i = 0.1; i < 1000.1; ++i) {
// медленно
}То же самое применимо и к вычислениям с использованием математических операторов.
Например, производительность оператора взятия остатка от деления из следующего фрагмента кода зависит от того, какие числа участвуют в вычислениях.
const remainder = value % divisor;
// Быстро - если `value` и `divisor` представлены целыми числами,
// медленно в других случаях.
Если оба операнда представлены целыми числами, то процессор может вычислить результат весьма эффективно. В V8 есть дополнительная оптимизация для тех случаев, когда операнд divisor представлен числом, являющимся степенью двойки. Для значений, представленных в виде чисел с плавающей точкой, вычисления оказываются гораздо более сложными и занимают намного больше времени.
Так как целочисленные операции обычно выполняются гораздо быстрее операций над значениями с плавающей точкой, может показаться, что движки могут просто всегда хранить все целые числа и все результаты целочисленных операций в формате с дополнением до двух. К несчастью, такой подход означал бы нарушение спецификации ECMAScript. Как уже было сказано, в стандарте предусмотрено представление чисел в формате Float64, а некоторые операции с целыми числами могут приводить к появлению результатов в виде чисел с плавающей точкой. Важно, чтобы в подобных ситуациях JS-движки выдавали бы корректные результаты.
// Во Float64 имеется безопасный 53-битный целочисленный диапазон.
// Выход за пределы этого диапазона ведёт к потере точности.
2**53 === 2**53+1;
// true
// Float64 поддерживает отрицательные нули, в результате -1 * 0 должно дать -0, но
// в формате с дополнением до двух нет способа представления отрицательного нуля.
-1*0 === -0;
// true
// Float64 поддерживает значение Infinity, получить которое можно,
// разделив некое число на ноль.
1/0 === Infinity;
// true
-1/0 === -Infinity;
// true
// Float64 поддерживает и значения NaN.
0/0 === NaN;Даже хотя в предыдущем примере все числа, находящиеся в левой части выражений, являются целыми, все числа в правой части выражения являются значениями с плавающей точкой. Именно поэтому ни одна из предыдущих операций не может быть выполнена корректно с использованием 32-битного формата с дополнением до двух. JavaScript-движкам приходится уделять особое внимание тому, чтобы при выполнении целочисленных операций получались бы правильные (хотя и способные выглядеть необычно — как в предыдущем примере) Float64-результаты.
В случае с маленькими целыми числами, укладывающимися в диапазон 31-битного представления целых чисел со знаком, V8 использует особое представление, называемое Smi. Всё, что не является значением Smi, представляется в виде значения HeapObject, которое является адресом некоей сущности в памяти. Для чисел, не попадающих в диапазон Smi, у нас имеется особый вид HeapObject — так называемый HeapNumber.
-Infinity // HeapNumber
-(2**30)-1 // HeapNumber
-(2**30) // Smi
-42 // Smi
-0 // HeapNumber
0 // Smi
4.2 // HeapNumber
42 // Smi
2**30-1 // Smi
2**30 // HeapNumber
Infinity // HeapNumber
NaN // HeapNumber
Как видно из предыдущего примера, некоторые JS-числа представляются в виде Smi, а некоторые — в виде HeapNumber. Движок V8 оптимизирован в плане обработки Smi-чисел. Дело в том, что маленькие целые числа весьма часто встречаются в реальных JS-программах. При работе со Smi-значениями не нужно выделять память под отдельные сущности. Их использование, кроме того, позволяет выполнять быстрые операции с целыми числами.
Сравнение Smi, HeapNumber и MutableHeapNumber
Поговорим о том, как выглядит внутреннее устройство этих механизмов. Предположим, у нас имеется следующий объект:
const o = {
x: 42, // Smi
y: 4.2, // HeapNumber
};
Значение 42 свойства объекта x кодируется в виде Smi. Это значит, что оно может быть сохранено внутри самого объекта. Для хранения значения 4.2, с другой стороны, потребуется создание отдельной сущности. В объекте же будет ссылка на эту сущность.
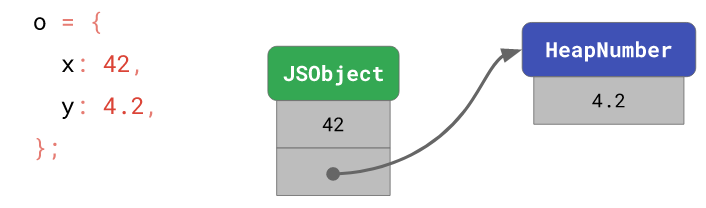
Хранение различных значений
Предположим, что мы выполняем следующий фрагмент JavaScript-кода:
o.x += 10;
// o.x теперь равняется 52
o.y += 1;
// o.y теперь равняется 5.2
В данном случае значение свойства x может быть обновлено в месте его хранения. Дело в том, что новое значение x равно 52, а это число укладывается в диапазон Smi.
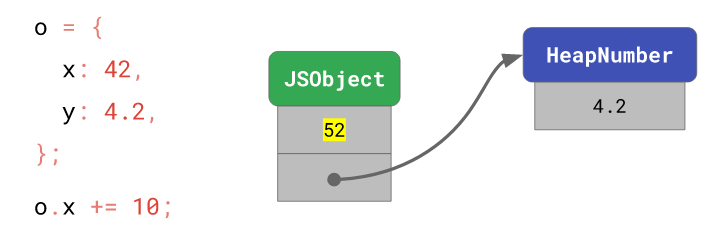
Новое значение свойства x сохраняется там же, где хранилось предыдущее значение
Однако новое значение y, 5.2, не укладывается в диапазон Smi, и оно, кроме того, отличается от предыдущего значения y — 4.2. В результате V8 приходится выделять память под новую сущность HeapNumber и ссылаться из объекта уже на неё.
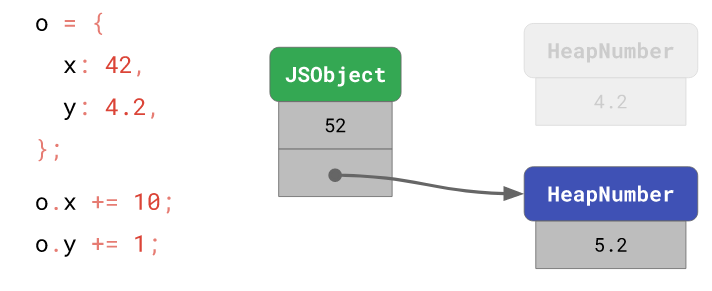
Новая сущность HeapNumber для хранения нового значения y
Сущности HeapNumber являются иммутабельными. Это позволяет реализовать некоторые оптимизации. Предположим, мы хотим присвоить свойству объекта x значение свойства y:
o.x = o.y;
// o.x теперь равно 5.2
При выполнении данной операции мы можем просто сослаться на ту же сущность HeapNumber, а не выделять дополнительную память для хранения одного и того же значения.
Один из недостатков иммутабельности сущностей HeapNuber заключается в том, что частое обновление полей, значения в которых выходят за пределы диапазона Smi, оказывается медленным. Это продемонстрировано в следующем примере:
// Создание экземпляра `HeapNumber`.
const o = { x: 0.1 };
for (let i = 0; i < 5; ++i) {
// Создание дополнительного экземпляра `HeapNumber`.
o.x += 1;
}
При обработке первой строки создаётся экземпляр HeapNumber, начальным значением которого является 0.1. В теле цикла это значение меняется на 1.1, 2.1, 3.1, 4.1, и наконец — на 5.1. В результате в процессе выполнения этого кода создаётся 6 экземпляров HeapNumber, пять из которых будут подвергнуты операции сборки мусора после завершения работы цикла.
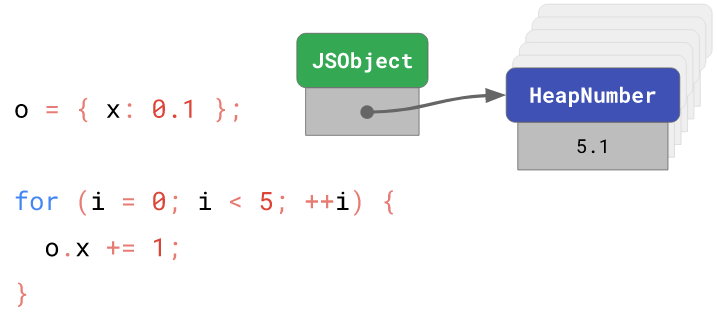
Сущности HeapNumber
Для того чтобы избежать этой проблемы в V8 имеется оптимизация, представляющая собой механизм обновления числовых полей, значения которых не укладываются в диапазон Smi, в тех же местах, где они уже хранятся. Если числовое поле хранит значения, для хранения которых сущность Smi не подходит, то V8, в форме объекта, помечает это поле как Double и выделяет память под сущность MutableHeapNumber, которая хранит реальное значение, представленное в формате Float64.
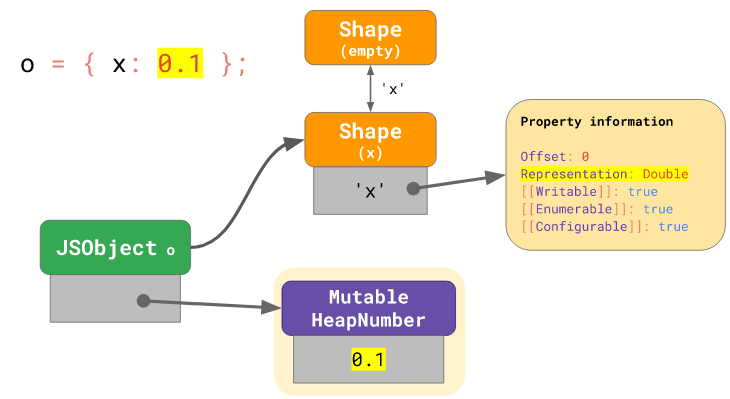
Использование сущностей MutableHeapNumber
В результате после того, как значение поля меняется, V8 больше не нужно выделять память под новую сущность HeapNumber. Вместо этого достаточно записать новое значение в уже имеющуюся сущность MutableHeapNumber.
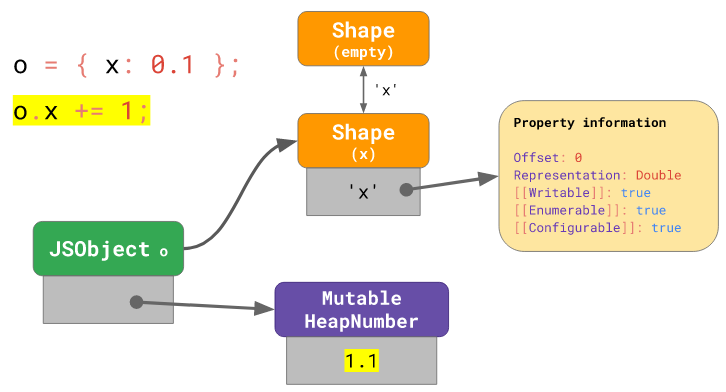
Запись нового значения в MutableHeapNumber
Однако и у этого подхода есть свои недостатки. А именно, так как значения MutableHeapNumber могут меняться — важно обеспечивать такую работу системы, при которой эти значения будут вести себя так, как это предусмотрено в спецификации языка.
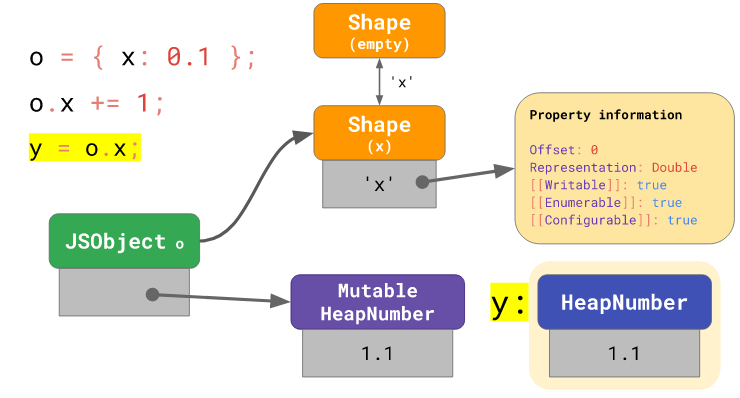
Недостатки MutableHeapNumber
Например, если присвоить значение o.x некоей другой переменной y, то нужно, чтобы значение y не изменялось бы при последующем изменении o.x. Это было бы нарушением спецификации JavaScript! В результате, когда осуществляется доступ к o.x, число, прежде чем оно будет присвоено y, должно быть переупаковано в обычное значение HeapNumber.
В случае с числами с плавающей точкой V8 выполняет вышеописанные операции упаковки с использованием своих внутренних механизмов. Но в случае с маленькими целыми числами использование MutableHeapNumber было бы пустой тратой времени из-за того, что Smi — это более эффективный способ представления таких чисел.
const object = { x: 1 };
// "Упаковка" свойства `x` объекта не выполняется
object.x += 1;
// обновление значения `x` внутри объекта
Для того чтобы избежать неэффективного использования системных ресурсов всё, что нам нужно сделать для работы с маленькими целыми числами, заключается в том, чтобы отмечать соответствующие им поля в формах объектов как Smi. В результате значения этих полей, до тех пор, пока они соответствуют диапазону Smi, можно обновлять прямо внутри объектов.
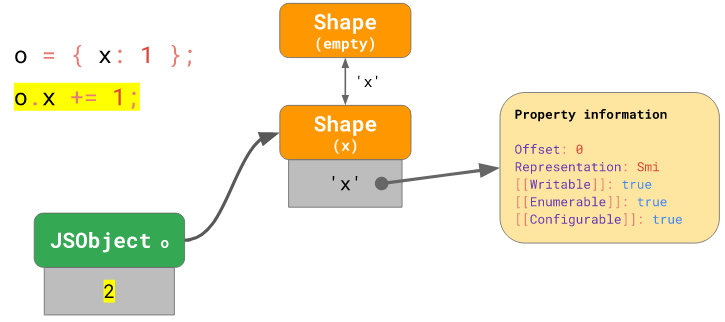
Работа с целыми числами, значения которых укладываются в диапазон Smi
Продолжение следует…
Уважаемые читатели! Сталкивались ли вы с проблемами производительности JavaScript-кода, вызванными особенностями JS-движков?
Автор: ru_vds








