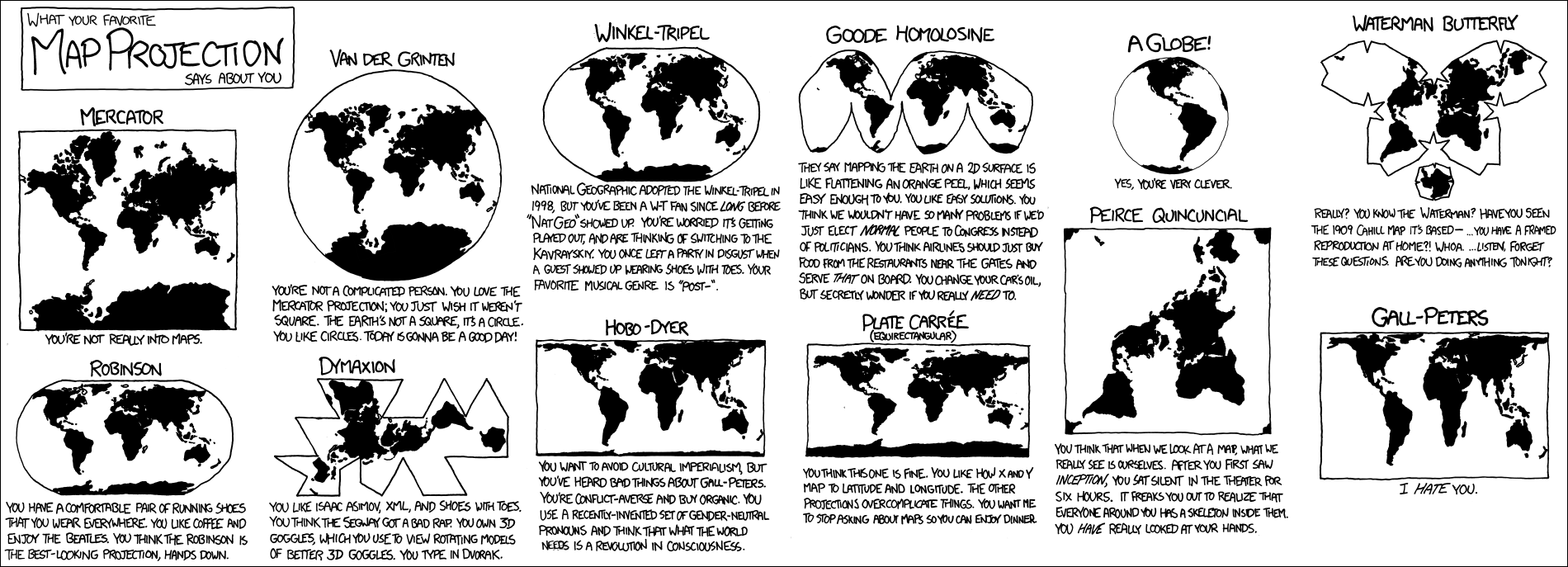
Xkcd — один из самых культовых веб-комиксов, и минималистичный стиль зарисовок будто из учебника механики стал его визитной карточкой. Автор комикса Рэндел Манро признавался, что старательно ищет вдохновение для новых выпусков: он пробует новые программы и игры, работает над математическими задачами, следит за новостями науки и технологий. Если бы он этого не делал, то комикс рассказывал бы о том, как художник сидит дома за компьютером.
Иногда выпуск комикса xkcd — это поверхностная шутка в узкой области знаний. Понять такой юмор сможет специалист или хотя бы слабо знакомый с затрагиваемой областью, а остальные будут лишь недоумевать. Пример такого выпуска — xkcd.com/977 Map Projections 2011 года. Для полного понимания выпуска нужно лишь примерно представлять историю и функцию различных проекций карт мира, иначе комикс останется чёрно-белым рисунком.
Даже внешне однозначные вопросы имеют несколько решений. Форма Земли — это похожий на шар геоид, но для удобства восприятия его лучше развернуть на плоскую карту. Сделать это можно несколькими способами. Каждый из них будет выполнен с различными компромиссами, поскольку искажения формы, углов или длин неизбежны. Какие-то проекции дают больше искажений, другие легче воспринимать, к каким-то мы просто привыкли.
Не все мы смотрим на карту для навигации в открытом море. Часто выбор метода преобразования формы Земли — это не вопрос жизни и смерти, это художественная иллюстрация. В этих случаях проекцию выбирают из устоявшихся вкусов и предпочтений — точно так же, как выбирают одежду или автомобиль. Можно смешно шутить про моду на дорогие кроссовки среди директоров крупных компаний Кремниевой долины или про популярность заниженных автомобилей. Точно так же шуткам поддаются предпочтения картографической проекции, как это и было сделано в Map Projections.
Разобьём комикс на несколько частей и рассмотрим их в удобном нам порядке.
Глобус!

Да, ты очень умный.
Земля — сложное тело с рельефом. Даже если принять её за шар, эллипсоид вращения или геоид, Землю всё равно не получится «сплющить» без искажений. Искажаются длины рек и дорог, площади и формы стран и материков, углы для навигации. Любая проекция — это компромисс между тем, какие искажения нежелательны.
Поэтому любая попытка представить Землю на плоскости без искажений обречена на провал, о чём напоминает этот вариант ответа. Зачем пытаться сделать невозможное? Легче всего на вопрос о любимой картографической проекции самодовольно выкрикнуть: «Глобус!»
Понятно, что это не проекция, а лишь попытка умничать. Манро указывает на это в подписи.
Равнопромежуточная проекция (Плате-Карре)

Тебе кажется, что эта подойдёт. Тебе нравится, как X и Y преобразуются в широту и долготу. Другие проекции всё усложняют. Ты хочешь, чтобы я от тебя отстал и дал спокойно поужинать.
Это одна из самых старых проекций карты мира — вероятно, её изобрёл Птолемей ещё до нашей эры. Геоид преобразуется в цилиндр и разворачивается на лист бумаги. Сохраняются расстояния вдоль экватора и всех меридианов, но углы и площадь искажаются. Такую проекцию удобно использовать в компьютерных геоинформационных системах: линейные координаты на проекции легко преобразуются в широту и долготу.
Равнопромежуточная проекция искажает углы и площади. Точки-полюсы на этой проекции растягиваются в линию. Из-за искажений равнопромежуточную проекцию не используют в навигации.
В представлении Манро такая проекция может понравиться занятому человеку, который не интересуется проекциями и связанными с ними премудростями.
Меркатор
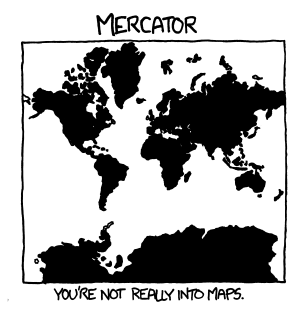
В картах ты разбираешься не очень.
В издании «Атласа» 1569 года фламандского картографа Герарда Меркатора на восемнадцати листах общим размером 202 на 124 сантиметра была представлена равноугольная цилиндрическая проекция. В названии заложены её характеристики: в каждой точке углы передаются без искажений, а параллели и меридианы сохраняют параллельность.
За это пришлось расплатиться искажениями масштаба: чем дальше объект уходит от экватора к полюсу, тем он крупнее. Сами полюса превращаются из точек в бесконечно большие объекты. Поэтому карта не простирается до полюсов, применяется отсечка по широтам в ±80°—85°.
Из-за этого не самая большая Антарктида приобретает в проекции Меркатора огромные размеры, а Африка и страны Южной и Юго-Восточной Азии кажутся меньше, чем на самом деле. На проекции Меркатора Гренландия выглядит размером с весь Африканский континент, хотя на деле её площадь меньше площади Демократической Республики Конго.
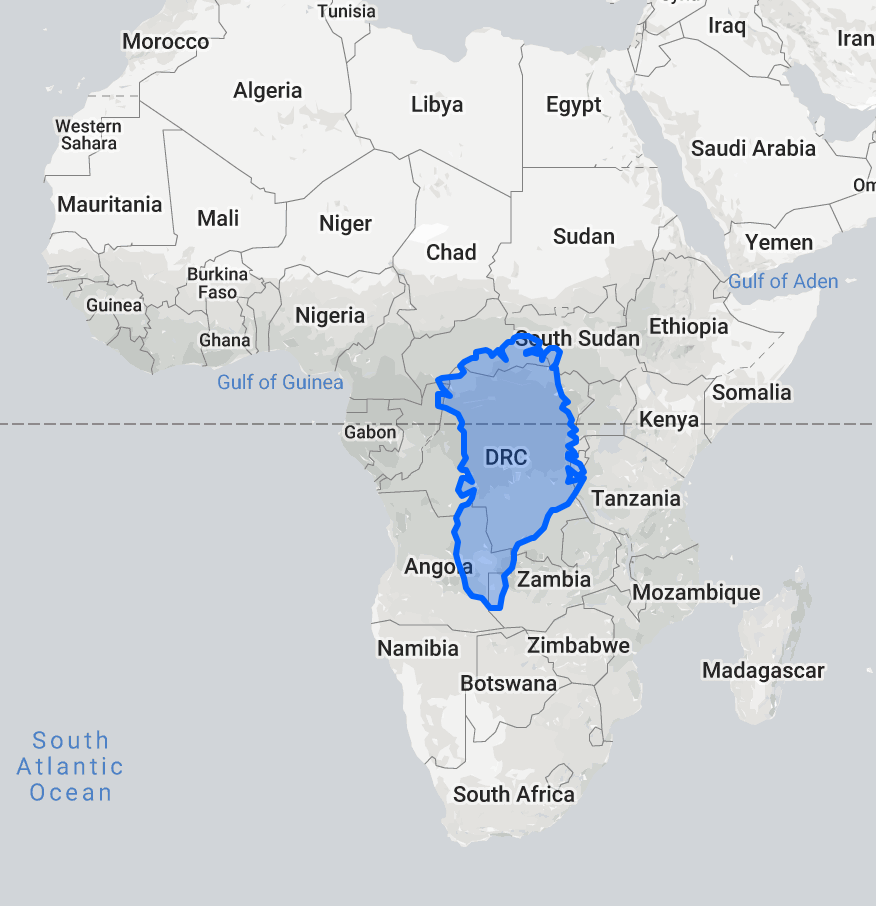
Сайт The True Size Of демонстрирует, насколько сильно проекция Меркатора искажает площади.
Но проекция Меркатора пригодилась для навигации мореплавателей и, впоследствии, воздушного движения. Если стрелка компаса сохраняет своё положение, то траектория движения корабля в проекции Меркатора будет изображаться прямой линией. Пересечение двух дорог сохранит свой угол и в этой проекции. Проекция Меркатора широко используется в навигации и по сей день.
Более того, проекция Меркатора хорошо сохраняет общие очертания объектов. Вариант такой проекции используют все основные картографические сервисы: Google Maps, Bing Maps, OpenStreetMap и так далее. Отличие «веб-Меркатора» заключается в в том, что за пределами широт в примерно ±85° используется другая проекция, которая не уходит в бесконечность в полюсах.
Задача картографической проекции решена, но не полностью. Да, ходить по морю по Меркатору очень удобно, но не получится изобразить два небольших участка вокруг полюсов. Площади и длины искажаются. Подобная проекция может понравиться только тому, кому безразличны проблемы картографии, намекает подпись.
Проекция Галла — Петерса

Я тебя ненавижу.
Обыватель привык к проекции Меркатора, которая нагло искажает реальные размеры стран вблизи экватора. Европа чуть ли не крупнее Южной Америки, хотя на деле она меньше почти в два раза. Гренландия на самом деле в 14 раз меньше Африки, хотя у Меркатора они выглядят примерно одинаково. Государства Европы и Северной Америки, выглядят крупнее, чем околоэкваториальные страны, что принижает важность последних. По крайней мере, примерно так звучит политически мотивированная критика проекции Меркатора.
В 1855 году шотландский священник Джеймс Галл описал проекцию, которая получила название «ортографическая проекция Галла». В этой проекции корректно отображаются площади объектов за счёт искажения их форм. На тот момент у проекции не было никаких политических подтекстов, это был побочный продукт астрономических наблюдений.
В 1967 году немец Арно Петерс создал идентичную проекцию, а в 1973 году, в период политического климата поиска социальной справедливости, представил её в виде нового изобретения. Проекция Петерса демонстрировалась как метод борьбы с империализмом и евроцентризмом. На проекции Меркатора Европа крупная и в центре, указывал автор, а на «новой» проекции Африка и близкие к экватору страны оказываются правильных размеров.
Само же название «проекция Галла — Петерса» впервые появилось в публикации Артура Робинсона 1986 года. Проекцию упоминают, к примеру, в телесериале «Западное крыло», который рассказывает о работе вымышленной администрации президента США. Сюжет подразумевает, что картографы предложили поменять карты в школах на «более социально справедливые».
Проблема проекции Галла — Петерса состоит в изначальном допущении о том, что проекция Меркатора ставит своей — основной или побочной — целью подъём значимости европейских государств за счёт их укрупнения на карте мира. На самом деле проекция Меркатора лишь удобна для морской навигации, также она не искажает локальные формы объектов.
Проекция Галла — Петерса сохраняет площади за счёт искажения углов, расстояний и формы объектов. Искажения значительны, хотя Петерс это отрицал. Несмотря на утверждения об обратном, проекция Петерса не представляет мир в том виде, в котором он выглядит на самом деле.
Самое забавное — это то, что эта карта наоборот изображает бедные страны у экватора с искажениями. Дело в том, что на этой проекции на 45 градусах северной и южной широты форма объектов не меняется относительно реальных. Чем дальше от этих двух линий, тем больше искажения формы. Одна из двух линий без искажений заходит на Европу — то есть тот район мира, от влияния которого проекция Галла — Петерса так стремится нас избавить. То есть наиболее сильно у Петерса искажается Африка, хотя богатые «страны-империалисты» (Европа, США, Япония, Австралия) почти не меняют реальную форму.
Для сравнения: у проекции Бермана линия без искажений проходит на 30 градусах, у равновеликой цилиндрической проекции Ламберта — на экваторе.
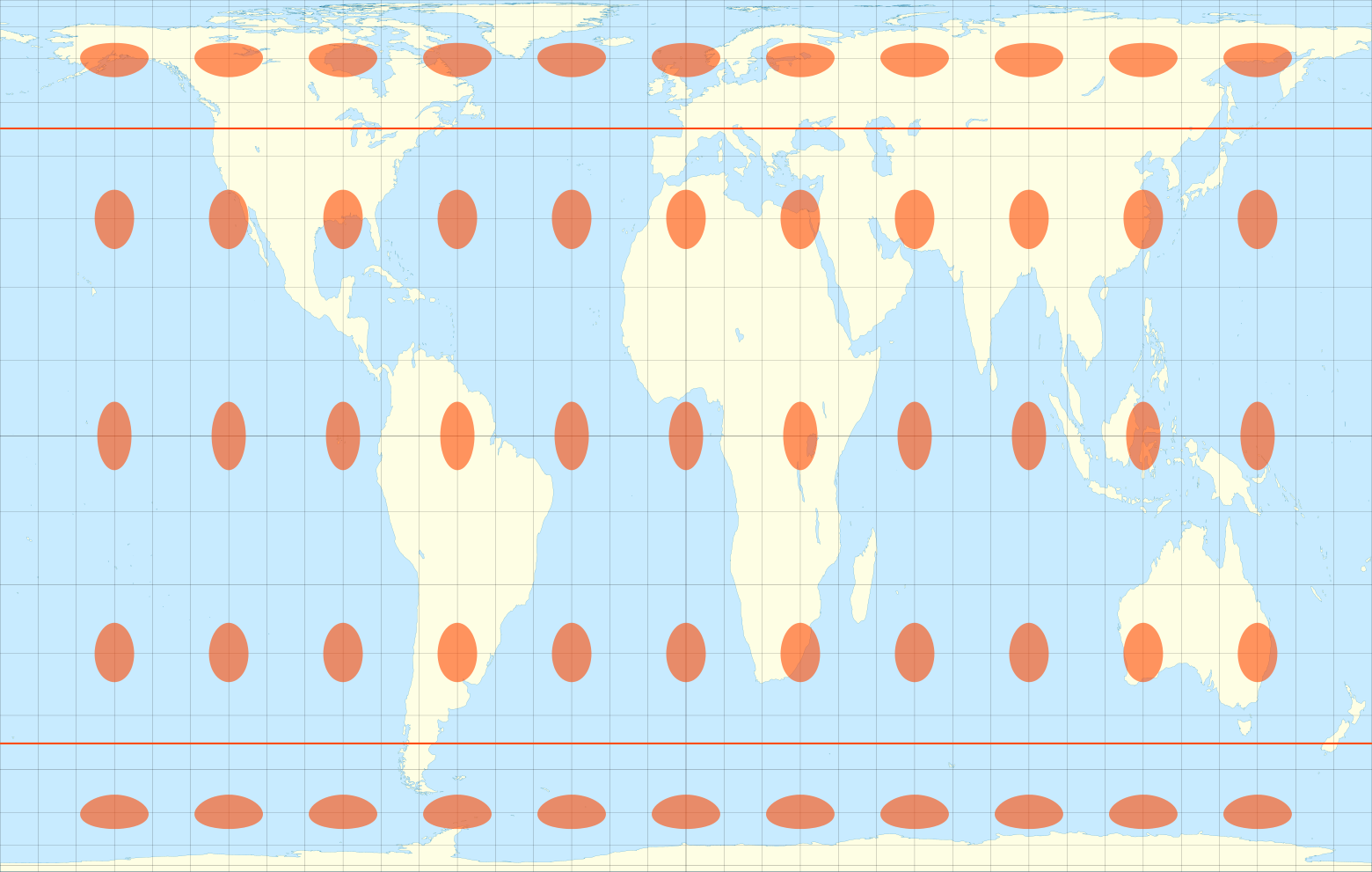
Эллипсы искажения на проекции Галла — Петерса
Карта в проекции Галла — Петерса прямоугольная, что немного странно для проекции в XX веке. До проекции Петерса уже существовали проекции с сохранением масштаба, хотя карту представили как нечто до этого невиданное. Наконец, если допустить, что чем больше страна, тем она воспринимается могущественней, то наиболее важной в проекции Меркатора будет Антарктида.
Если подытожить, то проекция Галла — Петерса находит проблему, которой не существует, не может её решить, но допускает множество новых искажений. Тем не менее, у неё находятся сторонники, которые искренне верят, что проекция Меркатора должна уйти в прошлое. К примеру, эту проекцию используют ЮНЕСКО, некоторые британские школы и часть школ штата Массачусетс.
Манро не ограничивается коротким замечанием, что ненавидит тех, у кого эта проекция любимая. Также в альт-тексте комикса он спрятал послание с шуткой в стиле Горацио Кейна: «Чего? Думаешь, мне не нравится карта Петерса, потому что вызов моим культурным допущениям вызывает у меня дискомфорт? А ты не думаешь, что сам не :: надевает очки:: проецируешь?»
Проекция Хобо — Дайера
Ты хочешь избежать культурного империализма, но про Галла — Петерса ты слышал плохое. Ты неконфликтный и покупаешь органические продукты. Ты используешь недавно изобретённый набор гендерно-нейтральных местоимений и считаешь, что миру нужна революция в самосознании.
В названии проекции Хобо — Дайера закодировано сразу три имени: Ховарда Бронстейна и Боба Абрамаса, менеджеров заказавшей проекцию компании ODT Maps, а также картографа Мика Дайера, который выполнил заказ. Она была создана в 2002 году как более приятный для глаза вариант Галла — Петерса.
Карта всё так же искажает формы стран. На 37,5° северной и южной широты искажений нет.
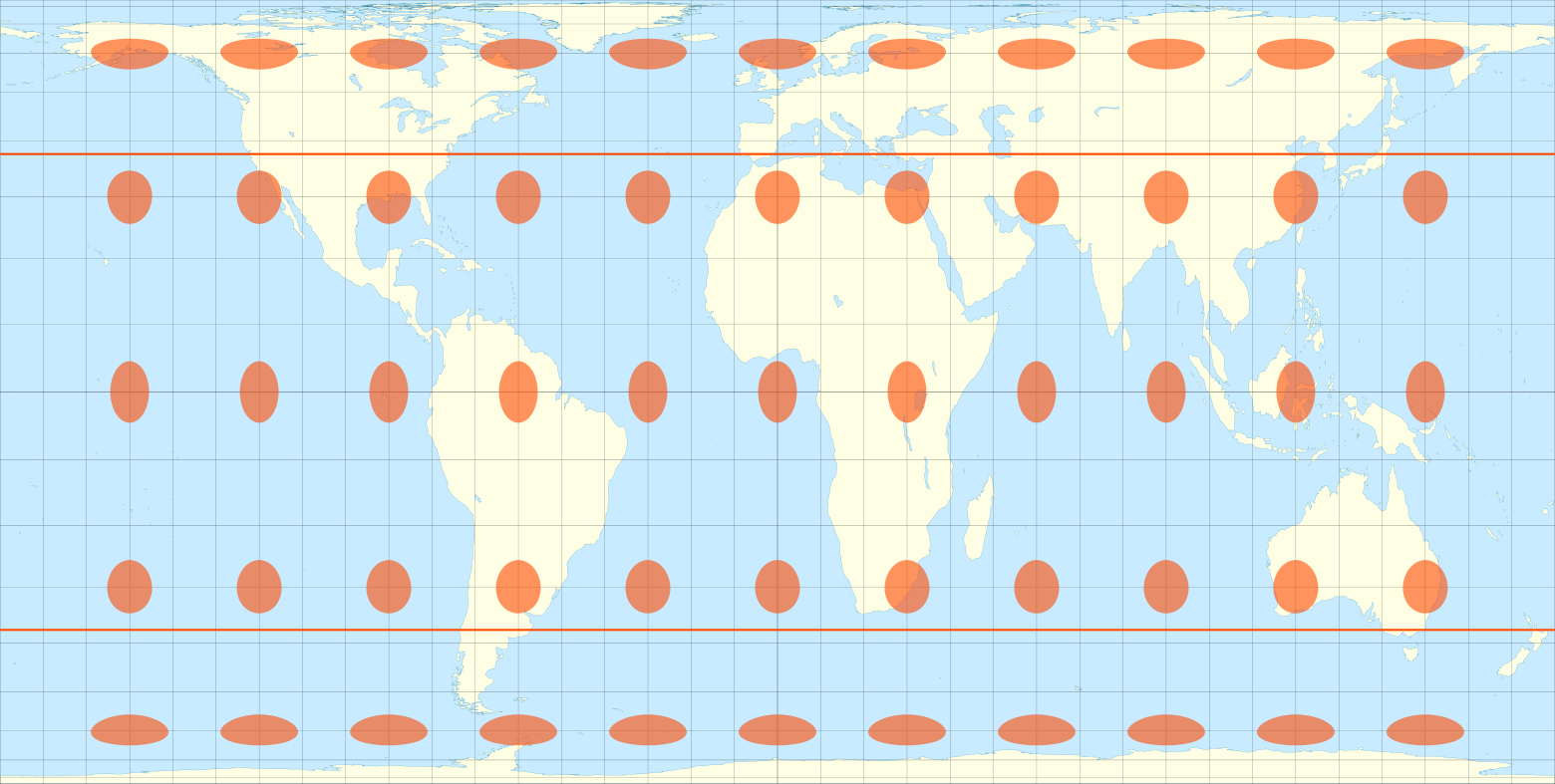
Эллипсы искажения на проекции Хобо — Дайера
Манро обыгрывает историю проекции, указав, что её любитель может оказаться менее радикальным и более неконфликтным сторонником социальной справедливости и заботы об окружающей среде. Такой человек покупает органические продукты, то есть выращенные с минимальным использованием синтетических удобрений, пестицидов и гербицидов. Он использует гендерно-нейтральные местоимения, чтобы никого не обидеть.
Перевёрнутая карта мира в проекции Хобо — Дайера
Проекция Пирса
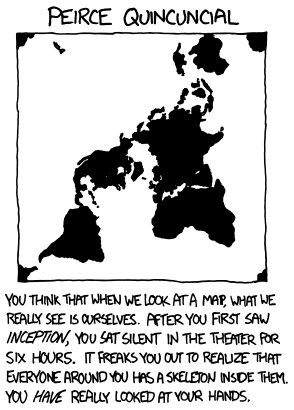
Ты считаешь, что когда мы смотрим на карту, на самом деле мы видим себя. После первого просмотра фильма „Начало“ ты шесть часов молча сидел в кинотеатре. Тебя пугает то, что внутри каждого из окружающих находится скелет. Однажды ты по-настоящему всмотрелся в свои руки.
Планета в проекции Пирса развёрнута так, что из проекции можно составить бесконечный узор. Она корректно передаёт углы во многих местах за исключением областей, где экватор и меридианы внезапно меняют направления. Экватор в проекции Пирса выглядит как квадрат, хотя у реального экватора острых углов нет. Сам Пирс утверждал, что искажённые области на карте занимают места меньше, чем у Меркатора.

Узор из Земли в проекции Пирса
У карт в проекции Пирса нет значимых практических применений. Зато сам алгоритм проекции удобен для представления на плоскости 360-градусных изображений — Пирс хорошо развернул сферу в квадрат.
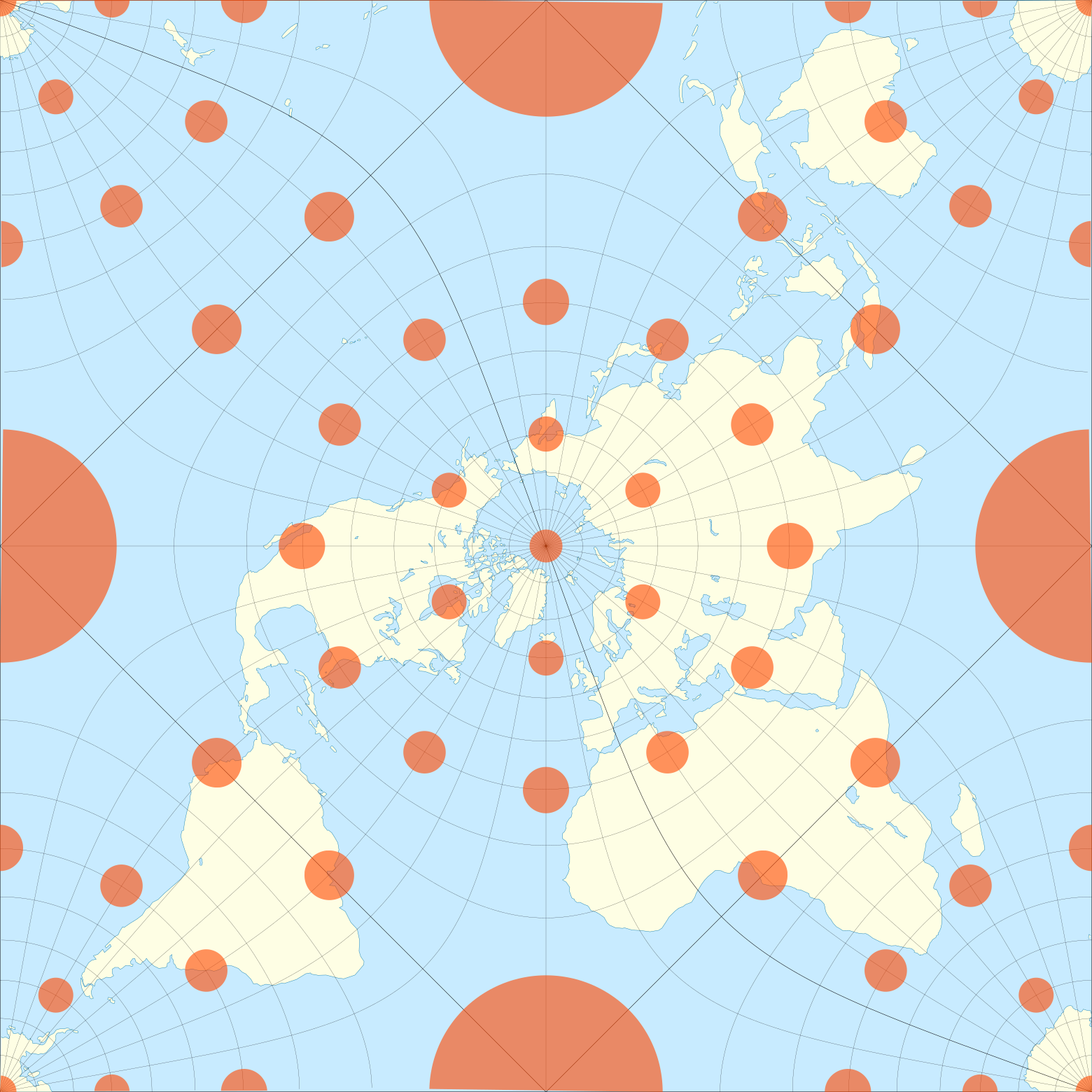
Эллипсы искажения на проекции Пирса
Сюжет фильма «Начало» использует сложную вложенную структуру, поэтому зрителю может потребоваться несколько просмотров для полного осмысления кинокартины. При правильном настрое психики может казаться странным наличие в теле скелета или сложность кисти человеческой руки. Вероятно, Манро намекает, что бесконечный узор из проекций Земли и квадратность экватора нравятся людям, которые склоны фиксироваться на мелких деталях.
Проекция Ван дер Гринтена
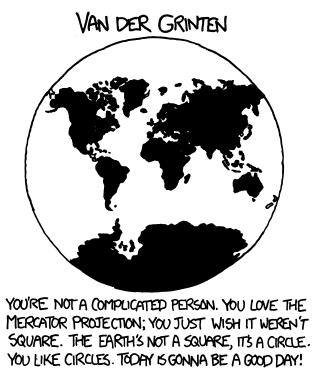
Ты человек несложный. Тебе нравится проекция Меркатора; тебе лишь хочется, чтобы она не была квадратной. Земля не квадратная, она круглая. Круги тебе нравятся. Сегодня будет отличный день!
В 1922 году Национальное картографическое общество США приняло в качестве стандартной карты мира проекцию Ван дер Гринтена. В этом статусе она просуществовала до 1988 года.
Эта проекция ни равновеликая, ни равноугольная. Она проектирует поверхность Земли в произвольную фигуру — круг. Она сохраняет знакомые по проекции Меркатора очертания материков и стран, незначительно убирая искажения. При этом в полюсах искажение огромно — Антарктида будто крупнее всей остальной суши.
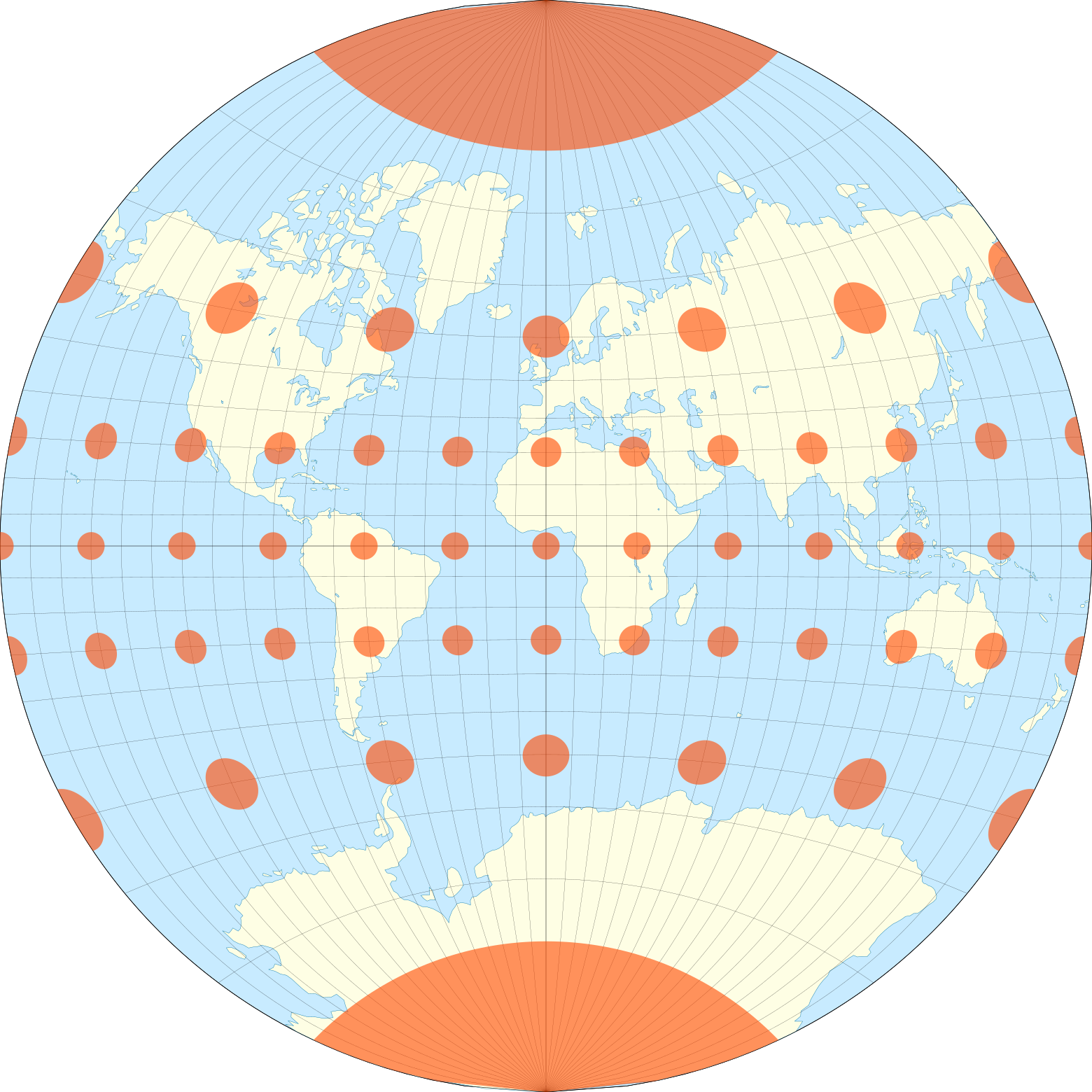
Эллипсы искажения проекции Ван дер Гринтена
Манро представляет поклонника такой проекции в виде откровенно глупого и наивного человека. Сфера и круг имеют мало общего, но для любителя Ван дер Гринтена это одно и то же. На самом деле этот человек недалеко отошёл от проекции Меркатора, намекает Манро.
Проекция Робинсона
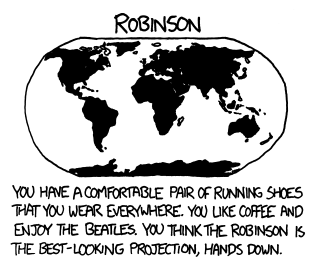
У тебя есть удобная пара беговых кроссовок, которую ты носишь везде. Тебе нравится кофе и «Битлз». Ты считаешь, что проекция Робинсона — без вопросов лучшая.
Творение Робинсона сменило Ван дер Гринтена на посту проекции стандартной карты мира Национального картографического общества США в 1988 году. Десятилетие спустя, в 1998 году, проекцию сменили. Не исключено, что и сам автор комикса учил географию с картой такой проекции.
Проекция Робинсона — это тоже ни равноугольная, ни равновеликая проекция, а компромисс. Меридианы нежно загибаются, а полюса вытягиваются в ниточки. Поэтому на полюсах искажения огромны, но уже при небольшом отходе в сторону экватора ошибки не так значительны. Это во многом художественная картина мира: проекция задаётся таблицей значений с шагом в 5 градусов, а не формулой. Остальные значения получаются приближением.
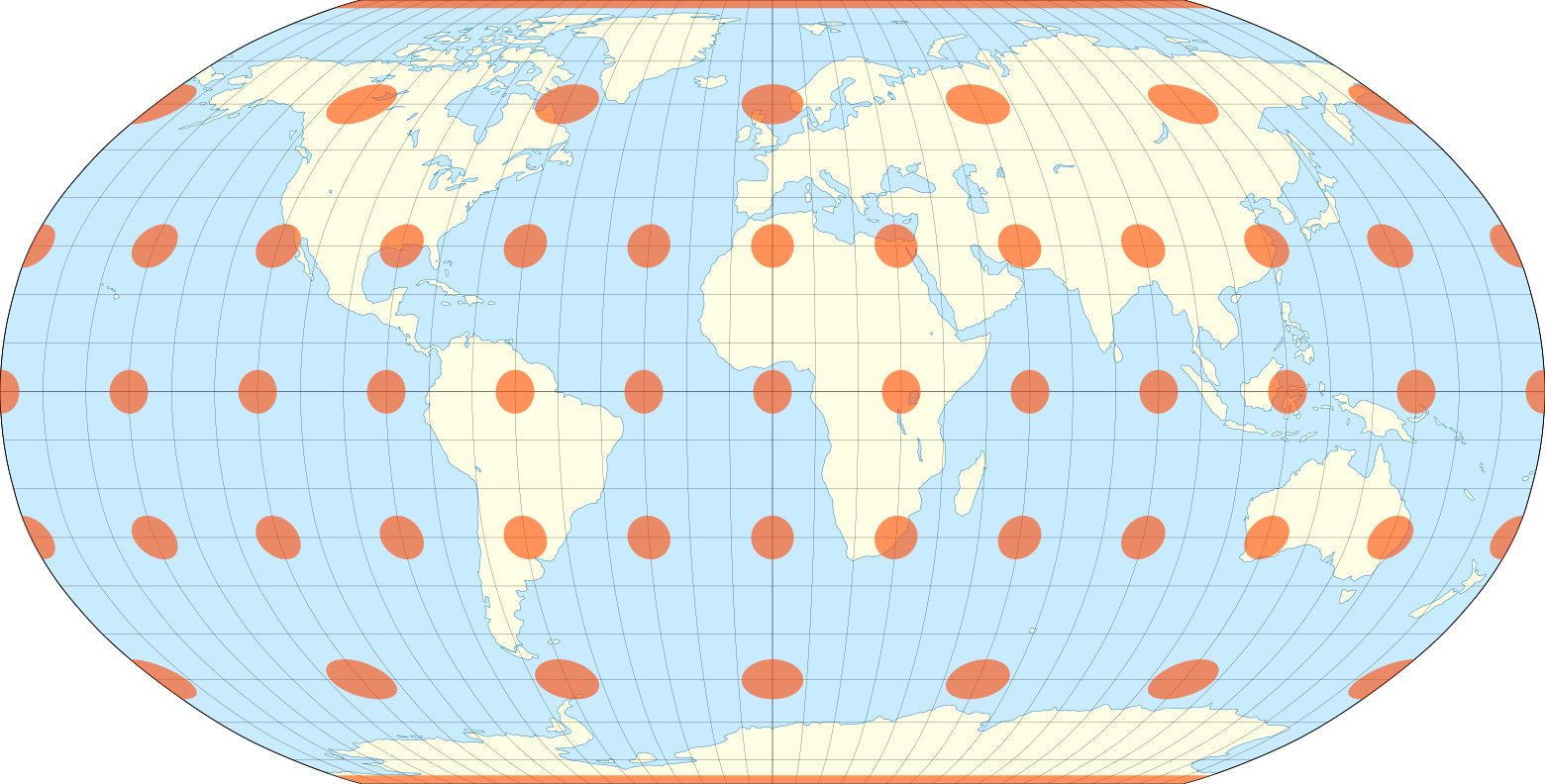
Эллипсы искажения проекции Робинсона.
Манро намекает, что эта проекция привычна и приятна: он ассоциирует её поклонника с мягкими и комфортными вещами. Музыкальные вкусы людей фиксируются в подростковом возрасте. Возможно, Манро указывает, что такой человек вырос в эпоху популярности «Битлз», то есть это любящий спокойную жизнь человек за сорок.
Тройная проекция Винкеля

Национальное картографическое общество приняло тройную проекцию Винкеля в 1998 году, но ты её обожал задолго до этого признания. Ты беспокоишься, что это конец, и подумываешь перейти на Каврайского. Однажды ты в отвращении покинул вечеринку, когда гость пришёл в обуви с пальцами. Название твоего любимого музыкального жанра начинается с „пост-“.
Тройная проекция Винкеля была опубликована в 1921 году, а в 1998 году Национальное картографическое общество приняло её в качестве стандартной. Это среднее арифметическое между равнопромежуточной проекцией и проекцией Айтофа — так картограф Освальд Винкель в своей компромиссной проекции попытался уменьшить все три типа искажений.
Популярный шуточный стереотип утверждает, что если некий продукт приобретает популярность, хипстеры немедленно отказываются от его употребления. Манро указывает, что поклонник тройной проекции Винкеля принадлежит к данной субкультуре. Такой человек откажется от неё в пользу неиспользуемой на Западе проекции советского геодезиста и картографа Каврайского, которая в целом похожа на тройную проекцию Винкеля.
Димаксион
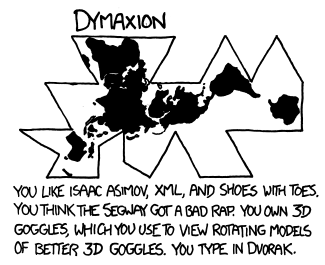
Тебе нравится Айзек Азимов, XML и ботинки с пальцами. Ты считаешь, что у сегвеев просто плохая репутация. У тебя есть 3D-очки, в которых ты разглядываешь вращающиеся модели 3D-очков получше. Твоя раскладка — Дворак.
Зачем обязательно мучиться с шаром? Нашу планету можно приближённо представить в виде многогранника, а его развёртку сделать картографической проекцией. Эту идею Бакминстер Фуллер опубликовал в журнале Life в 1943 году.
У этой развёртки есть несколько преимуществ. Искажения размеров и формы объектов меньше, чем на проекции Меркатора или Галла — Петерса. На такой карте удобно иллюстрировать научную теорию о миграции людей.
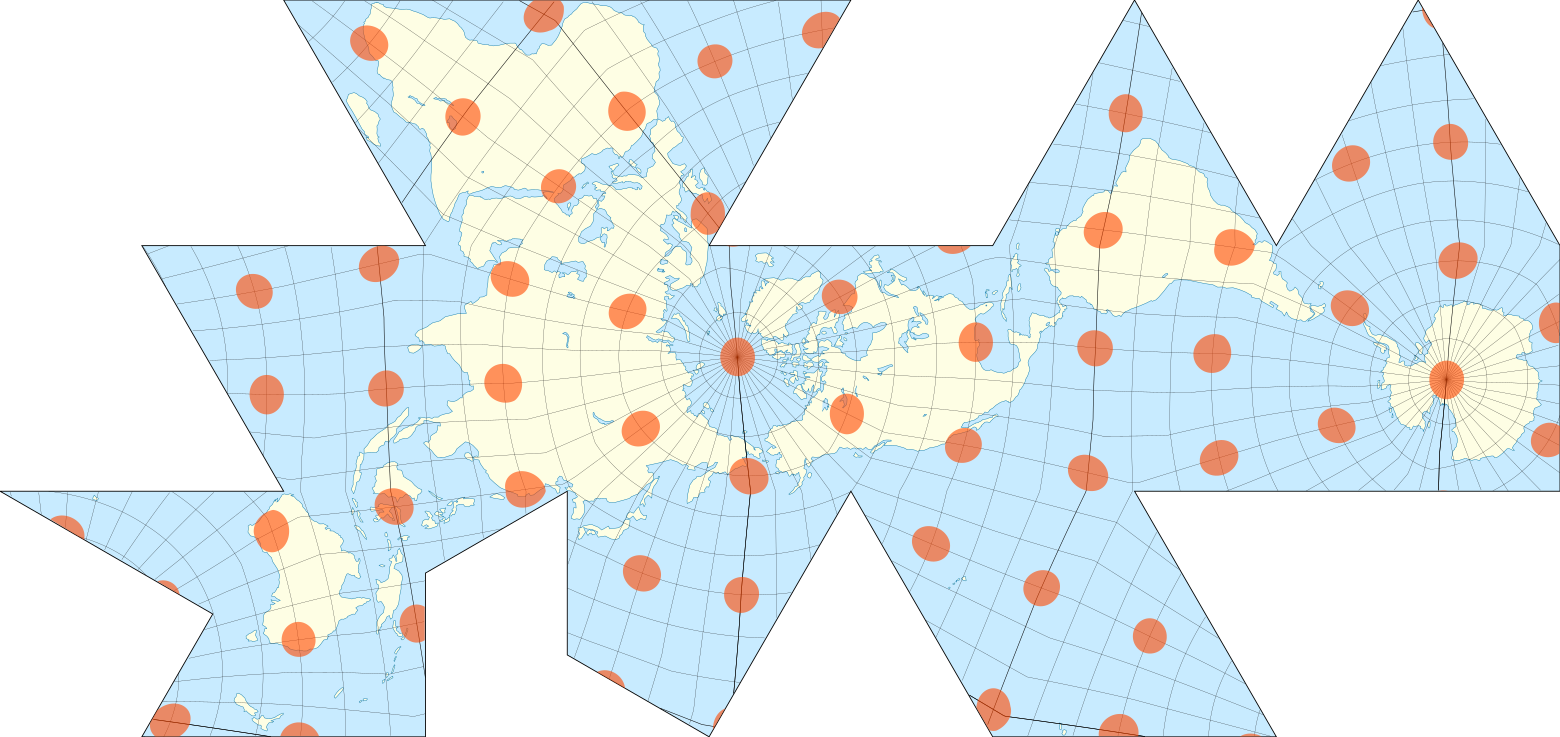
Эллипсы искажения проекции Димаксион
Вместе с тем нужно свыкнуться с несколькими новыми концепциями. На карте нет «верха» или «низа». Фуллер утверждал, что у Вселенной «север» и «юг» отсутствуют — есть только «внутри» и «снаружи». В проекции Димаксион трудно находить координаты объектов и указывать стороны света. Трудно находить пути для путешествий, они выглядят непредсказуемо.
Какими бы минимальными ни были искажения, но карты Земли нужны для передвижения по свету. Несмотря на оригинальность и красоту задумки, проекция Фуллера не получила какого-либо практического применения.
В подписи Манро собрал похожие случаи, когда внешне интересные изобретения на практике не имели значительного распространения, оставаясь чем-то нишевым. В списке не самый популярный язык разметки XML, необычная обувь с пальцами, дорогие и оттого непопулярные мобильные скутеры фирмы Segway. Для 3D-очков (то есть ранних шлемов виртуальной реальности) Манро намекает на отсутствие контента и приложений — это справедливо для начала 2010-х годов. Раскладка Дворака призвана ускорить набор текста относительно машинописной QWERTY, но требует полного переучивания и не демонстрирует настолько значительных преимуществ на практике.
«Бабочка Уотермана»
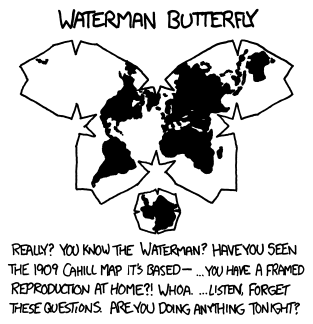
Серьёзно? Ты знаешь Уотермана? А что насчёт карты Кахилла 1909 года, на которой она основана… у тебя есть репродукция в рамке дома?! Ого… слушай, забудь про вопросы. Какие у тебя планы на вечер?!
Проекция Уотермана похожа на Димаксион: геоид примерно подобен многограннику, в данном случае — октаэдру. Затем многогранник разворачивают на плоскость. Как и в предыдущих случаях, форма объектов и их истинный размер искажаются не так сильно. Но на такой карте сложно указать стороны света и построить путь.
Уотерман опубликовал свою «бабочку» в 1996 году. Как напоминает Манро, она базировалась на работе Кахилла 1909 года. Архитектор Кахилл тоже покрошил Антарктиду на дольки, но делал это физически: он создал и запатентовал раскладной резиновый глобус, а потом сплющивал его.

Как и в случае с Димаксионом, эта проекция не получила значимого практического применения. Знать про неё может лишь большой поклонник картографии. Манро шутит, что ему есть о чём поболтать с человеком, который называет «бабочку Уотермана» своей любимой проекцией.
Проекция Гуда

Говорят, перенос Земли на двумерную плоскость — это как расплющить кожуру апельсина, что для тебя звучит просто. Ты любишь простые решения. Ты считаешь, что проблем у нас было бы меньше, выбирай мы в Конгресс нормальных людей вместо политиков. Ты считаешь, что авиалиниям стоило бы просто закупать еду из ресторанов поблизости терминалов и подавать её на борту. Ты меняешь масло в своей машине, но втайне задумываешься, а нужно ли.
В 1923 году Джон Гуд разработал свою псевдоцилиндрическую равновеликую замену проекции Меркатора. Проекция Гуда были призвана корректно передавать площади объектов. У проекции есть несколько разрывов по океанам и Антарктиде, которые выполнены для уменьшения искажений.
На некоторых вариантах проекции Гуда объекты повторяются. Можно выполнить такую проекцию с упором на океан.
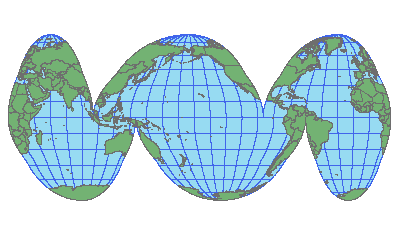
Основной недостаток проекции Гуда — огромные промежутки в океанах, которые не позволяют визуально оценить расстояние между материками. Проекция Гуда призвана сохранять площади и выполняет это для материков. Но океаны в ней выглядят больше, чем на самом деле.
Действительно, за этой проекцией закрепилось сравнение с кожурой апельсина. Манро считает желание развернуть глобус в кожуру чрезмерно простым и неосведомлённым подходом к трудной проблеме, какой является картография. Он приводит в пример выборы в парламент: «нормальные» люди вряд ли бы смогли пробиться в строго выраженный правящий класс США. Да и в конечном итоге это вряд ли бы разрешило проблемы страны. К тому же, кто определяет «нормальность» человека?
Восприятие вкуса сильно зависит от состава воздуха и давления, а обычный ресторан вряд ли может единовременно заготовить нужные количества еды. Также она должна быть упакована специальным образом. Если заставить какой-то ресторан учесть все эти требования и поменять свои технологии, то он превратится в поставщика еды для пассажиров самолётов.
Производитель автомобиля указывает, когда менять масло. Наш любитель проекции Гуда иногда размышляет, а нет ли между автопроизводителями и продавцами автомобильного масла сговора.
Всё это — ловушки, в которые можно попасть, если недооценить решаемую проблему. Манро указывает, что и разворот геоида на плоскость не так прост, как кажется поклоннику проекции Гуда.
По материалам Brilliant Maps, обсуждения на «Реддите» и Explain xkcd.
Автор: atomlib