Каждый в IT-индустрии знает, насколько сложно оценить срок выполнения проекта. Трудно объективно оценить, сколько времени займёт решение трудной задачи. Одна из моих любимых теорий заключается в том, что здесь имеет место просто статистический артефакт.
Предположим, вы оцениваете проект в 1 неделю. Предположим, есть три одинаково вероятных результата: либо он займёт 1/2 недели, либо 1 неделю, либо 2 недели. Медианный результат фактически такой же, как и оценка: 1 неделя, но среднее значение (aka average, aka expected value) составляет 7/6 = 1,17 недель. Оценка фактически откалибрована (беспристрастна) для медианы (которая равна 1), но не для среднего.
Разумной моделью для «фактора инфляции» (фактическое время, разделённое на оценочное время) будет что-то вроде логнормального распределения. Если оценка равна одной неделе, то смоделируем реальный результат как случайную величину, распределённую в соответствии с логнормальным распределением около одной недели. В такой ситуации медиана распределения составляет ровно одну неделю, но среднее значение намного больше:
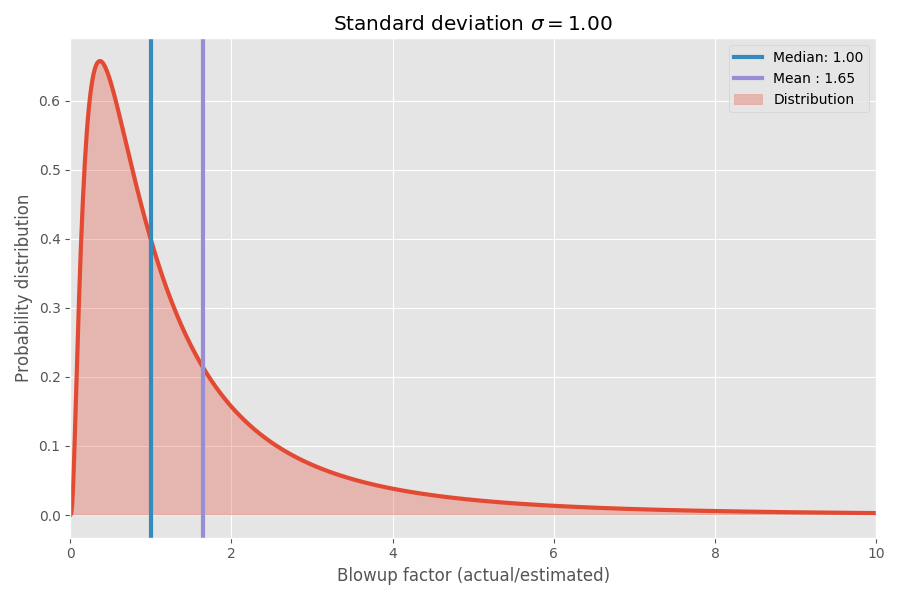
Если взять логарифм коэффициента инфляции, мы получим простое нормальное распределение с центром около 0. Это предполагает медианный коэффициент инфляции 1x, и, как вы, надеюсь, помните, log(1) = 0. Однако в различных задачах могут быть разные неопределённости вокруг 0. Мы можем моделировать их путём изменения параметра σ, который соответствует стандартному отклонению нормального распределения:
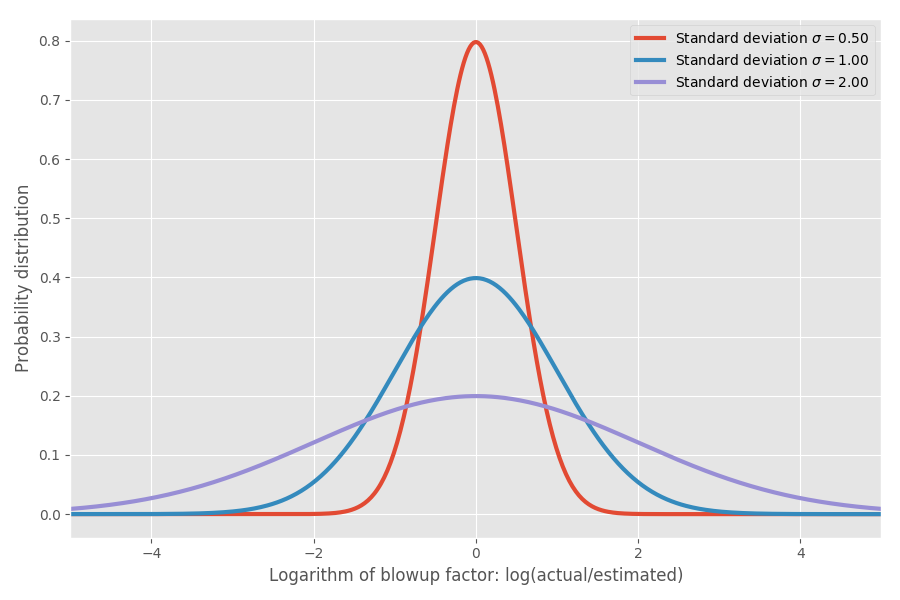
Просто чтобы показать реальные цифры: когда log(actual / estimated) = 1, то коэффициент инфляции exp(1) = e = 2.72. Одинаково вероятно то, что проект растянется в exp(2) = 7.4 раз, и то, что он завершится в exp (-2) = 0.14, т. е. в 14% от предполагаемого времени. Интуитивно причина, по которой среднее значение настолько велико, заключается в том, что задачи, которые выполняются быстрее, чем предполагалось, не могут компенсировать задачи, которые занимают гораздо больше времени, чем предполагалось. Мы ограничены 0, но не ограничены в другом направлении.
Это просто модель? Ещё бы! Но скоро я доберусь до реальных данных и на некоторых эмпирических данных покажу, что на самом деле она достаточно хорошо соответствует реальности.
Оценка сроков разработки программного обеспечения
Пока всё хорошо, но давайте действительно попробуем понять, что это значит с точки зрения оценки сроков разработки программного обеспечения. Предположим, мы смотрим на план из 20 различных программных проектов и пытаемся оценить: сколько времени потребуется, чтобы завершить их все.
Вот где среднее становится решающим. Средние складываются, а медианы нет. Поэтому, если мы хотим получить представление о том, сколько времени потребуется для завершения суммы N проектов, нужно смотреть на среднее значение. Допустим, у нас три разных проекта с одинаковыми σ = 1:
| Медиана | Среднее | 99% | |
|---|---|---|---|
| Задача A | 1.00 | 1.65 | 10.24 |
| Задача B | 1.00 | 1.65 | 10.24 |
| Задача C | 1.00 | 1.65 | 10.24 |
| SUM | 3.98 | 4.95 | 18.85 |
Обратите внимание, что средние складываются и 4,95 = 1,65*3, но другие столбцы этого не делают.
Теперь сложим три проекта с разными сигмами:
| Медиана | Среднее | 99% | |
|---|---|---|---|
| Задача A (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Задача B (σ = 1) | 1.00 | 1.65 | 10.24 |
| Задача C (σ = 2) | 1.00 | 7.39 | 104.87 |
| SUM | 4.00 | 10.18 | 107.99 |
Средние по-прежнему складываются, но реальность даже близко не соответствует наивной оценке в 3 недели, которую вы могли предположить. Обратите внимание, что сильно неопределённый проект с σ=2 доминирует над остальными по среднему времени завершения. А для 99-го процентиля он не просто доминирует, а буквально поглощает все остальные. Можем привести пример побольше.:
| Медиана | Среднее | 99% | |
|---|---|---|---|
| Задача A (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Задача B (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Задача C (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Задача D (σ = 1) | 1.00 | 1.65 | 10.24 |
| Задача E (σ = 1) | 1.00 | 1.65 | 10.24 |
| Задача F (σ = 1) | 1.00 | 1.65 | 10.24 |
| Задача G (σ = 2) | 1.00 | 7.39 | 104.87 |
| SUM | 9.74 | 15.71 | 112.65 |
Опять же, единственная неприятная задача в основном доминирует в расчётах оценки, по крайней мере, для 99% случаев. Даже по среднему времени один сумасшедший проект в конечном итоге занимает примерно половину времени, потраченного на все задачи, хотя по медиане у них близкие значения. Для простоты я предположил, что все задачи имеют одинаковую оценку по времени, но разные неопределённости. Математика сохраняется при изменении сроков.
Забавно, но у меня давно такое чувство. Сложение оценок редко работает, когда у вас много задач. Вместо этого выясните, какие задачи имеют самую высокую неопределённость: эти задачи обычно будут доминировать в среднем времени выполнения.
Диаграмма показывает среднее и 99-й процентиль как функцию неопределённости (σ):
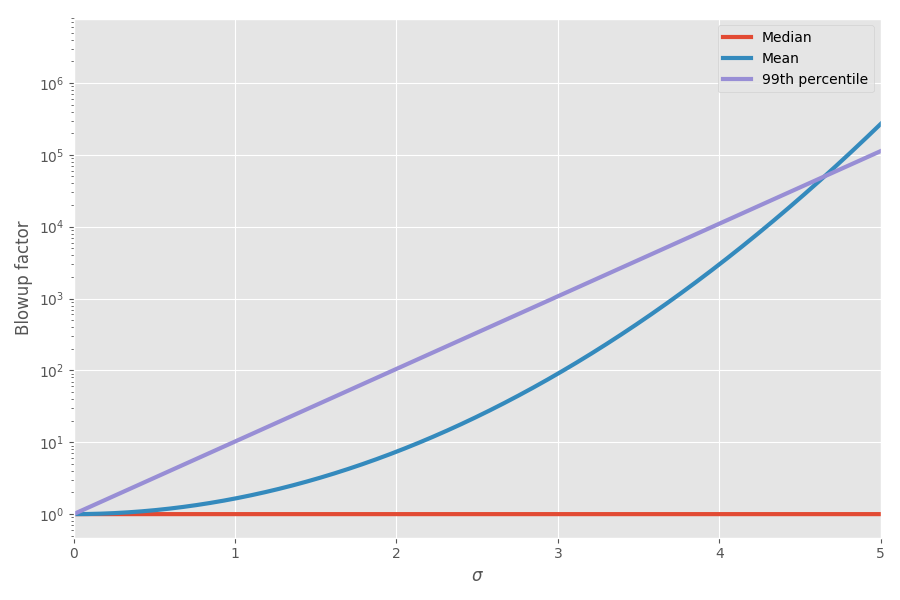
Теперь математика объяснила мои ощущения! Я начал учитывать это при планировании проектов. Я действительно думаю, что сложение оценок сроков выполнения задач сильно вводит в заблуждение и создаёт ложную картину, сколько времени займёт проект целиком, потому что у вас есть эти сумасшедшие перекошенные задачи, которые в конечном итоге отнимают всё время.
Где эмпирические данные?
Я долгое время хранил это в в разделе «любопытные игрушечные модели», иногда думая, что это аккуратная иллюстрация явления реального мира. Но однажды, бродя по сети, я наткнулся на интересный набор данных по оценке сроков проектов и фактическому времени их выполнения. Фантастика!
Давайте сделаем быстрый график разброса оценочного и фактического времени:
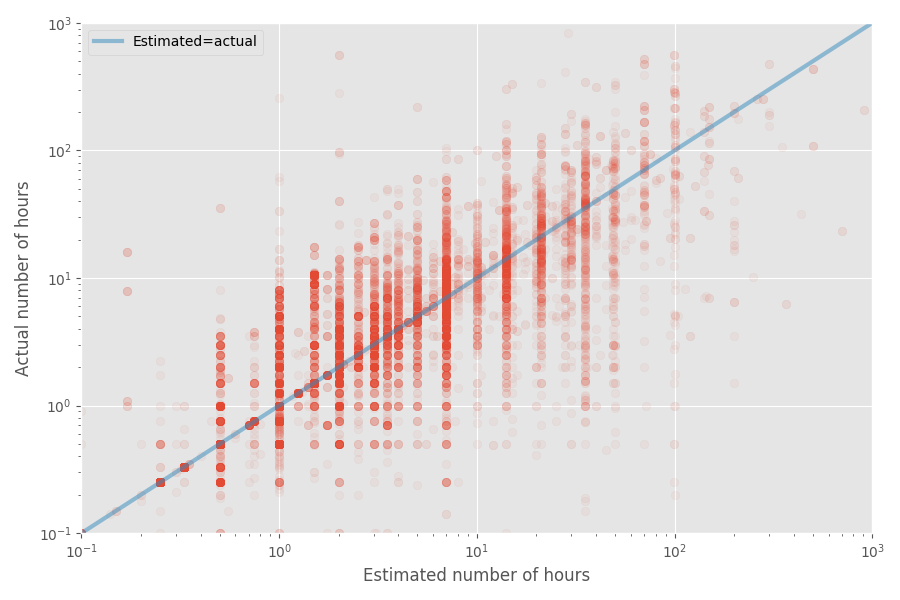
Медианный коэффициент инфляции для этого набора данных равен 1X, тогда как средний коэффициент равен 1,81x. Опять же, это подтверждает догадку, что разработчики хорошо оценивают медиану, но среднее значение оказывается намного выше.
Посмотрим на распределение коэффициента инфляции (логарифм):
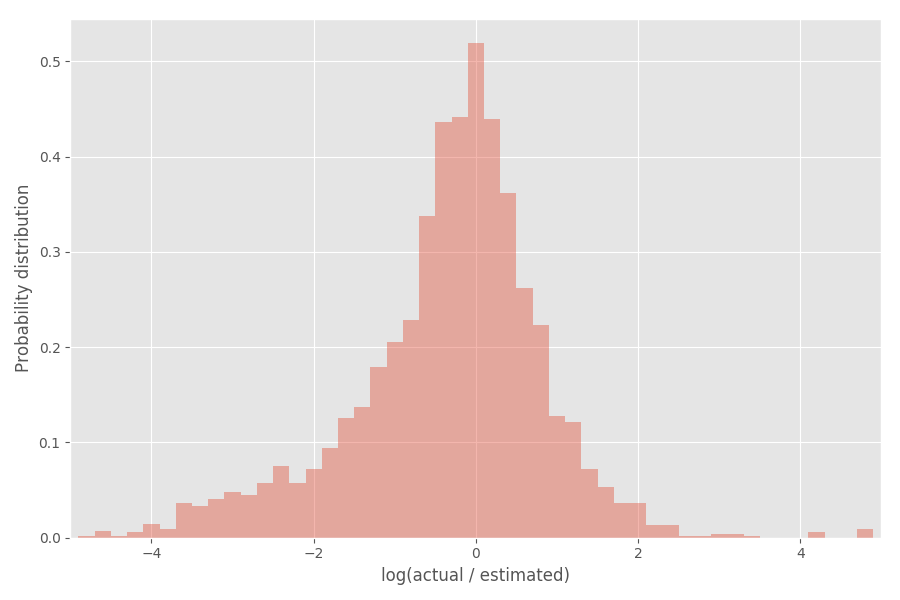
Как видите, он довольно хорошо центрирован вокруг 0, где коэффициент инфляции exp(0) = 1.
Возьмём статистические инструменты
Сейчас я собираюсь немного пофантазировать со статистикой — не стесняйтесь пропустить эту часть, если она вам не интересна. Что мы можем заключить из этого эмпирического распределения? Вы можете ожидать, что логарифмы коэффициента инфляции будут распределяться в соответствии с нормальным распределением, но это не совсем так. Обратите внимание, что σ сами случайны и варьируются для каждого проекта.
Один из удобных способов моделирования σ заключается в том, что они отбираются из обратного гамма-распределения. Если предположить (как и ранее), что логарифм коэффициентов инфляции распределён в соответствии с нормальным распределением, то «глобальное» распределение логарифмов коэффициентов инфляции завершается распределением Стьюдента.
Нанесём распределение Стьюдента на предыдущее:
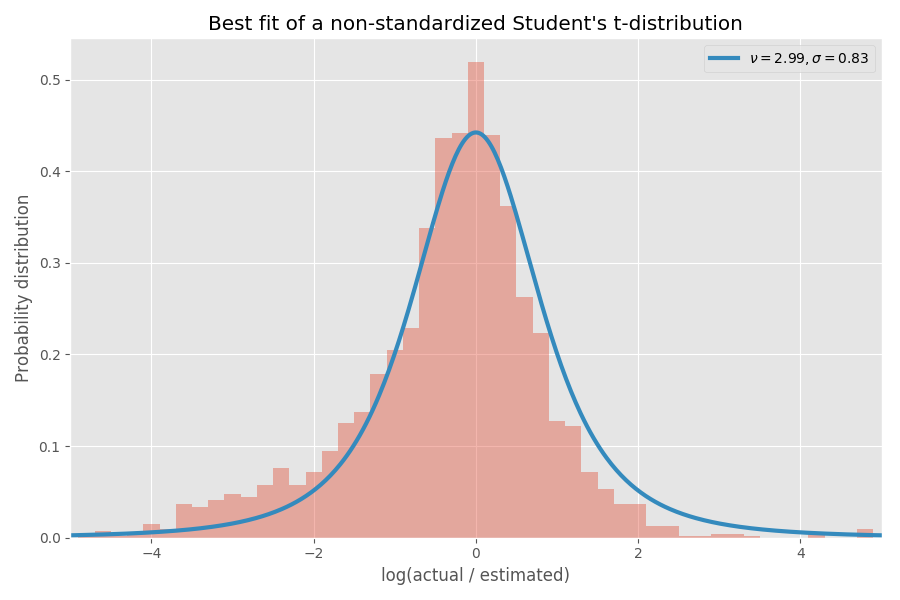
Прилично сходится, на мой взгляд! Параметры распределения Стьюдента также определяют обратное гамма-распределение значений σ:
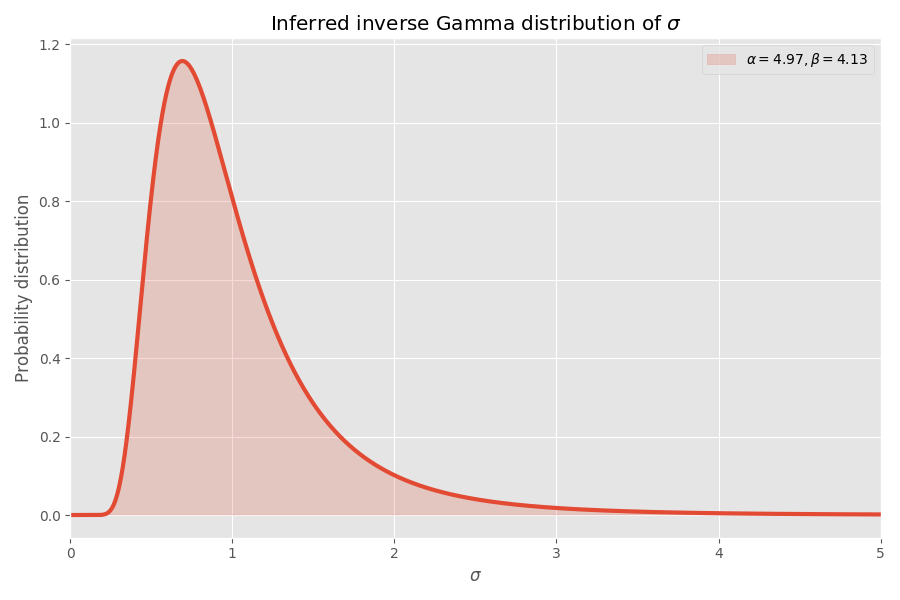
Обратите внимание, что значения σ > 4 очень маловероятны, но когда они происходят, то вызывают средний взрыв в несколько тысяч раз.
Почему программные задачи всегда занимают больше времени, чем вы думаете
Предполагая, что этот набор данных является репрезентативным для разработки программного обеспечения (сомнительно!), мы можем сделать ещё несколько выводов. У нас параметры для распределения Стьюдента, поэтому мы можем вычислить среднее время, необходимое для выполнения задачи, не зная σ для этой задачи.
В то время как медианный коэффициент инфляции из этой подгонки равен 1x (как и раньше), коэффициент инфляции 99% составляет 32x, но если вы перейдёте к 99,99-му процентилю, это колоссальные 55 миллионов! Одна (вольная) интерпретация заключается в том, что некоторые задачи в конечном итоге практически невозможны. Фактически, эти самые крайние случаи оказывают такое огромное влияние на среднее, что средний коэффициент инфляции любой задачи становится бесконечным. Это довольно плохие новости для тех, кто пытается уложиться в сроки!
Резюме
Если моя модель верна (большое если), то вот что мы можем узнать:
- Люди хорошо оценивают медианное время выполнения задачи, но не среднее.
- Среднее время оказывается значительно больше медианы из-за того, что распределение искажено (логнормальное распределение).
- Когда вы складываете оценки для n задач, всё становится ещё хуже.
- Задачи наибольшей неопределённости (скорее, наибольшего размера) часто могут доминировать по среднему времени, необходимому для выполнения всех задач.
- Среднее время выполнения задачи, о которой мы ничего не знаем, на самом деле бесконечно.
Примечания
- Очевидно, выводы основаны только на одном наборе данных, который я нашёл в интернете. Другие наборы данных могут дать другие результаты.
- Моя модель, конечно, тоже очень субъективна, как и любая статистическая модель.
- Я был бы рад применить модель к гораздо большему набору данных, чтобы увидеть, насколько она устойчива.
- Я предположил, что все задачи самостоятельны. На самом деле у них может быть корреляция, которая сделает анализ намного более раздражающим, но (я думаю) в конечном итоге с аналогичными выводами.
- Сумма логнормально распределённых значений не является другим логнормально распределённым значением. Это слабость данного распределения, так как вы можете утверждать, что большинство задач — это просто сумма подзадач. Неплохо, если бы наше распределение было устойчивым.
- Я удалил из гистограммы маленькие задачи (расчётное время меньше или равно 7 часам), так как они искажают анализ и там был странный всплеск ровно на 7.
- Код лежит на Github, как обычно.
Автор: m1rko






