В научной среде очень важную роль играет визуализация данных и оформление теории. Для удобного и красивого представления формул часто используются инструменты реализующие LaTeX-команды, например Markdown и MathJax.
Для Джулии также существует набор пакетов позволяющих использовать синтаксис LaTeX 'a, а в связке с средствами символьной алгебры мы получаем мощный инструмент для оперирования формулами.
Скачиваем и подключаем всё что нужно на сегодня
using Pkg
Pkg.add("Latexify")
Pkg.add("LaTeXStrings")
Pkg.add("SymEngine")
using Latexify, LaTeXStrings, Plots, SymEngineLaTeXStrings
LaTeXStrings небольшой пакет, облегчающий ввод уравнений LaTeX в строковых литералах на языке Julia. При использовании обычных строк в Julia для ввода строкового литерала со встроенными уравнениями LaTeX необходимо вручную избегать всех обратных слешей и знаков доллара: например, $ alpha^2 $ пишется $\alpha^2$. Кроме того, хотя IJulia способна отображать отформатированные уравнения LaTeX (через MathJax), с обычными строками такое не сработает. Посему, пакет LaTeXStrings определяет:
- Класс
LaTeXString(подтипString), который работает как строка (для индексации, преобразования и т. д.), Но автоматически отображается как текст / латекс в IJulia. - Строковые макросы
L"..."иL"""...""", которые позволяют вводить уравнения LaTeX без экранирования от обратной косой черты и знаков доллара (и которые добавляют для вас знаки доллара, если вы их опускаете).
S = L"1 + alpha^2"В REPL выйдет:
"$1 + \alpha^2$"а Jupyter отобразит:
Индексация работает как с обычными строками:
S[4:7]
"+ \a"Такие строки могут быть полезны при оформлении графиков
x = [-3:0.1:3...]
y1 = x .^2
α = 10
y2 = x .^4 / α;
plot(x,y1, lab = "$x^2_i$")
plot!(x,y2, lab = L"x^4_i/alpha")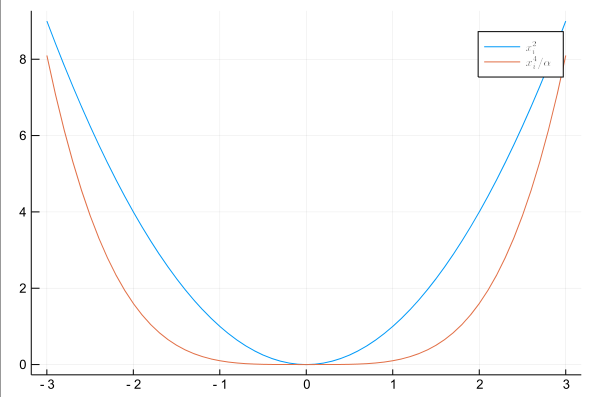
Latexify
Более функциональным пакетом является Latexify (Руководство). Он предназначен для генерации математики LaTeX из объектов julia. Этот пакет использует гомологичность Джулии для преобразования выражений в строки в формате LaTeX. Latexify.jl предоставляет функции для преобразования ряда различных объектов Julia, в том числе:
- Выражения,
- Строки,
- Numbers (включая рациональные и комплексные),
- Символические выражения из SymEngine.jl,
- ParameterizedFunctions и ReactionNetworks из DifferentialEquations.jl
а также массивы всех поддерживаемых типов.
ex = :(x/(y+x)^2) # выражение
latexify(ex)
str = "x/(2*k_1+x^2)" # строка
latexify(str)
Массив разнотипных элементов:
m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))]
latexify(m)![$ left[ begin{array}{ccc} frac{2}{3} & e^{ - c cdot t} & 1+3textit{i} \ frac{x}{x + k_{1}} & Gammaleft( n right) & log_{10}left( x right) \ end{array} right] $](https://www.pvsm.ru/images/2019/04/15/djuliya-v-latekse-6.svg "Джулия в латексе - 6")
Можно задать функцию выводящую формулы и копирующую их в буфер в виде понятном для Хабра:
function habr(formula)
l = latexify(formula)
res = "$$display$$l$display$$n"
clipboard(res)
return l
end
habr(ex)
<p>$<!-- math>$$display$$frac{x}{left( y + x right)^{2}}$$display$$</math -->$</p>Следует иметь ввиду
latexify("x/y") |> display
latexify("x/y") |> print$frac{x}{y}$
SymEngine
SymEngine — пакет предоставляющий символьные вычисления, которые можно визуализировать в вашем Jupyter с помощью Latexify.
Можно задавать символы строками и котировками (quote):
julia> a=symbols(:a); b=symbols(:b)
b
julia> a,b = symbols("a b")
(a, b)
julia> @vars a b
(a, b)Зададим матрицу и красиво отобразим ее
u = [symbols("u_$i$j") for i in 1:3, j in 1:3]
3×3 Array{Basic,2}:
u_11 u_12 u_13
u_21 u_22 u_23
u_31 u_32 u_33
u |> habr![$ left[ begin{array}{ccc} u_{11} & u_{12} & u_{13} \ u_{21} & u_{22} & u_{23} \ u_{31} & u_{32} & u_{33} \ end{array} right] $](https://www.pvsm.ru/images/2019/04/15/djuliya-v-latekse-9.svg "Джулия в латексе - 9")
Предположим у нас вектора
C = symbols("Ω_b/Ω_l")
J = [symbols("J_$i") for i in ['x','y','z'] ]
h = [0, 0, symbols("h_z")]
3-element Array{Basic,1}:
0
0
h_zкоторые надо векторно помножить
using LinearAlgebra
× = cross
latexify(J×h, transpose = true)$$display$$begin{equation} left[ begin{array}{c} J_{y} cdot h_{z} \ - J_{x} cdot h_{z} \ 0 \ end{array} right] end{equation} $$display$$
Полноценные матричные вычисления:
dJ = C*(u*J.^3)×h
latexify( dJ, transpose = true)
habr(ans)$$display$$begin{equation} left[ begin{array}{c} frac{h_{z} cdot left( u_{21} cdot J_{x}^{3} + u_{22} cdot J_{y}^{3} + u_{23} cdot J_{z}^{3} right) cdot Omega_{b}}{Omega_{l}} \ frac{ - h_{z} cdot left( u_{11} cdot J_{x}^{3} + u_{12} cdot J_{y}^{3} + u_{13} cdot J_{z}^{3} right) cdot Omega_{b}}{Omega_{l}} \ 0 \ end{array} right] end{equation} $$display$$
а вот такой нехитрой цепочкой можно найти детерминант и отправить его на Хабр
u |> det |> habr
Рекурсивненько! Обратная матрица наверно посчитается сходным образом:
u^-1 |> habr$$display$$ left[ begin{array}{ccc} frac{1 - frac{u_{12} cdot left( frac{ - u_{21}}{u_{11}} - frac{left( frac{ - u_{31}}{u_{11}} + frac{u_{21} cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{11} cdot left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right)} right) cdot left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right)}{u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} - frac{u_{13} cdot left( frac{ - u_{31}}{u_{11}} + frac{u_{21} cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{11} cdot left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right)} right)}{u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}}}}{u_{11}} & frac{frac{ - u_{12} cdot left( 1 + frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right) cdot left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} + frac{u_{13} cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right) cdot left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)}}{u_{11}} & frac{frac{ - u_{13}}{u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}}} + frac{u_{12} cdot left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right)}{left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right) cdot left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)}}{u_{11}} \ frac{frac{ - u_{21}}{u_{11}} - frac{left( frac{ - u_{31}}{u_{11}} + frac{u_{21} cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{11} cdot left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right)} right) cdot left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right)}{u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}}}}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} & frac{1 + frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right) cdot left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)}}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} & frac{ - left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right)}{left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right) cdot left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)} \ frac{frac{ - u_{31}}{u_{11}} + frac{u_{21} cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{11} cdot left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right)}}{u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}}} & frac{ - left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{left( u_{22} - frac{u_{12} cdot u_{21}}{u_{11}} right) cdot left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)} & left( u_{33} - frac{u_{13} cdot u_{31}}{u_{11}} - frac{left( u_{23} - frac{u_{13} cdot u_{21}}{u_{11}} right) cdot left( u_{32} - frac{u_{12} cdot u_{31}}{u_{11}} right)}{u_{22} - frac{u_{12} cdot u_{21}}{u_{11}}} right)^{-1} \ end{array} right] $$display$$
Если хотите сделать больно Матжаксу своего браузера, поставьте минус вторую степень (квадрат обратной матрицы)
Кстати, SymEngine считает производные:
dJ[1] |> habr
diff(dJ[1], J[1]) |> habr
К слову, Джулия может использовать из LaTeX 'a не только формулы, но и графики. И если вы установили MikTex и уже скачали pgfplots, то с помощью соответствующего окружения его можно сдружить с Джулией, что предоставит возможность строить гистограммы, трехмерные графики, ошибки и рельефы с изолиниями, а потом это интегрировать в LaTeX документ.
На этом с формулами всё, но не с символьными вычислениями: у Джулии еще есть более сложные и интересные решения для символьной алгебры, с которыми мы обязательно разберемся как-нибудь в следующий раз.
Автор: Yermack
