Эта статья может быть интересна тем, кто занимается сжатием данных или хочет написать собственный архиватор.
Статья написана, в основном, по материалам блога, который ведёт Fabian Giesen.
Введение
Метод энтропийного кодирования rANS (range + ANS) — родной брат алгоритма FSE, о котором я уже писал ранее. Аббревиатура ANS означает Asymmetric Numeral Systems, а слово range в названии намекает на схожесть этого метода с интервальным кодированием. Автор rANS — Ярек Ду́да.
Метод rANS позволяет достичь практически оптимального сжатия при очень высокой скорости работы. В этом rANS ничем не уступает FSE, что неудивительно: оба алгоритма построены на общей теоретической базе. Однако алгоритм rANS значительно проще в реализации, чем FSE.
Сначала будет длинная «теоретическая» часть, а потом мы попробуем написать простейший архиватор.
Описание метода
Работа алгоритма определяется следующими несложными формулами:
Кодирование: C(s,x): x := (x / Fs) * M + Bs + (x % Fs)
Декодирование: D(x): s = sym[x % M], x := Fs * (x / M) + (x % M) - Bs
Давайте разберем их подробно.
Функция кодирования C(s, x) принимает на вход символ s, который нужно закодировать (пусть это целое число), и текущее состояние кодера x (тоже целое число).
Fs — частота символа s. Деление на Fs выше — целочисленное.
M — сумма частот всех символов алфавита (M = Σ Fs).
Вs — начало интервала, соответствующего кодируемому символу (на рисунке ниже).
x % Fs — остаток от деления x на Fs.
Принцип работы такой же, как в арифметическом кодировании: берем отрезок [0, M) и делим на части так, чтобы каждому символу s соответствовал интервал, по размеру равный частоте символа Fs. Попадание значения x % M в какой-либо интервал обозначает кодирование соответствующего символа.
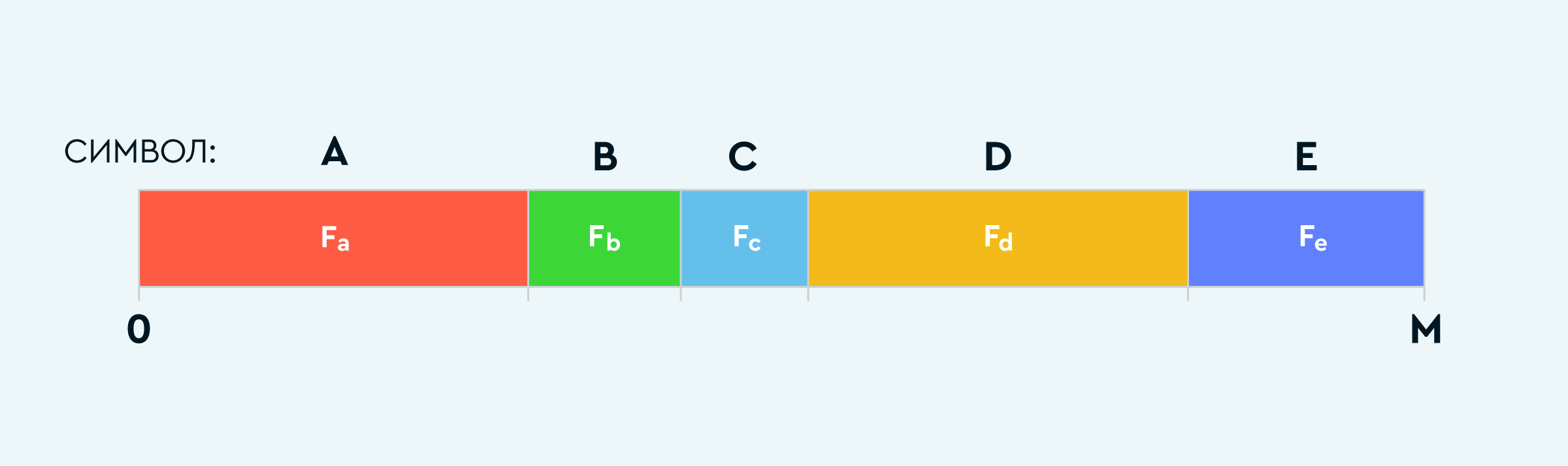
В начале кодирования инициализируем x произвольным подходящим значением, а затем вычислим функцию C(s, x) для всех кодируемых символов последовательно.
Каждое вычисление функции C(s, x) увеличивает значение x. Когда оно становится слишком большим, следует сбросить данные в output:
while (x >= x_max) {
writeToStream(x % b); // записываем данные
x /= b; // уменьшаем x
}Этот шаг называется ренормализация. После него можно продолжить кодирование.
Выше в коде появились новые константы: x_max и b. В теории, числа M, b и x_max связаны некоторыми соотношениями, но на практике эффективнее всего использовать следующие значения, если для состояния x используется тип uint32:
M = 2^k, где k <= 16
b = 2^16 (половина от размера uint32)
Выбор M = 2^k обусловлен тем, что в функции декодирования присутствует деление на M, таким образом деление с остатком можно будет заменить на битовые операции.
Значение k выбирается из следующих соображений: чем оно больше, тем выше точность Fs и тем эффективнее сжатие. При этом надо учитывать некоторые накладные расходы на хранение таблицы частот, поэтому не всегда стоит использовать максимальные значения k.
Значение x_max должно быть такое, чтобы не возникало переполнения. Исходя из функции кодирования получаем, что x < uint32_max * Fs / M или немного по-другому: x_max <= (b * L) * Fs / M, где L <= uint32_max / b. В реальном коде условие принимает вид x / b >= L / M * Fs, чтобы избежать переполнения при вычислениях.
Значение b = 2^16 (половина размера uint32) выбрано таким образом, что если x превышает x_max, то достаточно одного деления на b для продолжения работы. В результате, цикл while завершится после первой же итерации, а значит его можно заменить на простой if.
В итоге функция кодирования приобретает следующий вид:
typedef uint32_t RansState;
constexpr uint32_t RANS_L = 1u << 16;
constexpr uint32_t k = 10; // для примера
constexpr uint32_t RANS_M = 1u << k; // M = 2^k
// Кодируем символ s
void RansEnc(RansState& x, uint32_t s, RansOutBuf& out)
{
assert(x >= RANS_L); // Этот инвариант должен выполняться всегда
uint32 Fs = freq[s]; // Частота символа s
uint32 Bs = range_start[s]; // Начало интервала s
assert(Fs > 0 && Fs <= RANS_M);
// renormalize
if ((x >> 16) >= (RANS_L >> k) * Fs) { // x / b >= L / M * Fs
out.put( x & 0xffff );
x >>= 16;
}
x = ((x / Fs) << k) + Bs + (x % Fs); // C(s,x)
assert(x >= RANS_L); // Этот инвариант должен выполняться всегда
}В конце кодирования надо сохранить значение x, так как с него начнётся декодирование. И да, декодировать мы будем от конца к началу, то есть от последнего закодированного символа к первому. (В статье про FSE этот момент объясняется достаточно подробно.)
Хочу ещё немного остановиться на том, как работает формула кодирования.
x := (x / Fs) * M + Bs + (x % Fs)
После вычисления (x / Fs) * M в переменной x появляется k свободных младших бит (вспомним, что M = 2 ^ k). Добавление + Bs + (x % Fs) по сути записывает в эти биты определенное значение из интервала символа s, ведь Bs — это начало интервала, а (x % Fs) — число в пределах этого интервала (размер интервала равен Fs). Таким образом, при декодировании мы можем определить закодированный символ по тому интервалу, в который попадает (x % M).
Декодирование
Перейдем к функции декодирования.
D(x): s = sym[x % M], x := Fs * (x / M) + (x % M) - BsКак мы уже поняли выше, искомый символ s определяется остатком от деления x % M. В какой интервал попало значение (x % M), такой символ и был закодирован.
Ранее мы специально определили M = 2 ^ k, чтобы упростить функцию декодирования. В итоге получилось так:
uint32_t RansDecode(RansState& x, RansInBuf& in)
{
assert(x >= RANS_L); // Проверяем инвариант
uint32_t x_mod = x & (RANS_M - 1); // = x % M
// определяем интервал, в который попал x_mod, табличным методом
assert(x_mod < dct.size());
uint32_t s = dct[x_mod]; // декодированный символ
uint32 Fs = freq[s]; // Частота символа s
uint32 Bs = range_start[s]; // Начало интервала для s
x = (x >> k) * Fs + x_mod - Bs;
// renormalize
if (x < RANS_L) {
x = (x << 16) | in.read16(); // Считываем 16 бит
}
assert(x >= RANS_L); // Проверяем инвариант
return s;
}Декодирование начинается с того же x, который получился в конце кодирования. Для этого его надо сохранить вместе с закодированными данными.
В конце декодирования состояние декодера x должно получиться точно такое же, с которого начиналось кодирование. Вообще, на каждом шаге x должен быть точно такой же, как на соответствующем этапе кодирования. Этот факт очень помогает при отладке.
Как можно заметить, декодирование работает быстрее кодирования, так как нет операций деления.
Наиболее сложным моментом в функции декодирования является способ определения, в какой интервал попало значение (x % M).
Самый простой и быстрый метод — использовать таблицу sym[], размером M. В этом случае мы получим таблицу такого же размера, как в алгоритме FSE, с тем отличием, что в rANS таблица не «перемешана», символы идут по порядку, и такую таблицу намного легче построить.
Главным недостатком этого подхода является размер таблицы sym, который растёт экспоненциально с увеличением k.
Alias method
Для более эффективного определения попадания в интервал был изобретён alias method. Этот метод позволяет быстро определять искомый интервал, используя небольшие таблицы — по количеству символов в алфавите.
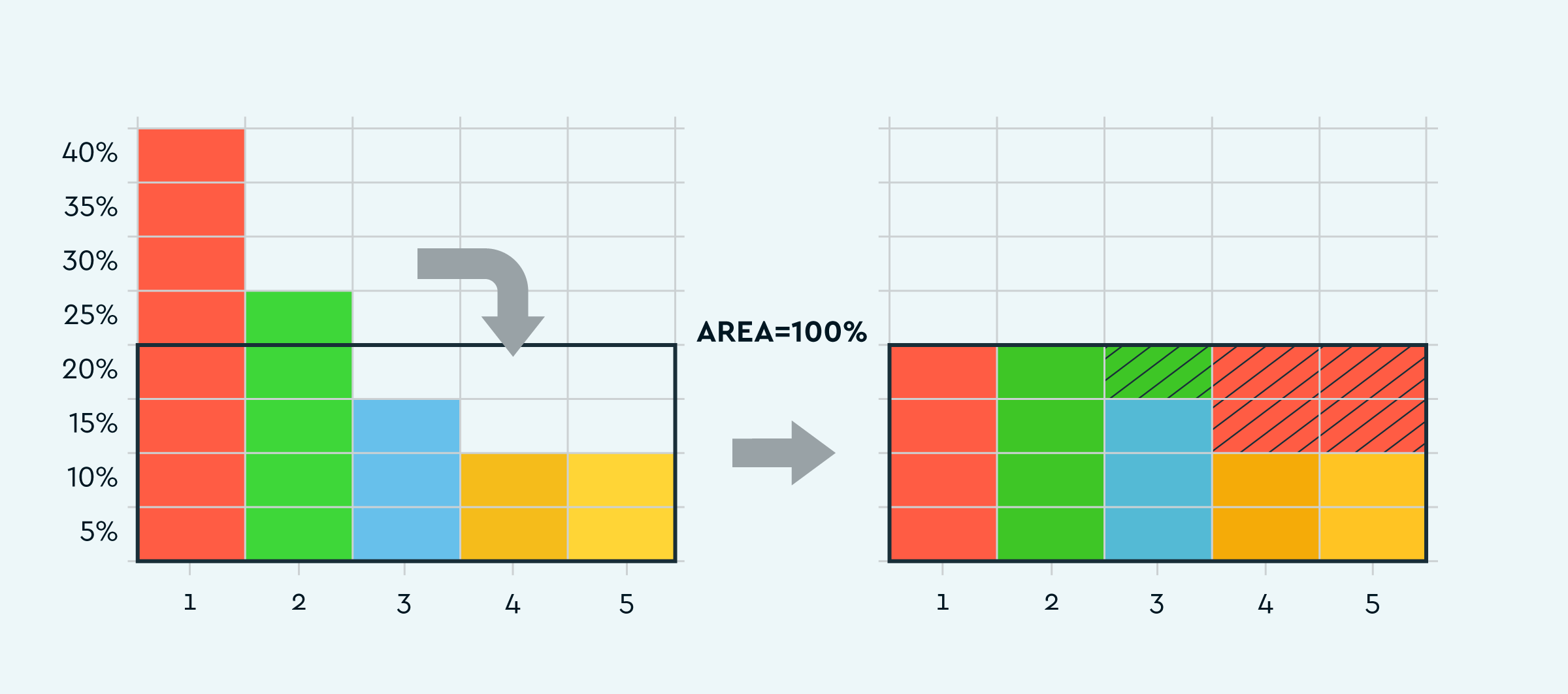
Длинное и пространное объяснение можно почитать тут: Darts, Dice and Coins. Опишу суть метода вкратце: берем кусок самого длинного интервала и присоединяем его к самому короткому интервалу так, чтобы суммарный размер получился ровно M / N (где N — количество символов в алфавите). Оказывается, если последовательно так делать, то в итоге всегда получится N пар размером M / N.
Естественно, M должно делиться на N. А если вспомнить, что у нас M = 2^k, то и размер алфавита получается тоже должен быть степенью двойки. Это не проблема, так как всегда можно дополнить алфавит до нужного размера неиспользуемыми символами с нулевой частотой.
То, что интервал символа оказывается разделён на несколько частей, немного усложняет процедуру кодирования, но не сильно. Если вспомнить FSE, так там интервалы вообще были размазаны по всему диапазону, как будто над ними поработал бешеный миксер, и ничего, работало =)
Определить искомый интервал несложно: делим x на N, и попадаем в одну из пар. Дальше сравниваем остаток от деления x % N с границей между отрезками в паре и попадаем либо в один интервал, либо в другой.
Пробуем на практике
Воспользуемся кодом готового примера.
Берём данные для сжатия из файла:
size_t in_size;
uint8_t* in_bytes = read_file("book1", &in_size);1. Сначала надо определиться со структурой данных.
Используем простейший вариант: будем кодировать по одному байту, используя алфавит [0… 255].
2. Следующим шагом нужно определить частоты символов алфавита:
(функция stats.count_freqs)
for (size_t i = 0; i < in_size; i++) {
freqs[in_bytes[i]]++;
}3. Итак, у нас есть частоты символов, но теперь их нужно нормализовать, то есть пропорционально уменьшить (или увеличить) так, чтобы в сумме получилось M = 2 ^ k. Это не такая простая задача, как может показаться, поэтому используем готовую функцию:
stats.normalize_freqs(...);Кстати, нужно определиться с величиной k. Так как наш алфавит состоит из 256 символов, то k меньше 8 брать не стоит. Для начала возьмём по максимуму — 16, позже попробуем и другие значения.
4. Строим alias table:
stats.make_alias_table();5. Кодируем с конца, чтобы потом декодировать в нормальном порядке.
RansState rans; // Состояние rANS, которое ранее обозначалось x
RansEncInit(&rans); // инициализируем начальным значением
uint8_t* ptr = out_buf + out_max_size; // *end* of output buffer
for (size_t i = in_size; i > 0; i--) { // NB: working in reverse!
int s = in_bytes[i - 1];
RansEncPutAlias(&rans, &ptr, &stats, s, prob_bits);
}
// Записываем конечное состояние. С него потом начнётся декодирование.
RansEncFlush(&rans, &ptr);Далее пример по ссылке декодирует сжатые данные, используя готовый stats. В реальной жизни для декодирования нужно сохранять таблицу частот (stats) вместе со сжатыми данными. В самом простом случае на неё придётся потратить N * k бит.
Как и обещал выше, давайте посмотрим на результаты сжатия при различных значениях k (в коде это prob_bits) с учётом прибавки размера из-за записи таблицы частот:
(Исходный размер файла book1: 768771)
k = 16: 435059 + 512 = 435571 bytes
k = 15: 435078 + 480 = 435558 bytes
k = 14: 435113 + 448 = 435561 bytes
k = 13: 435239 + 416 = 435655 bytes
k = 12: 435603 + 384 = 435987 bytes
k = 11: 436530 + 352 = 436882 bytes
k = 10: 440895 + 320 = 441215 bytes
k = 9: 453418 + 288 = 453706 bytes
k = 8: 473126 + 256 = 473382 bytes
Можно видеть, что чем выше k, тем лучше сжатие. Но в определённый момент (при k=16) накладные расходы на таблицу частот начинают перевешивать выгоду от увеличения точности. Если сжимать файл меньшего размера, этот эффект проявится на меньших k.
Также нужно сказать пару слов о трюке под названием «interleaved rANS», который дополнительно реализован в рассматриваемом примере. Идея заключается в том, что поочередное использование двух независимых переменных состояния эффективнее использует параллелизм процессора. В результате декодирование работает ещё быстрее.
В заключение хочу заметить, что выбранный способ сжатия файла слишком простой. Он никак не учитывает особенности данных, из-за чего сжатие получается далеко не оптимальным. Если присмотреться ко входным данным, то можно обнаружить, что некоторые буквосочетания встречаются чаще других, а некоторые вообще не встречаются. Используя этот факт, можно значительно улучшить сжатие. Но это тема для отдельной статьи.
Послесловие
Зачем писать собственный архиватор, когда существует множество проверенных временем утилит? Ответ достаточно прост: архиваторы, заточенные под конкретный формат, сжимают намного лучше.
Мы в компании Playrix при разработке игр часто упираемся в необходимость уменьшать размер билда. Игры постоянно развиваются, количество контента растет, а место ограничено.
В очередной раз с тоской глядя на ресурсы, мы поняли, что некоторые файлы можно сжать намного лучше, чем это делает zip, если учесть их структуру. В ходе экспериментов у нас получилось значительно уменьшить размер собственного формата анимаций, также есть некоторые подвижки в сжатии файлов графики.
При разработке алгоритмов сжатия универсальный энтропийный кодер, такой как rANS или FSE, показывает себя незаменимым инструментом. Он полностью берёт на себя задачу записи символов наименьшим количеством бит, позволяя разработчику сосредоточиться на основных деталях алгоритма. А ещё он очень быстро работает и при кодировании, и при декодировании.
Надеюсь, данная статья поможет вам познакомиться с rANS и начать использовать его в ваших проектах.
Ссылки
Здесь можно посмотреть работающие примеры реализации rANS (с разными вариантами оптимизаций):
Fabian Giesen: github.com/rygorous/ryg_rans
В блоге Fabian’а можно почитать интересные детали и подробности (на английском):
→ rANS notes
→ rANS with static probability distributions
→ rANS in practice
Автор: Biga







