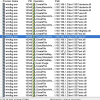
Предыстория: моя жена постоянно норовить как-нибудь мне напортачить: поставить будильник на 3 часа ночи, поменять мелодию звонка, снести настройки синхронизации, удалить свою смс и потом доказывать, что она этого не говорила.
Шутки шутками, но в какой-то момент я решил: “Довольно!” — и поставил графический пароль на свой Андройд.
Жена усмехнулась и сказала, что подберёт. Я посмеялся в ответ, на том и разошлись. Только теперь её волновал вопрос, как подобрать, а меня какова вероятность этого события.
Самая первая и логичная мысль придумать математический способ вычисления комбинаций.
Нужно задать начальные условия:
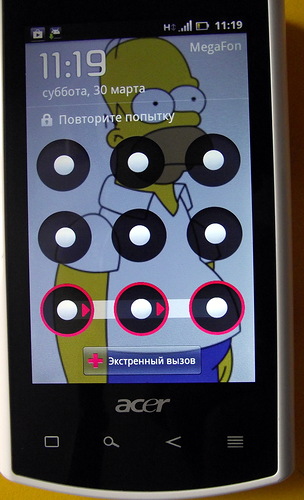
- Направление имеет значение
- Для соединения двух точек они должны быть в прямой видимости. То есть первая может быть соединена пальцем со второй, но не с третьей.
- Количество точек: от 5 до 9. Назовём один росчерк, одно соединение — хопом. То есть у нас может быть от 4 до 8 хопов.
Попытки влоб просчитать варианты математически не увенчались успехом. Накладываемые условия не позволили выявить правила.
Следующий шаг: перебор. Не то чтобы я надеялся перебрать все десятки тысяч вариантов. Основная мысль была — найти закономерности.
Я потратил на рисование схем несколько часов. Но все закономерности упирались в симметрию и то, что все угловые точки равнозначны, как и все промежуточные (кроме центральной).

Но когда нас пугали трудности?
Начал я всё-таки с одного хопа.

1 хоп — проще пареной репы — 56 вариантов,
2 хопа — ничего сложного — 304 варианта
3 хопа — пришлось потрудиться — 1400 вариантов
4 хопа — это было, кхм, утомительно — 5328 вариантов
5 хопов — мама миа и вырванные волосы — результат неизвестен.
Дальше я уже решил не насиловать свой и вспомнить давно забытое программирование.
Расчехлил турбопаскаль, стряхнул пыль с переменных и начал разрабатывать алгоритм.
После 4 лет паузы и простеньких скриптов на баше мне потребовался целый вечер на отладку программы. Даром, что алгоритм родился минут за 20.
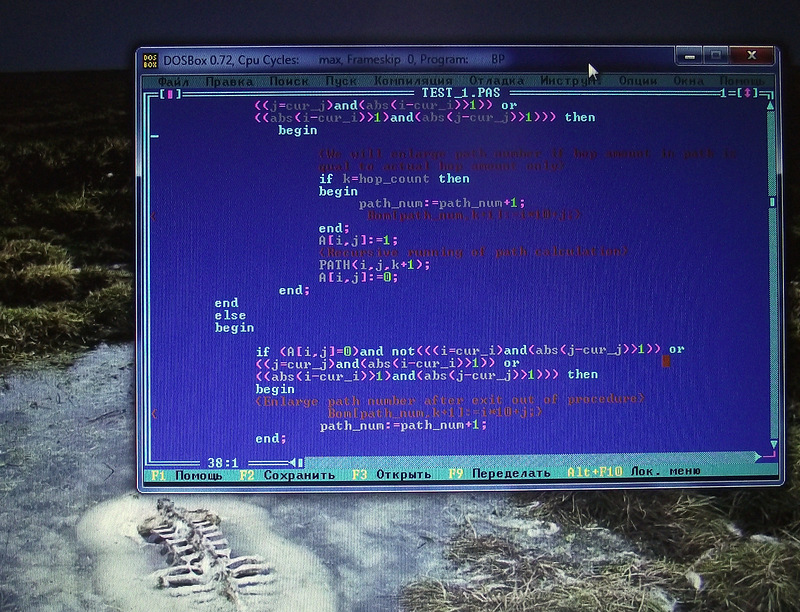
Program First;
Uses Crt;
VAR
i,j,k,cur_i,cur_j,hop_count:byte;
A:array[1..3,1..3] of byte;
Bom:Array[1..10000,1..5] of byte;
path_num,total,m,n:longint;
Procedure PATH(cur_i,cur_j:byte; k:byte);
VAR
i,j:byte;
m,n:integer;
begin
{We will calclate only path amount, but not detailed paths, because of
limitation to array size.
Actually you can make detailed path up to 5 hops. You just should uncomment
calculating of array 'Bom'}
A[cur_i,cur_j]:=1;
for i:=1 to 3 do
begin
for j:=1 to 3 do
begin
{ Bom[path_num,k]:=cur_i*10+cur_j; }
if k<hop_count then
begin
{Checking possibility of doing next-hop}
if (A[i,j]=0)and not(((i=cur_i)and(abs(j-cur_j)>1)) or
((j=cur_j)and(abs(i-cur_i)>1)) or
((abs(i-cur_i)>1)and(abs(j-cur_j)>1))) then
begin
{We will enlarge path number if hop amount in path is
qual to actual hop amount only}
if k=hop_count then
begin
path_num:=path_num+1;
{ Bom[path_num,k+1]:=i*10+j;}
end;
A[i,j]:=1;
{Recursive running of path calculation}
PATH(i,j,k+1);
A[i,j]:=0;
end;
end
else
begin
if (A[i,j]=0)and not(((i=cur_i)and(abs(j-cur_j)>1)) or
((j=cur_j)and(abs(i-cur_i)>1)) or
((abs(i-cur_i)>1)and(abs(j-cur_j)>1))) then
begin
{Enlarge path number after exit out of procedure}
{ Bom[path_num,k+1]:=i*10+j;}
path_num:=path_num+1;
end;
end;
end;
end;
end;
begin
{A[x,y] - Array of 0 and 1.
0 - this point isn't in path yet. You can move here.
1 - this point is in path already. You can't move here.
}
ClrScr;
writeln ('Hello, Habrahabr. Let','''','s count amount of Android Graphical passwords.');
writeln;
i:=1;
j:=1;
k:=1;
for hop_count:=4 to 8 do
begin
path_num:=1;
for i:=1 to 3 do
for j:=1 to 3 do
begin
{ Bom[path_num,k]:=10*i+j;}
PATH(i,j,k);
a[i,j]:=0;
end;
writeln('Hops: ',hop_count,'. Path amount: ',path_num-1);
total:=total+path_num-1;
end;
writeln('===========================');
writeln('Total amount: ',total);
{Output of full list of paths.}
{for m:=1 to path_num do
begin
write('Path ', m,': (');
for n:=1 to hop_count do
begin
write(Bom[m,n],' ');
end;
writeln(')');
readln;
end;{}
readln;
end.
Вот вывод количества вариантов для каждого количество хопов. Как видно, с 1 по 4 цифра совпадает с практическими рассчётами, а при количестве хопов больше 8 — путей нет, что логично.
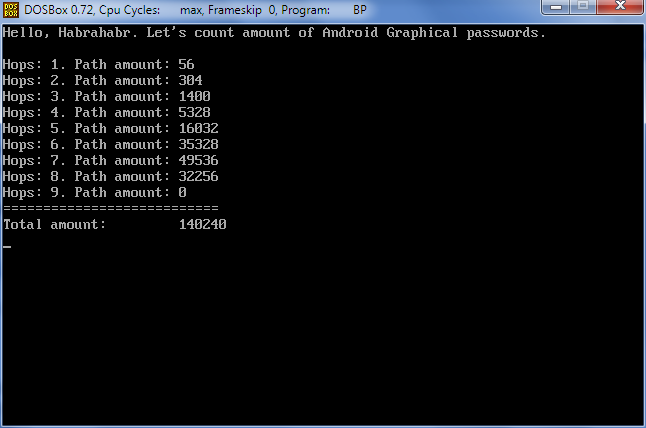
Паскаль имеет ограничение в 64 кБ на размер массива. Поэтому массив даже из Byte в несколько десятков тысяч элементов невозможен. Заморачиваться с динамическим выделением памяти или записями не хотелось, поэтому просчитать сами пути в подробностях можно только до 4 хопов:
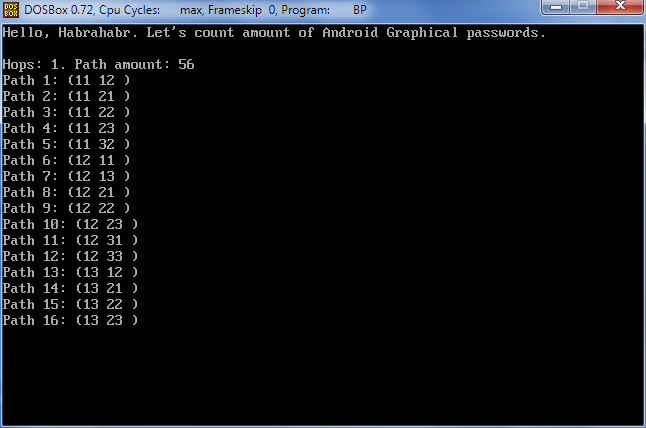
И вот долгожданный результат:
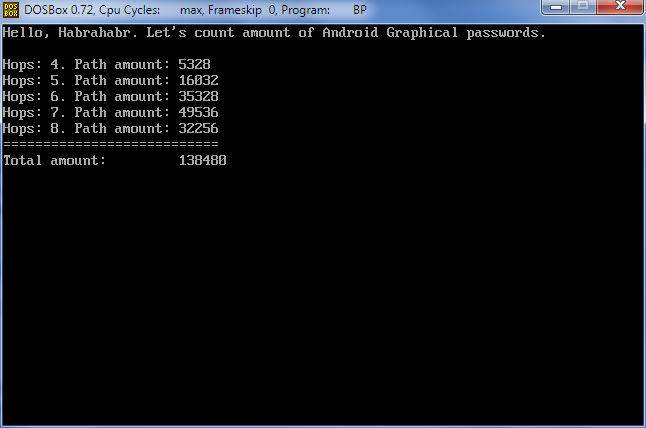
Итак, 138480 возможных вариантов.
Даже если из них исключить 50% извращённых вариантов, которые не каждый человек, лишённый шизофрении, сможет с первого раза набрать (впрочем, зачем шизофренику андроид), остаётся 69240 вариантов

Андроид даёт 20 попыток, после которых блокирует телефон.
Итак, 20/69240=0,0003. То есть, вероятность 0,03%.
“Ну-ну” — сказал я жене, показывая расчёты. “Ну-ну” — сказала мне жена, показывая разблокированный телефон.

Автор: eucariot