Коллапс волновой функции: алгоритм, вдохновлённый квантовой механикой

Алгоритм Wave Function Collapse генерирует битовые изображения, локально подобные входному битовому изображению.

Локальное подобие означает, что

• (C1) Каждый паттерн NxN пикселей в выходных данных должен хотя бы раз встречаться во входных данных.
• (Слабое условие C2) Распределение паттернов NxN во входных данных должно быть подобным распределению паттернов NxN в значительно большом количестве наборов выходных данных. Другими словами, вероятность встречи определённого паттерна в выходных данных должна быть близка к плотности таких паттернов во входных данных.

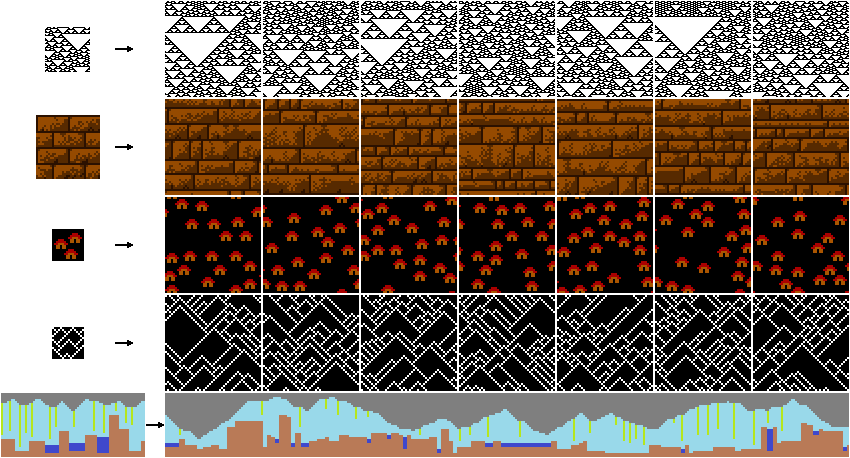
В примерах стандартным значением N является 3.

Алгоритм WaveFunctionCollapse (WFC) инициализирует выходное битовое изображение как полностью ненаблюдаемое состояние, в котором значение каждого пикселя является суперпозицией цветов входного битового изображения (поэтому если входное изображение чёрно-белое, то ненаблюдаемые состояния отображаются как различные оттенки серого). Коэффициентами этих суперпозиций являются вещественные, а не мнимые числа, поэтому в алгоритме не используется настоящая квантовая механика, скорее он был ею вдохновлён. Затем программа переходит в цикл наблюдения-распространения:

• На каждом этапе наблюдения среди ненаблюдаемого пространства выбирается область NxN, имеющая наименьшую энтропию Шеннона. Состояние этой области затем коллапсирует к состоянию определённости в соответствии с коэффициентами и распределением паттернов NxN во входящих данных.
• На каждом этапе распространения новая информация, полученная при коллапсе предыдущего этапа, распространяется по выходным данным.

На каждом этапе общая энтропия уменьшается, и в конце концов мы получаем полностью наблюдаемое состояние, коллапс волновой функции завершается.

Может случиться так, что в процессе распространения все коэффициенты для определённого пикселя становятся равными нулю. Это означает, что алгоритм пришёл к противоречию и не может выполняться дальше. Задача определения того, обеспечивает ли заданное битовое изображение другие нетривиальные битовые изображения, удовлетворяющие условию (C1), является NP-трудной, поэтому невозможно создать быстрое решение, всегда завершающее алгоритм. Однако на практике алгоритм сталкивается с противоречиями на удивление редко.

Алгоритм коллапса волновой функции реализован на C++, Python, Kotlin, Rust, Julia, Haxe, JavaScript и адаптирован под Unity. Официальные исполняемые файлы можно скачать с itch.io или запустить в браузере. WFC генерирует уровни в Bad North, Caves of Qud, нескольких более мелких играх, а также во множестве прототипов. Его создание привело к новому исследованию. Другие связанные работы, объяснения, интерактивные демо, руководства, туториалы и примеры см. в разделе про порты, форки и спин-оффы.

Посмотрите демонстрацию алгоритма WFC на YouTube: https://youtu.be/DOQTr2Xmlz0

Алгоритм

1. Считать входящее битовое изображение и подсчитать количество паттернов NxN.
   1. (необязательно) Дополнить данные паттернов повёрнутыми и отражёнными паттернами.
2. Создать массив с размерами выходных данных (в исходниках называемый «wave»). Каждый элемент этого массива обозначает состояние области размером NxN в выходных данных. Состояние области NxN является суперпозицией паттернов NxN входящих данных с булевыми коэффициентами (то есть состояние пикселя в выходных данных является суперпозицией входящих цветов с вещественными коэффициентами). Коэффициент False означает, что соответствующий паттерн запрещён, коэффициент true означает, что соответствующий паттерн пока не запрещён.
3. Инициализировать волну в полностью ненаблюдаемом состоянии, то есть где все булевы коэффициенты имеют значение true.
4. Повторять следующие шаги:
   1. Наблюдение:
      1. Найти элемент волны с минимальной ненулевой энтропией. Если таких элементов нет (если у всех элементов энтропия нулевая или неопределённая), то завершить цикл (4) и перейти к шагу (5).
      2. Коллапсировать этот элемент в состояние определённости в соответствии с его коэффициентами и распределением паттернов NxN входящих данных.
   2. Распространение: распространить информацию, полученную на предыдущем шаге наблюдения.
5. К данному моменту все элементы волны или имеют полностью наблюдаемое состояние (все коэффициенты, кроме одного, равны нулю) или находятся в состоянии противоречия (все коэффициенты равны нулю). В первом случае вернуть выходные данные. Во втором случае завершить работу, ничего не возвращая.

Генерация тайловых карт

Простейший нетривиальный случай алгоритма — это паттерн NxN=1x2 (точнее NxM). Если мы ещё больше упростим его, сохраняя не вероятности пар цветов, а вероятности самих цветов, то получим то, что называется «простой тайловой моделью». Фаза распространения в этой модели — это просто распространение зависимости соседства. Удобно инициализировать простую тайловую модель списком тайлов и данными об их соседстве (данные о соседстве можно рассматривать как большое множество очень маленьких сэмплов), а не сэмплируемым битовым изображением.

GIF | GIFV

Списки всех возможных пар соседних тайлов в практических тайлсетах могут быть достаточно длинными, поэтому чтобы укоротить перечисление, я реализовал для тайлов систему симметрии. В этой системе каждому тайлу должен назначаться его тип симметрии.

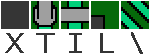
Заметьте, что тайлы имеют ту же симметрию, что и назначенные им буквы (другими словами, действия диэдральной группы D4 изометричны для тайлов и соответствующих букв). Благодаря этой системе достаточно перечислить пары соседних тайлов только до их симметрии, в несколько раз укорачивает список соседей для тайлсетов со множеством симметричных тайлов (даже в тайлсете рельефа Summer, несмотря на то, что рисунки не являются симметричными, система считает такие тайлы симметричными).

Заметьте, что неограниченный тайлсет из узлов (в котором допустимы все 5 тайлов) неинтересен для алгоритма WFC, потому что нельзя попасть в ситуацию, когда невозможно разместить тайл. Мы называем тайлсеты с таким свойством «простыми». Без сложных эвристик простые тайлсеты не создают интересных глобальных структур, потому что корреляции в простых тайлсетах на расстоянии быстро снижаются. Множество простых тайлетов можно найти на сайте cr31. Посмотрите там на двухсторонний тайлсет «Dual». Как он может создавать узлы (без Т-образных соединений, то есть непростые), в то же время будучи простым? Ответ заключается в том, что он может генерировать только узкий тип узлов и не может создавать произвольный узел.

Стоит также заметить, что тайлсеты Circuit, Summer и Rooms не являются плитками Вана. То есть данные их соседства нельзя породить из расцветки краёв. Например, в тайлсете Circuit (интегральная схема) два уголка (Corner) не могут быть соседними, хотя и могут соединяться тайлом (Connection), а диагональные дорожки не могут менять направления.

Более высокие размерности

Алгоритм WFC в более высоких размерностях работает совершенно так же, как и в двух измерениях, однако здесь проблемой становится производительность. Эти воксельные модели генерировались при N=2 в тайловой модели с перекрытием при помощи блоков 5x5x5 и 5x5x2 и дополнительных эвристик (высоты, плотности, кривизны...).

Скриншоты более высоких размерностей: 1, 2, 3.

Сгенерированные с помощью WFC и других алгоритмов воксельные модели будут находиться в отдельном репозитории.

Синтез с ограничениями

Алгоритм WFC поддерживает ограничения. Поэтому его с лёгкостью можно комбинировать с другими генеративными алгоритмами или ручным созданием.

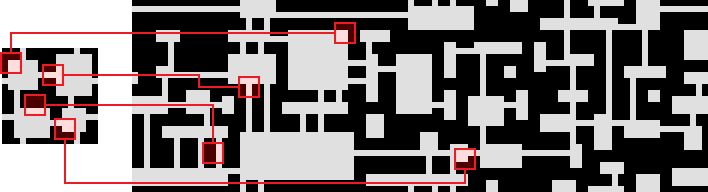
Вот, как WFC автоматически завершает уровень, начатый человеком:

GIF | GIFV

Алгоритм ConvChain удовлетворяет строгой версии условия (C2): создаваемое им распределение пределов паттернов NxN в выходных данных точно такое же, как распределение паттернов во входных данных. Однако ConvChain не удовлетворяет (C1): часто он создаёт заметные артефакты. Логично сначала запускать ConvChain, чтобы получать хорошо сэмплированную конфигурацию, а затем WFC для коррекции локальных артефактов. Это похоже на распространённую в оптимизации стратегию: сначала выполняем метод Монте-Карло для нахождения точки. близкой к глобальному оптимуму, а затем выполняем из этой точки градиентный спуск для большей точности.

Алгоритм синтеза текстур П. Ф. Харрисона значительно быстрее, чем WFC, но у него возникают проблемы с длинными корреляциями (например, этому алгоритму сложно синтезировать текстуры кирпичных стен с правильно выстроенными кирпичами). Именно в таких случаях WFC демонстрирует своё превосходство, а алгоритм Харрисона поддерживает ограничения. Имеет смысл сначала сгенерировать с помощью WFC идеальную схему кирпичной стены, а затем выполнить для этой схемы алгоритм ограниченного синтеза текстур.

Комментарии

Почему используется эвристика минимальной энтропии? Я заметил, что когда люди что-то рисуют, они часто сами следуют эвристике минимальной энтропии. Именно поэтому за алгоритмом так интересно наблюдать.

Модель с перекрытием соотносится с простой моделью так же, как цепи Маркова высокого порядка соотносятся с цепями Маркова первого порядка.

Нужно учесть, что энтропия любого узла не может увеличиваться на этапе распространения, т.е. вероятности не повышаются, но могут быть обнулены. Когда этап распространения не может дальше уменьшать энтропию, мы активируем этап наблюдения. Если этап наблюдения не может уменьшить энтропию, это значит, что алгоритм закончил работу.

Этап распространения в алгоритме WFC очень похож на цикличный алгоритм передачи сообщений (loopy belief propagation algorithm). На самом деле, я изначально программировал belief propagation (BP), но затем перешёл к распространению с ограничениями с сохраненённым стационарным распределением, потому что BP значительно медленнее без массивной параллелизации (в ЦП) и он не создавал значительно лучших результатов для моих задач.

Заметьте, что сэмплы «Simple Knot» и «Trick Knot» имеют не 2, а 3 цвета.

Одним из измерений может быть время. В частности, d-мерный WFC отображает поведение любого (d-1)-мерного клеточного автомата.

Справочные материалы

Этот проект основан на работе Пола Меррелла по синтезу моделей, в частности, на главе о дискретном синтезе моделей из его диссертации. Пол распространяет ограничения соседства в том, что мы назвали простой тайловой моделью, с эвристикой, стремящейся вычислить распространение в небольшой подвижной области.

Также на мой проект сильно повлияла глава о декларативном синтезе текстур из диссертации Пола Ф. Харрисона. Пол задаёт данные о соседстве тайлов, помечая их границы и используя поиск в возвратом для заполнения тайловой карты.

Сборка

WFC — это консольное приложение, зависящее только от стандартной библиотеки. Скачайте .NET Core для Windows, Linux или macOS и выполните

dotnet run WaveFunctionCollapse.csproj

Или же можно использовать инструкции сообщества по сборке для разных платформ в соответствующем issue. Кейси Маршалл создал pull request, который упрощает использование программы с командной строкой и включает пакет snap.

Интересные порты, форки и спин-оффы

• Эмиль Эрнерфельд создал порт на C++.
• Макс Эллер создал библиотеку Kotlin (JVM) под названием Kollapse. Джозеф Роскопф создал построчный порт на Kotlin оптимизированной версии алгоритма 2018 года. Эдвин Джейкобс создал ещё одну библиотеку Kotlin.
• Кевин Чапельер создал порт на JavaScript.
• Оскар Сталберг запрограммировал трёхмерную тайловую модель, двухмерную тайловую модель для неравномерных сеток в сфере. Вот красивые 3D-тайлсеты для них: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.
• Джозеф Паркер адаптировал WFC под Unity и использовал его для генерации скейтпарков в игре Proc Skater 2016, фантастических плато в игре 2017 года Swapland и платформенных уровней в игре 2018 года Bug with a Gun.
• Мартин О'Лири применил напоминающий WFC алгоритм для генерации поэзии: 1, 2, 3, 4.
• Ник Ненов создал трёхмерный воксельный тайлсет, основанный на моём тайлсете Castle. Ник использует опцию текстового вывода данных в тайловую модель для воссоздания 3D-моделей в Cinema 4D.
• Шон Лефлер реализовал модель с перекрытием на Rust.
• rid5x создаёт версию WFC на OCaml.
• Я опубликовал простую трёхмерную тайловую модель, чтобы люди могли создавать собственные 3D-тайлсеты, не ожидая полного репозитория трёхмерного алгоритма.
• Я создал интерактивную модель модели с перекрытием. Исполняемый файл с GUI можно скачать страницы WFC на itch.io.
• Брайан Баклью собрал конвейер генерации уровней для игры Caves of Qud, в нескольких проходах которого используется WFC: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.
• Дэнни Уайн реализовал трёхмерную тайловую модель.
• Арви Теикари запрограммировал алгоритм синтеза текстур с энтропийной эвристикой на Lua. Headchant портировал его для работы с LÖVE.
• Айзек Кэрт создал порт на Python модели с перекрытием.
• Оскар Сталберг создал интерактивную версию тайловой модели, запускаемую в браузере.
• Мэтт Рикс реализовал трёхмерную тайловую модель (1, 2, 3, 4) и создал трёхмерную тайловую модель, в которой одним из измерений является время (1, 2, 3, 4, 5).
• Ник Ненов создал визуальное руководство по системе симметрии тайлов.
• Айзек Кэрт и Адам М. Смит написали исследовательскую статью, в которой они формулируют WFC как ASP-задачу, используют обобщённый решатель общих ограничений clingo для генерации битовых изображений, экспериментируют с глобальными ограничениями, прослеживают историю WFC и дают подробное описание алгоритма.
• Силвэн Лефевр создал реализацию на C++ синтеза трёхмерных моделей, описал мыслительный процесс создания сэмпла и показал пример, в котором ограничения соседства гарантируют, что выходные данные соединены (их можно обойти).
• Я обобщил трёхмерный WFC, чтобы он работал с группой симметрии куба и создал тайлсет, генерирующий сцены в духе Эшера.
• Существует множество способов визуализации частично наблюдаемых волновых состояний. В коде цветовые значения возможных вариантов усреднены для получения конечного цвета. Оскар Сталберг показывает частично наблюдаемые состояния как полупрозрачные прямоугольники: чем больше вариантов, тем больше прямоугольник. В воксельной схеме я визуализирую волновые состояния попиксельным голосованием.
• Реми Дево реализовал тайловую модель в PICO-8 и написал статью о генерации когерентных данных с объяснением WFC.
• Для своей игры Bad North Оскар Сталберг использует эвристику, которая пытается выбрать такие тайны, чтобы на каждом этапе получившаяся наблюдаемая зона была проходимой.
• Уильям Мэннинг реализовал модель с перекрытием на C#; в первую очередь он стремился сделать код читаемым, и дополнил WPF графическим интерфейсом.
• Джозеф Паркер написал туториал по WFC для Procjam 2017.
• Аман Тивари сформулировал ограничение соединения как ASP-задачу для clingo.
• MatveyK запрограммировал трёхмерную модель с перекрытием.
• Силвэн Лефевр, Ли Ю Вей и Коннелли Барнс исследуют возможность сокрытия информации внутри текстур. Они создали инструмент, способный кодировать текстовые сообщения как тайлы WFC и декодировать их обратно. Эта техника позволяет использовать тайлы WFC как QR-коды.
• Матьё Фер и Натаниэль Куран значительно улучшили время выполнения WFC, для модели с перекрытием — на порядок величин. Я интегрировал их усовершенствования в код.
• Васу Махеш портировал трёхмерную тайловую модель в TypeScript, создал новый тайлсет и визуализировал процесс генерации в WebGL.
• Ким Хуанхи экспериментировал с трёхмерным WFC и создал/адаптировал множество воксельных тайлсетов: 1, 2, 3, 4, 5, 6, 7, 8.
• Оскар Сталберг выступил с докладом о генерации уровней в Bad North на конференции Everything Procedural Conference 2018.
• Я написал о том, как генерировать (приближенно) неискажённые пути между двумя точками с помощью WFC и других алгоритмов.
• Айзер Кэрт и Адам М. Смит опубликовали препринт, в котором описывают основанную на WFC систему, которая учится на положительных и отрицательных примерах, и рассказали о ней в общем контексте диалогов с генераторами, работающими на основе примеров.
• Брэндан Энтони использует WFC для генерации украшений стен в игре Rodina.
• Тим Конг реализовал модель с перекрытием на Haxe.
• Для генерации соединённых структур Boris the Brave применил к WFC метод рыхления (chiseling method). Он опубликовал библиотеку, поддерживающую сетки из шестиугольников, дополнительные ограничения и возврат назад.
• Мариан Кляйнеберг создал для Procjam 2018 генератор городов, основанный на тайловой модели. Он написал статью, описывающую свои подходы к заданию соседства, возврату назад и онлайн-вариации WFC.
• Сол Бекич запрограммировал с помощью PyOpenCL тайловую модель, выполняемую на GPU. Вместо хранения очереди узлов, из которых выполняется распространение, эта модель параллельно выполняет распространение из каждого узла сетки.
• Воутер ван Оортмерссен реализовал тайловую модель в единственной функции C++ со структурой для ускорения наблюдения, похожей на очередь с приоритетами.
• Роберт Хёниг реализовал модель с перекрытием на Julia с опцией распространения ограничений только локально.
• Эдвин Джейкобс применил WFC к переносу стиля и дизерингу.

Благодарности

Часть примеров взята из игр Ultima IV и Dungeon Crawl. Тайлсет Circles взят у Марио Клингеманна. Идея генерации интегральных схем была предложена Moonasaur, а их стиль был взять из игры Ruckingenur II компании Zachtronics. Пример с перекрытием Cat взят из видео Nyan Cat, пример Qud был создан Брайаном Баклью, примеры Magic Office + Spirals — rid5x, примеры с перекрытием Colored City + Link + Link 2 + Mazelike + Red Dot + Smile City — Арви Теикари. Тайлсет Summer был создан Германном Хиллманном. Воксельные модели отрендерены в MagicaVoxel.

Автор: PatientZero

Источник