Всем привет! Меня зовут Гриша, и я основатель CGDevs. Математика – очень крутой инструмент при разработке игр. Но если скажем без понимания векторов и матриц обойтись в принципе сложно, то алгоритмы триангуляций не столь обязательная вещь, но с помощью них решается достаточно большое количество интересных задач. Сегодня хотелось бы поговорить про достаточно важный инструмент в вычислительной геометрии, такой как триангуляции и их применение в игровой индустрии. Кроме того, я написал порт и немного обёрток великолепной библиотеки Triangle.Net для Unity + поделиться парой своих реализаций алгоритмов триангуляции. Если интересно – добро пожаловать под кат. Ссылка на гитхаб прилагается.

Что такое триангуляция?
В общем случае триангуляция – это разбиение геометрического объекта на треугольники. Это понятие само по себе довольно простое. Базовый пример триангуляции в случае игровых движков – это меш. Строго говоря меш может состоять не только из треугольников, но в игровых движках по целому ряду причин берутся именно меши, состоящие из треугольников.
Триангуляции бывают разными, но один из самых популярных видов триангуляций является триангуляция Делоне. Этот вид триангуляции отличается тем свойством, что в окружности, описанной вокруг каждого треугольника, лежат только вершины этого треугольника.

Зачем они нужны?
В целом за пределами игровой индустрии с помощью триангуляций решается большое количество задач. В геймдеве же первая задача, которая приходит на ум – это navigation mesh. Навмеш – это структура данных, которая определяет, по какому пространству игрок может ходить. Он позволяет избежать таких сложных вычислительных задач, как определение столкновений с частью окружения.
Вторая интересная задача, решаемая с помощью триангуляции Делоне в геймдеве – это генерация террейнов и объектов представленных в виде множества точек. Основным плюсом триангуляции Делоне в данном случае является то, что исходя из её свойств она позволяет избежать очень острых треугольников, которые будут мешать и создавать артефакты на тиррейне.

Помимо этого, с помощью триангуляции Делоне с ограничениями и таким алгоритмам как Chew's second algorithm и Ruppert's algorithm можно генерировать сетки ещё лучше для тиррейнов и генерировать хорошие сетки для другого применения – метода конечных элементов.
Сам по себе метод конечных элементов, это один из методов с помощью которого решаются задачи прикладной физике. В геймдеве он позволяет решать многие задачи, связанные с симуляцией деформаций, жидкостных симуляций и другого используемого для спец. эффектов. Обычно для записи эффектов в анимации, так как для реалтайма метод обладает слишком высокой вычислительной сложностью. Важной деталью при использовании метода является то, что ошибка метода зависит от углов треугольников в сетке. При наличии в сетке очень острых углов метод даёт огромную ошибку, по этой причине нужны алгоритмы, перечисленные выше.
Ну и конечно же в целом процедурная генерация мешей. Как пример в гитхаб проекте приведена сцена с возможностью рисовать меши. Некоторые физические головоломки используют это применение, как основную механику. Но кроме того алгоритмы триангуляции позволяют с помощью процедурной генерации решать такие задачи, как процедурная разрушаемость и прочее.
Помимо геймдева триангуляции используются в сетях, компьютерном зрении, различных аналитических алгоритмах, а так же в каких задачах вычислительной геометрии, как объединение и исключение многоугольников друг из друга (что бывает полезно часто и в задачах возникающих при разработке игр)
Ear Clipping with Holes
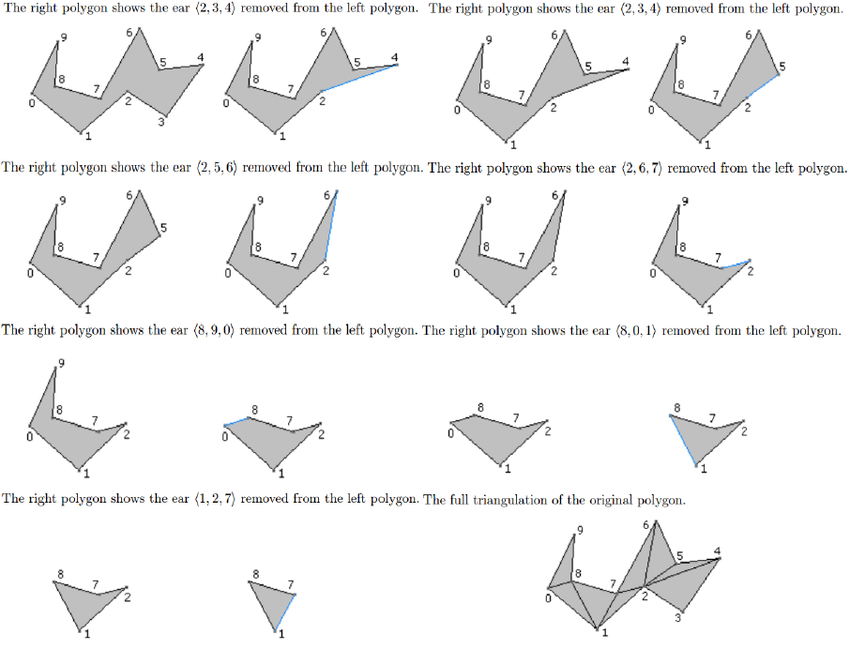
Пожалуй, один из самых простых алгоритмов триангуляции. Даёт не лучшую сетку и обладает большой вычислительной сложностью О(n^2) в худшем случае.
Подробнее про него можно прочитать в этой статье
Bowyer–Watson algorithm
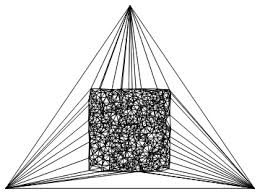
Алгоритм, генерирующий триангуляцию Делоне по набору точек. В целом, как и у большинства алгоритмов Делоне при правильной реализации алгоритмическая сложность O( n log n), где n – количество вершин. Но в некоторых случаях может занимать O(n^2).
Минусами относительно Ear Clipping является то, что данный алгоритм строит выпуклую триангуляцию и в базовой реализации не предполагает дыр в получившейся сетке.
Обработка триангуляции Делоне (Delaunay refinement)
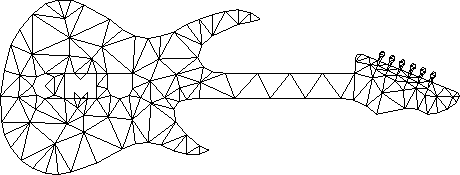
Chew's second algorithm и Ruppert's algorithm – это алгоритмы, которые позволяют вводить ограничения в триангуляцию Делоне и задать минимальный угол треугольника в сетке. Важной деталью алгоритмов является то, что они могут уйти в бесконечный цикл и гарантировано дают результат при углах между примерно 20.7 градусов и 29 градусов. Возможность задать минимальный угол важна при решении задач, описанных выше.
Chew’s second algorithm реализован в бесплатном пакете www.cs.cmu.edu/~quake/triangle.html и его порте на .Net archive.codeplex.com/?p=triangle
Triangle.Net для Unity
Ну и раз уж с помощью триангуляций можно решать так много крутых задач, то на праздниках захотелось реализовать свою обёртку для Unity, чтобы всегда иметь под рукой удобный инструмент. В данной реализации алгоритм триангуляции в среднем работает за O(n), а в худшем за O(n * log n) – где n-количество вершин. К примеру, при тесте на 1кк вершин случайно разбросанных по квадрату юнити в редакторе на Intel Core i7-8700 строило сетку в среднем за 7.56 секунд.
Основные отличия от оригинальной библиотеки в наличии методов расширений заточенных под Unity, а так же замена double на float во всей библиотеке (+ пара определённых операторов для каста) Double в юнити не имеет особого смысла. Если считать физические симуляции, то я бы использовал отдельное приложение на плюсовой библиотеке, а результат вычислений уже отдавал Unity чисто для визуализации. А также переименован тип Mesh на TriangleNetMesh, чтобы не сбивать относительно Mesh из Unity. Да, они и так в разных неймспейсах, но тем не менее думаю новичков немного сбивал бы тот факт, что мы с помощью одного Mesh получаем другой.
Суть библиотеки в том, что вы сначала должны задать так называемый полигон. Потом на его основе сгенерировать уже меш. Для того, чтобы это работало с юнитёвыми структурами данных было введено несколько методов расширений.
public void GenerateMesh()
{
if(_CurrentState != MeshDrawerState.Nothing) return;
Polygon poly = new Polygon();
poly.Add(_Contour);
foreach (var hole in _Holes)
{
poly.Add(hole, true);
}
var triangleNetMesh = (TriangleNetMesh) poly.Triangulate();
GameObject go = new GameObject("Generated mesh");
var mf = go.AddComponent<MeshFilter>();
var mesh = triangleNetMesh.GenerateUnityMesh();
mesh.uv = GenerateUv(mesh.vertices);
mf.mesh = mesh;
var mr = go.AddComponent<MeshRenderer>();
mr.sharedMaterial = _MeshMaterial;
var collider = go.AddComponent<PolygonCollider2D>();
collider.points = _Contour.ToArray();
var rb = go.AddComponent<Rigidbody2D>();
rb.mass = triangleNetMesh.Triangles.Sum(tris => tris.Area);
Clear();
}
Для демонстрации и примера использования была сделана специальная демо-сцена с возможностью отрисовки мешей. С ней и портом библиотеки можно ознакомится в github проекте.
Спасибо за внимание! Надеюсь, что порт и статья кому-то будут полезны и стало чуть понятнее, зачем нужны триангуляция и знание математики в целом. Буду стараться продолжать раскрывать применения и способы решения разных математических задач в геймдеве. В самой вычислительной геометрии ещё очень много интересного, но помимо ещё есть множество других интересных разделов высшей математики.
Автор: DyadichenkoGA




