Cтатья написана по анализу и изучению материалов соревнования по поиску корабликов на море.

Попробуем понять, как и что ищет сеть и что находит. Статья эта есть просто результат любопытства и праздного интереса, ничего из нее в практике не встречается и для практических задач тут нет ничего для копипастинга. Но результат не совсем ожидаем. В интернете полно описаний работы сетей в которых красиво и с картинками авторы рассказывают, как сети детерминируют примитивы — углы, круги, усы, хвосты и т.п., потом их разыскивают для сегментирования/классификации. Многие соревнования выигрываются с помощью весов с других больших и широких сетей. Интересно понять и посмотреть как и какие примитивы строит сеть.
Проведем небольшое исследование и рассмотрим варианты — рассуждения автора и код изложены, можно все проверить/дополнить/изменить самим.
Недавно закончились соревнования на kaggle по поиску судов на море. Компания Airbus предлагала провести анализ космических снимков моря как с судами так и без. Всего 192555 картинок 768х768х3 — это 340 720 680 960 байт если uint8 и четыре раза столько если float32 (кстати float32 быстрее float64, меньше обращений к памяти) и на 15606 картинках нужно найти суда. Как обычно, все значимые места заняли люди причастные к ODS (ods.ai), что естественно и ожидаемо и, надеюсь, что скоро сможем изучить ход мыслей и код победителей и призеров.
Мы же рассмотрим похожую задачу, но упростим её существенно — море возьмем np.random.sample()*0.5, нам не нужны волны, ветер, берега и иные скрытые закономерности и лики. Сделаем изображение моря действительно случайным в диапазоне RGB от 0.0 до 0.5. Суда раскрасим тоже в тот же цвет и чтобы отличать от моря поместим в диапазон от 0.5 до 1.0, и все они будут одинаковой формы — эллипсы разного размера и ориентации.

Возьмем очень распространенный вариант сети (вы можете взять свою любимую сеть) и все эксперименты будем делать с ней.
Далее будем менять параметры картинки, создавать помехи и строить гипотезы — так выделим основные признаки, по которым сеть находит эллипсы. Возможно читатель сделает свои выводы и автора опровергнет.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import math
from tqdm import tqdm_notebook, tqdm
from skimage.draw import ellipse, polygon
from keras import Model
from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau
from keras.models import load_model
from keras.optimizers import Adam
from keras.layers import Input, Conv2D, Conv2DTranspose, MaxPooling2D, concatenate, Dropout
from keras.losses import binary_crossentropy
import tensorflow as tf
import keras as keras
from keras import backend as K
from tqdm import tqdm_notebook
w_size = 256
train_num = 8192
train_x = np.zeros((train_num, w_size, w_size,3), dtype='float32')
train_y = np.zeros((train_num, w_size, w_size,1), dtype='float32')
img_l = np.random.sample((w_size, w_size, 3))*0.5
img_h = np.random.sample((w_size, w_size, 3))*0.5 + 0.5
radius_min = 10
radius_max = 30
def dice_coef(y_true, y_pred):
y_true_f = K.flatten(y_true)
y_pred = K.cast(y_pred, 'float32')
y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32')
intersection = y_true_f * y_pred_f
score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f))
return score
def dice_loss(y_true, y_pred):
smooth = 1.
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = y_true_f * y_pred_f
score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
return 1. - score
def bce_dice_loss(y_true, y_pred):
return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred)
def get_iou_vector(A, B):
# Numpy version
batch_size = A.shape[0]
metric = 0.0
for batch in range(batch_size):
t, p = A[batch], B[batch]
true = np.sum(t)
pred = np.sum(p)
# deal with empty mask first
if true == 0:
metric += (pred == 0)
continue
# non empty mask case. Union is never empty
# hence it is safe to divide by its number of pixels
intersection = np.sum(t * p)
union = true + pred - intersection
iou = intersection / union
# iou metrric is a stepwise approximation of the real iou over 0.5
iou = np.floor(max(0, (iou - 0.45)*20)) / 10
metric += iou
# teake the average over all images in batch
metric /= batch_size
return metric
def my_iou_metric(label, pred):
# Tensorflow version
return tf.py_func(get_iou_vector, [label, pred > 0.5], tf.float64)
from keras.utils.generic_utils import get_custom_objects
get_custom_objects().update({'bce_dice_loss': bce_dice_loss })
get_custom_objects().update({'dice_loss': dice_loss })
get_custom_objects().update({'dice_coef': dice_coef })
get_custom_objects().update({'my_iou_metric': my_iou_metric })
Мы используем ставшую классической метрику в сегментации картинок, есть очень много статей, кода с комментариями и текста про выбранную метрику, на том же kaggle есть масса вариантов с коммментариями и пояснениями. Мы будем предсказывать маску пикселя — это «море» или «кораблик» и оценивать истинность или ложность предсказанния. Т.е. возможны следующие четыре варианта — мы правильно предсказали, что пиксель это «море», правильно предсказали, что пиксель это «кораблик» или ошиблись в предсказании «море» или «кораблик». И так по всем картинкам и всем пикселям оцениваем количество всех четырех вариантов и подсчитываем результат — это и будет результат работы сети. И чем меньше ошибочных предсказаний и больше истинных, то тем точнее полученный результат и лучше работа сети.
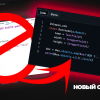
И для проведения исследований возьмем хорошо изученную u-net, это отличная сеть для сегментации картинок. Сеть очень распространена в таких соревнованиях и есть много описаний, тонкости применения и т.д. Выбран вариант классической U-net и, конечно, можно было ее модернизировать, добавить residual блоки и т.д. Но «нельзя объять необъятное» и провести все эксперименты и тесты сразу. U-net производит с картинками очень простую операцию — пошагово уменьшает размерность картинки с некоторыми преобразованиями и после пытается восстановить маску из сжатого изображения. Т.е. размерность картинки в нашем случае доводится до 32x32 и далее пытаемся восстановить маску используя данные со всех предыдущих сжатий.
На картинке схема U-net из оригинальной статьи, но мы её немного переделали, но суть осталась та же — картинку сжимаем → расширяем в маску.
def build_model(input_layer, start_neurons):
conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(input_layer)
conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(conv1)
pool1 = MaxPooling2D((2, 2))(conv1)
pool1 = Dropout(0.25)(pool1)
conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(pool1)
conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(conv2)
pool2 = MaxPooling2D((2, 2))(conv2)
pool2 = Dropout(0.5)(pool2)
conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(pool2)
conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(conv3)
pool3 = MaxPooling2D((2, 2))(conv3)
pool3 = Dropout(0.5)(pool3)
conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(pool3)
conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(conv4)
pool4 = MaxPooling2D((2, 2))(conv4)
pool4 = Dropout(0.5)(pool4)
# Middle
convm = Conv2D(start_neurons*16,(3,3),activation="relu", padding="same")(pool4)
convm = Conv2D(start_neurons*16,(3,3),activation="relu", padding="same")(convm)
deconv4 = Conv2DTranspose(start_neurons * 8, (3, 3), strides=(2, 2), padding="same")(convm)
uconv4 = concatenate([deconv4, conv4])
uconv4 = Dropout(0.5)(uconv4)
uconv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(uconv4)
uconv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(uconv4)
deconv3 = Conv2DTranspose(start_neurons*4,(3,3),strides=(2, 2), padding="same")(uconv4)
uconv3 = concatenate([deconv3, conv3])
uconv3 = Dropout(0.5)(uconv3)
uconv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(uconv3)
uconv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(uconv3)
deconv2 = Conv2DTranspose(start_neurons*2,(3,3),strides=(2, 2), padding="same")(uconv3)
uconv2 = concatenate([deconv2, conv2])
uconv2 = Dropout(0.5)(uconv2)
uconv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(uconv2)
uconv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(uconv2)
deconv1 = Conv2DTranspose(start_neurons*1,(3,3),strides=(2, 2), padding="same")(uconv2)
uconv1 = concatenate([deconv1, conv1])
uconv1 = Dropout(0.5)(uconv1)
uconv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(uconv1)
uconv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(uconv1)
uncov1 = Dropout(0.5)(uconv1)
output_layer = Conv2D(1,(1,1), padding="same", activation="sigmoid")(uconv1)
return output_layer
Первый эксперимент. Самый простой
Первый вариант нашего эксперимента выбран специально для наглядности очень простым — море светлее, суда темнее. Все очень просто и очевидно, выдвигаем гипотезу, что сеть найдет суда/эллипсы без проблем и с любой точностью. Функция next_pair генерирует пару картинка/маска, в которой место, размер, угол поворота выбираются случайно. Далее все изменения будут вноситься в эту функцию — изменение раскраски, формы, помехи и т.д. Но сейчас самый простой вариант, проверяем гипотезу о темных корабликах на светлом фоне.
def next_pair():
p = np.random.sample() - 0.5 # пока не успользуем
# r,c - координаты центра эллипса
r = np.random.sample()*(w_size-2*radius_max) + radius_max
c = np.random.sample()*(w_size-2*radius_max) + radius_max
# большой и малый радиусы эллипса
r_radius = np.random.sample()*(radius_max-radius_min) + radius_min
c_radius = np.random.sample()*(radius_max-radius_min) + radius_min
rot = np.random.sample()*360 # наклон эллипса
rr, cc = ellipse(
r, c,
r_radius, c_radius,
rotation=np.deg2rad(rot),
shape=img_l.shape
) # получаем все точки эллипса
# красим пиксели моря/фона в шум от 0.5 до 1.0
img = img_h.copy()
# красим пиксели эллипса в шум от 0.0 до 0.5
img[rr, cc] = img_l[rr, cc]
msk = np.zeros((w_size, w_size, 1), dtype='float32')
msk[rr, cc] = 1. # красим пиксели маски эллипса
return img, msk
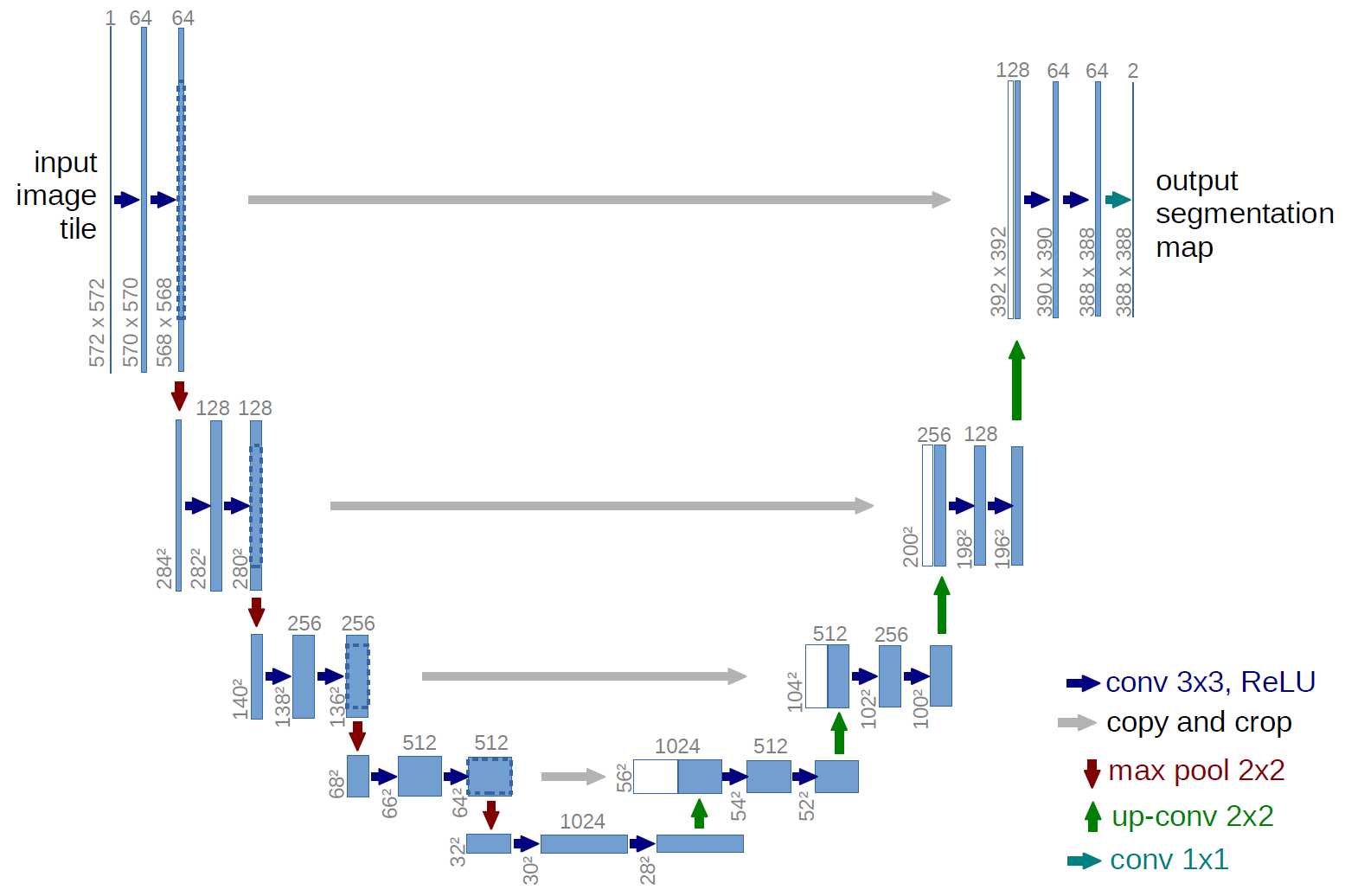
Генерируем весь train и смотрим, что получилось. Вполне похоже на кораблики в море и ничего лишнего. Все хорошо видно, ясно и понятно. Расположение случайное, и на каждой картинке только один эллипс.
for k in range(train_num): # генерация всех img train
img, msk = next_pair()
train_x[k] = img
train_y[k] = msk
fig, axes = plt.subplots(2, 10, figsize=(20, 5)) # смотрим на первые 10 с масками
for k in range(10):
axes[0,k].set_axis_off()
axes[0,k].imshow(train_x[k])
axes[1,k].set_axis_off()
axes[1,k].imshow(train_y[k].squeeze())
Нет никаких сомнений, что сеть обучится успешно и эллипсы найдет. Но проверим нашу гипотезу, что сеть обучается находить эллипсы/кораблики и при этом с высокой точностью.
input_layer = Input((w_size, w_size, 3))
output_layer = build_model(input_layer, 16)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric])
model.save_weights('./keras.weights')
while True:
history = model.fit(train_x, train_y,
batch_size=32,
epochs=1,
verbose=1,
validation_split=0.1
)
if history.history['my_iou_metric'][0] > 0.75:
break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.2272 - my_iou_metric: 0.7325 - val_loss: 0.0063 - val_my_iou_metric: 1.0000
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0090 - my_iou_metric: 1.0000 - val_loss: 0.0045 - val_my_iou_metric: 1.0000
Сеть успешно находит эллипсы. Но совсем не доказано, что она ищет эллипсы в понимании человека, как область ограниченная уравнением эллипса и заполненная отличным от фона содержанием, нет никакой уверенности в том, что найдутся веса сети похожие на коэффициенты квадратного уравнения эллипса. И очевидно, что яркость эллипса меньше яркости фона и никакого секрета и загадки — будем считать, что просто проверили код. Поправим очевидный лик, сделам фон и цвет эллипса тоже случайными.
Второй вариант
Теперь те же эллипсы на таком же море, но цвет моря и, соответственно, кораблика выбирается случайно. Если море выбрано темнее, то судно будет светлее и наоборот. Т.е. по яркости группы точек нельзя отпределить находятся они вне эллипса, т.е.море или это точки внутри эллипса. И опять проверим нашу гипотезу, что сеть найдет эллипсы независимо от цвета.
def next_pair():
p = np.random.sample() - 0.5 # это выбор цвета фон/эллипс
r = np.random.sample()*(w_size-2*radius_max) + radius_max
c = np.random.sample()*(w_size-2*radius_max) + radius_max
r_radius = np.random.sample()*(radius_max-radius_min) + radius_min
c_radius = np.random.sample()*(radius_max-radius_min) + radius_min
rot = np.random.sample()*360
rr, cc = ellipse(
r, c,
r_radius, c_radius,
rotation=np.deg2rad(rot),
shape=img_l.shape
)
if p > 0: # если выбрали фон потемнее
img = img_l.copy()
img[rr, cc] = img_h[rr, cc]
else: # если выбрали фон светлее
img = img_h.copy()
img[rr, cc] = img_l[rr, cc]
msk = np.zeros((w_size, w_size, 1), dtype='float32')
msk[rr, cc] = 1.
return img, msk
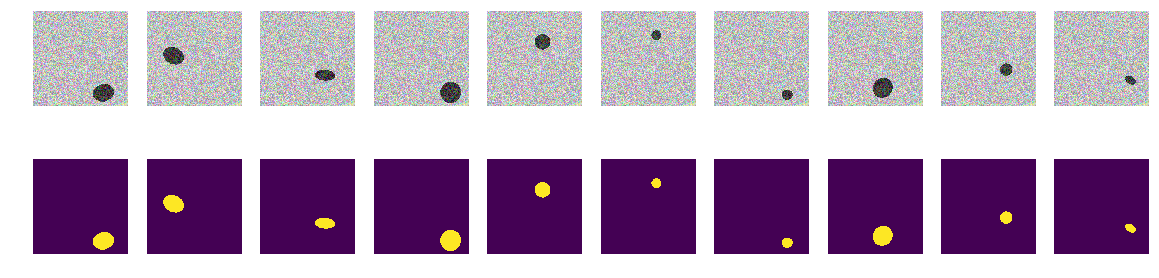
Теперь по пикселю и его окрестности нельзя определить фон это или эллипс. Также проводим генерацию картинок и масок и смотрим на экране первые 10.
for k in range(train_num):
img, msk = next_pair()
train_x[k] = img
train_y[k] = msk
fig, axes = plt.subplots(2, 10, figsize=(20, 5))
for k in range(10):
axes[0,k].set_axis_off()
axes[0,k].imshow(train_x[k])
axes[1,k].set_axis_off()
axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3))
output_layer = build_model(input_layer, 16)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric])
model.load_weights('./keras.weights', by_name=False)
while True:
history = model.fit(train_x, train_y,
batch_size=32,
epochs=1,
verbose=1,
validation_split=0.1
)
if history.history['my_iou_metric'][0] > 0.75:
break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.4652 - my_iou_metric: 0.5071 - val_loss: 0.0439 - val_my_iou_metric: 0.9005
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.1418 - my_iou_metric: 0.8378 - val_loss: 0.0377 - val_my_iou_metric: 0.9206
Сеть легко справляется и находит все эллипсы. Но и тут в реализации есть изъян, и всё очевидно — меньшая из двух областей на картинке и есть эллипс, другая фон. Возможно это и неверная гипотеза, но всё таки поправим, добавим еще полигон на картинку и того же цвета, что и эллипс.
Третий вариант
На каждой картинке выбираем случайно из двух вариантов цвет моря и добавляем эллипс и прямоугольник оба другого, отличного от цвета моря. Получается то же самое «море», так же раскрашенный «кораблик», но на этой же картинке добавляем прямоугольник того же цвета, что и «кораблик» и также со случайно выбранным размером. Теперь наше предположение сложнее, на картинке два одинаково раскрашенных объекта, но мы выдвигаем гипотезу, что всё равно сеть обучится выбирать правильный объект.
def next_pair():
# выбираем также как и ранее параметры эллипса
p = np.random.sample() - 0.5
r = np.random.sample()*(w_size-2*radius_max) + radius_max
c = np.random.sample()*(w_size-2*radius_max) + radius_max
r_radius = np.random.sample()*(radius_max-radius_min) + radius_min
c_radius = np.random.sample()*(radius_max-radius_min) + radius_min
rot = np.random.sample()*360
rr, cc = ellipse(
r, c,
r_radius, c_radius,
rotation=np.deg2rad(rot),
shape=img_l.shape
)
p1 = np.rint(np.random.sample()*(w_size-2*radius_max) + radius_max)
p2 = np.rint(np.random.sample()*(w_size-2*radius_max) + radius_max)
p3 = np.rint(np.random.sample()*(2*radius_max - radius_min) + radius_min)
p4 = np.rint(np.random.sample()*(2*radius_max - radius_min) + radius_min)
# выбираем параметры прямоугольника/помехи, задаем четыре угла
poly = np.array((
(p1, p2),
(p1, p2+p4),
(p1+p3, p2+p4),
(p1+p3, p2),
(p1, p2),
))
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
in_sc = list(set(rr) & set(rr_p)) # следим за тем, что бы прямоугольник
# не пересекался с эллипсом
# и сдвигаем его в сторону при необходимости
if len(in_sc) > 0:
if np.mean(rr_p) > np.mean(in_sc):
poly += np.max(in_sc) - np.min(in_sc)
else:
poly -= np.max(in_sc) - np.min(in_sc)
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
if p > 0:
img = img_l.copy()
img[rr, cc] = img_h[rr, cc]
img[rr_p, cc_p] = img_h[rr_p, cc_p]
else:
img = img_h.copy()
img[rr, cc] = img_l[rr, cc]
img[rr_p, cc_p] = img_l[rr_p, cc_p]
msk = np.zeros((w_size, w_size, 1), dtype='float32')
msk[rr, cc] = 1.
return img, msk
Так же как и раньше вычисляем картинки и маски и смотрим на первые 10 пар.
for k in range(train_num):
img, msk = next_pair()
train_x[k] = img
train_y[k] = msk
fig, axes = plt.subplots(2, 10, figsize=(20, 5))
for k in range(10):
axes[0,k].set_axis_off()
axes[0,k].imshow(train_x[k])
axes[1,k].set_axis_off()
axes[1,k].imshow(train_y[k].squeeze())

input_layer = Input((w_size, w_size, 3))
output_layer = build_model(input_layer, 16)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric])
model.load_weights('./keras.weights', by_name=False)
while True:
history = model.fit(train_x, train_y,
batch_size=32,
epochs=1,
verbose=1,
validation_split=0.1
)
if history.history['my_iou_metric'][0] > 0.75:
break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 57s 8ms/step - loss: 0.7557 - my_iou_metric: 0.0937 - val_loss: 0.2510 - val_my_iou_metric: 0.4580
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.0719 - my_iou_metric: 0.8507 - val_loss: 0.0183 - val_my_iou_metric: 0.9812
Прямоугольниками сеть запутать не удалось и наша гипотеза подтверждается. На соревновании Airbus у всех, судя по примерам и дискуссии, одиночные суда, да и несколько судов рядом находились достаточно точно. Эллипс от прямоугольника — т.е. судно от домика на берегу, сеть отличает, хоть полигоны и того же цвета, что и эллипсы. Дело значит не в цвете, ведь и эллипс и прямоугольник одинаково случайно раскрашены.
Четвертый вариант
Возможно сеть отличает прямоугольники — поправим, исказим и их. Т.е. сеть легко находит обе замкнутые области независимо от формы и отбрасывает ту из них которая прямоугольник. Это гипотеза автора — проверим её, для чего будем добавлять не прямоугольники, а четырехугольные полигоны произвольной формы. И опять наша гипотеза состоит в том, что сеть отличит эллипс от произвольного четырехугольного полигона такой же раскраски.
Можно конечно влезть во внутренности сети и там смотреть на слои и анализировать смысл весов и сдвигов. Автору интересно результирующее поведение сети, суждение будет строится по результату работы, хотя всегда интересно заглянуть внутрь.
def next_pair():
p = np.random.sample() - 0.5
r = np.random.sample()*(w_size-2*radius_max) + radius_max
c = np.random.sample()*(w_size-2*radius_max) + radius_max
r_radius = np.random.sample()*(radius_max-radius_min) + radius_min
c_radius = np.random.sample()*(radius_max-radius_min) + radius_min
rot = np.random.sample()*360
rr, cc = ellipse(
r, c,
r_radius, c_radius,
rotation=np.deg2rad(rot),
shape=img_l.shape
)
p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min)
p1 = np.rint(np.random.sample()*(w_size-radius_max))
p2 = np.rint(np.random.sample()*(w_size-radius_max))
p3 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p4 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p5 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p6 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p7 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p8 = np.rint(np.random.sample()*2.*radius_min - radius_min)
poly = np.array((
(p1, p2),
(p1+p3, p2+p4+p0),
(p1+p5+p0, p2+p6+p0),
(p1+p7+p0, p2+p8),
(p1, p2),
))
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
in_sc = list(set(rr) & set(rr_p))
if len(in_sc) > 0:
if np.mean(rr_p) > np.mean(in_sc):
poly += np.max(in_sc) - np.min(in_sc)
else:
poly -= np.max(in_sc) - np.min(in_sc)
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
if p > 0:
img = img_l.copy()
img[rr, cc] = img_h[rr, cc]
img[rr_p, cc_p] = img_h[rr_p, cc_p]
else:
img = img_h.copy()
img[rr, cc] = img_l[rr, cc]
img[rr_p, cc_p] = img_l[rr_p, cc_p]
msk = np.zeros((w_size, w_size, 1), dtype='float32')
msk[rr, cc] = 1.
return img, msk
Вычисляем картинки и маски и смотрим первые 10 пар.
for k in range(train_num):
img, msk = next_pair()
train_x[k] = img
train_y[k] = msk
fig, axes = plt.subplots(2, 10, figsize=(20, 5))
for k in range(10):
axes[0,k].set_axis_off()
axes[0,k].imshow(train_x[k])
axes[1,k].set_axis_off()
axes[1,k].imshow(train_y[k].squeeze())

Запускаем нашу сеть. Напомню, что она для всех вариантов одна и та же.
input_layer = Input((w_size, w_size, 3))
output_layer = build_model(input_layer, 16)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric])
model.load_weights('./keras.weights', by_name=False)
while True:
history = model.fit(train_x, train_y,
batch_size=32,
epochs=1,
verbose=1,
validation_split=0.1
)
if history.history['my_iou_metric'][0] > 0.75:
break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.6815 - my_iou_metric: 0.2168 - val_loss: 0.2078 - val_my_iou_metric: 0.4983
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.1470 - my_iou_metric: 0.6396 - val_loss: 0.1046 - val_my_iou_metric: 0.7784
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0642 - my_iou_metric: 0.8586 - val_loss: 0.0403 - val_my_iou_metric: 0.9354
Гипотеза подтверждается, полигоны и эллипсы легко различимы. Внимательный читатель тут отметит — конечно отличаются, ерундовый вопрос, любой нормальный AI может отличить кривую второго порядка от линии первого. Т.е. сеть легко определяет наличие границы в виде кривой второго порядка. Не станем спорить, заменим овал на семиугольник и проверим.
Пятый эксперимент, самый сложный
Нет никаких кривых, только ровные грани правильных наклоненных и повернутых семиугольников и произвольные четырехугольные полигоны. Вснесем в функцию генератор картинок/масок изменения — только проекции правильных семиугольников и произвольные четырехугольные полигоны одного и того же цвета.
def next_pair(_n = 7):
p = np.random.sample() - 0.5
c_x = np.random.sample()*(w_size-2*radius_max) + radius_max
c_y = np.random.sample()*(w_size-2*radius_max) + radius_max
radius = np.random.sample()*(radius_max-radius_min) + radius_min
d = np.random.sample()*0.5 + 1
a_deg = np.random.sample()*360
a_rad = np.deg2rad(a_deg)
poly = [] # строим точки семиугольника
for k in range(_n):
# сначала точки правильного семиугольника
# с_х с_у -координаты центра
poly.append(c_x+radius*math.sin(2.*k*math.pi/_n))
poly.append(c_y+radius*math.cos(2.*k*math.pi/_n))
# сжимаемпроецируем семиугольник
# на произвольную от 0.5 до 1.5 величину
poly[-2] = (poly[-2]-c_x)/d +c_x
poly[-1] = (poly[-1]-c_y) +c_y
# поворачиваем на случайный угол
poly[-2] = ((poly[-2]-c_x)*math.cos(a_rad)
- (poly[-1]-c_y)*math.sin(a_rad)) + c_x
poly[-1] = ((poly[-2]-c_x)*math.sin(a_rad)
+ (poly[-1]-c_y)*math.cos(a_rad)) + c_y
poly = np.rint(poly).reshape(-1,2)
rr, cc = polygon(poly[:, 0], poly[:, 1], img_l.shape)
p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min)
p1 = np.rint(np.random.sample()*(w_size-radius_max))
p2 = np.rint(np.random.sample()*(w_size-radius_max))
p3 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p4 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p5 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p6 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p7 = np.rint(np.random.sample()*2.*radius_min - radius_min)
p8 = np.rint(np.random.sample()*2.*radius_min - radius_min)
poly = np.array((
(p1, p2),
(p1+p3, p2+p4+p0),
(p1+p5+p0, p2+p6+p0),
(p1+p7+p0, p2+p8),
(p1, p2),
))
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
in_sc = list(set(rr) & set(rr_p))
if len(in_sc) > 0:
if np.mean(rr_p) > np.mean(in_sc):
poly += np.max(in_sc) - np.min(in_sc)
else:
poly -= np.max(in_sc) - np.min(in_sc)
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
if p > 0:
img = img_l.copy()
img[rr, cc] = img_h[rr, cc]
img[rr_p, cc_p] = img_h[rr_p, cc_p]
else:
img = img_h.copy()
img[rr, cc] = img_l[rr, cc]
img[rr_p, cc_p] = img_l[rr_p, cc_p]
msk = np.zeros((w_size, w_size, 1), dtype='float32')
msk[rr, cc] = 1.
return img, msk
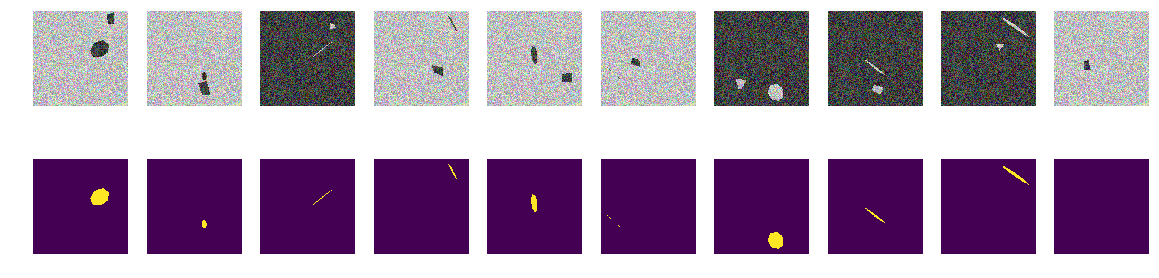
Так же как и раньше строим массивы и смотрим первые 10.
for k in range(train_num):
img, msk = next_pair()
train_x[k] = img
train_y[k] = msk
fig, axes = plt.subplots(2, 10, figsize=(20, 5))
for k in range(10):
axes[0,k].set_axis_off()
axes[0,k].imshow(train_x[k])
axes[1,k].set_axis_off()
axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3))
output_layer = build_model(input_layer, 16)
model = Model(input_layer, output_layer)
model.compile(loss=dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric])
model.load_weights('./keras.weights', by_name=False)
while True:
history = model.fit(train_x, train_y,
batch_size=32,
epochs=1,
verbose=1,
validation_split=0.1
)
if history.history['my_iou_metric'][0] > 0.75:
break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 54s 7ms/step - loss: 0.5005 - my_iou_metric: 0.1296 - val_loss: 0.1692 - val_my_iou_metric: 0.3722
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.1287 - my_iou_metric: 0.4522 - val_loss: 0.0449 - val_my_iou_metric: 0.6833
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0759 - my_iou_metric: 0.5985 - val_loss: 0.0397 - val_my_iou_metric: 0.7215
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0455 - my_iou_metric: 0.6936 - val_loss: 0.0297 - val_my_iou_metric: 0.7304
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0432 - my_iou_metric: 0.7053 - val_loss: 0.0215 - val_my_iou_metric: 0.7846
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0327 - my_iou_metric: 0.7417 - val_loss: 0.0171 - val_my_iou_metric: 0.7970
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0265 - my_iou_metric: 0.7679 - val_loss: 0.0138 - val_my_iou_metric: 0.8280
Итоги
Как видим, сеть различает проекции правильных семиугольников и произвольные четырехугольные полигоны с точностью 0.828 на тестовом множестве. Обучение сети остановлено произвольным значением в 0.75 и скорее всего точность должна быть гораздо лучше. Если исходить из тезиса, что сеть находит примитивы и их комбинации определяют объект, то в нашем случае есть две области с отличающимся своим средним от фона, нет тут никаких примитивов в понимании человека. Линий явных, одноцветных нет, и углов, соответственно, нет, только области с очень похожими границами. Даже если построить линии, то оба объекта на картинке строятся из одинаковых примитивов.
Вопрос знатокам — что же сеть считает признаком по которому отличает «кораблики» от «помехи»? Очевидно, что это не цвет и не форма границ корабликов. Можно конечно дальше продолжить изучение этой абстрактной конструкции «море»/«кораблики», мы не Академия Наук и можем проводить исследования исключительно из любопытства. Можем поменять семиугольники на восьмиугольники или заполнить картинку правильными пяти и шести угольниками и смотреть — отличит их сеть или нет. Оставляю это для читателей — хотя мне тоже стало интересно, может ли сеть считать количество углов полигона и для теста расположить на картинке не правильные многоугольнники, а их случайные проекции.
Есть и другие, не менее интересные свойства таких корабликов, и такие эксперименты полезны тем, что все вероятностные характеристики исследуемого множества задаем мы сами и неожиданное поведение хорошо изученных сетей добавит знание и принесет пользу.
Фон выбран случайным, цвет выбран случайным, место кораблика/эллипса выбрано случайным. На картинках нет линий, есть области с разными характеристиками, но нет одноцветных линий! В данном случае конечно есть упрощения и задачу можно еще усложнить — например выбрать цвета так 0.0… 0.9 и 0.1… 1.0 — но для сети нет никакой разницы. Сеть может и находит закономерности, отличающиеся от тех, что явно видит и находит человек.
Если кто то из читателей заинтересовался, то можете продолжить исследования и ковыряния в сетях, если что не получается или не ясно или вдруг новая и хорошая мысль появится и поразит своей красотой, то Вы всегда можете поделиться с нами или спросить мастеров (и грандмастеров тоже) и попросить квалифицированной помощи в сообществе ODS.
Автор: ChePeter