Если вы не знаете, что такое цветовая температура, начните отсюда.
Работая над инструментом «Цветовая температура» для PhotoDemon, я целый вечер пытался определить простой и понятный алгоритм преобразования между значениями температуры (в Кельвинах) и RGB. Я думал, что такой алгоритм будет просто найти, ведь во многих фоторедакторах есть инструменты для коррекции цветовой температуры, а в каждой современной камере, включая смартфоны, есть регулировка баланса белого на основе условий освещения.
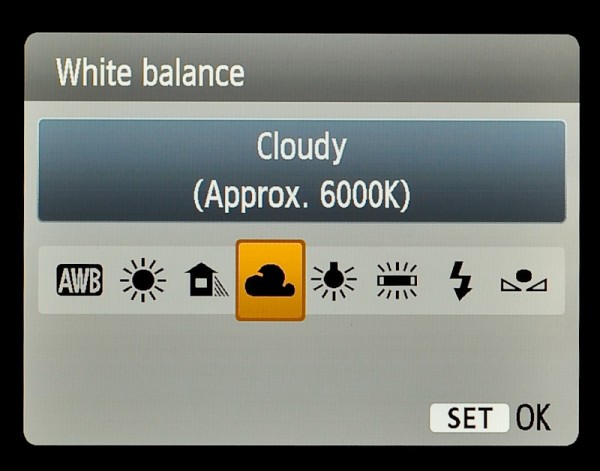
Пример экрана камеры с установкой баланса белого. Источник
Оказалось, найти надёжную формулу преобразования температуры в RGB практически невозможно. Конечно, есть некоторые алгоритмы, но большинство из них работают путём преобразования температуры в цветовое пространство XYZ, к которому вы потом можете добавить преобразование RGB. Такие алгоритмы, похоже, основаны на методе Робертсона, одна реализация которого здесь, а другая здесь.
К сожалению, такой подход не даёт чисто математической формулы — это просто интерполяция по таблице преобразования. Это может быть разумно при определённых обстоятельствах, но если учесть дополнительное преобразование XYZ → RGB, то получается слишком медленно для простой регулировки цветовой температуры в реальном времени.
Поэтому я написал собственный алгоритм, и он работает чертовски хорошо. Вот как у меня это получилось.
Предупреждения относительно этого алгоритма
Предупреждение 1: мой алгоритм обеспечивает высококачественное приближение, но он недостаточно точен для серьёзного научного использования. Он предназначен в основном для манипуляций с фотографиями — так что не пытайтесь использовать его для астрономии или в медицине.
Предупреждение 2: из-за своей относительной простоты этот алгоритм достаточно быстр для работы в реальном времени на изображениях разумного размера (я тестировал его на 12-мегапиксельных снимках), но для достижения наилучших результатов следует применить математические оптимизации, характерные для вашего языка программирования. Я показываю алгоритм без математических оптимизаций, чтобы не усложнять его.
Предупреждение 3: алгоритм предназначен только для использования в диапазоне от 1000 K до 40000 K, что является хорошим диапазоном для фотографии. (На самом деле он намного больше, чем может потребоваться в большинстве ситуаций). Хотя он работает для температур и за пределами этого диапазона, но качество будет снижаться.
Особая благодарность Митчеллу Чарити
Во-первых, должен отдать большой долг и поблагодарить Митчелла Чарити за исходные данные, которые использовал для создания этих алгоритмов: необработанный файл чёрного тела. Чарити предоставляет два набора данных, и мой алгоритм использует 10-градусную функцию сопоставления цветов CIE 1964. Обсуждение 2-градусной функции CIE 1931 с исправлениями Джадда Воса по сравнению с 10-градусным набором выходит за рамки этой статьи, но если вам интересно, можете начать всесторонний анализ с этой страницы.
Алгоритм: пример выдачи
Вот выдача алгоритма в диапазоне от 1000 К до 40000 К:

Выдача моего алгоритма от 1000 К до 40000 К. Белая точка находится на 6500−6600 К, что идеально подходит для обработки фотографий на современном ЖК-мониторе
Вот более подробный снимок алгоритма в интересном для фотографии диапазоне от 1500 К до 15000 К:

Тот же алгоритм, но от 1500 K до 15000 K
Как можно заметить, бандажирование полосами минимально, что является большим улучшением по сравнению с вышеупомянутыми таблицами соответствия. Алгоритм также делает большую работу по сохранению светло-жёлтого оттенка возле белой точки, что важно для имитации дневного света в постобработке фотографий.
Как я пришёл к этому алгоритму
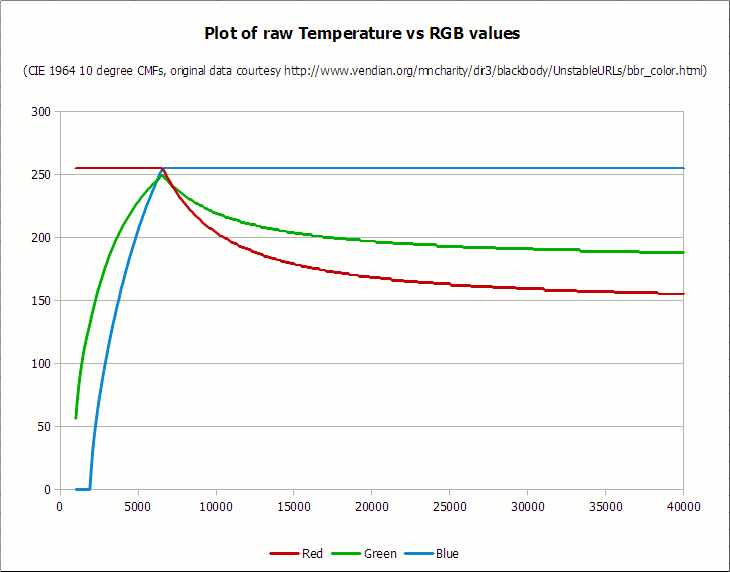
Первым шагом к выведению надёжной формулы было построить график оригинальных значений чёрного тела от Чарити. Вы можете скачать всю электронную таблицу в формате LibreOffice/OpenOffice .ods (430 КБ).
Вот данные после построения графика:
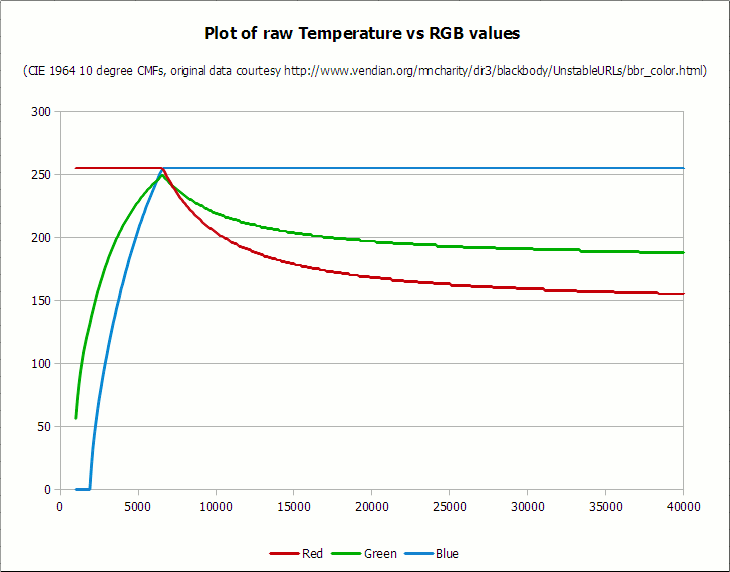
Данные оригинальной температуры (K) в RGB (sRGB), график LibreOffice Calc. Опять же, преобразование основано на 10-градусной CMF-функции CIE 1964. Белая точка, как и требовалось, находится между 6500 K и 6600 K (пик в левой части графика). Источник
Легко заметить, что есть несколько участков, которые упрощают наш алгоритм. В частности:
- Красные значения ниже 6600 K всегда 255
- Синие значения ниже 2000 K всегда 0
- Синие значения выше 6500 K всегда 255
Ещё важно отметить, что для подгонки кривой под данные зелёный цвет лучше всего рассматривать как две отдельные кривые — одна для температур ниже 6600 K, а другая для температур выше этой точки.
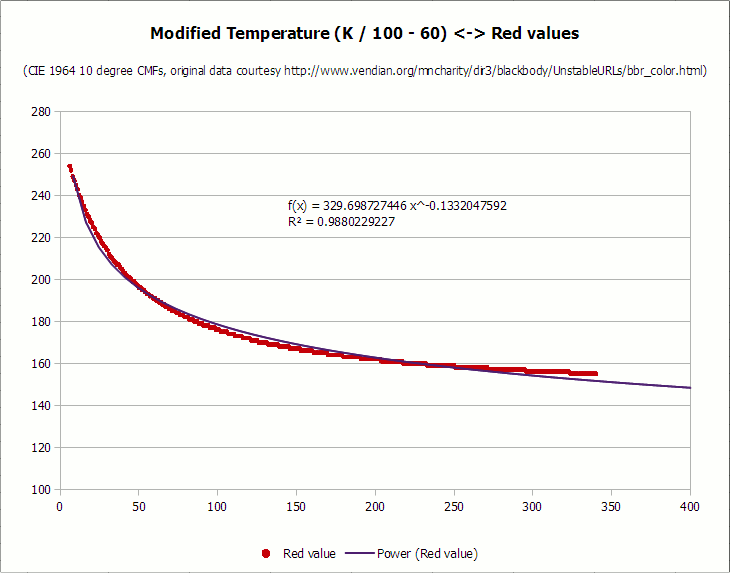
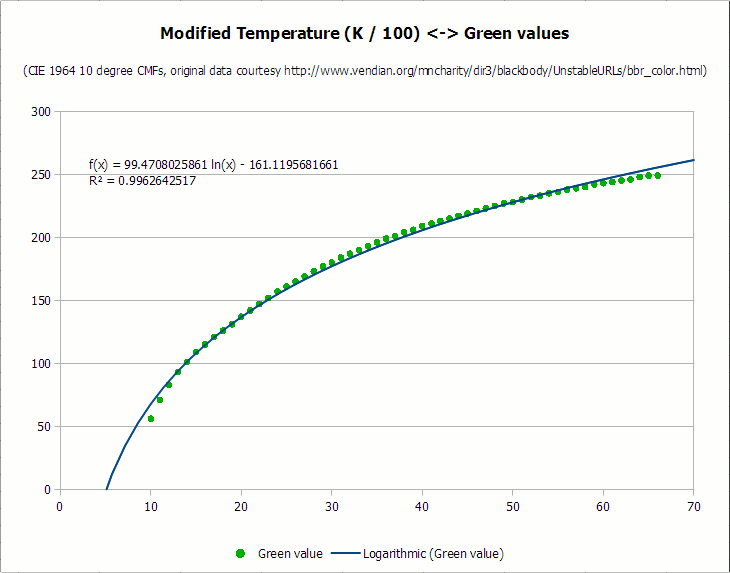
С этого момента я разделил данные (без сегментов «всегда 0» и «всегда 255») на отдельные цветовые компоненты. В идеальном мире кривую можно подогнать к каждому набору точек, но, к сожалению, в реальности это не так просто. Поскольку на графике сильное несоответствие между значениями X и Y — все значения x больше 1000 и отображаются в 100 точечных сегментах, в то время как значения y находятся между 255 и 0 — пришлось транспонировать данные x, чтобы получить лучшее соответствие. В целях оптимизации я сначала разделил значение x (температура) на 100 для каждого цвета, а затем вычел сколько нужно, если это значительно помогало в подгонке к графику. Вот результирующие диаграммы для каждой кривой, а также наиболее подходящая кривая и соответствующее значение коэффициента детерминации (R-квадрат):
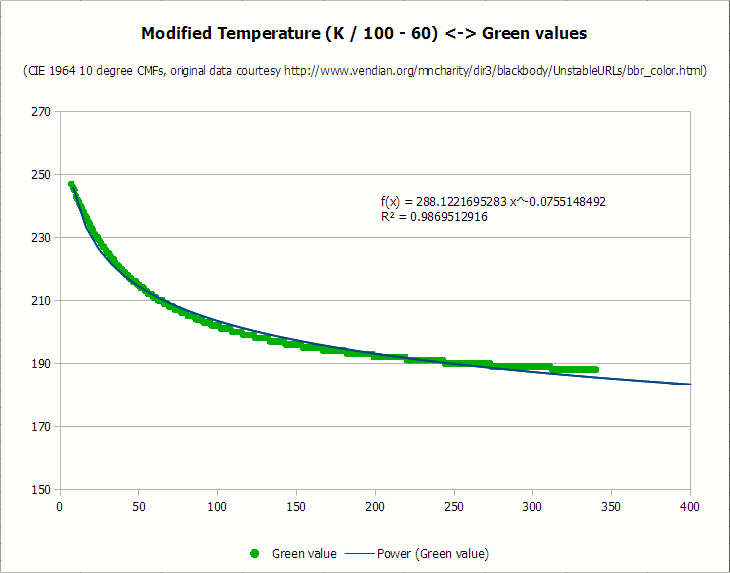
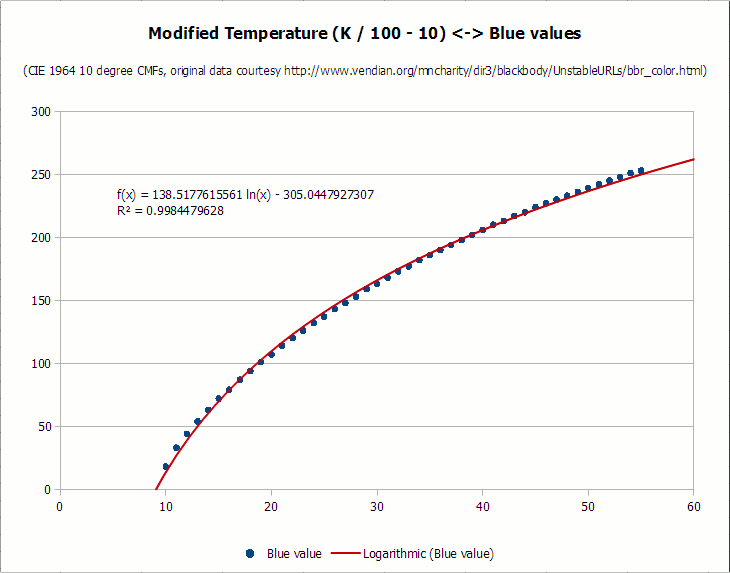
Прошу прощения за ужасный кернинг шрифтов и хинтинг на диаграммах. У LibreOffice много плюсов, но неспособность сглаживать шрифты на графиках совершенно постыдна. Мне также не нравится извлекать диаграммы из скриншотов, потому что у них нет опции экспорта, но это лучше оставить на потом.
Как видите, все кривые достаточно хорошо выровнены, со значениями коэффициента детерминации выше 0,987. Я мог бы потратить больше времени на подгонку кривых, но для обработки фотографиями этого достаточно. Ни один обыватель не скажет, что кривые неточно соответствуют исходным идеализированным наблюдениям чёрного тела, верно?
Алгоритм
Вот алгоритм во всей красе.
Во-первых, псевдокод:
Начнём с температуры в Кельвинах где-то между 1000 и 40000. (Другие значения могут работать, но я не могу дать никаких обещаний о качестве оценок алгоритма выше 40000 K). Обратите внимание, что переменные температуры и цвета должны быть объявлены как переменные с плавающей точкой.
Set Temperature = Temperature 100
Вычисление красного:
If Temperature <= 66 Then
Red = 255
Else
Red = Temperature - 60
Red = 329.698727446 * (Red ^ -0.1332047592)
If Red < 0 Then Red = 0
If Red > 255 Then Red = 255
End If
Вычисление зелёного:
If Temperature <= 66 Then
Green = Temperature
Green = 99.4708025861 * Ln(Green) - 161.1195681661
If Green < 0 Then Green = 0
If Green > 255 Then Green = 255
Else
Green = Temperature - 60
Green = 288.1221695283 * (Green ^ -0.0755148492)
If Green < 0 Then Green = 0
If Green > 255 Then Green = 255
End If
Вычисление синего:
If Temperature >= 66 Then
Blue = 255
Else
If Temperature <= 19 Then
Blue = 0
Else
Blue = Temperature - 10
Blue = 138.5177312231 * Ln(Blue) - 305.0447927307
If Blue < 0 Then Blue = 0
If Blue > 255 Then Blue = 255
End If
End IfОбратите внимание, что в приведённом псевдокоде Ln() означает натуральный логарифм. Также обратите внимание, что можно опустить проверки «если цвет меньше 0», если температуры всегда в рекомендуемом диапазоне. (Однако всё равно нужно оставить проверки «если цвет больше 255»).
Что касается фактического кода, вот точная функция Visual Basic, которую я использую в PhotoDemon. Она ещё не оптимизирована (например, логарифмы стианут намного быстрее с таблицами соответствия), но хотя бы код краткий и читаемый:
'Для данной температуры (в Кельвинах) вычисляем RGB-эквивалент Private Sub getRGBfromTemperature(ByRef r As Long, ByRef g As Long, ByRef b As Long, ByVal tmpKelvin As Long)
Static tmpCalc As Double
'Температура должна быть в диапазоне от 1000 до 40000 градусов
If tmpKelvin < 1000 Then tmpKelvin = 1000
If tmpKelvin > 40000 Then tmpKelvin = 40000
'Все вычисления требуют tmpKelvin 100, так что можно обойтись однократным преобразованием
tmpKelvin = tmpKelvin 100
'Вычисляем все цвета по очереди
'Сначала красный
If tmpKelvin <= 66 Then
r = 255
Else
'Примечание: значение R-квадрата для этого приближения 0,988
tmpCalc = tmpKelvin - 60
tmpCalc = 329.698727446 * (tmpCalc ^ -0.1332047592)
r = tmpCalc
If r < 0 Then r = 0
If r > 255 Then r = 255
End If
'Затем зелёный
If tmpKelvin <= 66 Then
'Примечание: значение R-квадрата для этого приближения 0,996
tmpCalc = tmpKelvin
tmpCalc = 99.4708025861 * Log(tmpCalc) - 161.1195681661
g = tmpCalc
If g < 0 Then g = 0
If g > 255 Then g = 255
Else
'Примечание: значение R-квадрата для этого приближения 0,987
tmpCalc = tmpKelvin - 60
tmpCalc = 288.1221695283 * (tmpCalc ^ -0.0755148492)
g = tmpCalc
If g < 0 Then g = 0
If g > 255 Then g = 255
End If
'Наконец, синий
If tmpKelvin >= 66 Then
b = 255
ElseIf tmpKelvin <= 19 Then
b = 0
Else
'Примечание: значение R-квадрата для этого приближения 0,998
tmpCalc = tmpKelvin - 10
tmpCalc = 138.5177312231 * Log(tmpCalc) - 305.0447927307
b = tmpCalc
If b < 0 Then b = 0
If b > 255 Then b = 255
End If
End SubФункция использовалась для генерации образца выдачи в начале этой статьи, поэтому я могу гарантировать, что она работает.
Примеры изображений
Вот отличный пример того, что могут сделать регулировки цветовой температуры. Изображение ниже — рекламный плакат для сериала HBO «Настоящая кровь» — зрелищно демонстрирует потенциал регулировки цветовой температуры. Слева — исходный кадр; справа — регулировка цветовой температуры с помощью кода выше. Одним щелчком мыши ночную сцену можно переделать для дневного света.
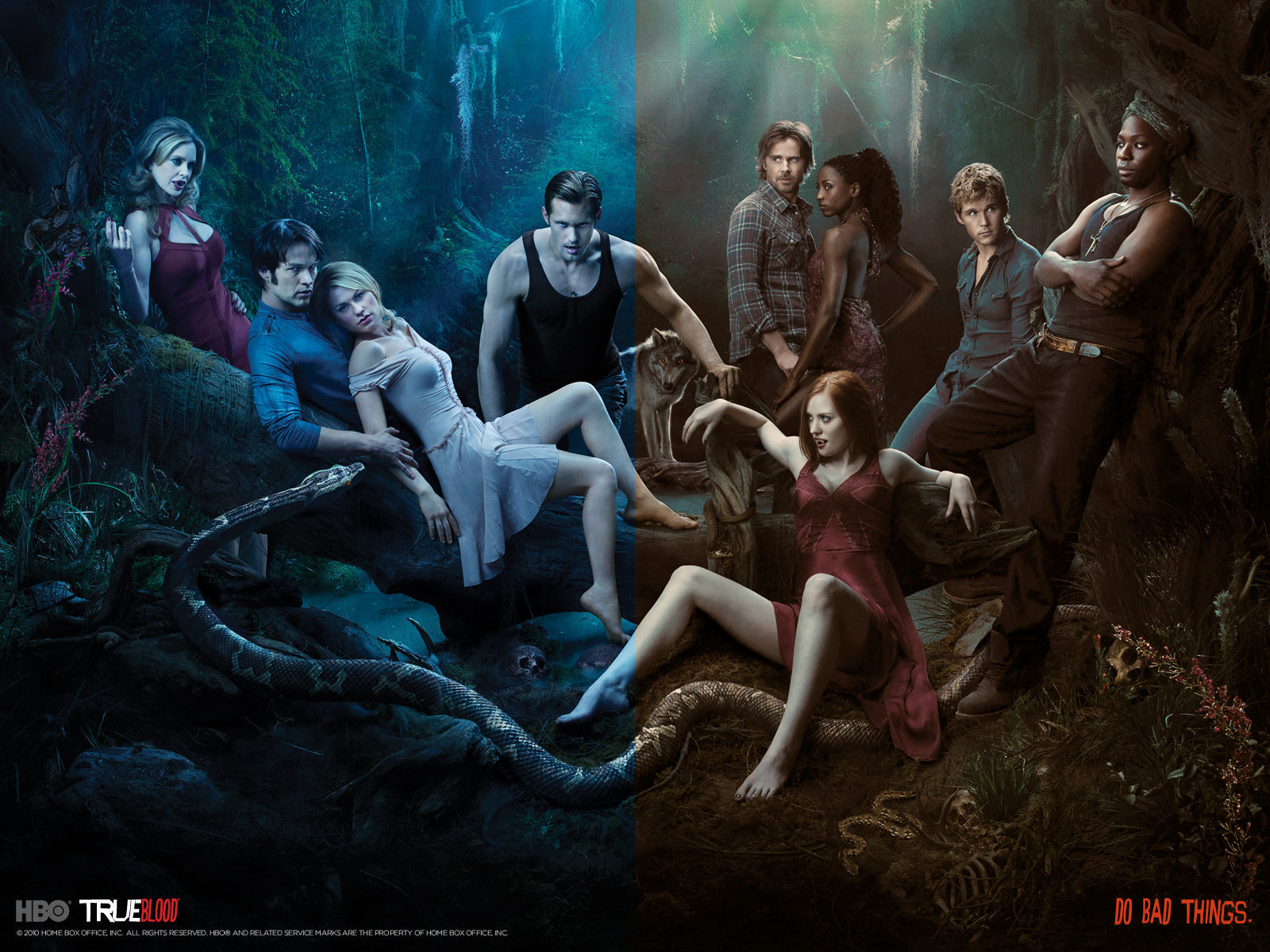
Регулировка цветовой температуры в действии
Реальный инструмент цветовой температуры в моей программе PhotoDemon выглядит следующим образом:
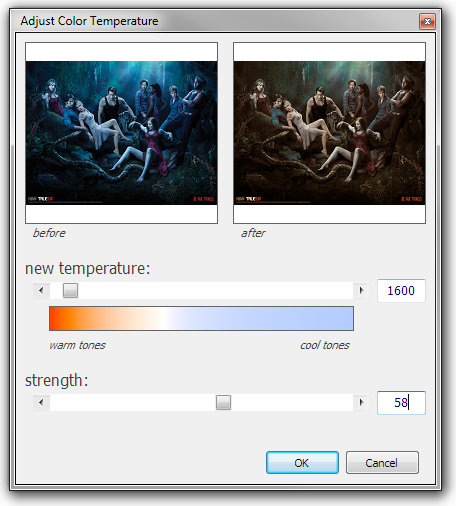
Инструмент цветовой температуры PhotoDemon
Скачайте программу и посмотрите его в действии.
Дополнение, октябрь 2014
Рено Бедар сделал отличное онлайн-демо для этого алгоритма. Спасибо, Рено!
Дополнение, апрель 2015
Спасибо всем, кто предложил улучшения оригинального алгоритма. Я знаю, что у статьи много комментариев, но их стоит прочитать, если вы планируете реализовать собственную версию.
Хочу выделить два конкретных улучшения. Во-первых, Neil B любезно предоставил лучшую версию для исходных функций подгонки кривой, что слегка меняет температурные коэффициенты. Изменения подробно описаны в его превосходной статье.
Затем Фрэнсис Лох добавил некоторые комментарии и примеры изображений, которые очень полезны, если вы хотите применить эти преобразования к фотографиям. Его модификации производят гораздо более детальное изображение, что видно на примерах.
Автор: m1rko