Ричард Хэмминг: Глава 20. Моделирование — III

«Цель этого курса — подготовить вас к вашему техническому будущему.»

Осталось опубликовать 2 главы…

Моделирование — III

Я продолжу общее направление, заданное в предыдущей главе, но на этот раз я сконцентрируюсь на старом выражении «Мусор на входе – мусор на выходе», которое часто сокращают как GIGO (garbage in, garbage out). Идея в том, что если вы поместите неаккуратно собранные данные и неверно определенные выражения на вход, то на выходе вы можете получить только некорректные результаты. Так же неявно предполагается и обратное: из наличия точных входных данных следует и получение корректного результата. Я покажу, что оба эти предположения могут быть ложными.

Часто моделирование строится на решении дифференциальных уравнений, поэтому для начала мы рассмотрим простейшее дифференциальное уравнение первого порядка вида

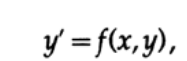
Как вы помните, поле направлений – это построенные в каждой точке плоскости x-y линии, с угловыми коэффициентами, заданными дифференциальным уравнением (Рисунок 20.I). Например, дифференциальное уравнение имеет поле направлений, показанное на рисунке 20.II.

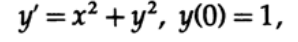
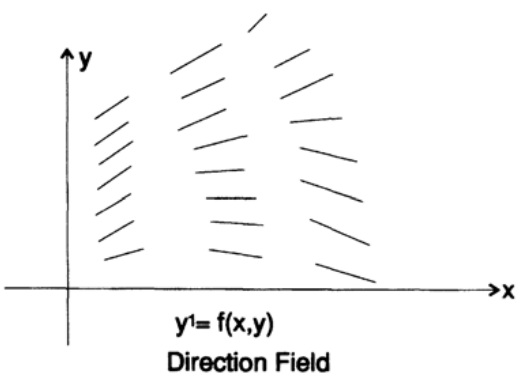
Рисунок 20.I

Для каждой концентрической окружности,

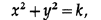
такой что коэффициент наклона прямой всегда одинаковый и зависит от значения k. Такие кривые называются изоклинами.

А теперь посмотрим на поле направлений другого дифференциального уравнения (рисунок 20.III). В левой части мы видим расходящееся поле направлений, это означает что небольшие изменения в начальных значениях или небольшие ошибки вычислений приведут к большой разнице значений в середине траектории. В правой части мы видим, что поле направлений сходится. Это означает, что при большей разнице значений в середине траектории разница значений в правом конце будет небольшой. Этот простой пример показывает, как маленькие ошибки могут становиться большими, большие ошибки маленькими, и более того, как маленькие ошибки могут сначала становится большими, а потом снова маленькими. Поэтому точность решения зависит от конкретного интервала, на котором вычисляется решение. Не существует какой-то абсолютной общей точности.

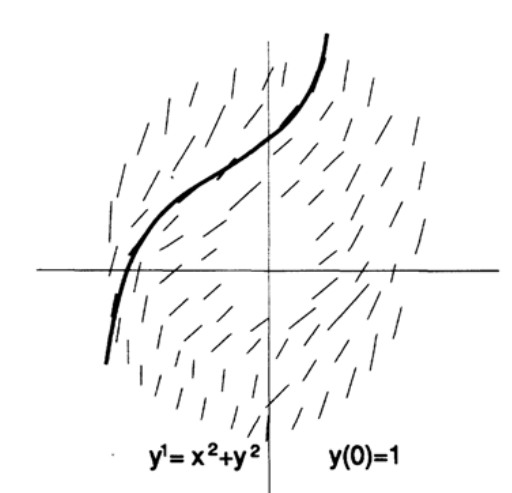
Рисунок 20.II

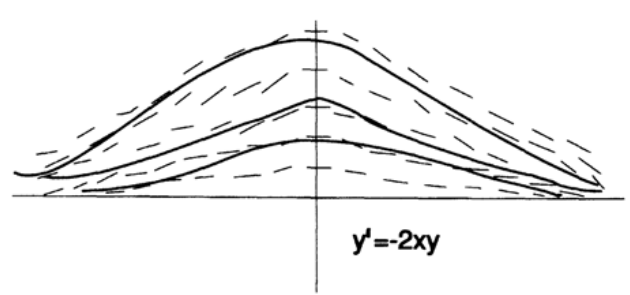
Рисунок 20.III

Эти рассуждения построены для функции

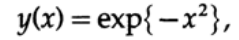
которая является решением дифференциального уравнения

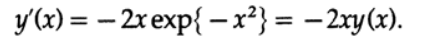
Вероятно, вы уже представили «трубу», которая сначала расширяется, а потом сужается, вокруг «истинного, точного решения» уравнения. Такое представление отлично подходит для случая двух измерений, но когда у меня система из n таких дифференциальных уравнений — 28 в случае задачи о ракете-перехватчике для ВМФ, упомянутой ранее, — тогда эти «трубы» вокруг истинного решения уравнения оказываются не тем, чем кажутся на первый взгляд. Фигура состоящая из четырех кругов в двух измерениях приводит к описанному в 9-ой главе парадоксу n-измерений для десятимерного пространства. Это просто другой взгляд на проблему стабильного и нестабильного моделирования, описанную в предыдущей главе. На этот раз я приведу конкретные примеры связанные с дифференциальными уравнениями.

Как мы численно решаем дифференциальные уравнения? Начиная с обычного дифференциального уравнения первого порядка, мы изображаем поле направлений. Наша задача заключается в том, чтобы имея некоторое заданное начального значение рассчитать значение в следующей ближайшей интересующей нас точке. Если мы возьмем локальный коэффициент наклона прямой, заданный дифференциальным уравнением, и сделаем небольшой шаг вперед по касательной, то мы внесем лишь небольшую ошибку (рисунок 20.IV).

Используя эту новую точку мы переместимся в следующую точку, но как видно на рисунке, мы постепенно отклоняемся от истиной кривой, потому что мы используем коэффициент наклона, предыдущего шага, а не истинный коэффициент наклона для текущего интервала. Чтобы избежать этого эффекта, мы «прогнозируем» некоторое значение, затем используем его, чтобы оценить угловой коэффициент в этой точке (используя дифференциальное уравнение), а затем используем усредненное значение углового коэффициента на двух границах интервала в качестве углового коэффициента для этого интервала.

Затем, используя этот усредненный угловой коэффициент, мы делаем еще один шаг вперед, на этот раз используя формулу «коррекции». Если значения, полученные при помощи формул «прогнозирования» и «коррекции» достаточно близки, значит мы предполагаем, что наши расчёты достаточно точны, иначе мы должны уменьшить размер шага. Если разница между значениями слишком мала, то мы должны увеличить размер шага. Таким образом, традиционная схема «предиктор-корректор» имеет встроенные механизм для проверки ошибки на каждом шаге, но эта ошибка на конкретном шаге ни каким образом и ни в каком смысле не является общей накопленной ошибкой! Абсолютно ясно, что накопленная ошибка зависит от того сходится или расходится поле направлений.

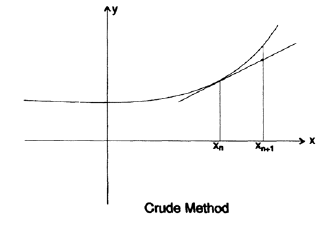
Рисунок 20.IV

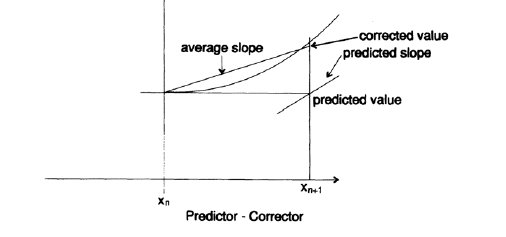
Рисунок 20.V

Мы использовали простые прямые линии как для шага прогноза так и для шага коррекции. Использование полином высших степеней дает более точный результат; обычно используются полиномы четвертной степени (решение дифференциальных уравнений методом Адамса — Башфорта, методом Мильна, методом Хэмминга и т.д. ). Таким образом, мы должны использовать значения функции и ее производных в нескольких предыдущих точках для прогнозирования значения функции в следующей точке, после чего мы используем подстановку этого значения в дифференциальное уравнение и аппроксимируем новое значение углового коэффициента. Используя новое и предшествующие значения углового коэффициента а так же значения искомой функции, мы корректируем полученное значение. Самое время заметить, что корректор это не что иное как цифровой рекурсивный фильтр, в котором входные значения – это производные, а выходные значения – значения искомой функции.

Стабильность и другие понятия, обсуждаемые ранее, остаются актуальными. Как упоминалось ранее, существует дополнительная петля обратной связи для спрогнозированного решения дифференциального уравнения, которое в свою очередь используется в расчёте скорректированного углового коэффициента. Оба этих значения используются в решении дифференциального уравнения, рекурсивные цифровые фильтры – это просто формулы, и ничего более. При этом они не являются передаточными характеристиками, как их принято рассматривать в теории цифровых фильтров. В данном случае просто-напросто происходит вычисление значений дифференциального уравнения. При этом разница между подходами существенна: в цифровых фильтрах происходит линейная обработка сигнала, в то время как при решении дифференциальных уравнений присутствует нелинейность, которая вносится вычислением значений производных функции. Это не то же самое, что цифровой фильтр.

Если вы решаете систему из n дифференциальных уравнений, то вы имеете дело с вектором из n компонент. Вы прогнозируете следующее значение каждого компонента, оцениваете каждую из n производных, корректируете каждое из спрогнозированных значений, после чего принимаете результат вычислений на данном шаге или отклоняете его, если локальная ошибка слишком велика. Вы склонны думать о небольших ошибках как о «трубе», окружающей истинную вычисленную траекторию. И я снова призываю помнить о парадоксе четырех окружностей, в высокоразмерных пространствах. Такие «трубы» могут оказаться не тем, чем они кажутся на первый взгляд.

Теперь позвольте мне отметить значительную разницу между двумя походами: вычислительными методам и теорией цифровых фильтров. В распространенных учебниках описаны только методы вычислительной математики, которые аппроксимируют функции полиномами. Рекурсивные фильтры же используют частоты в формулах оценки! Это приводит к существенным отличиям!

Чтобы увидеть разницу, давайте представим, что мы разрабатываем симулятор посадки человека на Марс. Классический подход концентрируется на форме траектории посадки и использует приближение полиномами для локальных областей. Полученный путь будет иметь точки разрыва в ускорении, так как мы пошагово движемся от интервала к интервалу. В случае частотного подхода, мы сконцетрируемся на получении правильных частот и позволим местоположению быть таким, каким оно получится. В идеальном случае обе траектории будут одинаковыми, на практике же они могут существенно отличаться.

Какой из походов следует использовать? Чем больше вы будете задумываться об этом, тем больше вы будете склоняться к тому, что пилот в тренажере хочет получить «ощущение» поведения посадочного модуля, и похоже, что частотный отклик тренажера должен хорошо «ощущаться» пилотом. Если местоположение будет немного отличаться, то петля обратной связи скомпенсирует это отклонение в процессе посадки, но если если «ощущение» управления будет отличаться во время реального полета, то пилот будет обеспокоен новыми «ощущениями», которых не было в симуляторе. Мне всегда казалось, что симуляторы должны готовить пилотов к реальным ощущениям настолько, насколько это возможно (конечно же мы не можем долго имитировать пониженную гравитацию на Марсе), для того, чтобы они чувствовали себя комфортно, когда в реальности столкнутся с ситуацией, с которой они многократно сталкивались в тренажере. Увы, мы знаем слишком мало о том, что пилот «ощущает». Ощущает ли пилот только действительные частоты из разложения Фурье, или они также ощущают комплексные затухающие частоты Лапласа (или может быть мы должны использовать вейвлеты?). Чувствуют ли разные пилоты одинаковые вещи? Мы должны знать больше, чем мы знаем сейчас, об этих существенных для проектирования условиях.

Описанная выше ситуация – это стандартное противоречие между математическим и инженерным подходом к решению задачи. Эти подходы имеют разные цели при решении дифференциальных уравнений (как и в случае многих других задач), следовательно они приводят к разным результатам. Если вы столкнетесь с моделированием, то вы увидите, что существуют скрытые нюансы, которые оказываются очень важны на практике, но о которых математики ничего не знают и всячески будут отрицать последствия от пренебрежения ими. Давайте взглянем на две траектории (Рисунок 20.IV), которые я грубо прикинул. Верхняя кривая точнее описывает местоположение, но изгибы дают совершенно другое «ощущение» по сравнению с реальным миром, вторая кривая больше ошибается в местоположении, но имеет большую точность с точки зрения «ощущения». Я снова наглядно показал, почему я считаю, что человек с глубоким пониманием предметной области задачи должен так же глубоко разобраться и в математических методах ее решения, а не полагаться на традиционные методы решения.

Сейчас я хочу рассказать еще одну историю о ранних днях тестирования противоракеты системы Nike. В то время проходили полевые испытания в Уайт-Сэндс, которые еще называли «полевые испытания телефона». Это были испытательные запуски, в которых ракета должна была следовать по предопределенной траектории и взрываться в последний момент, чтобы вся энергия взрыва не выходила за пределы определенной территорий и наносила больший урон, что было предпочтительнее, чем более мягкое падение отдельных частей ракеты на землю, которое, предположительно, должно было бы нанести меньше урона. Задачей испытаний было получить реальные измерения подъемной силы и лобового сопротивления как функции высоты полета и скорости, для того чтобы отладить и улучшить конструкцию.

Когда я встретил своего вернувшегося с испытаний друга, он бродил по коридорам Лабораторий Белла и выглядел довольно несчастным. Почему? Потому что первые два из шести запланированных запусков провалились в середине полёта и никто не знал по чему. Данные необходимые для дальнейших этапов проектирования были не доступны, а это означало серьезные проблемы для всего проекта. Я сказал, что если он сможет мне предоставить дифференциальные уравнения, описывающие полёт, то я смогу посадить девочку их решать (получить доступ к большим компьютерам в поздних 1940-ых было непросто). Примерно через неделю они предоставили семь дифференциальных уравнений первого порядка и девочка была готова начать. Но какие были начальные условия за мгновение до начала проблем в полете? (В те дни у нас не было достаточного количества вычислительных мощностей, чтобы быстро просчитать всю траекторию полёта.) Они не знали! Данные телеметрии были непонятны за мгновение до сбоя. Я был не удивлен и это не тревожило меня. Итак, мы использовали предполагаемые значения высоты, скорости полета, угла атаки и т.д. — по одному начальному условию для каждой из переменных, описывающих траекторию полёта. Иными словами, у меня был мусор на входе. Но ранее я понял, что природа полевых испытаний, которые мы моделировали была такой, что небольшие отклонения от предложенной траектории автоматически исправлялись системой наведения! Я имел дело с сильно сходящимся полем направлений.

Мы обнаружили, что ракета была устойчивой по поперечной и вертикальной осям, но при стабилизации одной из них избыток энергии приводил к колебаниям по другой оси. Таким образом имели место не только колебания по поперечной и вертикальным осям, но и периодическая передача возрастающей энергии между ними, вызванная вращением ракеты вокруг продольной оси. Как только были продемонстрированы рассчитанные кривые для небольшого участка траектории, все тут же поняли, что не была учтена перекрестная стабилизация, и все знали как это исправить. Итак, у нас появилось решение, которое так же позволило считать испорченные данные телеметрии, полученные во время испытаний, и уточнить период передачи энергии – по сути дела предоставить правильные дифференциальные уравнения для расчётов. У меня было немного работы, кроме как убедиться, что девушка с настольным калькулятором честно все рассчитала. Итак, мая заслуга заключалась в понимании того, что (1) мы можем смоделировать, что произошло (сейчас это рутина при расследовании аварий, но тогда это было инновация) и (2) поле направлений сходится, поэтому начальные условия могут быть заданы не точно.

Я вам рассказал эту историю для того, чтобы показать, что принцип GIGO работает не всегда. Похожая история произошла со мной во время раннего моделирования бомбы в Лос Аламосе. Постепенно я пришел в пониманию, что наши вычислениями, построенные для уравнения состояния, были основаны на довольно неточных данных. Уравнение состояния связывает давление и плотность вещества ( так же температуру, но я ее опущу в данном примере). Данные из лабораторий высокого давления, приближения полученные из изучения землетрясений, плотности звёздных ядер и асимптотической теории бесконечных давлений были изображены в виде точек на очень большом листе миллиметровки (Рисунок 20.VII). Затем при помощи лекал мы нарисовали кривые, которые соединили рассеянные точки. Потом по этим кривым мы построили таблицы значений функции с точностью до 3 знаков после запятой. Это означает что мы просто предполагали 0 или 5 в 4-ом знаке после запятой. Мы использовали эти данные, чтобы построить таблицы с точностью до 5-ого и 6-ого знаков после запятой. На основе этих таблиц были построены наши дальнейшие вычисления. В то время, как я уже ранее упоминал, я был своего рода калькулятором, и моя работа заключалась в том, чтобы считать и тем самым освободить физиков от этого занятия, чтобы позволить им заниматься своей работой.

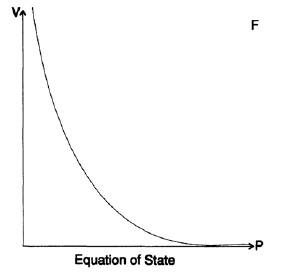
Рисунок 20.VII

После окончания войны, я остался в Лос Аламосе еще на пол года, и одна из причин, почему я это сделал, заключалась в том, что я хотел понять, как настолько неточные данные смогли привести к настолько точному моделированию окончательной конструкции. Я долго размышлял об этом, и я нашел ответ. В середине вычислений мы использовали конечные разности второго порядка. Разность первого порядка показывала значение силы на одной стороне каждой оболочки, а разности примыкающих с двух сторон оболочек давали результирующую силу, сдвигающую оболочку. Мы были вынуждены использовать тонкие оболочки, поэтому мы вычитали очень близкие друг к другу числа, и нужно было использовать много разрядов после запятой. Дальнейшие исследования показали, что когда «штучка» взорвалась, оболочка двигалась вверх по кривой, и, вероятно, иногда частично смещалась назад, поэтому любая локальная ошибка в уравнении состояния была приближена к среднему значению. По настоящему важным было получить кривизну уравнения состояния и, как уже было замечено, она должна была быть в среднем точной. Таким образом, мусор на входе, но точные как никогда результаты на выходе!

Эти три примера показывают то, что неявно упоминалось ранее – если в задаче существует петля обратной связи для используемых переменных, то необязательно знать их значения в точности. На этом базируется замечательная идея Г. С. Блэка о том, как строить петлю обратной связи в усилителях (Рисунок 20.VIII): до тех пор, пока коэффициент усиления очень высокий, только сопротивление одного резистора должно быть точно подобрано, все остальные части могут быть реализованы с низкой точностью. Для схемы, представленной на рисунке 20.VIII мы получаем следующие выражения:

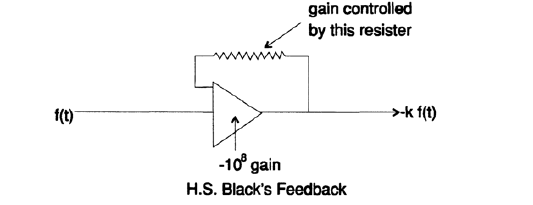
Рисунок 20.VIII

Как видно, практически вся неопределенность измерения сосредоточена в одном резисторе номиналом 1/10, в то время как коэффициент передачи может быть неточным. Таким образом петля обратной связи Блэка позволяет нам строить точные вещи из неточных частей.

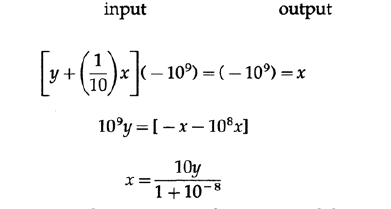
Теперь вы видите, почему я не могу дать вам изящную формулу, подходящую для всех случаев. Она должна зависеть от того, какие вычисления производятся над конкретными величинами. Пройдут ли неточные значения через петлю обратной связи, которая скомпенсирует ошибку, или ошибки выйдут за пределы системы без защиты обратной связью? Если для переменных не предусмотрена обратная связь, то жизненно важно получить их точные значения.
Итак, осознание этого факта способно повлиять на дизайн системы! Хорошо спроектированная система защищает вас от необходимости использования большого количества высокоточных компонентов. Но подобные принципы проектирования все еще неверно понимаются в настоящий момент и требуют тщательного изучения. И дело не в том, что хорошие проектировщики не понимают этого на уровне интуиции, просто не так просто применить эти принципы в методах проектирования, которые вы изучали. Хорошие умы все еще нуждаются во всех тех средствах автоматического проектирования, которые мы разработали. Лучшие же умы смогут встроить эти принципы в изученные методы проектирования, чтобы сделать их доступными «из коробки» для всех остальных.

Обратимся теперь к другому примеру и принципу, который позволил мне получить решение одной важной задачи. Мне было дано дифференциальное уравнение

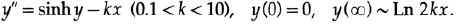
Сразу заметно, что значение условия на бесконечности действительно является правой частью дифференциального уравнения приравненного к нулю, рисунок 20.IX

Но давайте рассмотрим вопрос стабильности. Если значение y в какой-то достаточно удаленной точке x становиться достаточно большим, то значение sinh(y) становиться значительно больше, вторая производная принимает большое положительное значение, а кривая выстреливает по направлению к плюс бесконечности. Аналогично, если значение y слишком мало, то кривая выстреливает по направлению к минус бесконечности. И абсолютно не имеет значения, движемся мы слева направо или справа налево. Раньше, когда я сталкивался с расходящимся полем направлений, я использовал очевидный трюк: интегрировал в противоположном направлении и получал точное решение. Но в данном случае, мы как будто бы находимся на гребне песчаной дюны и как только обе ноги оказываются на одном склоне, мы срываемся вниз.

Рисунок 20.IX

Я пытался использовать разложение в степенные ряды, разложение в нестепенные ряды, приближающие исходную кривую, но проблема никуда не уходила, особенно для больших значений k. Ни я, ни мои друзья не смогли предложить какого-либо адекватного решения. Тогда я отправился к постановщикам задачи и в первую очередь стал оспаривать граничное условие на бесконечности, однако, выяснилось, что это условие связано с расстоянием, измеренным в слоях молекул, а в то время, любой практически реализуемый транзистор имел практически бесконечное количество слоев. Тогда я стал оспаривать уравнение, и они снова выиграли спор, и мне пришлось отступить назад в свой офис и продолжить думать.

Это была важная задача, связанная с проектированием и пониманием транзисторов, которые разрабатывались в то время. Я всегда утверждал, что если задача является важной и корректно поставлена, то я могу найти какое-то решение. Поэтому у меня не было выхода, это было делом чести.

Мне потребовалось несколько дней размышлений, чтобы понять, что нестабильность являлась ключом к подходящему методу. Я строил решение дифференциального уравнения на небольшом интервале при помощи дифференциального анализатора, который у меня был в то время, и если решение выстреливало вверх, то это означало, что я выбрал слишком большое значение углового коэффициента, если же оно выстреливало вниз, значит я выбрал слишком маленькое значение. Таким образом, небольшими шагами, я прошел по гребню дюны, и как только решение срывалось с одной стороны, я знал, что нужно сделать, чтобы вернуться на гребень. Как видите, профессиональная гордость — хороший помощник, когда нужно найти решение важной задачи в сложных условиях. Как же легко можно было отказаться от решения этой задачи, сослаться на то, что она нерешаемая, некорректно поставлена или найти любые другие отговорки, но я по-прежнему верю, что важные и корректно поставленные задачи позволяют получить новую полезную информацию. Ряд задач, связанных с пространственным зарядом, которые я решил при помощи вычислительных методов, имели аналогичную сложность, связанную с нестабильностью в обоих направлениях.

Перед тем как рассказать вам следующую историю, я хочу напомнить вам о тесте Роршаха, который был популярен во времена моей юности. Капля чернил наносится на лист бумаги, после чего он складывается пополам, а когда его снова разворачивают, получают симметричную кляксу достаточно случайной формы. Последовательность этих клякс показывается испытуемым, которых просят рассказать, что они видят. Их ответы используются для анализа «особенностей» их личности. Очевидно, что ответы являются плодом их воображения, поскольку по существу пятно имеет случайную форму. Это как смотреть на облака в небе и обсуждать, на что они похожи. Вы обсуждаете исключительно плоды вашего воображения, а не реальность, и это в какой-то мере открывает новое о вас самих, а не об облаках. Я полагаю, что метод чернильных пятен больше не используется.

А теперь перейдем к самой истории. Однажды, мой друг-психолог из Лабораторий Белла построил машину, в которой было 12 переключателей и две лампочки — красная и зелёная. Вы устанавливали переключатели, нажимали кнопку, и после этого загоралась красная или зелёная лампочка. После того, как первый испытуемый совершал 20 попыток, он предлагал теорию о том, как зажечь зелёную лампочку. Эта теория передавалась следующей жертве, после чего у нее тоже было 20 попыток чтобы предложить свою теорию о том, как зажечь зелёную лампочку. И так до бесконечности. Целью эксперимента ставилось изучение того, как развиваются теории.

Но мой друг, действуя в своем стиле, подключил лампочки к случайному источнику сигналов! Однажды он мне пожаловался, что ни один участник эксперимента (а все они были высококлассными исследователями Лабораторий Белла) не сказал, что не существует закономерности. Я незамедлительно предположил, что ни один из них не был специалистом в области статистики или теории информации — именно эти два типа специалистов не понаслышке знакомы со случайными событиями. Проверка показала, что я был прав!

Это печальное следствие вашего образования. Вы с любовью изучали, как одна теория заменяется другой, но вы не изучали, как отказаться от красивой теории и принять случайность. Именно это и было необходимо: быть готовым признать, что только что прочитанная теория не подходит, а в данных нет какой-либо закономерности, чистая случайность!

Я должен остановиться на это подробнее. Статистики постоянно спрашивают себя: «То что я виду, на самом деле имеет место, или это просто случайный шум?». Они разработали специальные методы тестирования, для ответа на этот вопрос. Их ответы — это не однозначное «да» или «нет», а «да» или «нет» с определенным уровнем уверенности. Порог уверенности в 90% означает, что обычно из 10 попыток вы ошибётесь только один раз, при условии, что все остальные гипотезы корректны. В этом случае одно из двух: или вы нашли то, чего нет (Ошибка первого рода) или вы пропустили то, что искали (Ошибка второго рода). Намного больше данных нужно для того, чтобы получить уровень уверенности в 95%, а в настоящее время сбор данных может быть очень дорогим. Сбор дополнительных данных также требует и дополнительного времени и принятие решения откладывается — это любимая уловка людей, которые не хотят нести ответственности за свои решения. «Нужно больше информации» — скажут они вам.

Я абсолютно серьёзно утверждаю, что большинство производимого моделирования — это не более чем тест Роршаха. Я процитирую выдающегося практика теории управления Джея Форрестера: «Из поведения системы возникнут сомнения, которые потребуют пересмотра исходных предположений. Из процесса переработки исходных предположений о частях и наблюдаемого поведения целого мы улучшаем наше понимание структуры и динамики системы. Эта книга является результатом нескольких циклов повторного изучения, пройденных автором».

Как неспециалисту отличить это от теста Роршаха? Увидел ли он что-то просто потому, что хотел это увидеть или открыл новую грань реальности? К сожалению, очень часто моделирование содержит в себе некоторые корректировки, которые позволяют «видеть только то, что хочется». Это путь наименьшего сопротивления, именно поэтому классическая наука предполагает большое количество предосторожностей, которые в наше время зачастую просто игнорируются.

Вы думаете, что вы достаточно осторожны, чтобы не выдавать желаемое за действительное? Давайте рассмотрим знаменитое двойное слепое исследование, которое является общепринятой практикой в медицине. Сначала доктора обнаружили, что пациенты отмечают улучшение состояния, когда думают, что они получают новое лекарство, в то время как пациенты из контрольной группы, которые знают, что не получаются новое лекарство, не чувствуют улучшения состояния. После этого доктора рандомизировали группы и стали давать некоторым пациентам плацебо, чтобы они не могли ввести в заблуждение докторов. Но к своему ужасу, доктора обнаружили, что врачи, знавшие, кто принимает лекарство, а кто нет, так же обнаруживали улучшения состояния у тех, у кого оно ожидалось и не находили улчшения у тех, у кого оно не ожидалось. В качестве последнего средства доктора стали повсеместно приняли метод двойного слепого исследования — пока все данные не будут собраны, ни доктора, ни пациенты не знают, кто принимает новое лекарство, а кто нет. В конце эксперимента статистики открывают запечатанный конверт и проводят анализ. Доктора, которые стремились к честности, открыли что сами таковыми не являются. Вы проводите моделирование настолько лучше, что вам можно доверять? Вы уверены что вы просто не нашли то, что так стремились найти? Самообман очень распространен.

Я начал 19 главу с того, что задал вопрос, почему все должны верить произвденному моделированию? Сейчас эта проблема стала для вас более очевидной. Не так просто ответить на этот вопрос, пока вы не приняли намного больше мер предосторожности, чем обычно принято. Помните так же, что в вашем высокотехнологичесокм будущем, вероятнее всего, вы будете представлять сторону заказчика моделирования, и на основе его результатов вам придется принимать решения. Не существует других путей, кроме моделирования, что получить ответ на вопрос «Что если … ?». В 18 главе я рассматривал решения, которые должны быть приняты, а не все время откладываться, если организация не собирается бесконечно рыться и дрейфовать — я предполагаю, что вы будете среди тех, кто будет должен принять решение.

Моделирование необходимо для ответа на вопрос «Что если … ?», но при этом оно полно подводных камней, и не следует доверять его результатам просто потому, что были задействованы большие людские и аппаратные ресурсы, чтобы получить красивые цветные распечатки или кривые на осциллографе. Если вы тот, кто принимает окончательное решение, то вся ответственность лежит на вас. Коллегиальные решения, которые приводят к размытию ответственности, редко являются хорошей практикой — как правило они являются посредственным компромиссом, в котором отсутствуют достоинства какого-либо из возможных путей. Опыт научил меня, что решающий босс намного лучше болтающего попусту босса. В этом случае вы точно знаете где вы находитесь и можете продолжить работу, которая должна быть сделана.

Вопрос «Что если … ?» часто будет вставать перед вами в будущем, поэтому вам нужно как следует разобраться с основами и возможностями моделирования, чтобы быть готовыми оспорить результаты и разобраться в деталях, там где это необходимо.

Продолжение следует...

Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)

Автор: Алексей JetHackers Стаценко

Источник