Ричард Хэмминг: Глава 11. Теория кодирования — II

«Цель этого курса — подготовить вас к вашему техническому будущему.»

Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 393k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 25 (из 30) глав. И ведем работу над изданием «в бумаге».

11. Теория кодирования — II

(За перевод спасибо erosinka, которая откликнулась на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

Две вещи должны быть ясны из предыдущей главы. Во-первых, мы хотим, чтобы средняя длина L отправленного сообщения была как можно более маленькой (чтобы сохранить ресурсы). Во-вторых, это должно быть подкреплено статистической теорией, так как мы не можем знать какое сообщение будет отправлено, но мы можем знать некоторые статистистические данные, используя предыдущие сообщения, и последующие выходные данные, возможно, будут похожи на предыдущие. Для самой простой теории, единственной, какую мы можем обсуждать здесь, нам понадобятся вероятности появления в сообщении индивидуальных символов. Вопрос их получения не является частью теории, но они могут быть получены путем исследования прошлого опыта или воображаемым гаданием об использовании в будущем системы, которую Вы проектируете.

Таким образом, мы хотим мгновенно однозначно декодируемый код для данного набора входных символов, si, вместе с их вероятностями, pi. Какую длину li мы должны установить (учитывая что мы должны подчиняться неравенству Крафта), чтобы получить минимальную среднюю длину кода? Хаффман решил эту проблему дизайна кода.

Хаффман первым показал, что следующие неравенства должны быть верны для кода минимальной длины. Если pi расположены в убывающем порядке, то li должны быть в возрастающем порядке.

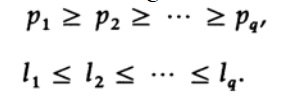
Допустим, pi в указанном порядке, но хотя бы одна пара li — нет. Рассмотрим эффект перестановки символов, связанных с теми двумя, которые не в указанном порядке. Перед перестановкой вклад этих двух членов уравнения в среднюю длину кода L

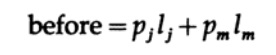
и после перестановки

Все остальные члены в сумме L остаются те же. Разница может быть записана как

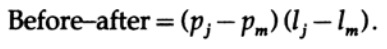
Один из этих членов предполагается отрицательным, следовательно после перестановки двух символов средняя длина кода L уменьшится. Таким образом для минимальной длины кода мы должны иметь два неравенства.

Далее Хаффман обнаружил, что мгновенно дешифруемый код имеет дерево решений, и каждый узел должен иметь два выхода, в противном случае это пустая попытка, следовательно, имеются два символа с наибольшей длинной, которые имеют одинаковую длину.

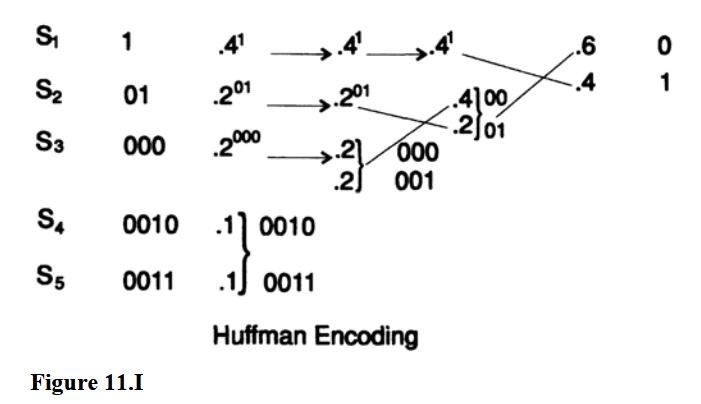
Для иллюстрации кода ХАффмана мы используем классический пример. Пусть p(s1) = 0.4, p(s2) = 0.2, p(s3) = 0.2, p(s4) = 0.1 и p(s5) = 0.1. Это изображено на рисунке 11.I Тогда Хаффман утверждал на основании значений выше, что он мог комбинировать (объединить) два наименее частых символа (которые должны иметь одинаковую длину) в один символ с общей вероятностью с общими битами вплоть до последнего бита, который отбрасывается, таким образом получая код на один символ меньше. (?) Повторяя это снова и снова он приходил к системе с двумя символами, для которых он знал, как приписать представление кода, а именно одному символу — 0, а другому — 1.

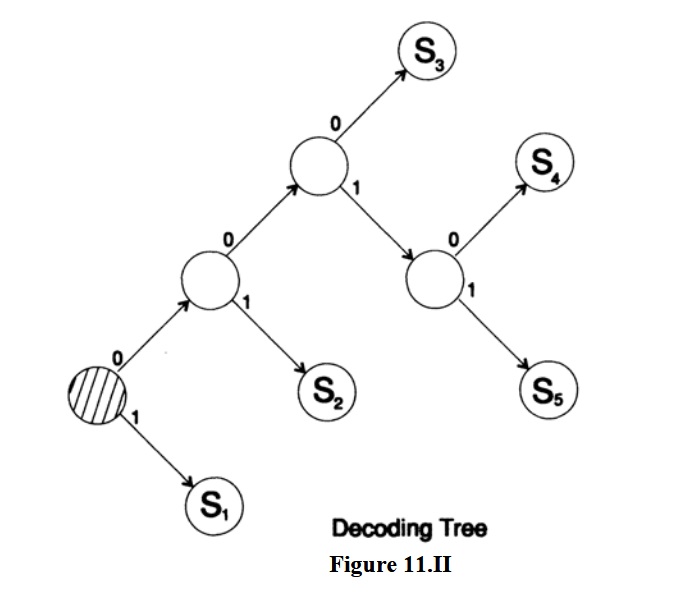
Теперь идя в обратную сторону, нам нужно на каждой стадии разделить символ, который получился из комбинации двух символов, сохраняя те же ведущие биты, но добавляя к одному символу 0, а к другому — 1. Таким методом мы придем к коду минимальной длины L, снова смотрите рисунок 11.I Так как если бы существовал другой код с меньшей длиной L’, то выполняя шаги вперед, которые изменяют среднюю длину кода на заданное число, он бы пришел к двум символам со средней длиной кода меньше, чем 1, что невозможно. Следовательно, код Хаффмана имеет минимальную длину. Смотрите рисунок 11.II с соответствующим декодирующим деревом.

Этот код не уникален. Прежде всего на каждом шаге процесса приписывание 0 и 1 каждому из символов — это произвольный процесс. Во-вторых, если на каком-либо этапе имеется два символа с одинаковыми вероятностями, то не имеет значения, какой из них будет первым. Это может привести в некоторых случаях к появлению очень разных кодов, но они оба будут иметь одинаковую среднюю длину.

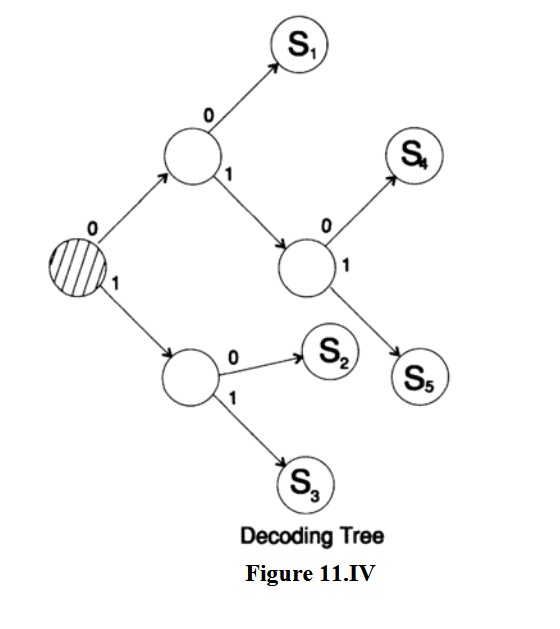
Если поместить комбинированные члены как можно выше, мы получим рисунок 11.III с соответствующим декодирующим деревом на рисунке 11.IV. Средняя длина двух кодов одинакова, но коды и декодирующие деревья отличаются; первое — длинное, а второй — “ветвистое”, и второе менее изменчиво чем первое.

Теперь мы приведем второй пример, чтобы вы были уверены в том, как работает кодирование Хаффмана, так как это естественное желание использовать в процессе разработки кодирующей системы код с как можно более короткой средней длиной. Например, у вас может быть очень много данных предназначенных для хранилища бэкапов, и известно, что ее кодирование с подходящим кодом Хаффмана позволит сэкономить более, чем половину ожидаемого объема хранилища. Пусть p(s1) = ⅓, p(s2) = ⅕, p(s3) = ⅙, p(s4) = 1/10, p(s5) = 1/12, p(s6) 1/20, p(s7) = 1/30, p(s8) = 1/30. Сначала мы проверим, что сумма вероятностей равна 1. Общий знаменатель дробей равен 60. Таким образом мы получаем общую вероятность

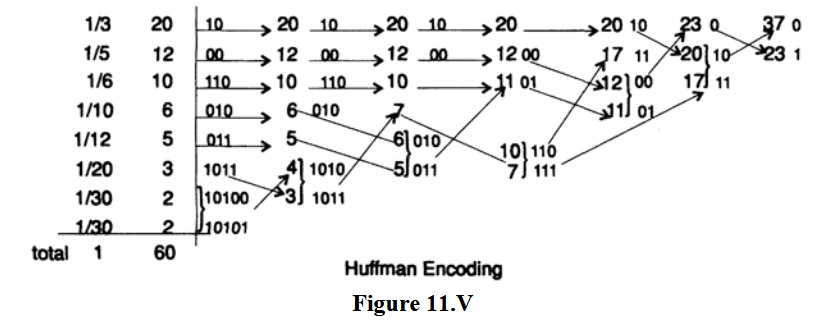
Второй пример проиллюстрирован на рисунке 11.V, где мы опустили 60 в знаменателе вероятностей, так как лишь относительные величины имеют значение. Какова средняя длина кода на символ? Мы вычисляем

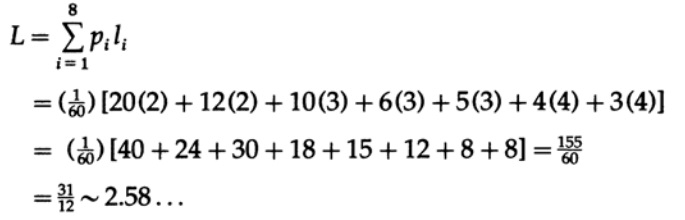
Для блока кода в 8 символов каждый символ будет иметь длину 3 и средняя длина будет равняться 3, что больше, чем 2.58

Заметьте, насколько этот механический процесс подходит для машины. Каждый прямой шаг для кодирования Хаффмана это повторение одного и того же процесса: комбинировать 2 наименьшие вероятности, поместить новую сумму в правильное место в массиве и отметить его. В обратном процессе, мы берем отмеченный символ и разделяем его. Эти программы легко написать для компьютера, таким образом компьютерная программа может вычислить код Хаффмана из данных si и их вероятностей pi. Вспомните, на практике вы хотите приписать символу возврата с очень маленькой вероятностью, так чтобы вы могли завершить декодирующий процесс в конце сообщения. В самом деле, вы можете написать программу, которая сможет отобрать данные для хранения и найти оценку вероятностей (маленькие ошибки приводят только к маленьким изменениям L), найти код Хаффмана, провести кодирование и отправить первый декодирующий алгоритм (дерево) и затем закодированные данные, и все это без человеческого вмешательства! В конце декодирования вы уже получили декодирующее дерево. Таким образом единожды написав программу, вы можете использовать ее в случаях, когда вы посчитаете ее полезной.

Коды Хаффмана были использованы даже в некоторых компьютерах в инструкциях, так как они имели очень маленькую вероятность быть использованными. Следовательно, нам нужно посмотреть на улучшение средней длины кода L, которые мы можем ожидать при использовании кодирования Хаффмана, по сравнению с простых блочным кодированием, которое использует одинаковую длину для всех символов.

Если все вероятности одинаковы и имеется точно 2^k символов, тогда исследование кодирование Хаффмана покажет, что вы получите стандартный блочный код с одинаковой длиной. Если имеется не точно 2^k символов, то некоторые из них будут короче, но трудно сказать, будет ли большинство из них короче на 1 бит, или же некоторые будут короче на 2 и более бит. В любом случае, значение L будет таким же, и не намного короче, чем в соответствующем блочном коде.

С другой стороны, если каждая из pi больше ⅔ (сумма всех последующий вероятностей, кроме последней), тогда вы получите код с запятой, в котором 1 символ имеет длину 1 (0), один символ — 2 (10), и так далее до конца, где у вас будет два символа одинаковой длины (q-1): (1111...10) и (1111...11). В этом случае длина L может быть намного короче, чем у соответствующего блочного кода.

Правило: кодирование Хаффмана окупается, если вероятности символов очень разные, и не окупается, когда они примерно равны.

Когда в процессе ХАффмана появляются две равные вероятности, они могут быть расположены в любом порядке, и таким образом коды могут получиться очень разными, хотя средняя длина кода L в обоих случаях будет одинаковой. Естественно спросить, какой порядок следует выбрать в случае двух равных вероятностей. Разумным критерием является минимизация вариации кода так, что сообщения одинаковой длины в исходных символах имеют примерно одинаковую длину в закодированном виде, вы не хотите, чтобы исходное короткое сообщение было случайно закодировано длинным сообщением. Правило простое: каждую новую вероятность вставлять в таблицу как можно выше. В самом деле, если вы поместите ее выше символа со слегка большей вероятностью, то вы значительно уменьшите вариацию и лишь слегка увеличите L; так что это хорошая стратегия.

Выполнив все шаги мы перейдем к кодированию исходников (хотя мы ни в коем случае не прошли всю тему). Мы обратимся к кодирующему каналу с моделированным шумом. Канал, по предположению, имеет шум, что означает, что некоторые биты были изменены в процессе передачи (или хранения). Что можно сделать?

Обнаружение единственной ошибки довольно просто. К блоку из (n-1) битов нужно прикрепить n-ный бит с таким значением, что все n битов имеют четное количество 1 (или нечетное, если хотите, но мы будем использовать четное число). Это называется проверкой на четность (нечетность).

Таким образом, если все отправленные сообщения будут обладать этим свойством, то на принимающем конце можно проверить, выполнено ли оно. Если проверка на четность не пройдена, будет известно, что есть как минимум одна ошибка, в действительности, нечетное количество ошибок. Так как является благоразумным использовать системы с низкой вероятностью ошибки в любой позиции, то вероятность нескольких ошибок должна быть ещё ниже.

Для математической пригодности мы делаем предположение, что канал имеет белый шум, что означает 1) каждая позиция в блоке из n бит имеет одинаковую вероятность ошибки с любой другой позицией и 2) ошибки в различных позициях некоррелированы, что означает независимы. С этими предположениями, вероятности ошибок равны

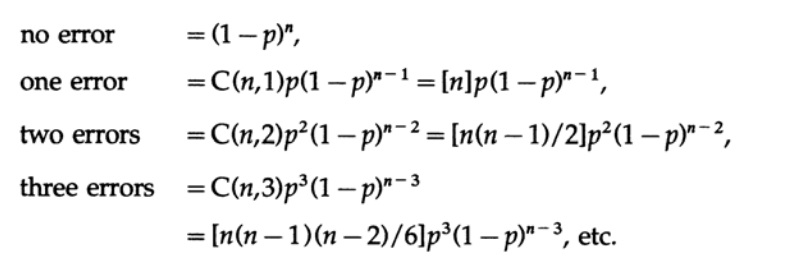
Из этого следует, что, если, как обычно, p мало относительно длины блока n (что означает, произведение np мало), то множественные ошибки гораздо менее вероятны, чем единственные ошибки. Выбор длины n для данной вероятности p является инженерным решением. Если n мало, то у вас будет бОльшая избыточность (отношение количества отправленных битов к минимально возможному количеству битов n/(n-1)), чем с бОльшим n, но если np велико, то у вас будет малая избыточность, но более высокая вероятность не обнаружить ошибку. Вы должны принять инженерное решение о том, как сбалансировать эти два эффекта.
При обнаружении единственной ошибки можно попросить переслать сообщение заново, ожидая корректного результата во второй раз, или в третий и так далее. Однако, если хранимое сообщение некорректно, то вы будете просить о повторной передаче до тех пор, пока не появится другая ошибка, и возможно, у вас будет две необнаруженные ошибки в схеме обнаружения одиночных ошибок. Таким образом, повторные передачи должны зависеть от ожидаемой природы ошибок.

Такие коды широко использовались даже во времена реле. Телефонная компания использовала в центральных офисах и в ранних релейных машинах код 2-из-5, что означало, что только 2 из 5 реле были в положении “включено”. Такой код использовался для представления десятичной цифры, так как C(5, 2)=10. Если не точно 2 реле были в положении “включено”, это означало ошибку, и был повтор. Так же существовал код 3-из-7, очевидно, код с проверкой нечетности.

Я впервые познакомился с этими кодами 2-из-5 в процессе использования релейного компьютера Модель 5 в Белл Лабс, и я был впечатлен не только их помощью в получении правильного ответа, но, что более важно по моему мнению, они давали техническому персоналу возможность в действительности обслуживать машины. Любая ошибка обнаруживалась машиной практически в момент совершения, и следовательно указывала техническому персоналу правильное направление, вместо того чтобы водить их за нос, заставляя менять настройки корректно работающих частей в попытках найти неисправность.
Нарушая временную последовательности повествования, но оставаясь в идейной, AT&T (прим. американский транснациональный телекоммуникационный конгломерат) однажды спросил меня, как использовать кодирование, если люди использовали алфавит из 26 букв, 10 десятичных цифр и пробел. Это типично для именования инвентаря, именования частей и многих других наименований вещей, включая именование зданий. Я знал из данных по ошибкам набора телефонных номеров и из долгого опыта в программировании, что у людей есть сильно выраженная склонность к переставлению смежных цифр: 67 может стать 76, а так же к замене изолированных цифр (обычно удваивая цифру: 556 вероятно станет 566). Таким образом, обнаружение однократных ошибок недостаточно. Я привел двоих очень способных людей в переговорную комнату и задал им вопрос. Я отвергал предложение за предложением как недостаточно хорошие, пока наконец один из них, Эд Гильберт, не предложил взвешенный код. В частности, он предложил обозначить числами 0, 1, 2, … 36 символы 0, 1, … 9, A, B, …, Z, пробел. Затем он вычислял не сумму значений, а имел ли к-тый символ значение (отмеченное для удобства) Sk, тогда для сообщения из n символов мы вычисляем

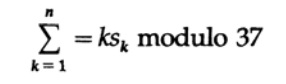
“По модулю” здесь означает, что взвешенная сумма делится на 37 и только остаток от деления используется. Чтобы закодировать сообщение из n символов, оставьте первый символ, k=1, пустым и независимо от значения остатка, которое меньше 37, вычьте его из 37 и используйте соответствующий символ для проверки, который нужно поставить на первую позицию. Таким образом, все сообщение с проверяющим символом на первой позиции будет иметь проверочную сумму равную 0. Если вы рассмотрите перестановку любых двух различных символов или замену единственного символа, вы заметите, что это сломает взвешенную проверку четности, по модулю 37 (при условии, что заменённые символы находятся на расстоянии не равном 37 символов). Не вникая в детали, отметим, что важно, чтобы модуль был простым числом, каким 37 и является.

Чтобы получить взвешенную сумму символом (фактически, их значения), при желании вы можете избегать произведений и использовать только сложения и вычитания. Расположите символы по порядку в столбце и вычислите промежуточные суммы, затем промежуточные суммы промежуточных сумм по модулю 37, затем дополните это по отношению к 37, и вы получите контрольный символ. Как иллюстрация с использованием w, x, y, z.

На принимающей стороне вы повторно вычитаете модуль до тех пор, пока не получите или a-0 (корректный символ) или a — отрицательное число (неправильный символ).

Если вам необходимо использовать это кодирование, например, для наименования инвентаря, то если неправильное название появилось впервые во время передачи, если не раньше (возможно, в предварительном процессе), то ошибка будет обнаружена, вам не придётся ждать до тех пор, пока заказ не будет доставлен до штаб-квартиры, чтобы позднее получить ответ, что не существует такого наименования, или получить неправильный заказ. Ошибка будет обнаружена до того, как заказ покинет вас и следовательно, её легко исправить. Просто? Да! Эффективно против ошибок человека (в отличие от примера с белым шумом), да!

Действительно, в наши дни вы можете увидеть подобный код на книгах с ISBN номером. Это тот же код, только в нем используется 10 десятичных цифр, и число 10 не является простым числом, поэтому им пришлось ввести 11-й символ X, который может появляться временами во время проверки на четность — действительно, примерно каждая 11-я книга будет иметь X как последний символ в номере ISBN для проверки на четность. Тире в основном выполняют декоративную функцию и не используются в кодировании. Проверьте это сами на ваших учебниках. Многие другие крупные организации могли бы использовать такие коды для хорошего эффекта, если бы они хотели приложить усилия.

Я многократно указывал, что я верю, что в будущем информация в форме символов будет важна, и материальные вещи будут менее важны, и следовательно, теория кодирования (представления) информации в удобные коды — это нетривиальная тема. Материал выше дает простой код с обнаружением ошибок для машин, и взвешенный код для использования человеком. Это всего лишь 2 примера, как теория кодирования может помочь в ситуациях, где возможна машинная и человеческая ошибка.

Когда вы думаете об интерфейсе человек-компьютер, одна из вещей, которая вам может пригодиться, это необходимость сделать как можно меньше нажатий клавиш человеком — кодирование ХАффмана под прикрытием! Очевидно, при данных вероятностях различных ветвлений в программных меню вы можете при желании придумать способ уменьшить суммарное количество нажатий клавиш. Таким образом один и тот же набор меню может быть настроен под привычки различных людей, вместо того, чтобы предлагать всем одинаковый интерфейс. В более широком смысле “автоматизированное программирование” в языках высокого уровня является попыткой достичь чего-то наподобие кодирования Хаффмана, чтобы для решения желаемых задач использовать сравнительно небольшое количество нажатий клавиш, а для остальных задач использовать другие клавиши.

Продолжение следует...

Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)

Автор: Алексей JetHackers Стаценко

Источник