Ричард Хэмминг: Глава 17. Цифровые фильтры — IV

«Цель этого курса — подготовить вас к вашему техническому будущему.»

Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 393k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 24 (из 30) главы. И ведем работу над изданием «в бумаге».

Глава 17. Цифровые фильтры — IV

(За перевод спасибо Пахомову Андрею, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

А сейчас мы обратимся к рекурсивным фильтрам, которые имеют следующий вид:

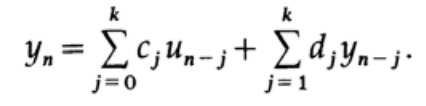
Из этой формулы видно, что мы располагаем значениями только с одной стороны от текущего n-ого значения. Мы используем предыдущие значения сигнала и его значение в текущий момент времени un а так же предыдущие значения полученные на выходе фильтра.
Этот классический подход является результатом того, что часто мы обрабатывает сигнал в режиме реального времени и у нас нет доступа к будущим значениям сигнала.

Вспомнив основы, мы увидим, что если бы у нас были «будущие значения», вероятно, двухстороннее прогнозирование было бы намного более точное. Тогда бы для вычисления yn мы столкнулись бы с системой, которая должна была бы моментально решать линейные уравнения — ничего страшного в век дешевых вычислений. Мы оставим в стороне это наблюдение, в наши дни мы часто записываем сигнал на ленту или другой носитель, и позже обрабатываем данные в лаборатории — и поэтому мы располагаем будущими значениями для какого-то момента времени. Например использовать в обработке изображений рекурсивный цифровой фильтр было бы глупостью, потому что он не использует часть доступной, релевантной информации.

Следующий аспект, на который нужно обратить внимание при использовании предыдущего выходного значения в качестве следующего входного, заключается в наличии обратной связи — а это автоматически поднимает вопрос стабильности. Это условие, за которым мы должны постоянно следить в процессе проектирования рекурсивных фильтров. Это ограничивает то, что мы можем делать. В данном случае стабильность означает, что эффект от начальных условий не начнет преобладать в конечном результате.

Работая с линейной системой, мы видели, что какую бы частоту мы не подали на вход фильтра, когда он в стационарном состоянии, то только эта частота возникает на выходе фильтра, хотя фаза выходного сигнала может быть смещена относительно фазы исходного сигнала. Однако, в переходном состоянии, могут появляться и другие частоты, которые возникают из решения однородного дифференциального уравнения. Рекурсивный фильтр — это не что иное как решение дифференциального уравнения с постоянным коэффициентам при un членах, образующих функцию подкрепления (forcing function).

Следовательно, для стационарного состояния (игнорируя переходные процессы) мы принимаем, что

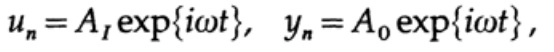
(где A могут быть комплексным числами, чтобы учесть смещение фазы), и это приводит к решению отношения A0/A1 для нахождения передаточной функции:

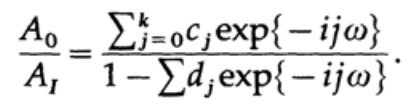
Это выражение является рациональной функцией от комплексной переменной exp{iωt} = z, в отличие от рассмотренного ранее не рекурсивного фильтра, где передаточная характеристика являлась полиномом от z. Разработана теоретическая часть представления функции в виде разложения в ряд Фурье; но пока что еще нет теории по представлению функции как отношения двух рядов Фурье (думаю что нет причин, по которым такой теории может не быть). Поэтому в настоящий момент методы проектирования не являются систематическими (что Кайзер сделал для проектирования не рекурсивных фильтров), а скорее представляют из себя набор трюков.

Таким образом у нас есть фильтр Баттерворта, два типа фильтров Чебышёва (в зависимости от наличия одинаковых пульсаций в полосах пропускания и подавления) и эллиптический фильтр (который так назван из-за использования эллиптических функций), который имеет одинаковые пульсации в обоих полосах.

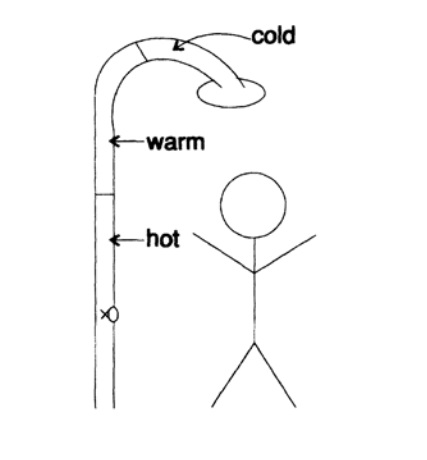
Рисунок 17.1

Я затрону только тему обратной связи. Чтобы сделать проблему обратной связи наглядной, я расскажу вам одну историю обо мне. Однажды давным-давно, я принимал участие в серии из шести получасовых передач на телевидении, посвященных компьютерам и вычислениям. Съемки проходили в основном в Сан-Франциско. Я часто там находился и имел привычку останавливаться в одной и той же комнате в одном и том же отеле — это здорово знать номер во всех деталях, когда уже глубокая ночь и ты уставший или когда тебе приходится вставать посреди ночи — отсюда желание останавливаться в том же номере.

Здорово, что водопроводчик подключил душ к трубам большого диаметра (Рисунок 17.I). В результате, по утрам когда я начинал принимать душ вода была слишком холодной, я больше поворачивал ручку крана с теплой водой, все еще слишком холодно, и больше, по-прежнему слишком холодно, и еще больше, и наконец, когда вода становилась нужной температуры я останавливался. Конечно, вода становилась все горячее и горячее по мере того, как ранее попавшая в трубы вода выходила наружу, и мне приходилось выпрыгивать из душа и пробовать снова найти подходящее положение ручки крана горячей воды. Задержка в подаче горячей воды причиняла мне неудобства. Я оказался, не смотря на богатый опыт, в классической ситуации неустойчивости. Вы можете смотреть на эту ситуацию с одной из двух сторон: или мой отклик был слишком сильный (Я был очень груб в своих действиях) или обнаружение сигнала было слишком запаздывающим (Я был слишком торопливым в регулировке крана). Тот же самый долгоиграющий эффект! Мне никогда раньше не приходилось сталкиваться с большими задержками, поэтому каждый день мое утро начиналось с неудобства! В этом наглядном примере вы можете рассмотреть саму суть неустойчивости.

Здесь я не буду углубляться в дизайн рекурсивных фильтров, только замечу, что во время борьбы с корректирующими формулами для численного решения обыкновенных дифференциальных уравнений я самостоятельно разработал одну теорию.

Корректор в методе предиктор-корректоров имеет форму

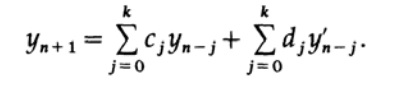
Мы видим, что теперь коэффициенты uj рекурсивного фильтра — это производные yn' выхода фильтра, которые берутся из дифференциального уравнения. В обычных нерекурсивных фильтрах нет петли обратной связи — вычисленные значения yn не появляются позже в правой части выражения. В дифференциальных уравнениях они появляются как и в петле обратной связи так и во входящих в него производных, формируя тем самым еще одну петлю обратной связи, обычно нелинейную. Следовательно, стабильность в области решения дифференциальных уравнений — это более сложная тема, чем в области рекурсивных фильтров.

Такие рекурсивные фильтры часто называются «фильтры с бесконечной импульскной характеристикой» (БИХ — фильтры), потому что единичной возмущение будет отдаваться эхом по петле обратной связи, которое будет затухать в геометрической прогрессии, и то, только в том случае если фильтр стабилен. Я не был бы самим собой, если бы я не задался вопросом, все ли рекурсивные фильтры должны обладать таким свойством. Вскоре я нашел противоположный пример. По правде говоря, это не тот вид фильтров, которые вы обычно будете проектировать, но этот пример показывает, что это утверждение является поверхностным. Если вы спросите себя, все ли, что вы говорите является истинным, то вы будете удивлены, сколько всего окажется ложным, даже в хорошо разработанных областях!

В Главе 26 я затрону проблему работы с экспертами. Сейчас вы увидите пример того, что случается слишком часто. Экспертам что-то рассказали в учебной аудитории, когда они были еще студентами, и они не задавались вопросами, они просто приняли это как факт. И этот принятый факт они постоянно воспроизводят даже не пытаясь проверить, является ли он истинным или нет, особенно применительно к той проблеме, которую они пытаются решить в этот момент.

Позвольте мне сейчас рассказать вам еще одну историю. Одна дама из математического департамента Лабораторий Белла танцевала сквэр-данс с одним из физиков на вечеринке в выходные, а в понедельник с утра, в коридоре она упомянула при мне о проблеме, с которой он столкнулся. Он измерял количество импульсов в радиоактивном эксперименте на каждом из, насколько я помню, 256 энергетических уровней. Это называется «спектр процесса». Его проблема заключалась в получении производной от полученных данных.

Итак, вы знаете, что (a) количество импульсов определенного уровня энергии будет образовывать кривую с разрывами и (b) ее дифференцирование для получения локального углового коэффициента само себе является не простой задачей. Чем больше я думал о её случайной заметке, тем больше я чувствовал, что ему нужен хороший помощник — то есть я! Я отыскал его в телефонном справочнике Лабораторий Белла и объяснил ему свой интерес и как я на него вышел. Он тут же захотел прийти ко мне в кабинет, но я был упрямым, и настаивал на встрече в его лаборатории. Он пробовал предложить свой кабинет, но я все настаивал на его лаборатории. Зачем? Для того, чтобы оценить его способности и решить, стоит ли его проблема моего времени и усилий, так как она обещала быть крепким орешком. Он с блеском прошел тест лабораторией — стало ясно, что он был очень компетентным экспериментатором.

Он был практически на пределе того, что он мог сделать — данные собирались в течении недели, а источник радиации был скрыт множеством экранов. Было не похоже, что можно было сделать что-то еще, чтобы собрать более точные данные. Более того, вскоре я убедился, несмотря на то, что я знал мало подробностей, что его эксперимент важен для физики так же как и для Лабораторий Белла. Итак, я взялся за эту задачу. Мораль: в какой-то мере вы можете выбирать, и работать над теми задачами, которые, как вы считаете, являются важными.

Очевидно, что это была проблема сглаживания, а Кайзер, фактически, только что обучил меня самого, поэтому что могло быть лучше, чем привести экспериментатора к Кайзеру и попросить Кайзера спроектировать подходящий дифференцирующий фильтр? Сразу же начались проблемы. Кайзер всегда думал о сигнале как о функции времени, а о площади под кривой как об энергии, а в этом случае энергия была независимой переменной! В этом месте проблема с Кайзером повторялась до тех пор, пока я прямо не сказал ему: «Хорошо, его энергия это время, а измерения, импульсы, это напряжение». Только после этого Кайзер смог решить задачу.

Проклятье экспертов заключается их ограниченном понимании того, что они могут сделать. Я упоминал вам что Кайзер очень способный человек, но его опыт, как это часто случается с экспертами, ограничил его виденье. Сможете ли вы в свою очередь сделать лучше? Я надеюсь подобные истории помогут вам избежать этой ловушки.

Как я ранее замечал, обычно спектр полезного сигнала находится в нижней части полосы Найквиста, а спектр шума распределен по всей полосе Найквиста, таким образом нам нужно было отыскать частоту среза между полезным сигналом физика и плоским белым шумом. Как же ее найти? Сначала я выпытал у физика теоретическую модель эксперимента, которая была у него в голове — это было множество узких спектральных линий в форме гауссовых функций поверх широкой гауссовой функции (я сомневался в том, что это распределение Коши, но не спорил с ним, так как разница была бы очень маленькой, учитывая природу данных, которые у нас были). Итак, мы смоделировали это распределение, и он подготовил некоторое количество синтетических данных соответствующих этой модели. Быстрый спектральный анализ сигнала через быстрое преобразование Фурье, показал что сигнал заключен в нижней 1/20 части полосы Найквиста. Далее, мы обработали таким же образом его экспериментальные данные и получили то же самое местоположение частоты среза! Какая удача! (Возможно, удача должна быть приписана мастерству экспериментатора). Однажды, теория и практика сошлись! Оказалось, что мы были способны отфильтровать 95% шума. Наконец, Кайзер написал для него программа, которая синтезировала фильтр для заданой частоты среза, которую задавал экспериментатор.

Программа (1) рассчитала подходящий дифференцирующий фильтр, (2) написала программу для расчета сглаженного выхода и после этого (3) обработала данные этим фильтром без каких-либо вмешательств со стороны физика.

Позже я поймал физика за регулировкой частоты среза для разных частей данных об энергетических уровнях, полученных за одну серию измерений и был вынужден напомнить ему, что существуют определенные «степени свободы» и то, что он делает не является честной обработкой данных. Намного более проблематичным стало, когда дела шли хорошо, уговорить его выжать максимум из его данных (получение которых было очень дорогим) — ему следовало работать с квадратными корнями из его импульсов, так как они имели одинаковую дисперсию. Наконец, он это понял и поступил таким образом. Он и Кайзер написали классическую работу в этой области, которая открыла дверь к новым вещам, которые можно было бы сделать.

Мой вклад? Главным образом, вначале определить проблему, потом свести правильных людей вместе, потом наблюдать за Кайзером чтобы поставить его перед фактом того, что фильтрация необходима не только для сигналов как функций времени, и наконец напомнить им то, что они знали из статистики (или должны были бы знать, но, возможно, и не знали).

На основе моего, мне кажется, что необходимость такой роли возрастает по мере того, как люди становятся все более глубокими специалистами во все более узких областях знаний. Кому-то нужно сохранять широкий кругозор и следить за тем, чтобы вещи делались честно. Я думаю я пришел к этой роли после очень долго образования под началом Джона Тьюки в дополнение к хорошему фундаменту в форме универсального инструмента Науки, именуемого Математикой. Я буду говорить о природе Математике в Главе 23.

Большая часть обработки сигналов приходится на сигналы во времени. В то же время большинство цифровых фильтров спроектирована для маленьких, узкоспециализированных исследований, которые вовсе необязательно связаны с сигналами во времени. Здесь я попрошу Вас быть внимательным в будущем. Предположим, вы руководите делами на самом верху, и вам интересны данные, которые показывают более ранние затраты на рабочую силы по отношению к оборудованию. Это будут зашумленные данные, но вам все же хочется понимать, в обычном смысле, что же происходит в организации — какие долгосрочные процессы происходят — те, которые настолько медленные, что люди будут осмысливать их, когда они уже произойдут, но тем не менее понимать и улавливать которые фундаментально важно, если вы хотите быть хорошим управляющим. Вам понадобится цифровой фильтр, чтобы сгладить данные и увидеть намеки на тренд, если он существует. Вы не хотите найти тренд, которого не существует, но если он существует, то вам очень хочется знать, каким он был ранее чтобы прогнозировать то, каким он скорее всего будет в ближайшем будущем. На самом деле, вам захочется увидеть изменения в наклоне тренда, если данные позволяют это увидеть. Некоторые сигналы, такие как огневая мощь по отношению к водоизмещению корабля, не привязаны ко времени, но при этом могут многое вам рассказать о текущем состоянии флота. Конечно же, вы можете изучить это отношение и как функцию времени.

На вершине вашей карьере вы будете способны использовать множество низкоуровневых цифровых фильтров для сигналов как функции времени и не только, чтобы лучше управлять делами. Поэтому, я утверждаю, что вы вероятно синтезируете намного больше цифровых фильтров для таких нестандартных вещей, чем для понижения размерности данных радара и подобных классических применений. Обычно именно в новых применениях знания можно получить наибольшую отдачу.

Позвольте мне высказать некоторые опасения относительно некорректного применения интеллектуальных инструментов, более подробно я буду говорить о темах, близких к статистике, в Главе 27. Анализ посредством разложения в ряд Фурье предполагает линейность лежащей в основе модели. Вы можете использовать его для немного нелинейных случаев, но все же чаще искусно сделанный анализ разложением в ряды Фурье проваливает, так как исследуемое явление слишком нелинейно по своей природе. Я видел как миллионы долларов были потрачены впустую, когда было довольно очевидно для аутсайдеров, что нелинейности исказят весь линейный анализ, сделанный приближением рядами Фурье. Когда им указали на это, их ответ был, что они не знали каким еще подходом можно было воспользоваться, поэтому они продолжали делать неправильные вещи! И я здесь не преувеличиваю.

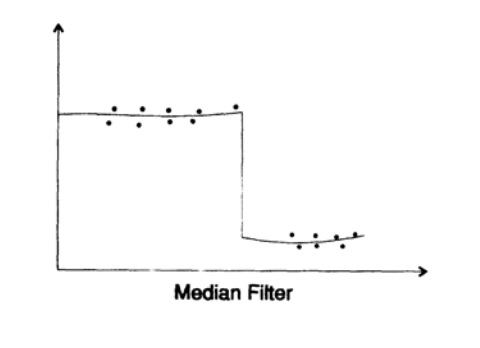
Рисунок 17.2

Что насчёт нелинейных фильтров? Возможности здесь безграничны и зависят, конечно же, от проблемы с которой вы имеет дело. Я займусь здесь только одним из них, медианным фильтром. Вы считаете выход медианного фильтра для определенного набора данных. Рассмотрим как он работает на практике. Первым делом заметим, что он стремится сгладить любой локальный шум, но как поведет себя фильтр в точке разрыва (рис. 17.2)?

С нечётным количеством членов в медианном фильтре, вы увидите, что выход фильтра остается на верхнем уровне до тех пор, пока больше чем половина точек на входе фильтра не окажется на нижнем уровне, после чего выход фильтра «прыгнет» вниз. Он будет достаточно хорошо следовать за разрывами и не будет пробовать их полностью сгладить! В некоторых случаях это именно тот тип фильтр, который вам подойдёт — локальный шум сглаживается, при этом внезапные изменения в состоянии изучаемой системы не будут потеряны.

Я повторюсь, что анализ посредством рядов Фурье является линейным, в то же время существует большое количество нелинейных фильтров, но теория недостаточно хорошо разработана для чего-то, кроме медианного фильтра. Фильтр Калмана — это еще один пример использования частично нелинейного фильтра, нелинейная часть заключается в самостоятельной «подстройке» фильтра под сигнал.

Напоследок, вот еще одно фундаментальное наблюдение, которое я сделал изучая цифровые фильтры. Однажды изучая книгу посвященную интегралам Фурье, я нашел теорему, которая утверждала что вариация функции умноженная на вариацию ее преобразования должна быть больше чем определенная константа. Я спросил у себя: «Что это такое как не знаменитый принцип неопределенности Квантовой Механики»? Да, каждая линейная теория должна иметь принцип неопределенности связывающий сопряженные переменные. Как только вы приминяете линейный подход, а КМ утверждает абсолютную аддитивность собственных состояний, то вы должны обнаружить принцип неопределенности. Линейная инвариантность времени автоматически приводит к собственным функциям e^iω(t). Они немедленно приводят к рядам Фурье, а они в свою очередь имеют принцип неопределенности. Это как если бы вы надели синие тонированные очки. На что бы вы не посмотрели, оно должно иметь синеватый оттенок!

Поэтому вы на самом деле не уверены, существует ли знаменитый принцип неопределенности КМ или нет; может быть это всего лишь эффект подразумеваемой линейности системы.

Немногие люди хотят верить в то, что то что мы видим зависит от того, с какой стороны мы подходим к проблеме! Очень часто мы видим то, что мы хотим увидеть, и именно поэтому вам следует повсеместно применять научных подход, сомневаясь в собственных убеждения.
Чтобы наглядно это продемонстрировать, я повторю историю Эддингтона о рыбаках. Они ловили рыбу сетью, и когда они исследовали размер пойманных сетью рыб, они решили что существует минимальный размер рыбы в море.

В завершение, если вы не будете сомневаться в принятых правилах, сейчас и потом, то скорее всего вы не станете лидеров в какой бы то ни было области, с другой стороны, если вы будете сомневаться во всем, то вы окажетесь парализованным и ничего не сделает. Когда сомневаться, когда изучать самые основы, когда размышлять самостоятельно, а когда просто идти дальше и принимать вещи как они есть — это вопрос стиля мышления, и я не могу дать простой формулы для решения этой задачи. Вы должны научиться на собственном опыте. Большие достижения обычно приходят вслед за существенными изменениями в основных предположения, на которых основывается область. Состояние нашего знания определяет баланс между различными аспектами проведения исследования. Похоже, что когда вы молоды интуиция и прозорливость имеют больше времени чтобы окупиться, но когда вы стары, на это остается меньше времени и вероятно следует сконцентрироваться на том, что у вас уже под рукой.

Продолжение следует...

Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)

Автор: MagisterLudi

Источник