Доброго времени суток!
Вы всегда хотели знать о принципах шифрования с открытым ключом, но боялись спросить? Нет? Все равно статья интересная (и даже понятная), а в конце лежит игрушка по мотивам исследовавшегося материала.
Итак, тема — шифрование с открытым ключом, а точнее, White-Box Encrypting. Разница в том, что у «коробки» вместо обычной шифровальной функции некая программа, в которой эта функция и спрятана. Но об этом я расскажу позже, а сначала…

Описание
Что такое шифрование, я полагаю, многим понятно хотя бы интуитивно, но что такое открытый ключ и зачем он нужен? Где это используется? Насколько его криптостойкость хороша?
Рассмотрим такую задачу:
Дано:
- Секретное сообщение;
- Человек #1, назовем его Алёной;
- Человек #2 — Лёша;
- Незащищенный канал связи.
Задача:
Алёне нужно отправить секретное сообщение с техзаданием Лёше по этому каналу.
Решение:
Лёша не может работать без четкого техзадания, поэтому он пишет алгоритм шифрования с открытым ключом, состоящий из двух элементов – сам алгоритм шифрования (открытый) и алгоритм расшифровки (закрытый). Первый алгоритм он отправляет Алёне, а второй оставляет себе – на то он и закрытый.

Алёна радостно получает алгоритм, применяет к сообщению, получает зашифрованные данные, которые она и отправляет нашему герою. Тот, в свою очередь, применяет к этим данным свой алгоритм расшифровки, получая исходное секретное сообщение. Все довольны — проект выполнится в срок.

Пусть все не так радужно — злоумышленник перехватил передачи. Это беда — имея алгоритм шифрования и зашифрованные данные, злодей сможет восстановить секретное сообщение, особенно, если функция шифрования задана явно.
Решением стало white-box шифрование – вместо открытого ключа Лёша отправляет Алёне программу, в которой этот алгоритм спрятан (обфусцирован, усложнен), так что у злоумышленника подобрать эту функцию вряд ли получится. Гораздо быстрее найти исходное сообщение полным перебором (brute force), а это задача класса NP, так что чем больше сообщение и сложнее алгоритм, тем больше времени он на это потратит.
| Кол-во знаков | Кол-во вариантов | Стойкость | Время перебора |
|---|---|---|---|
| 1 | 36 | 5 бит | менее секунды |
| 2 | 1296 | 10 бит | менее секунды |
| 3 | 46 656 | 15 бит | менее секунды |
| 4 | 1 679 616 | 21 бит | 17 секунд |
| 5 | 60 466 176 | 26 бит | 10 минут |
| 6 | 2 176 782 336 | 31 бит | 6 часов |
| 7 | 78 364 164 096 | 36 бит | 9 дней |
| 8 | 2,821 109 9x1012 | 41 бит | 11 месяцев |
| 9 | 1,015 599 5x1014 | 46 бит | 32 года |
| 10 | 3,656 158 4x1015 | 52 бита | 1 162 года |
| 11 | 1,316 217 0x1017 | 58 бит | 41 823 года |
| 12 | 4,738 381 3x1018 | 62 бита | 1 505 615 лет |
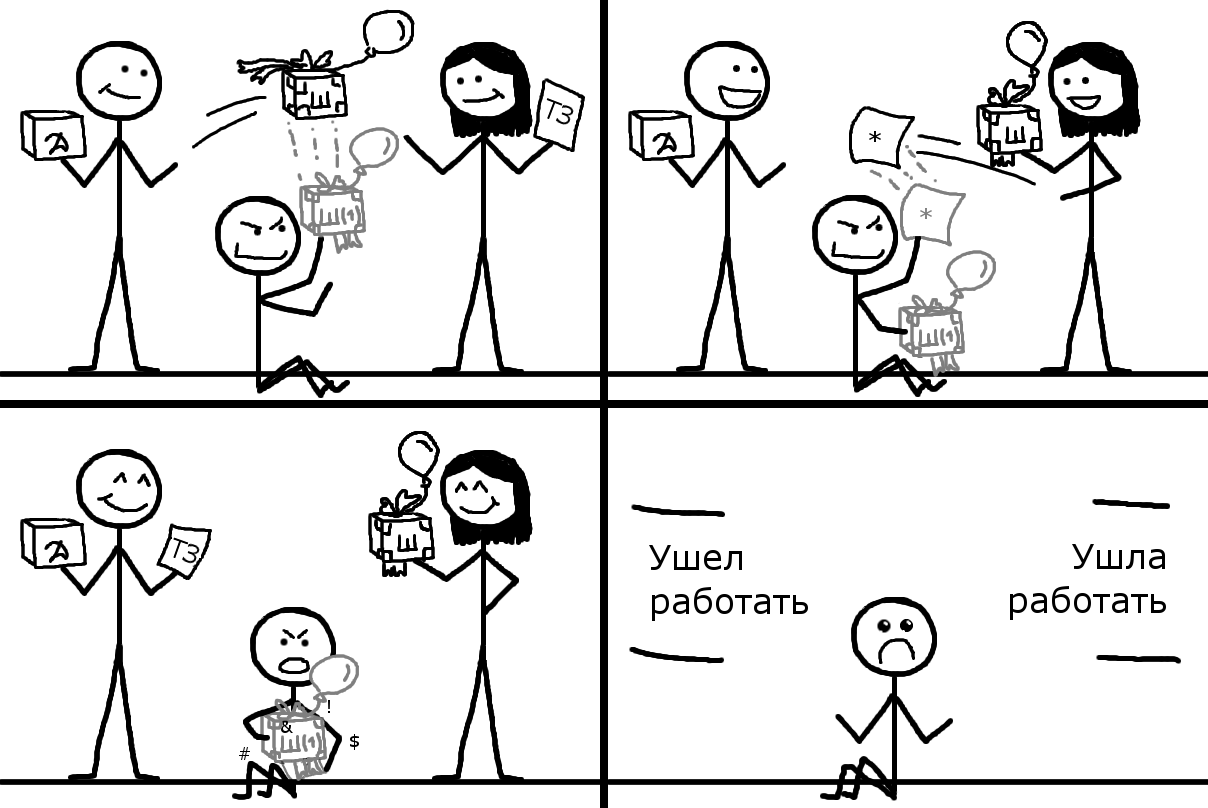
Если и Алёна также умеет делать магию, они могут вполне полноценно общаться друг с другом, сохраняя секретность.
Про игрушку
Рассмотрим игровые автоматы. Известно, что вероятность выиграть на этих устройствах крайне мала, при этом от человека вообще ничего не зависит. Очевидно, что это не есть честно. Так почему бы не исправить это?
Сказано – сделано. Встречайте представителя класса честных азартных игр – «честного однорукого бандита», вероятность выигрыша в котором равняется 100%. Такая вероятность получилась из-за того, что вся информация, которая влияет на успешный исход, находится у играющего перед глазами.
Зачем, спросите вы, автомат, который не приносит выгоды? Все так просто – подход базируется на теории сложности вычислений («complexity theory» — оттуда и было взято название), таким образом, человеку, как уже говорилось, просто-напросто нужно решить NP задачу (здравствуй, полный перебор). А чтобы жизнь медом не казалась, игра идет на время.
Игра содержит два способа шифрования разной сложности — хэширование (много в один) и биекция (один в один). Основной целью нашей игры было объяснение принципа подобного шифрования «на пальцах».
Суть — восстановить (дешифровать) исходные данные над кольцом Z3 (кольцо вычетов по модулю 3), имея перед глазами лишь зашифрованное сообщение и алгоритм шифрования.
Этот алгоритм представляет собой набор узлов с таблицами переходов — у него 2 входа, чьи значения преобразуются, порождая выходное значение. Алгоритм был разбит на узлы неспроста — это и есть обфускация (усложнение), потому что к функции преобразования в явном виде гораздо легче подобрать обратную функцию, из-за чего вся эта NP задача теряет смысл. Суперпозиция же этих узлов и является тем самым алгоритмом шифрования.
Математика
Алгоритм построения биекции, по сути, прост: композиция биекций — биекция, так что нужно только найти способ построения элементарной биекции. В помощь нам пришла аналитическая геометрия — мы шифруем не цвета, а координаты вектора. Умножая матрицу перехода на заданный вектор, мы получаем новый вектор — зашифрованный, а чтобы можно было перейти от полученного к исходному вектору, матрица перехода должна быть обратимой – строим обратную к исходной, умножаем на зашифрованное сообщение и получаем исходные данные. Таким образом, все сводится к построению такой матрицы.
Алгоритм построения хэширования еще проще: строим биекцию, и на каждом слое узлов убираем несколько штук, продолжая так до тех пор, пока не получим необходимое нам количество узлов на конце. То, что этот алгоритм некогда был биекцией, гарантирует нам равномерное распределение, что сводит количество коллизий к минимуму.
Таким образом:
- Исходное сообщение – вектор значений над кольцом Z3 (3 значения, представленных различными цветами);
- Алгоритм шифрования – матрица;
- Обфускация алгоритма – наборы матриц с двумя входами и одним выходом;
- Зашифрованное сообщение – вектор, полученный в результате умножения исходного сообщения на матрицу.
Программирование
Игрушку сделали на Canvas, так что в нее можно поиграть с любого устройства. Писали, конечно, на JavaScript, PHP (для генерации графа), С++ (для его размещения), а также использовали фреймворк KineticJS, чтобы все работало шустрее (но у них какая-то нелюбовь с Firefox, так что там немного тормозит).
Заключение
Как и было обещано, делюсь ссылкой на игрушку, которая была сделана во время работы в лаборатории при университете.
Надеюсь, она достаточно наглядно покажет, что даже простейшие отображения (типа хэш 4-2) достаточно сложны для дешифровки после обфускации.
Всем добра. :3

Автор: Rideto


