Туториал по Unreal Engine 4: фильтр Paint

С течением времени внешний вид игр становится всё лучше и лучше. В эпоху потрясающей графики сложно сделать так, чтобы собственная игра выделялась на фоне остальных. Один из способов сделать игру графически более уникальной — использование нефотореалистичного рендеринга.

Нефотореалистичный рендеринг включает в себя множество техник рендеринга. В них входят cel shading, toon-контуры и штриховка. Можно даже сделать так, что игра будет похожа на картину! Одним из способов получения такого эффекта является размытие фильтром Кавахары.

Для реализации фильтрации Кавахары мы научимся следующему:

• Вычислять среднее и дисперсию для нескольких ядер
• Выводить среднее значение для ядра с наименьшей дисперсией
• Использовать оператор Собеля для нахождения локальной ориентации пикселя
• Поворачивать ядра сэмплирования на основании локальной ориентации пикселя

Примечание: в этом туториале подразумевается, что вы уже знакомы с основами Unreal Engine. Если только осваиваете Unreal Engine, то изучите нашу серию туториалов Unreal Engine для начинающих из десяти частей.

Так как в этом туториале применяется HLSL, вы должны быть знакомы с ним или похожим на него языком, например, с C#.

Примечание: этот туториал является четвёртой частью серии туториалов, посвящённых шейдерам:

• Часть 1: Cel Shading
• Часть 2: Toon-контуры
• Часть 3: Собственные шейдеры на HLSL
• Часть 4: Фильтр Paint

Приступаем к работе

Начните со скачивания материалов для туториала. Распакуйте их, перейдите PaintFilterStarter и откройте PaintFilter.uproject. Вы увидите следующую сцену:

Для экономии времени в сцене уже есть Post Process Volume с PP_Kuwahara. Это материал (и файлы шейдера), которые мы будем изменять.

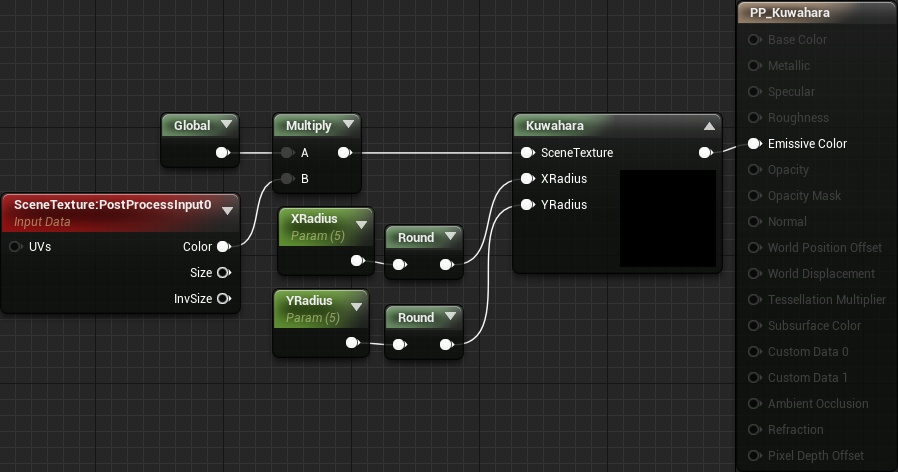
Сначала давайте разберёмся, что такое фильтр Кавахары и как он работает.

Фильтр Кавахары

При съёмке фотографий вы можете заметить на изображении зернистую текстуру. Это шум, который нам совершенно не нужен.

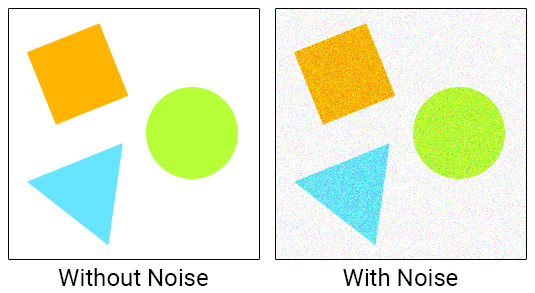
Обычно от шума избавляются использованием фильтра низких частот, например blur. Ниже показано зашумлённое изображение после применения к нему box blur с радиусом 5.

Бо́льшая часть шума исчезла, но все границы потеряли свою резкость. Вот бы существовал фильтр, который мог сгладить изображение и сохранить при этом границы объектов!

Как вы могли уже догадаться, фильтр Кавахары соответствует всем этим требованиям. Давайте посмотрим, как он работает.

Как работает фильтрация Кавахары

Как и в свёртках, при фильтрации Кавахары применяются ядра, но вместо одного ядра используется четыре. Ядра расставлены таким образом, что перекрываются в одном пикселе (в текущем). Ниже показан пример ядер для фильтра Кавахары.

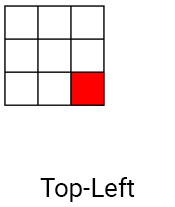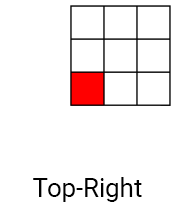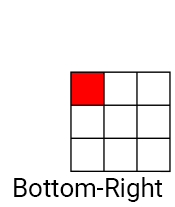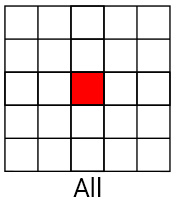
Сначала мы вычисляем среднее (средний цвет) для каждого ядра. Так мы размываем ядро, то есть сглаживаем шум.

Также для каждого ядра мы вычисляем дисперсию. По сути, это мера того, насколько варьируется цвет в ядре. Например, у ядра с близкими цветами будет низкая дисперсия. Если цвета различны, то дисперсия ядра будет высокой.

Примечание: если вы не знакомы с концепцией дисперсии или не знаете, как её вычислять, то изучите статью Standard Deviation and Variance на Math is Fun.

Наконец, мы находим ядро с наименьшей дисперсией и выводим его среднее значение. Именно благодаря выбору на основании дисперсии фильтр Кавахары позволяет сохранять границы. Давайте рассмотрим несколько примеров.

Примеры фильтрации Кавахары

Ниже показано изображение в оттенках серого размером 10×10. Видно, что на нём есть граница, идущая из левого нижнего в верхний правый угол. Также можно заметить, что в некоторых областях изображения присутствует шум.

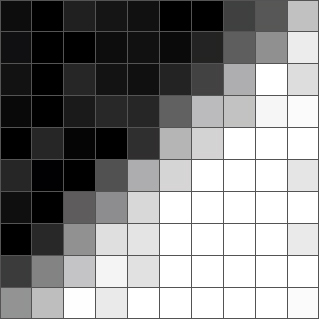
Сначала мы выберем пиксель и определим, какое ядро имеет наименьшую дисперсию. Вот пиксель рядом с границей и связанные с ним ядра:

Как вы видите, у ядер, лежащих на границе, сильно варьируются цвета. Это говорит нам о высокой дисперсии и означает, что фильтр не будет их выбирать. Избегая выбора ядер, лежащих на границе, фильтр устраняет проблему размытых границ.

Для этого пикселя фильтр выберет зелёное ядро, потому что оно является наиболее однородным. Выходным значением тогда будет среднее значение для зелёного ядра, то есть цвет, близкий к чёрному.

Вот ещё один пиксель границы и его ядра:

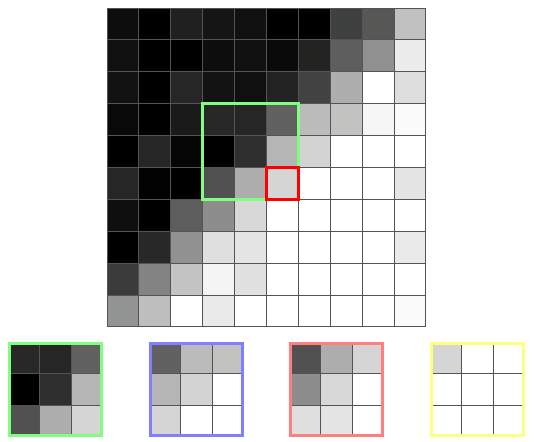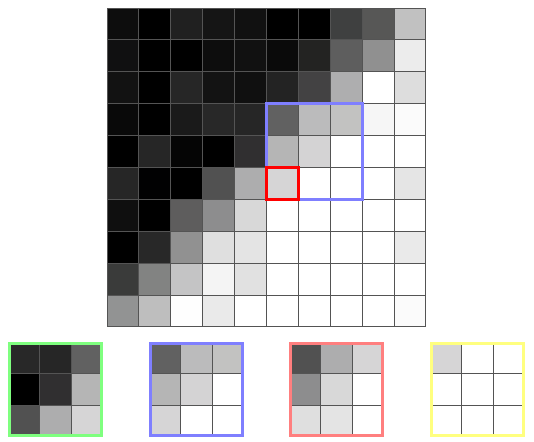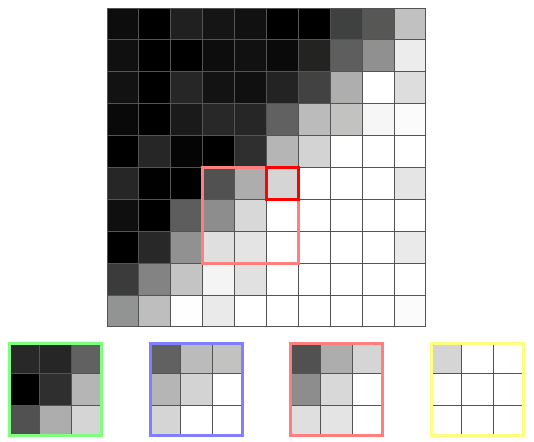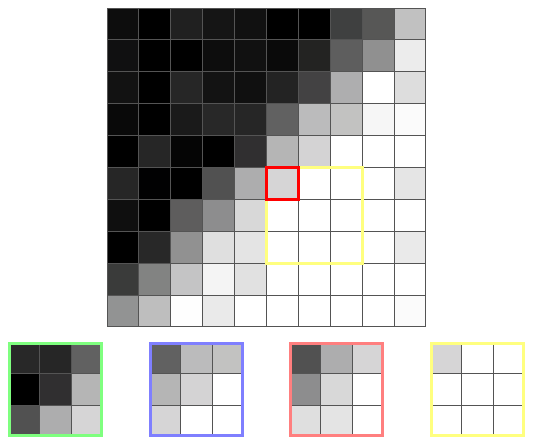
На этот раз наименьшую дисперсию имеет жёлтое ядро, потому что оно единственное не находится на границе. Поэтому выходным значением будет среднее жёлтого ядра, то есть цвет, близкий к белому.

Ниже показано сравнение между box blur и фильтрацией Кавахары с радиусом 5.

Как видите, фильтрация Кавахары замечательно справляется со сглаживанием и сохранением границ. В нашем случае фильтр даже сделал границу резче!

Так совпало, что эта функция сглаживания с сохранением границ может придать изображению вид нарисованной картины. Так как у мазков кисти обычно получаются резкие границы и низкий шум, фильтр Кавахары оказывается удобным выбором для преобразования реалистичных изображений в художественный стиль.

Вот результат выполнения для фотографии фильтрации Кавахары с переменным размером:

Выглядит довольно красиво, правда? Давайте приступим к созданию фильтра Кавахары.

Создание фильтра Кавахары

В этом туториале фильтр разбит на два файла шейдера: Global.usf и Kuwahara.usf. В первом файле будет храниться функция вычисления среднего значения и дисперсии ядра. Второй файл — это входная точка фильтра, которая будет вызывать вышеупомянутую функцию для каждого ядра.

Сначала мы создадим функцию для вычисления среднего значения и дисперсии. Откройте папку проекта в ОС и перейдите в папку Shaders. Затем откройте Global.usf. Внутри вы найдёте функцию GetKernelMeanAndVariance().

Прежде чем приступать к созданию функции, нам необходим дополнительный параметр. Измените сигнатуру функции следующим образом:

float4 GetKernelMeanAndVariance(float2 UV, float4 Range)

Для сэмплирования сетки нам понадобится два цикла for: один — для горизонтальных смещений. второй — для вертикальных. В первых двух каналах Range будут содержаться границы горизонтального цикла. Во вторых двух будут содержаться границы вертикального цикла. Например, если мы сэмплируем верхнее левое ядро, а фильтр имеет радиус 2, то Range будет иметь значения:

Range = float4(-2, 0, -2, 0);

Теперь настало время приступать к сэмплированию.

Сэмплирование пикселей

Для начала нам нужно создать два цикла for. Добавьте в GetKernelMeanAndVariance() следующий код (под переменными):

for (int x = Range.x; x <= Range.y; x++)
{
    for (int y = Range.z; y <= Range.w; y++)
    {
        
    }
}

Это даст нам все смещения ядра. Например, если мы сэмплируем верхнее левое ядро и фильтр имеет радиус 2, то смещения будут находиться в интервале от (0, 0) до (-2, -2).

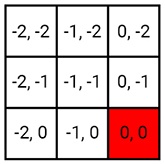
Теперь нам нужно получить цвет пикселя выборки. Добавьте во внутренний цикл for следующий код:

float2 Offset = float2(x, y) * TexelSize;
float3 PixelColor = SceneTextureLookup(UV + Offset, 14, false).rgb;

Первая строка получает смещение пикселя выборки и преобразует его в UV-пространство. Вторая строка использует смещение для получения цвета пикселя выборки.

Теперь нам нужно вычислить среднее значение и дисперсию.

Вычисление среднего значения и дисперсии

Вычисление среднего — достаточно простая задача. Мы просто суммируем все цвета и делим их на количество пикселей выборки. Для дисперсии мы используем показанную ниже формулу, где x — это цвет пикселя выборки:

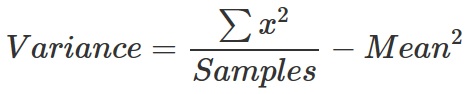
Первое, что нам нужно сделать — вычислить суммы. Для получения среднего нам достаточно сложить цвета в переменной Mean. Для получения дисперсии нам нужно возвести цвет в квадрат, а затем прибавить его к Variance. Добавьте следующий код под предыдущим:

Mean += PixelColor;
Variance += PixelColor * PixelColor;
Samples++;

Далее добавьте следующее после циклов for:

Mean /= Samples;
Variance = Variance / Samples - Mean * Mean;
float TotalVariance = Variance.r + Variance.g + Variance.b;
return float4(Mean.r, Mean.g, Mean.b, TotalVariance);

Первые две строки вычисляют среднее и дисперсию. Однако возникает проблема: дисперсия распределена между каналами RGB. Чтобы решить её, в третьей строке мы суммируем каналы, чтобы получить общую дисперсию.

В конце функция возвращает среднее и дисперсию в виде float4. Среднее значение находится в каналах RGB, а дисперсия — в канале A.

Теперь, когда у нас есть функция для вычисления среднего значения и дисперсии, нам нужно вызвать её для каждого ядра. Вернитесь в папку Shaders и откройте Kuwahara.usf. Сначала нам нужно создать несколько переменных. Замените код внутри на следующий:

float2 UV = GetDefaultSceneTextureUV(Parameters, 14);
float4 MeanAndVariance[4];
float4 Range;

Вот, для чего используется каждая переменная:

• UV: UV-координаты текущего пикселя
• MeanAndVariance: массив для хранения среднего и дисперсии каждого ядра
• Range: используется для хранения границ циклов for текущего ядра

Теперь нам нужно вызвать для каждого ядра GetKernelMeanAndVariance(). Для этого добавим следующее:

Range = float4(-XRadius, 0, -YRadius, 0);
MeanAndVariance[0] = GetKernelMeanAndVariance(UV, Range);

Range = float4(0, XRadius, -YRadius, 0);
MeanAndVariance[1] = GetKernelMeanAndVariance(UV, Range);

Range = float4(-XRadius, 0, 0, YRadius);
MeanAndVariance[2] = GetKernelMeanAndVariance(UV, Range);

Range = float4(0, XRadius, 0, YRadius);
MeanAndVariance[3] = GetKernelMeanAndVariance(UV, Range);

Так мы получим среднее и дисперсию каждого ядра в следующем порядке: верхнее левое, верхнее правое, нижнее левое и нижнее правое.

Далее нам нужно выбрать ядро с наименьшей дисперсией и вывести его среднее значение.

Выбор ядра с наименьшей дисперсией

Чтобы выбрать ядро с наименьшей дисперсией, добавьте следующий код:

// 1
float3 FinalColor = MeanAndVariance[0].rgb;
float MinimumVariance = MeanAndVariance[0].a;

// 2
for (int i = 1; i < 4; i++)
{
    if (MeanAndVariance[i].a < MinimumVariance)
    {
        FinalColor = MeanAndVariance[i].rgb;
        MinimumVariance = MeanAndVariance[i].a;
    }
}

return FinalColor;

Вот, что делает каждая из частей:

1. Создаёт две переменные для хранения конечного цвета и наименьшей дисперсии. Инициализирует их обе со значениями среднего и дисперсии первого ядра.
2. Обходит в цикле оставшиеся три ядра. Если дисперсия текущего ядра ниже наименьшего, то его среднее и дисперсия становятся новыми FinalColor и MinimumVariance. После выполнения циклов выводится FinalColor который будет средним значением ядра с наименьшей дисперсией.

Вернитесь в Unreal и перейдите к MaterialsPostProcess. Откройте PP_Kuwahara, внесите ни на что не влияющие изменения и нажмите Apply. Вернитесь в основной редактор и посмотрите на результаты!

Выглядит довольно неплохо, но если приглядеться, то можно увидеть, что на изображении присутствуют странные блочные области. Я выделил некоторые из них:

Это побочный эффект применения ядер, выровненных относительно осей. Мы можем уменьшить этот эффект, применив улучшенную версию фильтра, которую я называю направленным фильтром Кавахары.

Направленный фильтр Кавахары

Этот фильтр похож на исходный, но теперь ядра будут выровнены относительно локальной ориентации пикселей. Вот пример ядра в направленном фильтре Кавахары:

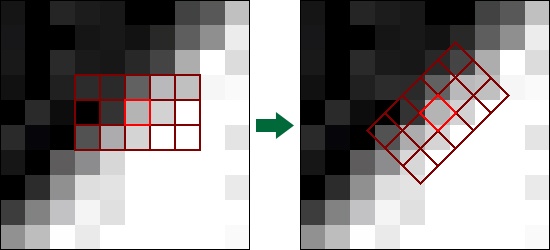
Примечание: так как мы можем представить ядро в виде матрицы, мы записываем измерения в виде высота x ширина вместо привычного ширина x высота. Подробнее о матрицах мы поговорим ниже.

Здесь фильтр определяет ориентацию пикселя так, чтобы он располагался вдоль границы. После чего можно соответствующим образом повернуть всё ядро.

Для вычисления локальной ориентации фильтр выполняет проход свёртки с помощью оператора Собеля. Если термин «оператор Собеля» звучит для вас знакомо, то это потому, что он является популярной техникой распознавания границ. Но если это приём распознавания границ, то как можно использовать его для получения локальной ориентации? Чтобы ответить на этот вопрос, нам нужно понять, как работает оператор Собеля.

Как работает оператор Собеля

Вместо одного ядра в операторе Собеля используется два.

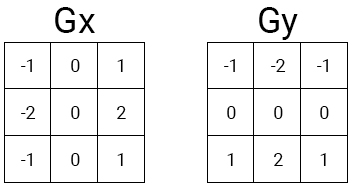
Gx даёт нам градиент в горизонтальном направлении. Gy даёт нам градиент в вертикальном направлении. Давайте воспользуемся в качестве примера таким изображением в оттенках серого размером 3×3:

Для начала выполним свёртку среднего пикселя для каждого ядра.

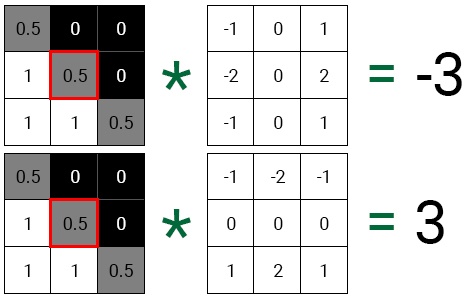
Если нанести каждое значение на 2D-плоскость, то мы увидим, что получившийся вектор указывает в том же направлении, что и граница.

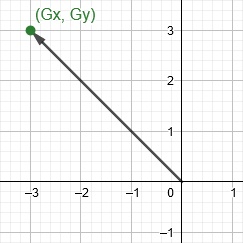
Чтобы найти угол между вектором и осью X, мы подставляем значения градиентов в функцию арктангенса (atan). После чего мы можем использовать получившийся угол для поворота ядра.

Именно так мы можем использовать оператор Собеля для получения локальной ориентации пикселя. Давайте попробуем это сделать.

Нахождение локальной ориентации

Откройте Global.usf и добавьте внутрь GetPixelAngle() следующий код:

float GradientX = 0;
float GradientY = 0;
float SobelX[9] = {-1, -2, -1, 0, 0, 0, 1, 2, 1};
float SobelY[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
int i = 0;

Примечание: Заметьте, что последняя скобка в GetPixelAngle() отсутствует. Это сделано намеренно! Если хотите знать, зачем так делать, прочитайте наш туториал по шейдерам на HLSL.

Вот, для чего используется каждая переменная:

• GradientX: хранит градиент для горизонтального направления
• GradientY: хранит градиент для вертикального направления
• SobelX: ядро горизонтального оператора Собеля в виде массива
• SobelY: ядро вертикального оператора Собеля в виде массива
• i: используется для доступа к каждому элементу в SobelX и SobelY

Далее нам необходимо выполнить свёртку с помощью ядер SobelX и SobelY. Добавьте следующий код:

for (int x = -1; x <= 1; x++)
{
    for (int y = -1; y <= 1; y++)
    {
        // 1
        float2 Offset = float2(x, y) * TexelSize;
        float3 PixelColor = SceneTextureLookup(UV + Offset, 14, false).rgb;
        float PixelValue = dot(PixelColor, float3(0.3,0.59,0.11));
        
        // 2
        GradientX += PixelValue * SobelX[i];
        GradientY += PixelValue * SobelY[i];
        i++;
    }
}

Вот, что происходит в каждой части:

1. Первые две строки получают цвет пикселя выборки. Третья строка снижает насыщенность цвета, преобразуя его в значение оттенков серого. Это упрощает вычисление градиентов изображения в целом, вместо получения градиентов для каждого цветового канала.
2. Для обоих ядер умножаем значение пикселя в оттенках серого на соответствующий элемент ядра. Затем прибавляем результат к соответствующей переменной градиента. Затем происходит инкремент i, чтобы она содержала в себе индекс следующего элемента ядра.

Для получения угла мы используем функцию atan() и подставляем наши значения градиентов. Под циклами for добавьте следующий код:

return atan(GradientY / GradientX);

Теперь, когда у нас есть функция для получения угла пикселя, нужно каким-то образом применить его для поворота ядра. Мы можем сделать это с помощью матрицы.

Что такое матрица?

Матрица — это двухмерный массив чисел. Например, вот матрица 2×3 (с двумя строками и тремя столбцами):

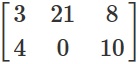
Сама по себе матрица не выглядит особо интересной. Но истинная мощь матриц проявляется, когда мы перемножаем её с вектором. Это позволяет нам выполнять такие действия, как поворот и масштабирование (в зависимости от вида матрицы). Но как же нам создать матрицу для поворота?

В системе координат у нас есть вектор для каждого измерения. Это базисные векторы, определяющие положительные направления осей.

Ниже представлено несколько примеров разных базисных векторов для двухмерной системы координат. Красной стрелкой показано положительное направление по X. Зелёная стрелка задаёт положительное направление по Y.

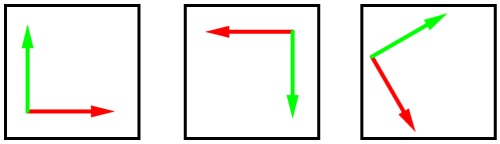
Чтобы повернуть вектор, мы можем использовать эти базисные векторы для построения матрицы поворота. Она является просто матрицей, содержащей позиции базисных векторов после поворота. Например, представьте, что у нас есть вектор (оранжевая стрелка) в координатах (1, 1).

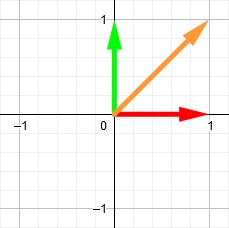
Допустим, мы хотим повернуть его на 90 градусов по часовой стрелке. Сначала мы поворачиваем на ту же величину базисные векторы.

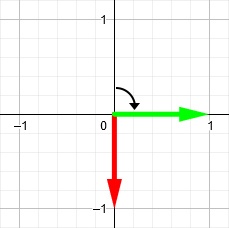
Затем мы строим матрицу 2×2, применяя новые позиции базисных векторов. Первый столбец — это позиция красной стрелки, а второй — позиция зелёной стрелки. Это и есть наша матрица поворота.

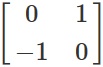
Наконец, мы выполняем матричное умножение, используя оранжевый вектор и матрицу поворота. Результат будет новой позицией оранжевого вектора.

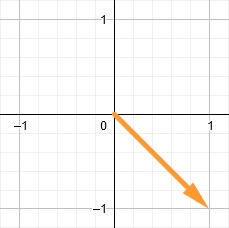
Примечание: вам необязательно знать, как выполняется матричное умножение, потому что в HLSL есть для этого встроенная функция. Но если вы хотите узнать, то изучите статью How to Multiply Matrices на Math is Fun.

Разве это не здорово? Но ещё лучше то, что мы можем использовать показанную выше матрицу для поворота любого 2D-вектора на 90 градусов по часовой стрелке. Если говорить о нашем фильтре, то это значит, что нам достаточно один раз создать матрицу поворота для каждого пикселя и использовать её для всего ядра.

Теперь настало время поворота ядра с помощью матрицы поворота.

Поворот ядра

Для начала нам нужно изменить GetKernelMeanAndVariance(), чтобы она получала матрицу 2×2. Это нужно потому, что мы будем создавать матрицу поворота в Kuwahara.usf и передавать её. Измените сигнатуру GetKernelMeanAndVariance() следующим образом:

float4 GetKernelMeanAndVariance(float2 UV, float4 Range, float2x2 RotationMatrix)

Далее замените первую строку внутреннего цикла for на такой код:

float2 Offset = mul(float2(x, y) * TexelSize, RotationMatrix);

mul() будет выполнять матричное умножение, используя смещение и RotationMatrix. Так мы будем поворачивать смещение вокруг текущего пикселя.

Далее нам нужно создать матрицу поворота.

Создание матрицы поворота

Для создания матрицы поворота мы применим функции синуса и косинуса следующим образом:

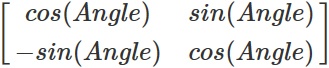
Закройте Global.usf и откройте Kuwahara.usf. Затем добавьте под списком переменных следующее:

float Angle = GetPixelAngle(UV);
float2x2 RotationMatrix = float2x2(cos(Angle), -sin(Angle), sin(Angle), cos(Angle));

В первой строке вычисляется угол текущего пикселя. Вторая строка создаёт матрицу поворота с использованием угла.

Наконец, нам нужно передать для каждого ядра RotationMatrix. Измените каждый вызов GetKernelMeanAndVariance() следующим образом:

GetKernelMeanAndVariance(UV, Range, RotationMatrix)

И на этом мы закончили создание направленного фильтра Кавахары! Закройте Kuwahara.usf и вернитесь в PP_Kuwahara. Внесите ни на что не влияющие изменения, нажмите Apply и закройте его.

Ниже показано изображение со сравнением обычного и направленного фильтров Кавахары. Заметьте, что направленный фильтр не создаёт блочности.

Примечание: можно использовать PPI_Kuwahara для изменения размеров фильтра. Рекомендую изменить размер фильтра таким образом, чтобы радиус по X был больше, чем радиус по Y. Это увеличит размер ядра вдоль границы и поможет в создании направленности.

Куда двигаться дальше?

Скачать готовый проект можно по ссылке.

Если вы хотите больше узнать о фильтре Кавахары, то можете прочитать статью про анизотропную фильтрацию Кавахары. На самом деле направленный фильтр Кавахары является упрощённой версией фильтра, представленного в этой статье.

Рекомендую вам поэкспериментировать с матрицами, чтобы с помощью них попробовать создать новые эффекты. Например, можно использовать сочетание матриц поворота и размытия (blurring) для создания радиального или кругового размытия. Если вы хотите больше узнать о матрицах и о том, как они работают, то изучите серию видео 3Blue1Brown Essence of Linear Algebra.

Автор: PatientZero

Источник