Глубокое обучение с использованием R и mxnet. Часть 1. Основы работы

Привет!

Эта статья является первой частью руководства по приготовления нейронных сетей с использованием библиотеки mxnet на языке R. Источником вдохновения послужила онлайн-книга Deep Learning — The Straight Dope, объема которой достаточно для осознанного использования mxnet на Питоне. Примеры оттуда будут воспроизводиться с поправкой на отсутствие реализации интерфейса Gluon для R. В первой части рассмотрим установку библиотеки и общие принципы работы, а также реализуем простую линейную модель для решения задачи регрессии.

Содержание:

1. Установка библиотеки mxnet
2. Используемый набор данных
3. Основная функция для обучения нейросетей
4. Итераторы
5. Архитектура сети
6. Инициализатор
7. Оптимизатор
8. Функции обратного вызова (колбэки)
9. Обучение модели
10. Решение задачи регрессии на реальных данных

1. Установка библиотеки mxnet

Понятное руководство по установке разных версий (CPU/GPU) для разных языков и под разные устройства появилось относительно недавно. Подготовительные этапы типа установки драйверов и CUDA/cuDNN были рассмотрены в этом сообщении, повторяться не будем. Для Python, кстати, можно ничего не собирать из исходников, а просто ставить командой pip install mxnet --pre. В ситуации, когда ядер CPU относительно много, а ОЗУ относительно мало, при сборке из исходников можно столкнуться с нехваткой памяти. В таком случае следует запустить сборку в однопоточном режиме: make -j1.

Библиотеку можно использовать также в коде на языках Julia, Scala и, внезапно, Perl. А еще заявлена поддержка работы на Raspberry Pi 3.

2. Используемый набор данных

Создадим искусственный набор данных из 10000 наблюдений (num_examples) с двумя признаками (num_inputs) и одной целевой переменной (num_outputs). Истинная форма зависимости между предикторами и целевой переменной задана функцией real_fn(), к сгенерированных при помощи этой функции значениям добавлен небольшой гауссовский шум 0.01 * rnorm(num_examples):

num_inputs <- 2
num_outputs <- 1
num_examples <- 10000

real_fn <- function(x) {
  2 * x[, 1] - 3.4 * x[, 2] + 4.2
}

X <- matrix(rnorm(num_examples * num_inputs), 
            ncol = num_inputs)

noise <- 0.01 * rnorm(num_examples)

y <- real_fn(X) + noise

3. Основная функция для обучения нейросетей

За обучение нейросетей прямого распространения отвечает функция mx.model.FeedForward.create(). Список принимаемых ею параметров выглядит следующим образом:

• symbol — архитектура сети в виде символьного описания. Это не совсем граф вычислений, поскольку в нем не заданы размерности тензоров и функция потерь, но что-то похожее. Архитектуру можно нарисовать при помощи функции graph.viz(), пример будет ниже;
• X — матрица/массив или итератор данных, используемых для обучения. Массивы используем, когда данные целиком помещаются в память, а итераторы — когда не помещаются. Есть несколько готовых итераторов (по массивам, по картинкам в бинарном формате RecordIO, по csv-файлам) и возможность создавать свои собственные;
• y — значения целевой переменной. Задается только в случае, когда X является массивом, в противном случае итератор должен возвращать все необходимое для обучения, включая правильные ответы;
• ctx — устройство или список устройств, используемых для обучения (CPU/GPU). Объект класса MXContext, создаваемый при помощи mx.cpu() или mx.gpu();
• begin.round — начальное значение счетчика итераций (эпох) обучения. Менять значение по умолчанию (1) нужно только при дообучении модели;
• num.round — количество эпох;
• optimizer — используемый оптимизатор, заданный по имени (в виде строки). По умолчанию — стохастический градиентный спуск ("sgd"). Пример настройки параметров оптимизатора представлен ниже;
• initializer — объект, задающий схему инициализации параметров модели;
• eval.data — список вида list(data = R.array, label = R.array) или итератор с валидационными данными;
• eval.metric — функция для оценка качества модели. Помимо доступных вариантов можно также использовать собственноручно написанную;
• epoch.end.callback — функция, запускаемая после каждой эпохи обучения;
• batch.end.callback — функция, запускаемая после каждого батча;
• array.batch.size — размер батча при использовании данных в виде массива. При использовании итераторов размер мбатча в них же и задается;
• array.layout — "auto", "colmajor" или "rowmajor" (по умолчанию — "auto"). Формат массивов: для матрицы "rowmajor" означает, что dim(X) = c(nexample, nfeatures), а "colmajor" — что dim(X) = c(nfeatures, nexample). Формат "rowmajor" допустим только для матриц. Функция mx.io.arrayiter() в явном виде потребует преобразовать данные к формату "colmajor", т.е. матрица будет транспонированной по отношению к привычному виду с наблюдениями в строках и признаками в столбцах;
• kvstore — задается в виде строки и отвечает за схему синхронизации при обучении на нескольких устройства. По умолчанию равен "local";
• verbose — отвечает за вывод информационных сообщений в процессе обучения. По умолчанию равен TRUE;
• arg.params — опциональный параметр со списком массивов NDArray, содержащих веса модели;
• aux.params — аналогичный список дополнительных параметров;
• input.names — имена символов, подаваемых на вход;
• output.names — имена символов, получаемых на выходе;
• fixed.param — параметры, которые остаются фиксированными в ходе обучения (не обучаются);
• allow.extra.params — разрешает передавать дополнительные параметры, которые не требуются согласно символьному описанию модели. Если задать равным TRUE, при наличии таких лишних параметров в списках arg.params и aux.params ошибка появляться не будет.

4. Итераторы

Создадим итератор по массиву (матрице) данных:

batch_size <- 4

train_data <- mx.io.arrayiter(t(X), 
                              y, 
                              batch.size = batch_size, 
                              shuffle = TRUE)

Функция принимает на вход массив или матрицу признаков (в данном случае, как уже было сказано, матрицу нужно транспонировать), массив со значениями целевой переменной и размер батча. Также мы включили перемешивание наблюдений опцией shuffle = TRUE. Список всех доступных итераторов выглядит так:

apropos("mx.io")

 # [1] "mx.io.arrayiter"               "mx.io.bucket.iter"            
 # [3] "mx.io.CSVIter"                 "mx.io.extract"                
 # [5] "mx.io.ImageDetRecordIter"      "mx.io.ImageRecordIter"        
 # [7] "mx.io.ImageRecordIter_v1"      "mx.io.ImageRecordUInt8Iter"   
 # [9] "mx.io.ImageRecordUInt8Iter_v1" "mx.io.LibSVMIter" 

Сейчас мы не будем рассматривать ни остальные варианты, ни написание собственных итераторов.

5. Архитектура сети

Архитектура сети описывается путем последовательных вызовов функций семейства mx.symbol.*, каждая из которых добавляет к модели абстрактные представления слоев: полносвязного, сверточного, пулингового и других. Слоев доступно очень много:

apropos("mx.symbol")

#   [1] "is.mx.symbol"                                  
#   [2] "mx.symbol.abs"                                 
#   [3] "mx.symbol.Activation"                          
#   [4] "mx.symbol.adam_update"                         
#   [5] "mx.symbol.add_n"                               
# .....                      
# [208] "mx.symbol.transpose"                           
# [209] "mx.symbol.trunc"                               
# [210] "mx.symbol.uniform"                             
# [211] "mx.symbol.UpSampling"                          
# [212] "mx.symbol.Variable"                            
# [213] "mx.symbol.where"                               
# [214] "mx.symbol.zeros_like"

Для создания простой линейной модели, решающей задачу регрессии, служит следующий код:

data <- mx.symbol.Variable("data")
fc1 <- mx.symbol.FullyConnected(data, 
                                num_hidden = 1)
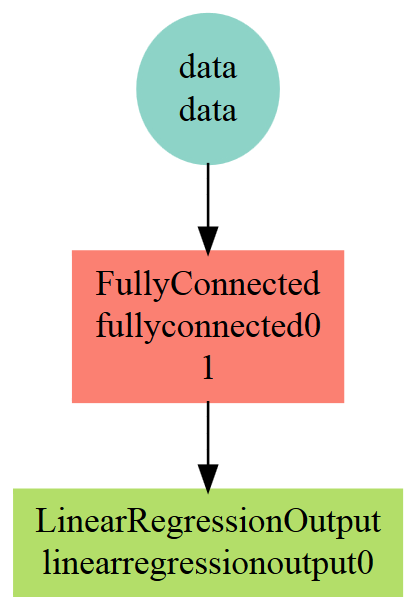
linreg <- mx.symbol.LinearRegressionOutput(fc1)

Нарисуем получившуюся архитектуру:

graph.viz(linreg)

6. Инициализатор

Инициализатор определяет, с каких начальных значений стартует обучение нейросети. Поскольку наша сеть очень простая и неглубокая, достаточно инициализировать веса случайными значениями, имеющими нормальное распределение:

initializer <- mx.init.normal(sd = 0.1)

Единственным принимаемым параметров в данном случае является стандартное отклонение. Также имеется инициализатор mx.init.uniform(), единственным параметром которого является граница диапазона, из которого генерируются значения.

Для глубоких сетей правильная инициализация весов имеет большое значение, поэтому мы бы воспользовались вариантом mx.init.Xavier().

Эта схема инициализации весов была придумана в 2010 году Йошуа Бенджио и Ксавье Глоро (Xavier Gloro), в честь которого метод и получил свое название. В настоящий момент используется повсеместно под разными именами, например, в Keras можно найти glorot_normal glorot_uniform. Библиотека для Python содержит также множество других инициализаторов, недоступных в варианте для R. Например, отсутствует возможность использовать предпочтительный вариант инициалиализции весов нейронов с функцией активации ReLU — инициализацию Хе.

Параметры функции mx.init.Xavier():

• rnd_type — строка, задающая вид распределения ("uniform" или "gaussian"), из которого будут генерироваться веса;
• factor_type — "avg", "in" или "out" (см. ниже);
• magnitude — не совсем понятный числовой параметр, задающий масштаб получаемых весов.

Если rnd_type = "uniform" и factor_type = "avg" (по умолчанию), веса будут инициализированы случайными значениями из диапазона , где , — число нейронов на входе (т.е. в предыдущем слое), — число нейронов на выходе (т.е. в следующем слое).

Если rnd_type = "uniform" и factor_type = "in, то . Аналогично, при rnd_type = "uniform" и factor_type = "out" получим .

При rnd_type = "gaussian" и factor_type = "avg" веса будут извлекаться из нормального распределения со стандартным отклонением .

7. Оптимизатор

Оптимизатор определяет способ обновления весов сети. Доступные варианты: sgd, rmsprop, adam, adagrad и adadelta. Создать оптимизатор с нужными настройками можно при помощи общей функции mx.opt.create():

optimizer <- mx.opt.create("sgd", 
                           learning.rate = 2e-5,
                           momentum = 0.9)

Чтобы узнать о параметрах каждого из оптимизаторов, которые будем передавать в вызов mx.opt.create(), воспользуемся справкой:

?mx.opt.sgd
?mx.opt.rmsprop
?mx.opt.adam
?mx.opt.adagrad
?mx.opt.adadelta

Сами эти функции привычным способом вызвать нельзя (но к ним можно получить доступ: mxnet:::mx.opt.adagrad).

Параметры mx.opt.sgd()

• learning.rate — скорость обучения;
• momentum — момент;
• wd — коэффициент l2-регуляризации (добавляет штраф за большие веса);
• rescale.grad — значение, на которое умножается полученный градиент перед обновлением весов. Часто берется равным 1 / batch_size;
• clip_gradient — ограничение величин градиентов путем их проекции на интервал ;
• lr_scheduler — планировщик изменения скорость обучения.

Параметры mx.opt.rmsprop()

• learning.rate — скорость обучения;
• gamma1 — коэффициент затухания для скользящего среднего квадратов градиентов;
• gamma2 — момент;
• wd — коэффициент l2-регуляризации (добавляет штраф за большие веса);
• rescale.grad — значение, на которое умножается полученный градиент перед обновлением весов. Часто берется равным 1 / batch_size;
• clip_gradient — ограничение величин градиентов путем их проекции на интервал ;
• lr_scheduler — планировщик изменения скорость обучения.

Параметры mx.opt.adadelta():

• rho — коэффициент затухания для квадратов градиентов и квадратов обновлений параметров;
• epsilon — маленькая константа (1e-05), чтобы избежать деления на 0;
• wd — коэффициент l2-регуляризации (добавляет штраф за большие веса);
• rescale.grad — значение, на которое умножается полученный градиент перед обновлением весов. Часто берется равным 1 / batch_size;
• clip_gradient — ограничение величин градиентов путем их проекции на интервал .

Обратите внимание: для скорости обучения параметр не предусмотрен.

Оптимизатор Adadelta похож на RMSprop, но Adadelta делает вторую поправку с изменением единиц и хранением истории обновлений, а RMSprop просто использует корень из среднего от квадратов градиентов. Следующий алгоритм — Adagrad — использует сглаженные версии среднего и среднеквадратичного градиентов. Подробнее обо всем этом можно прочитать в книге Глубокое обучение, которая рекомендуется к прочтению целиком.

Параметры mx.opt.adagrad():

• learning.rate — скорость обучения;
• epsilon — маленькая константа (1e-08), чтобы избежать деления на 0;
• wd — коэффициент l2-регуляризации (добавляет штраф за большие веса);
• rescale.grad — значение, на которое умножается полученный градиент перед обновлением весов. Часто берется равным 1 / batch_size;
• clip_gradient — ограничение величин градиентов путем их проекции на интервал ;
• lr_scheduler — планировщик изменения скорость обучения.

Параметры mx.opt.adam():

• learning.rate — скорость обучения;
• beta1 — коэффициент затухания для первой оценки момента;
• beta2 — коэффициент затухания для второй оценки момента;
• epsilon — маленькая константа (1e-08), чтобы избежать деления на 0;
• wd — коэффициент l2-регуляризации (добавляет штраф за большие веса);
• rescale.grad — значение, на которое умножается полученный градиент перед обновлением весов. Часто берется равным 1 / batch_size;
• clip_gradient — ограничение величин градиентов путем их проекции на интервал ;
• lr_scheduler — планировщик изменения скорость обучения.

8. Функции обратного вызова (колбэки)

Сохранять историю обучения будем при помощи соответствующей callback-функции:

logger <- mx.metric.logger()
epoch.end.callback <- mx.callback.log.train.metric(
    period = 1, # число батчей, после которого оценивается метрика
    logger = logger)

После обучения объект logger будет содержать информацию вида

logger$train
# [1] 2.322148818 0.318418684 0.044898842 0.011428233 0.009461375

Другие колбэки: mx.callback.early.stop() отвечает за раннюю остановку, mx.callback.log.speedometer() выводит скорость обработки с заданной частотой, mx.callback.save.checkpoint() сохраняет модель через заданные промежутки в файл с заданным префиксом.

9. Обучение модели

Обучение запускается вызовом описанной выше функции mx.model.FeedForward.create():

model <- mx.model.FeedForward.create(
    symbol = linreg, 
    X = train_data, 
    ctx = mx.cpu(), 
    num.round = 5, 
    initializer = initializer, 
    optimizer = optimizer,
    eval.metric = mx.metric.rmse,
    epoch.end.callback = epoch.end.callback)

## Start training with 1 devices

## [1] Train-rmse=2.39517188021255

## [2] Train-rmse=0.34100598193831

## [3] Train-rmse=0.0498822148288494

## [4] Train-rmse=0.0120600163293274

## [5] Train-rmse=0.00946668211065784

Изобразим историю обучения:

plot(logger$train, type = "l")

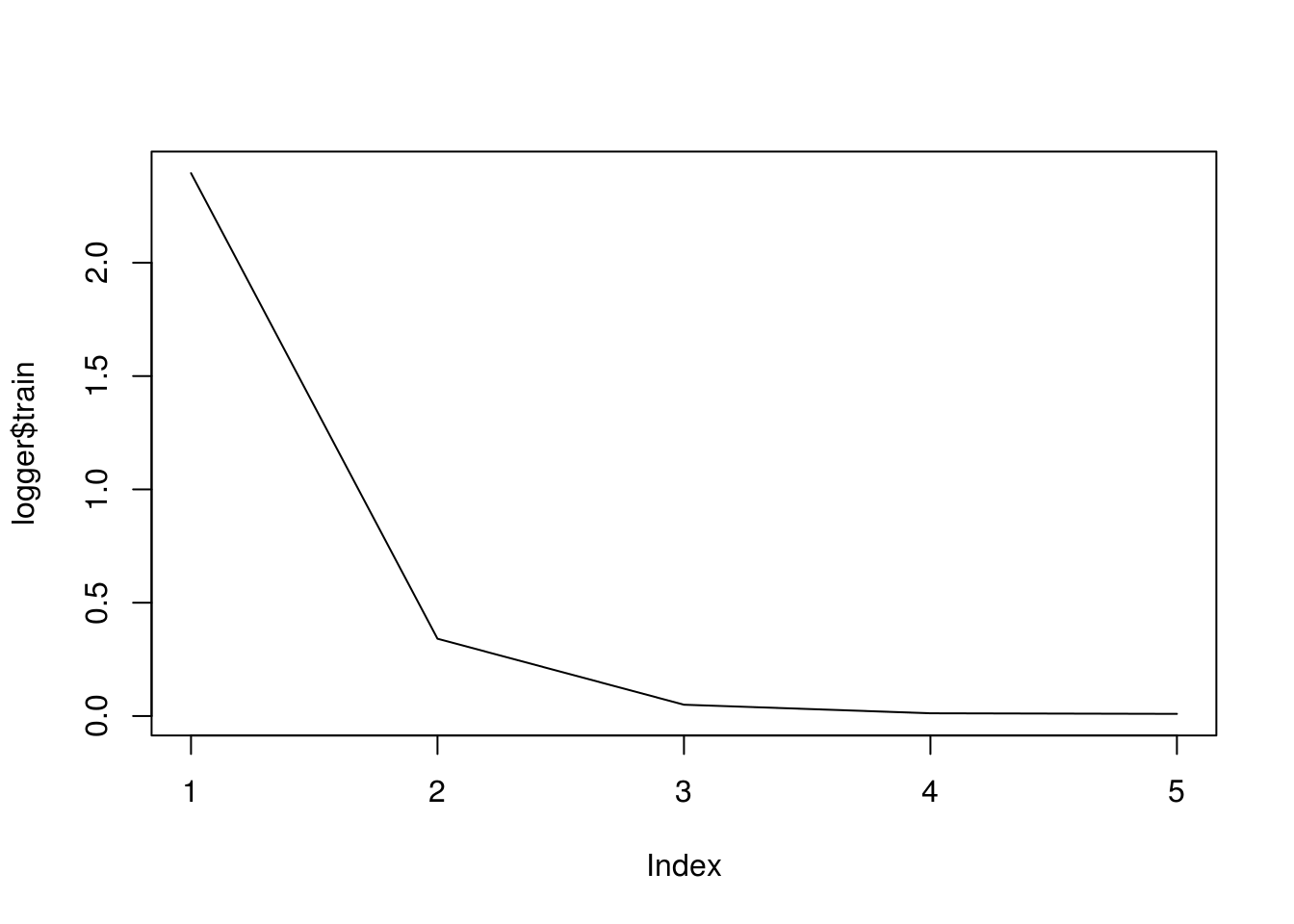
Проверим, как работает наша модель:

predict(model, t(X[1:5, ]))
y[1:5]

## Warning in mx.model.select.layout.predict(X, model): Auto detect layout input matrix, use colmajor..

##           [,1]     [,2]     [,3]     [,4]     [,5]
## [1,] 0.3129134 4.070303 4.975691 8.280487 8.931004

y[1:5]

## [1] 0.3211988 4.0561930 4.9810253 8.2959409 8.9414367

Все работает, можно переходить к более серьезному примеру!

10. Решение задачи регрессии на реальных данных

Рассмотрим решение задачи регрессии на примере прогнозирования степени проникаемости (по сути — скорости пассивной диффузии) вещества через монослой клеток исходя из известных свойств этого вещества (подробнее см. здесь).

Описанной задаче посвящена работа ADME evaluation in drug discovery. 5. Correlation of Caco-2 permeation with simple molecular properties. В ней приводится таблица, содержащая характеристики 77 различных по структуре веществ, а также экспериментальные данные по проникаемости этих веществ. Следует отметить, что данные, полученные для одного и того же вещества в ходе разных экспериментов, могут значительно варьировать. Но мы не будем углубляться в этот аспект проблемы, а просто возьмем те данные, с которыми работали авторы публикации.

Загрузим данные при помощи кода, созданного полезной функцией dump():

# df <- read_excel("caco2.xlsx")
# dump("df", stdout())

df <-
structure(list(name = c("acebutolol", "acebutolol_ester", "acetylsalic_acid", 
"acyclovir", "alprenolol", "alprenolol ester", "aminopyrin", 
"artemisinin", "artesunate", "atenolol", "betazolol ester", "betazolol_", 
"bremazocine", "caffeine", "chloramphenicol", "chlorothiazide", 
"chlorpromazine", "cimetidine", "clonidine", "corticosterone", 
"desiprarnine", "dexamethas", "dexamethas_beta_D_glucoside", 
"dexamethas_beta_D_glucuronide", "diazepam", "dopamine", "doxorubici", 
"erythromycin", "estradiol", "felodipine", "ganciclovir", "griseofulvin", 
"hydrochlorothiazide", "hydrocortisone", "ibuprophen", "imipramine", 
"indomethacin", "labetalol", "mannitol", "meloxicam", "methanol", 
"methotrexate", "methylscopolamine", "metoprolol", "nadolol", 
"naproxen", "nevirapine", "nicotine", "olsalazine", "oxprenolol", 
"oxprenolol ester", "phencyclidine", "Phenytoin", "pindolol", 
"pirenzepine", "piroxicam", "pnu200603", "practolol", "prazocin", 
"progesterone", "propranolol", "propranolo_ester", "quinidine", 
"ranitidine", "salicylic acid", "scopolamine", "sucrose", "sulfasalazine", 
"telmisartan", "terbutaline", "tesosterone", "timolol", "timolol_ester", 
"uracil", "urea", "warfarine", "zidovudine"), log_P_eff_exp = c(-5.83, 
-4.61, -5.06, -6.15, -4.62, -4.47, -4.44, -4.52, -5.4, -6.44, 
-4.81, -4.52, -5.1, -4.41, -4.69, -6.72, -4.7, -5.89, -4.59, 
-4.47, -4.67, -4.75, -6.54, -6.12, -4.32, -5.03, -6.8, -5.43, 
-4.77, -4.64, -6.27, -4.44, -6.06, -4.66, -4.28, -4.85, -4.69, 
-5.03, -6.21, -4.71, -4.58, -5.92, -6.16, -4.59, -5.41, -4.83, 
-4.52, -4.71, -6.96, -4.68, -4.51, -4.61, -4.57, -4.78, -6.36, 
-4.45, -6.25, -6.05, -4.36, -4.37, -4.58, -4.48, -4.69, -6.31, 
-4.79, -4.93, -5.77, -6.33, -4.82, -6.38, -4.34, -4.85, -4.6, 
-5.37, -5.34, -4.68, -5.16), log_D = c(-0.09, 1.59, -2.25, -1.8, 
1.38, 2.78, 0.63, 2.22, -0.88, -1.81, 0.28, 0.63, 1.66, 0.02, 
1.14, -1.15, 1.86, -0.36, 0.78, 1.78, 1.57, 1.89, 0.58, -1.59, 
2.58, -0.8, -0.16, 1.26, 2.24, 3.48, -0.87, 2.47, -0.12, 1.48, 
0.68, 2.52, 1, 1.24, -2.65, 0.03, -0.7, -2.53, -1.14, 0.51, 0.68, 
0.42, 1.81, 0.41, -4.5, 0.45, 1.98, 1.31, 2.26, 0.19, -0.46, 
-0.07, -4, -1.4, 1.88, 3.48, 1.55, 3.02, 2.04, -0.12, -1.44, 
0.21, -3.34, -0.42, 2.41, -1.07, 3.11, 0.03, 1.74, -1.11, -1.64, 
0.64, -0.58), rgyr = c(4.64, 5.12, 3.41, 3.37, 3.68, 3.84, 2.97, 
2.75, 4.02, 4.58, 5.41, 5.64, 3.43, 2.47, 3.75, 3.11, 3.74, 4.26, 
2.79, 3.68, 3.4, 3.6, 5.67, 5.75, 3.28, 2.67, 4.85, 4.99, 3.44, 
3.39, 3.7, 3.37, 3.11, 3.72, 3.45, 3.44, 4.16, 4.61, 2.48, 3.34, 
0.84, 5.33, 3.67, 4.59, 4.37, 3.38, 2.94, 2.5, 4.62, 3.63, 3.87, 
2.91, 2.97, 3.71, 3.55, 3.17, 3.89, 4.02, 4.96, 3.58, 3.63, 4.13, 
3.25, 5.13, 2.14, 3.63, 3.49, 5.68, 5.29, 3.15, 3.33, 4.02, 3.98, 
1.84, 1.23, 3.45, 3.14), rgyr_d = c(4.51, 5.03, 3.24, 3.23, 3.69, 
3.88, 2.97, 2.75, 3.62, 4.52, 5.27, 5.39, 3.38, 2.47, 3.73, 3.11, 
3.69, 4.24, 2.79, 3.71, 3.42, 3.66, 5.28, 5.23, 3.28, 2.68, 4.9, 
5.01, 3.44, 3.48, 3.48, 3.37, 3.11, 3.79, 3.36, 3.45, 3.16, 4.46, 
2.59, 3.36, 0.84, 5.18, 3.74, 4.53, 4.1, 3.43, 2.94, 2.5, 4.37, 
3.56, 3.9, 2.91, 2.97, 3.71, 3.4, 3.26, 3.79, 4.09, 4.99, 3.62, 
3.53, 4.06, 3.3, 4.57, 2.14, 3.49, 3.54, 5.53, 5.01, 3.15, 3.33, 
4.01, 4.13, 1.84, 1.23, 3.5, 3.13), HCPSA = c(82.88, 77.08, 79.38, 
120.63, 38.92, 35.53, 20.81, 54.27, 102.05, 86.82, 43.02, 47.14, 
49.56, 45.55, 113.73, 138.76, 4.6, 105.44, 30.03, 75.95, 13.8, 
90.74, 163.95, 186.88, 25.93, 75.13, 186.78, 138.69, 44.34, 50.34, 
139.45, 67.55, 142.85, 93.37, 39.86, 3.56, 67.13, 93.29, 127.46, 
93.21, 25.64, 204.96, 51.29, 44.88, 86.73, 76.98, 36.68, 15.1, 
144.08, 48.62, 49.58, 1.49, 65.63, 52.8, 59.71, 99.19, 69.89, 
64.79, 86.76, 38.1, 40.42, 36.21, 43.77, 105.15, 61.71, 57.35, 
187.69, 133.67, 55.48, 79.52, 42.35, 100.74, 96.25, 66.72, 82.72, 
59.47, 96.33), TPSA = c(87.66, 93.73, 89.9, 114.76, 41.49, 47.56, 
26.79, 53.99, 100.52, 84.58, 50.72, 56.79, 43.7, 58.44, 115.38, 
118.69, 6.48, 88.89, 36.42, 74.6, 15.27, 94.83, 173.98, 191.05, 
32.67, 66.48, 206.07, 193.91, 40.46, 64.63, 134.99, 71.06, 118.36, 
94.83, 37.3, 6.48, 68.53, 95.58, 121.38, 99.6, 20.23, 210.54, 
59.06, 50.72, 81.95, 46.53, 58.12, 16.13, 139.78, 50.72, 56.79, 
3.24, 58.2, 57.28, 68.78, 99.6, 91.44, 70.59, 106.95, 34.14, 
41.49, 47.56, 45.59, 86.26, 57.53, 62.3, 189.53, 141.31, 72.94, 
72.72, 37.3, 79.74, 85.81, 58.2, 69.11, 63.6, 103.59), N_rotb = c(0.31, 
0.29, 0.23, 0.21, 0.29, 0.27, 0.17, 0.07, 0.16, 0.29, 0.27, 0.26, 
0.15, 0.12, 0.28, 0.08, 0.14, 0.33, 0.08, 0.1, 0.11, 0.13, 0.17, 
0.17, 0.06, 0.23, 0.18, 0.21, 0.06, 0.22, 0.25, 0.16, 0.08, 0.12, 
0.24, 0.13, 0.19, 0.24, 0.44, 0.16, 0.2, 0.26, 0.16, 0.3, 0.24, 
0.19, 0.05, 0.07, 0.27, 0.31, 0.29, 0.04, 0.06, 0.23, 0.08, 0.13, 
0.15, 0.29, 0.15, 0.07, 0.22, 0.22, 0.14, 0.33, 0.19, 0.15, 0.28, 
0.2, 0.15, 0.29, 0.06, 0.24, 0.23, 0, 0.29, 0.15, 0.18), log_P_eff_calc = c(-5.3, 
-4.89, -5.77, -5.91, -4.58, -4.39, -4.63, -4.47, -5.64, -5.85, 
-5.2, -5.13, -4.57, -4.89, -5.11, -5.87, -4.38, -5.55, -4.69, 
-4.78, -4.46, -4.77, -5.83, -6.55, -4.45, -5.27, -6, -5.13, -4.57, 
-4.44, -5.79, -4.59, -5.62, -4.94, -4.78, -4.28, -5, -5.09, -5.87, 
-5.27, -4.67, -6.79, -5.37, -4.99, -5.15, -5.09, -4.49, -4.65, 
-6.97, -4.84, -4.45, -4.42, -4.6, -5.02, -5.3, -5.31, -6.37, 
-5.5, -5.05, -4.54, -4.57, -4.5, -4.46, -5.6, -5.29, -5.07, -6.56, 
-6.06, -4.85, -5.36, -4.53, -5.35, -4.82, -5.23, -5.29, -4.95, 
-5.43), residuals = c(-0.53, 0.28, 0.71, -0.24, -0.04, -0.08, 
0.19, -0.05, 0.24, -0.59, 0.39, 0.61, -0.53, 0.48, 0.42, -0.85, 
-0.32, -0.34, 0.1, 0.31, -0.21, 0.02, -0.71, 0.43, 0.13, 0.24, 
-0.8, -0.3, -0.2, -0.2, -0.48, 0.15, -0.44, 0.28, 0.5, -0.57, 
0.31, 0.06, -0.34, 0.56, 0.09, 0.87, -0.79, 0.4, -0.26, 0.26, 
-0.03, -0.06, 0.01, 0.16, -0.06, -0.19, 0.03, 0.24, -1.06, 0.86, 
0.12, -0.55, 0.69, 0.17, -0.01, 0.02, -0.23, -0.71, 0.5, 0.14, 
0.79, -0.27, 0.03, -1.02, 0.19, 0.5, 0.22, -0.14, -0.05, 0.27, 
0.27)), row.names = c(NA, -77L), class = c("tbl_df", "tbl", "data.frame"
))

Целевой переменной является log_P_eff_exp — логарифм скорости диффузии (которая измеряется в см/с).

Список предикторов:

• log_D — коэффициент распределения при pH = 7.4;
• rgyr — радиус гирации;
• rgyr_d — динамический радиус гирации;
• HCPSA — площадь сильно заряженной полярной поверхности;
• TPSA — топологическая площать полярной поверхности;
• N_rotb — число поворотных связей.

Рассмотрим распределения предикторов, а также их парные корреляции:

GGally::ggpairs(df, 
                columns = c(3:8),
                diag = list(continuous = "barDiag"))

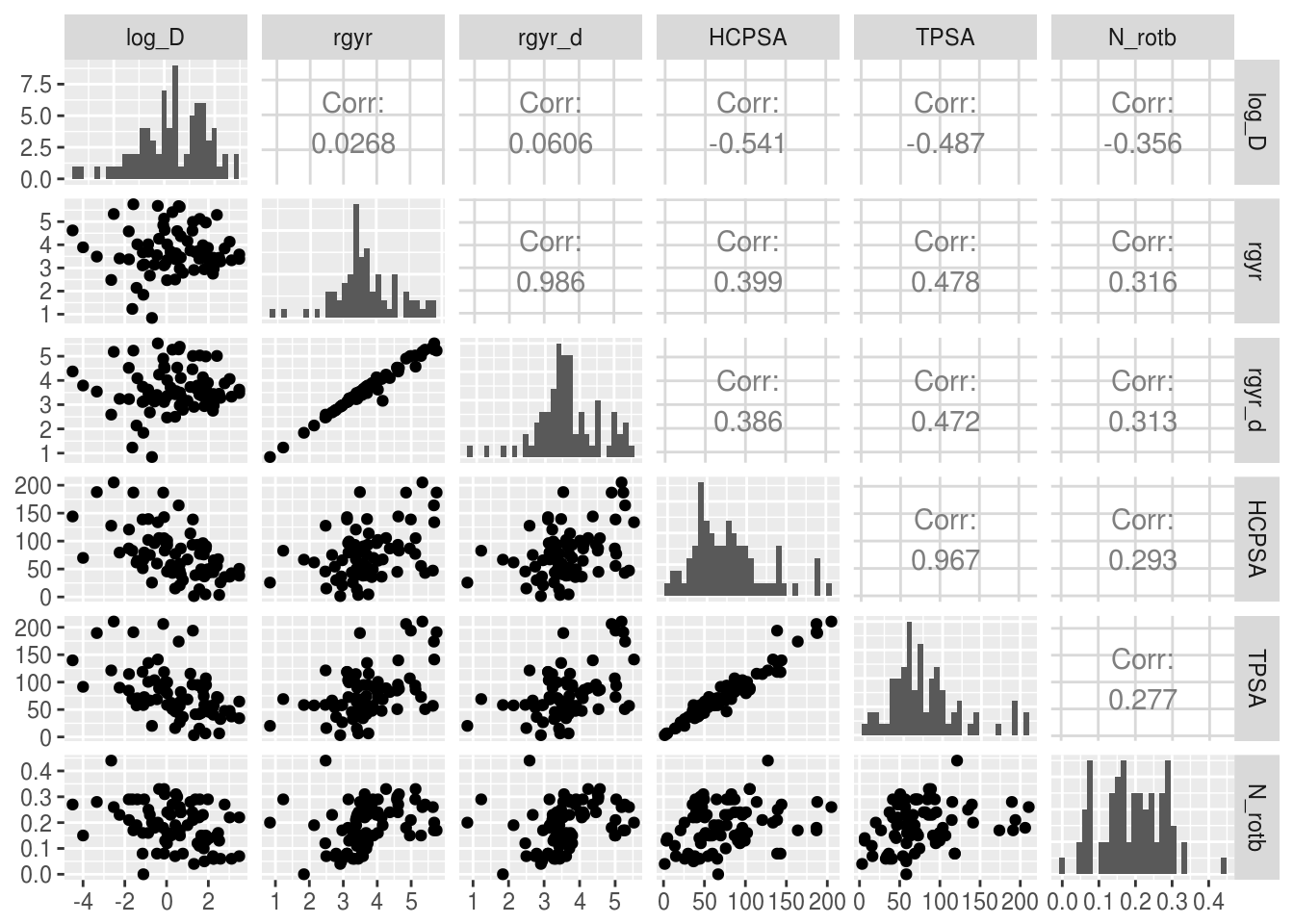
Переменные rgyr и rgyr_d, а также HCPSA и TPSA предсказуемо сильно коррелируют, поскольку в обоих случаях пары переменных представляют собой разные способы расчета одной и той же физической величины.

Обучим такую же нейронную сеть, как и в предыдущем примере. На этот раз разобъем выборку на обучающую и проверочную, и в этот раз обойдемся без итераторов.

set.seed(42)
train_ind <- sample(1:77, 60)
x_train <- as.matrix(df[train_ind, 2:8])
y_train <- unlist(df[train_ind, 9])
x_val <- as.matrix(df[-train_ind, 2:8])
y_val <- unlist(df[-train_ind, 9])

data <- mx.symbol.Variable("data")
fc1 <- mx.symbol.FullyConnected(data, 
                                num_hidden = 1)
linreg <- mx.symbol.LinearRegressionOutput(fc1)

initializer <- mx.init.normal(sd = 0.1)

optimizer <- mx.opt.create("sgd", 
                           learning.rate = 1e-6,
                           momentum = 0.9)

logger <- mx.metric.logger()
epoch.end.callback <- mx.callback.log.train.metric(
    period = 4, # число батчей, после которого оценивается метрика
    logger = logger)

n_epoch <- 20

model <- mx.model.FeedForward.create(
    symbol = linreg, 
    X = x_train, 
    y = y_train,
    ctx = mx.cpu(), 
    num.round = n_epoch, 
    initializer = initializer, 
    optimizer = optimizer,
    eval.data = list(data = x_val, label = y_val),
    eval.metric = mx.metric.rmse,
    array.batch.size = 15,
    epoch.end.callback = epoch.end.callback)

Посмотрим, как менялась метрика RMSE на обучающей и проверочной выборке:

rmse_log <- data.frame(RMSE = c(logger$train, logger$eval),
                       dataset = c(rep("train", 
                                       length(logger$train)), 
                                   rep("val", 
                                       length(logger$eval))),
                       epoch = 1:n_epoch)

library(ggplot2)

ggplot(rmse_log, aes(epoch, RMSE, 
                     group = dataset,
                     colour = dataset)) +
  geom_point() +
  geom_line()

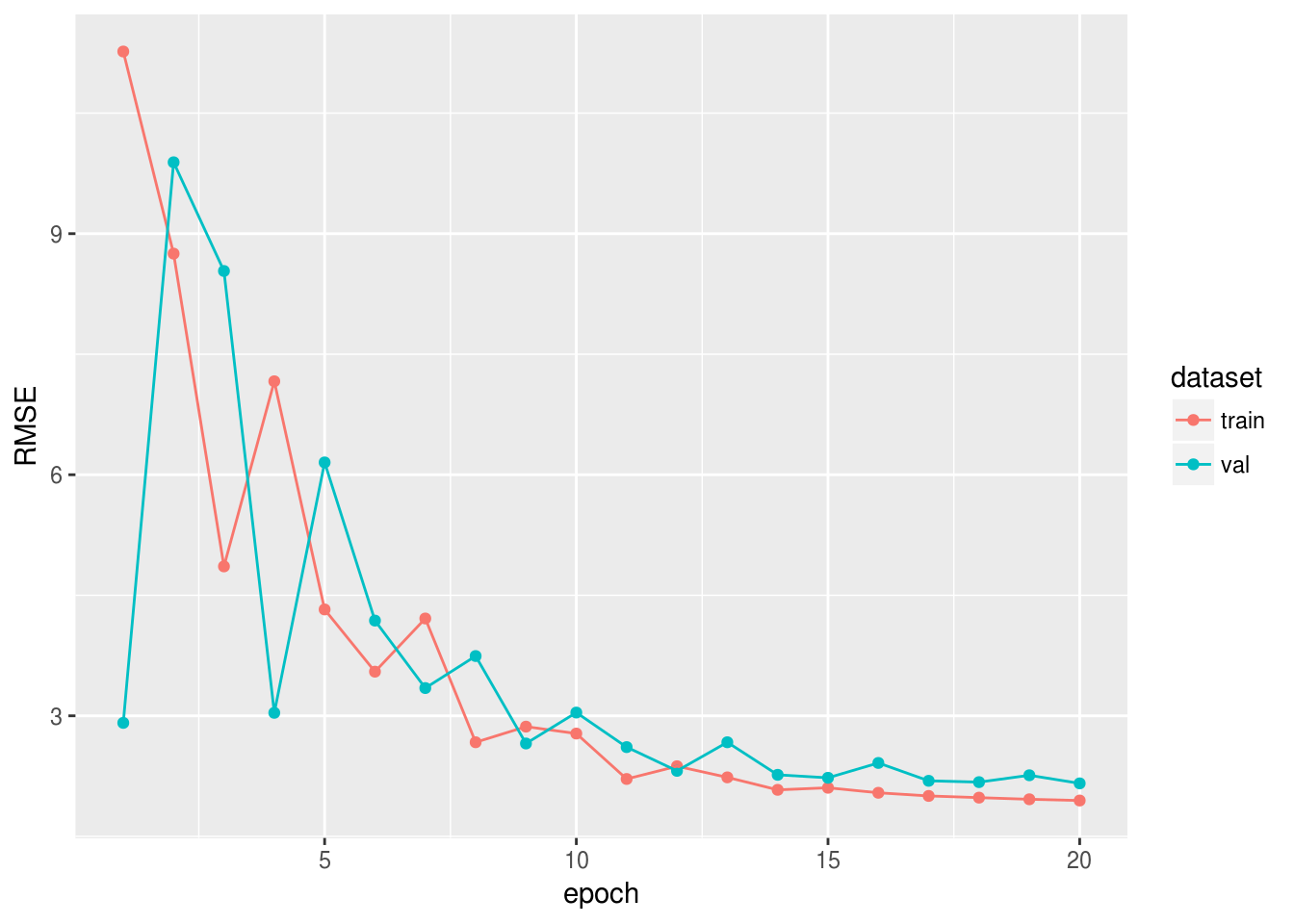
В следующем сообщении мы решим задачу классификации на реальных данных, а также рассмотрим другие метрики качества и использование ранней остановки.

Автор: Андрей Огурцов

Источник