Введение
В предыдущей статье цикла мы обсудили постановку задачи анализа данных, сделали первые шаги в настройке модели машинного обучения и написали интерфейс, удобный для использования прикладным программистом. Сегодня мы проведем дальнейшее исследование задачи — поэкспериментируем с новыми фичами, попробуем более сложные модели и варианты их настроечных параметров.
В статье, насколько возможно, используется русскоязычная терминология, выбранная автором на основе буквальных переводов англоязычных терминов и устоявшегося в сообществе сленга. О ней можно почитать здесь.
Вспомним, на чем мы остановились в плане настройки модели и оценки качества ее предсказания на валидационной выборке.
[research.py]
import pickle
import math
import numpy
from sklearn.linear_model import LinearRegression
TRAIN_SAMPLES_NUM = 20000
def load_data():
list_of_instances = []
list_of_labels =[]
with open('./data/competition_data/train_set.csv') as input_stream:
header_line = input_stream.readline()
columns = header_line.strip().split(',')
for line in input_stream:
new_instance = dict(zip(columns[:-1], line.split(',')[:-1]))
new_label = float(line.split(',')[-1])
list_of_instances.append(new_instance)
list_of_labels.append(new_label)
return list_of_instances, list_of_labels
def is_bracket_pricing(instance):
if instance['bracket_pricing'] == 'Yes':
return [1]
elif instance['bracket_pricing'] == 'No':
return [0]
else:
raise ValueError
def get_quantity(instance):
return [int(instance['quantity'])]
def get_min_order_quantity(instance):
return [int(instance['min_order_quantity'])]
def get_annual_usage(instance):
return [int(instance['annual_usage'])]
def get_absolute_date(instance):
return [365 * int(instance['quote_date'].split('-')[0])
+ 12 * int(instance['quote_date'].split('-')[1])
+ int(instance['quote_date'].split('-')[2])]
SUPPLIERS_LIST = ['S-0058', 'S-0013', 'S-0050', 'S-0011', 'S-0070', 'S-0104', 'S-0012', 'S-0068', 'S-0041', 'S-0023', 'S-0092', 'S-0095', 'S-0029', 'S-0051', 'S-0111', 'S-0064', 'S-0005', 'S-0096', 'S-0062', 'S-0004', 'S-0059', 'S-0031', 'S-0078', 'S-0106', 'S-0060', 'S-0090', 'S-0072', 'S-0105', 'S-0087', 'S-0080', 'S-0061', 'S-0108', 'S-0042', 'S-0027', 'S-0074', 'S-0081', 'S-0025', 'S-0024', 'S-0030', 'S-0022', 'S-0014', 'S-0054', 'S-0015', 'S-0008', 'S-0007', 'S-0009', 'S-0056', 'S-0026', 'S-0107', 'S-0066', 'S-0018', 'S-0109', 'S-0043', 'S-0046', 'S-0003', 'S-0006', 'S-0097']
def get_supplier(instance):
if instance['supplier'] in SUPPLIERS_LIST:
supplier_index = SUPPLIERS_LIST.index(instance['supplier'])
result = [0] * supplier_index + [1] + [0] * (len(SUPPLIERS_LIST) - supplier_index - 1)
else:
result = [0] * len(SUPPLIERS_LIST)
return result
def get_assembly(instance):
assembly_id = int(instance['tube_assembly_id'].split('-')[1])
result = [0] * assembly_id + [1] + [0] * (25000 - assembly_id - 1)
return result
def get_assembly_specs(instance, assembly_to_specs):
result = [0] * 100
for spec in assembly_to_specs[instance['tube_assembly_id']]:
result[int(spec.split('-')[1])] = 1
return result
def to_sample(instance, additional_data):
return (is_bracket_pricing(instance) + get_quantity(instance) + get_min_order_quantity(instance)
+ get_annual_usage(instance) + get_absolute_date(instance) + get_supplier(instance)
+ get_assembly_specs(instance, additional_data['assembly_to_specs']))
def to_interim_label(label):
return math.log(label + 1)
def to_final_label(interim_label):
return math.exp(interim_label) - 1
def load_additional_data():
result = dict()
assembly_to_specs = dict()
with open('data/competition_data/specs.csv') as input_stream:
header_line = input_stream.readline()
for line in input_stream:
tube_assembly_id = line.split(',')[0]
specs = []
for spec in line.strip().split(',')[1:]:
if spec != 'NA':
specs.append(spec)
assembly_to_specs[tube_assembly_id] = specs
result['assembly_to_specs'] = assembly_to_specs
return result
if __name__ == '__main__':
list_of_instances, list_of_labels = load_data()
print(len(list_of_instances), len(list_of_labels))
print(list_of_instances[:3])
print(list_of_labels[:3])
# print(list(map(to_sample, list_of_instances[:3])))
additional_data = load_additional_data()
# print(additional_data)
print(to_final_label(to_interim_label(42)))
model = LinearRegression()
list_of_samples = list(map(lambda x:to_sample(x, additional_data), list_of_instances))
train_samples = list_of_samples[:TRAIN_SAMPLES_NUM]
train_labels = list(map(to_interim_label, list_of_labels[:TRAIN_SAMPLES_NUM]))
model.fit(train_samples, train_labels)
validation_samples = list_of_samples[TRAIN_SAMPLES_NUM:]
validation_labels = list(map(to_interim_label, list_of_labels[TRAIN_SAMPLES_NUM:]))
squared_errors = []
for sample, label in zip(validation_samples, validation_labels):
prediction = model.predict(numpy.array(sample).reshape(1, -1))[0]
squared_errors.append((prediction - label) ** 2)
mean_squared_error = math.sqrt(sum(squared_errors) / len(squared_errors))
print('Mean Squared Error: {0}'.format(mean_squared_error))
with open('./data/model.mdl', 'wb') as output_stream:
output_stream.write(pickle.dumps(model))
[generate_response.py]
import pickle
import numpy
import research
class FinalModel(object):
def __init__(self, model, to_sample, additional_data):
self._model = model
self._to_sample = to_sample
self._additional_data = additional_data
def process(self, instance):
return self._model.predict(numpy.array(self._to_sample(
instance, self._additional_data)).reshape(1, -1))[0]
if __name__ == '__main__':
with open('./data/model.mdl', 'rb') as input_stream:
model = pickle.loads(input_stream.read())
additional_data = research.load_additional_data()
final_model = FinalModel(model, research.to_sample, additional_data)
print(final_model.process({'tube_assembly_id':'TA-00001', 'supplier':'S-0066',
'quote_date':'2013-06-23', 'annual_usage':'0',
'min_order_quantity':'0', 'bracket_pricing':'Yes',
'quantity':'1'}))
Было подобрано несколько фичей, описывающих объекты, на которых мы обучаем наш алгоритм (а это, напомню, такая скучная и, казалось бы, далекая от ИТ вещь как промышленные трубы). На основе этих фичей работает ключевая функция to_sample(), которая в настоящий момент выглядит следующим образом:
def to_sample(instance, additional_data):
return (is_bracket_pricing(instance) + get_quantity(instance)
+ get_min_order_quantity(instance) + get_annual_usage(instance)
+ get_absolute_date(instance) + get_supplier(instance)
+ get_assembly_specs(instance, additional_data['assembly_to_specs']))
На вход она берет описание объекта (переменная instance), содержащееся в основном файле train_set.csv и набор дополнительных данных, сгенерированных на основе остальных файлов из датасета, а на выходе возвращает массив фиксированной длины, в дальнейшем подающийся на вход алгоритму машинного обучения.
Касательно конкретно моделирования никакого особенного прогресса пока не произошло — все еще используется элементарная линейная регрессия без каких бы то ни было настроек, отличающихся от заданных по умолчанию пакетом Scikit-Learn. Тем не менее, пока что продолжим постепенно увеличивать список фичей для улучшения качества предсказания алгоритма. Прошлый раз мы уже (весьма, правда, банальным образом) использовали все колонки основного файла с тренировочными данными train_set.csv и файл с вспомогательными данными specs.csv. Так что теперь, пожалуй, настало время обратить внимание на остальные файлы с дополнительными данными. В частности, перспективно выглядит содержание файла bill_of_materials.csv, описывающее компоненты каждого из изделий.
Дальнейший фичеселект
$ head ./data/competition_data/bill_of_materials.csv
tube_assembly_id,component_id_1,quantity_1,component_id_2,quantity_2,component_id_3,quantity_3,component_id_4,quantity_4,component_id_5,quantity_5,component_id_6,quantity_6,component_id_7,quantity_7,component_id_8,quantity_8
TA-00001,C-1622,2,C-1629,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00002,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00003,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00004,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00005,C-1624,1,C-1631,1,C-1641,1,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00006,C-1624,1,C-1631,1,C-1641,1,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00007,C-1622,2,C-1629,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00008,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
TA-00009,C-1625,2,C-1632,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
Как видим, формат файла напоминает specs.csv. Для начала посмотрим, сколько фактически встречается видов компонент и уже с помощью этой информации примем решение о том, какую фичу разумно сформировать на основе этих вспомогательных данных.
>>> set_of_components = set()
>>> with open('./data/competition_data/bill_of_materials.csv') as input_stream:
... header_line = input_stream.readline()
... for line in input_stream:
... for i in range(1, 16, 2):
... new_component = line.split(',')[i]
... set_of_components.add(new_component)
...
>>> len(set_of_components)
2049
>>> sorted(set_of_components)[:10]
['9999', 'C-0001', 'C-0002', 'C-0003', 'C-0004', 'C-0005', 'C-0006', 'C-0007', 'C-0008', 'C-0009']
Компонент оказалось немало, так что идея стандартным образом разворачивать фичу в массив из более чем 2000 элементов не кажется очень разумной. Попробуем использовать несколько десятков самых популярных вариантов, а также оставить переменную, отвечающую за количество этих варинтов в качестве настроечного параметра для оптимизации на стадии тонкой настройки.
def load_additional_data():
result = dict()
...
assembly_to_components = dict()
component_to_popularity = dict()
with open('./data/competition_data/bill_of_materials.csv') as input_stream:
header_line = input_stream.readline()
for line in input_stream:
tube_assembly_id = line.split(',')[0]
assembly_to_components[tube_assembly_id] = dict()
for i in range(1, 16, 2):
new_component = line.split(',')[i]
if new_component != 'NA':
quantity = int(line.split(',')[i + 1])
assembly_to_components[tube_assembly_id][new_component] = quantity
if new_component in component_to_popularity:
component_to_popularity[new_component] += 1
else:
component_to_popularity[new_component] = 1
components_by_popularity = [value[0] for value in sorted(
component_to_popularity.items(),
key=operator.itemgetter(1, 0), reverse=True)]
result['assembly_to_components'] = assembly_to_components
result['components_by_popularity'] = components_by_popularity
...
def get_assembly_components(instance, assembly_to_components,
components_by_popularity, number_of_components):
"""
number_of_components: number of most popular components taken into account
"""
result = [0] * number_of_components
for component in sorted(assembly_to_components[instance['tube_assembly_id']]):
component_index = components_by_popularity.index(component)
if component_index < number_of_components:
# quantity
result[component_index] = assembly_to_components[
instance['tube_assembly_id']][component]
return result
def to_sample(instance, additional_data):
return (is_bracket_pricing(instance) + get_quantity(instance)
+ get_min_order_quantity(instance) + get_annual_usage(instance)
+ get_absolute_date(instance) + get_supplier(instance)
+ get_assembly_specs(instance, additional_data['assembly_to_specs'])
+ get_assembly_components(instance,
additional_data['assembly_to_components'],
additional_data['components_by_popularity'], 100)
)
Запустим программу без новой фичи чтобы вспомнить, каков был результат на валидации.
Mean Squared Error: 0.7754770419953809
А теперь добавим новую фичу.
Mean Squared Error: 0.711158610883329
Как видим, качество предсказания опять значительно возросло. Кстати у нас появился первый численный настроечный параметр, а именно — количество наиболее популярных компонент, которые мы учитываем. Попробуем его поварьировать, имея ввиду, что, исходя из общих соображений, при увеличении параметра качество предсказания должно улучшаться — ведь мы учитываем все больше и больше неиспользованной ранее информации.
100: 0.711158610883329
200: 16433833.592963027
150: 0.7110152873760721
170: 19183113.422557358
160: 0.7107685953594116
165: 0.7119011633609398
168: 24813512.02303443
166: 0.7119603793730067
167: 0.7119604617354474
Пока трудно сказать, что за катастрофа происходит при превышении значения 168, по какой причине качество предсказания так резко и внезапно ухудшается. В остальном — мы не видим сколько-нибудь значительных изменений. Для очистки совести посмотрим, как будет изменяться качество предсказания при уменьшении варьируемого параметра.
80: 0.7116311373463766
50: 0.7211560841347712
30: 0.7548570148032887
70: 0.7121518708790175
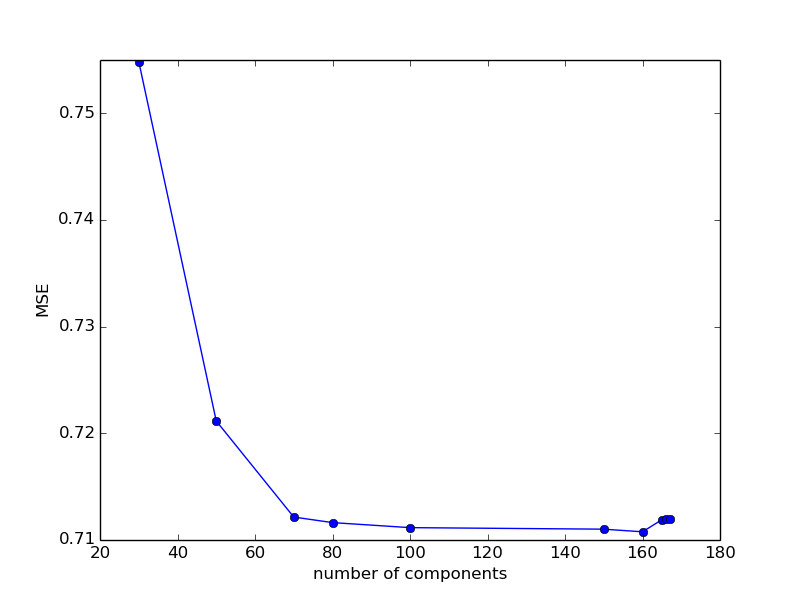
Видно, что при уменьшении количества компонент ошибка увеличивается, а при значениях между 80 и 160 остается приблизительно постоянной. Оставим пока что параметр равным 100.
Как видим, добавление новых фич все еще дает значительные улучшения на валидации. Проведем еще парочку экспериментов такого рода и после этого перейдем к варьированию моделей обучения и их настроечных параметров. Рассмотрим более сложно устроенный, но, судя по описанию файлов с данными, ключевой, файл tube.csv.
$ head data/competition_data/tube.csv
tube_assembly_id,material_id,diameter,wall,length,num_bends,bend_radius,end_a_1x,end_a_2x,end_x_1x,end_x_2x,end_a,end_x,num_boss,num_bracket,other
TA-00001,SP-0035,12.7,1.65,164,5,38.1,N,N,N,N,EF-003,EF-003,0,0,0
TA-00002,SP-0019,6.35,0.71,137,8,19.05,N,N,N,N,EF-008,EF-008,0,0,0
TA-00003,SP-0019,6.35,0.71,127,7,19.05,N,N,N,N,EF-008,EF-008,0,0,0
TA-00004,SP-0019,6.35,0.71,137,9,19.05,N,N,N,N,EF-008,EF-008,0,0,0
TA-00005,SP-0029,19.05,1.24,109,4,50.8,N,N,N,N,EF-003,EF-003,0,0,0
TA-00006,SP-0029,19.05,1.24,79,4,50.8,N,N,N,N,EF-003,EF-003,0,0,0
TA-00007,SP-0035,12.7,1.65,202,5,38.1,N,N,N,N,EF-003,EF-003,0,0,0
TA-00008,SP-0039,6.35,0.71,174,6,19.05,N,N,N,N,EF-008,EF-008,0,0,0
TA-00009,SP-0029,25.4,1.65,135,4,63.5,N,N,N,N,EF-003,EF-003,0,0,0
Заметим, что содержимое колонки «material_id» совпадает по префиксу с значениями, указанными в specs.csv. Что это значит сказать пока трудно, да и проведя поиск нескольких значений вида SP-xyzt, содержащихся в первых 20 строках specs.csv мы ничего не найдем, но стоит на всякий случай запомнить эту особенность. Также, исходя из описания соревнования, трудно понять фактическую разницу между материалом, указанным в колонке и материалами, указанными в bill_of_materials.csv. Не будем, однако, пока что терзать себя столь мудреными вопросами и попробуем уже привычным образом проанализировать количество возможных вариантов и сконвертировать значение в (будем надеяться) полезную для алгоритма фичу.
>>> set_of_materials = set()
>>> with open('./data/competition_data/tube.csv') as input_stream:
... header_line = input_stream.readline()
... for line in input_stream:
... new_material = line.split(',')[1]
... set_of_materials.add(new_material)
...
>>> len(set_of_materials)
20
>>> set_of_materials
{'SP-0034', 'SP-0037', 'SP-0039', 'SP-0030', 'SP-0029', 'NA', 'SP-0046', 'SP-0028', 'SP-0031', 'SP-0032', 'SP-0033', 'SP-0019', 'SP-0048', 'SP-0008', 'SP-0045', 'SP-0035', 'SP-0044', 'SP-0036', 'SP-0041', 'SP-0038'}
Получилось вполне обозримое количество вариантов, так что мы можем не особенно задумываясь добавить стандартный категориальный признак. Для этого сперва дополним функцию load_additional_data() подгрузкой словаря assembly_to_material.
assembly_to_material = dict()
with open('./data/competition_data/tube.csv') as input_stream:
header_line = input_stream.readline()
for line in input_stream:
tube_assembly_id = line.split(',')[0]
material_id = line.split(',')[1]
assembly_to_material[tube_assembly_id] = material_id
result['assembly_to_material'] = assembly_to_material
И используем его при написании похожей на одну из уже имеющихся функций.
MATERIALS_LIST = ['NA', 'SP-0008', 'SP-0019', 'SP-0028', 'SP-0029', 'SP-0030', 'SP-0031', 'SP-0032', 'SP-0033', 'SP-0034', 'SP-0035', 'SP-0036', 'SP-0037', 'SP-0038', 'SP-0039', 'SP-0041', 'SP-0044', 'SP-0045', 'SP-0046', 'SP-0048']
def get_material(instance, assembly_to_material):
material = assembly_to_material[instance['tube_assembly_id']]
if material in MATERIALS_LIST:
material_index = MATERIALS_LIST.index(material)
result = [0] * material_index + [1] + [0] * (len(MATERIALS_LIST) - material_index - 1)
else:
result = [0] * len(MATERIALS_LIST)
return result
Mean Squared Error: 0.7187098083419174
Увы, данная фича не помогла нам улучшить уже имеющийся результат приблизительно равный 0.711. Но не беда — можно понадеяться, что наш труд все-таки не пропадет зря и поможет при настройке более сложной модели. Следующая колонка в том же файле tube.csv описывает диаметр трубы. Такое свойство объекта называется количественным и конвертируется в фичу самым простым и естественным способом, а именно — взятием значения. Конечно, в некоторых случаях может быть полезно так или иначе его отнормировать либо изменить каким-нибудь другим образом, но для первой попытки можно обойтись и без этого. Написав код, соответствующий этой фиче, ставшим уже привычным способом,
def get_diameter(instance, assembly_to_diameter):
return [assembly_to_diameter[instance['tube_assembly_id']]]
и добавив ее в функцию to_sample(), мы можем получить очередное улучшение качества предсказания модели на валидационной выборке.
Mean Squared Error: 0.6968043166687439
Как видим, простое извлечение новых и новых фичей и тестирование качества предсказания модели на валидационной выборке продолжает улучшать метрику качества. Однако, с одной стороны, прирост от новых фичей уже не так велик (а иногда и отрицателен — и тогда от соответствующей фичи приходится отказываться, как в предыдущем примере с материалом), а с другой — проект у нас учебный, а не соревновательный или рабочий, так что оставим на время подбор фичей и перейдем к вопросу выбора алгоритма и оптимизации параметров.
Варьируем модели
В рамках текущего набора признаков попробуем найти близкую к оптимальной модель машинного обучения и соответствующий ей набор гиперпараметров. Начнем с тестирования разных моделей. Попробуем для начала заменить простецкую линейную регрессию модной нейросеточкой из пакета Keras — одного из самых простых в использовании.
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
model = Sequential()
model.add(Dense(units=30, activation='tanh', input_dim=len(list_of_samples[0])))
model.add(Dense(units=1, activation='linear'))
optimizer = SGD(lr=0.1)
model.compile(loss='mean_squared_error', optimizer=optimizer, metrics=['accuracy'])
Что соответствуюет полносвязной архитектуре сети с количестов нейронов в слое равным 30, learning_rate равным 0.1 и активационной фукнцией tanh. Обратим внимание, что на выходном слое функция линейная, а не та или иная вариация сигмоиды, так как мы предсказываем численный параметр.
Mean Squared Error: nan
Ошибка оказалась настолько велика, что не поместилась в (весьма немаленький) numpy-евский int. Попробуем добавить еще один слой.
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
model = Sequential()
model.add(Dense(units=30, activation='tanh', input_dim=len(list_of_samples[0])))
model.add(Dense(units=20, activation='tanh', input_dim=len(list_of_samples[0])))
model.add(Dense(units=1, activation='linear'))
optimizer = SGD(lr=0.1)
model.compile(loss='mean_squared_error', optimizer=optimizer, metrics=['accuracy'])
Mean Squared Error: nan
Опять хорошего результата не получилось. Очень жаль, но, видимо, нейросети — модель полезная и хорошая, но не для нашей задачи. Впрочем, если кто-то умеет для нее получить хороший результат с помощью моделей нейросетевого типа, то жду ссылок на код в комментариях, а мы переключимся на более консервативные подходы. Например, одним из стандартных алгоритмов для решения задачи регрессии является градиентный бустинг. Давайте попробуем воспользоваться им.
model = GradientBoostingRegressor()
Mean Squared Error: 0.44000911792278125
Очевиден огромный прогресс, без сомнения поднявший нам настроения после оглушительного провала с разрекламированными нейросеточками. Тут, конечно, можно попробовать еще какой-нибудь алгоритм навроде RidgeRegression, но в общем-то автор и так знал, что градиентный бустинг для таких задач подходит хорошо, нейросети совсем плохо, а остальные модели — более-менее, так что не будем перебирать все возможные варианты, а займемся оптимизацией гиперпараметров наиболее подходящего из них, а именно бустинга.
Сходив на соответствующую страницу сайта посвященного библиотеке Scikit-Learn, расположенную тут или просто набрав в консоли help(GradientBoostingRegressor), мы узнаем, что у этой реализации алгоритма имеется следующий набор настроечных параметров и их значений по умолчанию:
loss=’ls’
learning_rate=0.1
n_estimators=100
subsample=1.0
criterion=’friedman_mse’
min_samples_split=2
min_samples_leaf=1
min_weight_fraction_leaf=0.0
max_depth=3
min_impurity_decrease=0.0
min_impurity_split=None
init=None
random_state=None
max_features=None
alpha=0.9
verbose=0
max_leaf_nodes=None
warm_start=False
presort=’auto’
Давайте разберем их один за одним и попробуем поизменять те из них, варьирование которых, на первый взгляд, может помочь улучшить качество предсказания.
| loss : {'ls', 'lad', 'huber', 'quantile'}, optional (default='ls')
| loss function to be optimized. 'ls' refers to least squares
| regression. 'lad' (least absolute deviation) is a highly robust
| loss function solely based on order information of the input
| variables. 'huber' is a combination of the two. 'quantile'
| allows quantile regression (use `alpha` to specify the quantile).
Функция потерь, которую мы оптимизируем. Казалось бы, после нашей переформулировки задачи (в части взятия логарифмов от меток и, соответственно, оптимизации MSE вместо LMSE) параметр по умолчанию соответствует нашей задаче. Оставляем как есть.
| learning_rate : float, optional (default=0.1)
| learning rate shrinks the contribution of each tree by `learning_rate`.
| There is a trade-off between learning_rate and n_estimators.
Во многих задачах ключевой для настройки параметр. Попробуем посмотреть, что будет при других значениях.
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.100}
...
model = GradientBoostingRegressor(learning_rate=MODEL_SETTINGS['learning_rate'])
Простая явная декларация гиперпараметра написана в такой, несколько вычурной, форме для того, чтобы в будущем было удобно менять параметры модели (и сами модели) в шапке скрипта, а также из соображений удобства логирования.
Mean Squared Error: 0.44002379237806705
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.200}
Mean Squared Error: 0.41423518862618164
Ага, при увеличении learning_rate метрика качества ощутимо улучшается. Попробуем продолжить изменять этот параметр в ту же сторону.
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.300}
Mean Squared Error: 0.4051555356961356
Увеличим еще
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.500}
Mean Squared Error: 0.39668129369369115
И еще
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':1.000}
Mean Squared Error: 0.434184026080522
При очередном увеличении параметра целевая метрика ухудшилась. Попробуем поискать что-то среди промежуточных значений.
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.700}
Mean Squared Error: 0.39998809063954305
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.600}
Mean Squared Error: 0.4032676539076024
Полученные в экспериментах данные уже довольно запутанные, давайте сведем их в таблицу и нарисуем соответствующий график (лично я глазами на графики в таких случаях обычно не смотрю, ограничиваясь мысленными построениями, однако для целей педагогического характера это может быть полезно).
| learning_rate | MSE |
|---|---|
| 0.100 | 0.4400 |
| 0.200 | 0.4142 |
| 0.300 | 0.4051 |
| 0.500 | 0.3966 |
| 0.600 | 0.4032 |
| 0.700 | 0.3999 |
| 1.000 | 0.4341 |
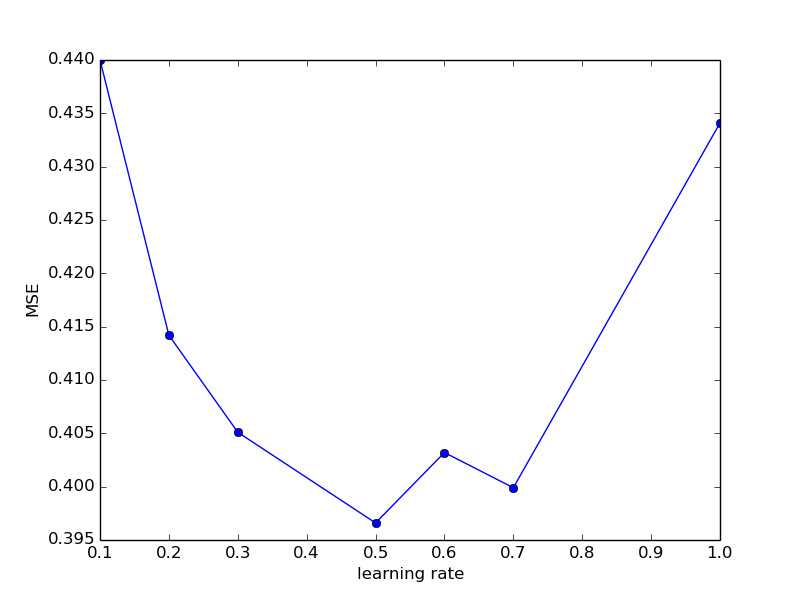
На первый взгляд выглядит так, как будто метрика качества при уменьшении learning_rate с 0.100 до 0.500 улучшается, потом, приблизительно до 0.700 остается относительно стабильной, а потом ухудшается. Проверим эту гипотезу еще большим количеством экспериментов.
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.400}
Mean Squared Error: 0.40129637223972486
MODEL_SETTINGS = {
'model_name': 'GradientBoostingRegressor',
'learning_rate': 0.800}
Mean Squared Error: 0.4253214442400451
MODEL_SETTINGS = {
'model_name': 'GradientBoostingRegressor',
'learning_rate': 0.550}
Mean Squared Error: 0.39587242367884334
MODEL_SETTINGS = {
'model_name': 'GradientBoostingRegressor',
'learning_rate': 0.650}
Mean Squared Error: 0.40041838873950636
| learning_rate | MSE |
|---|---|
| 0.100 | 0.4400 |
| 0.200 | 0.4142 |
| 0.300 | 0.4051 |
| 0.400 | 0.4012 |
| 0.500 | 0.3966 |
| 0.550 | 0.3958 |
| 0.600 | 0.4032 |
| 0.650 | 0.4004 |
| 0.700 | 0.3999 |
| 0.800 | 0.4253 |
| 1.000 | 0.4341 |
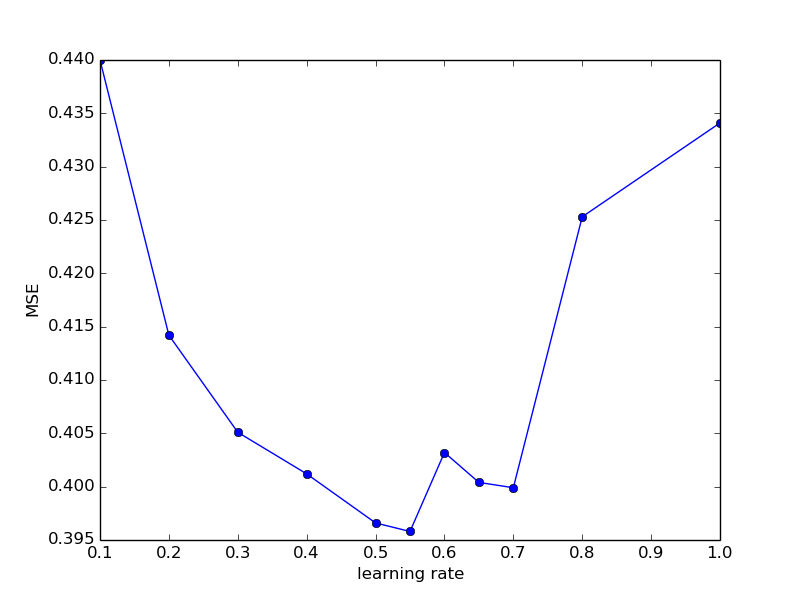
Похоже на то, что оптимиальное значение лежит где-то в районе 0.500 — 0.550 и изменения в ту или иную сторону по большому счету уже мало отражаются на итоговой метрике по сравнению с другими возможными изменениями параметров модели или списка фичей. Зафиксируем learning_rate на значении 0.550 и обратим внимание на другие параметры нашей модели.
Кстати, в аналогичных случаях для того, чтобы удостовериться в правильном подборе того или иного набора гиперпараметров, может быть полезно изменить имеющийся у многих алгоритмов параметр random_state или даже разделение выборки на тренировочную и валидационную при сохранении количеств элементов в них. Это поможет собрать больше информации о реальной эффективности алгоритма в случае не вполне четкой закономерности между настройками гиперпараметров и качеством предсказания на валидационной выборке.
| n_estimators: int (default=100)
| The number of boosting stages to perform. Gradient boosting
| is fairly robust to over-fitting so a large number usually
| results in better performance.
Количество неких «boosting stages» при обучении модели градиентного бустинга. Автор, если быть откровенным, уже подзабыл, какую роль они играют при формальном определении алгоритма, однако возьмем да проварьруем этот параметр. Кстати начнем засекать время, затрачиваемое на обучение модели.
import time
MODEL_SETTINGS = {
'model_name':'GradientBoostingRegressor',
'learning_rate':0.550,
'n_estimators':100}
model = GradientBoostingRegressor(learning_rate=MODEL_SETTINGS['learning_rate'],
n_estimators=MODEL_SETTINGS['n_estimators'])
time_start = time.time()
model.fit(numpy.array(train_samples), numpy.array(train_labels))
print('Time spent: {0}'.format(time.time() - time_start))
print('MODEL_SETTINGS = {{n {0}n {1}n {2}}}'
.format(MODEL_SETTINGS['model_name'],
MODEL_SETTINGS['learning_rate'],
MODEL_SETTINGS['n_estimators']))
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100}
Time spent: 71.83099746704102
Mean Squared Error: 0.39622103688045596
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 200}
Time spent: 141.9290111064911
Mean Squared Error: 0.40527237378150016
Как видим, время затраченное на обучение значительно выросло, а метрика качества только ухудшилась. На всякий случай все-таки попробуем еще раз увеличить параметр.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 300}
Time spent: 204.2548701763153
Mean Squared Error: 0.4027642069054909
Сложно, не понятно, давайте попробуем откатить все обратно и поискать другие точки роста.
| max_depth: integer, optional (default=3)
| maximum depth of the individual regression estimators. The maximum
| depth limits the number of nodes in the tree. Tune this parameter
| for best performance; the best value depends on the interaction
| of the input variables.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 100
'max_depth': 3}
Time spent: 66.88031792640686
Mean Squared Error: 0.39713231957974565
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 100
'max_depth': 4}
Time spent: 86.24338245391846
Mean Squared Error: 0.40575622943301354
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 100
'max_depth': 2}
Time spent: 45.39022421836853
Mean Squared Error: 0.41356622455188463
К сожалению, тоже не помогает — возвращаем на исходное значение и идем дальше.
| criterion: string, optional (default=«friedman_mse»)
| The function to measure the quality of a split. Supported criteria
| are «friedman_mse» for the mean squared error with improvement
| score by Friedman, «mse» for mean squared error, and «mae» for
| the mean absolute error. The default value of «friedman_mse» is
| generally the best as it can provide a better approximation in
| some cases.
Не помню, чтобы изменение этого параметра помогало улучшить модель, да и Воронцов на лекциях когда-то говорил, что изменение критерия разделения практически не влияет на качество итоговой модели, так что пропускаем и идем еще дальше.
| min_samples_split: int, float, optional (default=2)
| The minimum number of samples required to split an internal node:
|
| — If int, then consider `min_samples_split` as the minimum number.
| — If float, then `min_samples_split` is a percentage and
| `ceil(min_samples_split * n_samples)` are the minimum
| number of samples for each split.
|
|… versionchanged:: 0.18
| Added float values for percentages.
Минимальное количество примеров, необходимое для продолжения достраивания дерева в данной вершине при обучении. Попробуем изменить его.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 100
'max_depth': 3 'min_samples_split': 2
}
<source>
<code>Time spent: 66.22262406349182</code>
<code>Mean Squared Error: 0.39721489877049687</code>
Выглядит как прогресс - и, что немаловажно, не стоящий нам времени на обучение. Попробуем продолжить.
<source lang="python">
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3 ,
'min_samples_split': 3
}
Time spent: 66.18473935127258
Mean Squared Error: 0.39493122173406714
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor
'learning_rate': 0.55
'n_estimators': 100
'max_depth': 3
'min_samples_split': 8
}
Time spent: 66.7643404006958
Mean Squared Error: 0.3982469042761572
Прогресс закончился, так толком и не начавшись. Для полноты картины попробуем использовать промежуточное значение 4.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
}
Time spent: 66.75952744483948
Mean Squared Error: 0.3945186290058591
Совсем чуть-чуть лучше, чем при 3, но, тем не менее, с учетом, что по времени обучения разницы нет, оставим это значение.
| min_samples_leaf: int, float, optional (default=1)
| The minimum number of samples required to be at a leaf node:
|
| — If int, then consider `min_samples_leaf` as the minimum number.
| — If float, then `min_samples_leaf` is a percentage and
| `ceil(min_samples_leaf * n_samples)` are the minimum
| number of samples for each node.
|
|… versionchanged:: 0.18
| Added float values for percentages.
Минимальное количество примеров, которое может находиться в листе дерева после обучения. Увеличение этого параметра снижает качество предсказания на тренировочной выборке (т. к. при меньшем значении деревья, составляющие ансамбль в большей степени подстраиваются под каждый конкретный пример из обучающей выборки) и, если повезет, повышает качество на валидационной. То есть, по крайней мере теоретически, помогает бороться с переобучением.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
'min_samples_leaf': 1}
Time spent: 68.58824563026428
Mean Squared Error: 0.39465027476703846
Предсказание при подстановке значения параметра «по умолчанию» приблизительно совпадает с значением из предыдущего эксперимента. Это значит, что все в порядке, наша (пока что тривиальная) валидационная процедура возвращает значение действительно соответствующее качеству предсказания алгоритма, а стартовое значение параметра мы не перепутали.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
'min_samples_leaf': 2}
Time spent: 68.03447198867798
Mean Squared Error: 0.39707533548242
При увеличении параметра с 1 до 2 мы видим ухудшение метрики качества алгоритма. Все-таки попробуем его увеличить еще раз.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4,
'min_samples_leaf': 3,
'random_seed': 0}
Time spent: 66.98832631111145
Mean Squared Error: 0.39419555554861274
Несколько подозрительно, что увеличив параметр второй раз подряд мы, после ухудшения целевой метрики, увидели ее улучшение, да еще и превышающее исходное значение. Чуть выше мы получили весомое свидетельство в пользу того, что текущая валидационная процедура дает адекватную оценку качества предсказания, по крайней мере вплоть до четвертого знака после запятой. Проверим, что произойдет при изменении параметра random_seed.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4,
'min_samples_leaf': 3,
'random_seed': 1}
Time spent: 67.16857171058655
Mean Squared Error: 0.39483997966302
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
'min_samples_leaf': 3,
'random_seed': 2}
Time spent: 66.11015605926514
Mean Squared Error: 0.39492203941997045
Выглядит так, что валидационная процедура в самом деле дает адекватную оценку модели, по крайней мере до упомянутого выше четвертого знака после запятой. Значит очередная проба «для очистки совести» помогла, как ни удивительно видеть качество немонотонно зависящее от значения гиперпараметра. Стоит попробовать его увеличить еще раз.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
'min_samples_leaf': 4 ,
'random_seed': 0}
Time spent: 66.96864414215088
Mean Squared Error: 0.39725274882841366
Опять ухудшение. Может быть, дело в том, что при четных значениях параметра по каким-то волшебным причинам качество предсказания чуть хуже, чем при нечетных? Кто знает.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
'min_samples_leaf': 5 ,
'random_seed': 0}
Time spent: 66.33412432670593
Mean Squared Error: 0.39348528600652666
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4
'min_samples_leaf': 5 ,
'random_seed': 1}
Time spent: 66.22624254226685
Mean Squared Error: 0.3935675331843957
Качество еще немного улучшилось. А наша «гипотеза» касательно худшего качества предсказания при четных значениях получила еще одно подтверждение. Быть может, это не такая уж и случайность.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4,
'min_samples_leaf': 6 ,
'random_seed': 0}
Time spent: 66.88769054412842
Mean Squared Error: 0.38855940004423717
Все же при переходе от 5 к 6 качество еще немного улучшилось. С целью экономии места пропустим полные логи экспериментов, а сразу перенесем их результаты в таблицу и сгенерируем соответствующий график.
| min_samples_leaf | MSE | time spent |
|---|---|---|
| 1 | 0.3946 | 68.58 |
| 2 | 0.3970 | 68.03 |
| 3 | 0.3941 | 66.98 |
| 4 | 0.3972 | 66.96 |
| 5 | 0.3934 | 66.33 |
| 6 | 0.3885 | 66.88 |
| 7 | 0.3895 | 65.22 |
| 8 | 0.3903 | 65.89 |
| 9 | 0.3926 | 66.31 |
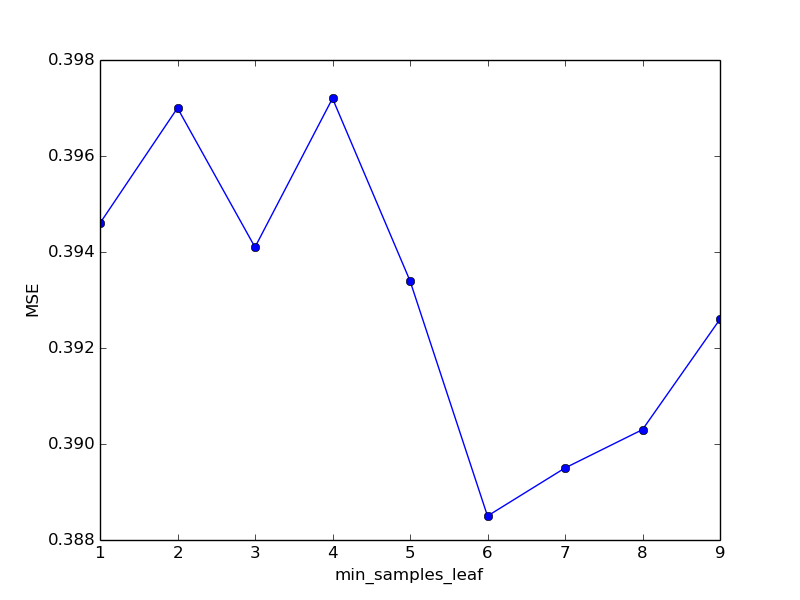
Учитывая высокий уровень доверия к полученным валидационным результатам, можно принять, что оптимальное значение min_samples_leaf равно 6. Перейдем к экспериментам со следующим параметром.
| min_weight_fraction_leaf: float, optional (default=0.)
| The minimum weighted fraction of the sum total of weights (of all
| the input samples) required to be at a leaf node. Samples have
| equal weight when sample_weight is not provided.
Минимальная часть примеров, необходимая для формирования листа. По умолчанию их количество равно нулю, то есть не задает никакого ограничения. По идее, увеличение значения этого параметра должно препятствовать переобучению, подобно параметру mean_samples_leaf.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4,
'min_samples_leaf': 6 ,
'random_seed': 0,
'min_weight_fraction_leaf': 0.01}
Time spent: 68.06336092948914
Mean Squared Error: 0.41160143391833687
Увы, качество предсказания ухудшилось. Но может быть, мы взяли слишком большое значение?
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4,
'min_samples_leaf': 6 ,
'random_seed': 0,
'min_weight_fraction_leaf': 0.001}
Time spent: 67.03254532814026
Mean Squared Error: 0.39262469473669265
Опять уменьшение нам не помогло. Вообще говоря, судя по описанию этого параметра, при выборке фиксированного размера будет действовать ограничение, либо заданное min_samples_leaf, либо заданное min_weight_fraction_leaf. Так что оставим его и перейдем к следующему.
| subsample: float, optional (default=1.0)
| The fraction of samples to be used for fitting the individual base
| learners. If smaller than 1.0 this results in Stochastic Gradient
| Boosting. `subsample` interacts with the parameter `n_estimators`.
| Choosing `subsample < 1.0` leads to a reduction of variance
| and an increase in bias.
MODEL_SETTINGS = {
'model_name': GradientBoostingRegressor,
'learning_rate': 0.55,
'n_estimators': 100,
'max_depth': 3,
'min_samples_split': 4,
'min_samples_leaf': 6,
'random_seed': 0,
'min_weight_fraction_leaf': 0.0,
'subsample': 0.9}
Time spent: 155.24894833564758
Mean Squared Error: 0.39231319253775626
Выглядит так, как будто простое варьирование параметров нам уже не помогает (и можно предположить, что больше почти не поможет). Для того, чтобы завершить этот этап, давайте сгенерируем сабмит для kaggle с помощью написанного в прошлый раз класса для обработки запросов. Разумеется, при решении задач на kaggle как правило используются варианты попроще, но для того, чтобы просимулировать ситуацию, возникающую в реальном приложении и протестировать написанный нами в прошлый раз класс, можно и потратить немного времени на написание дополнительного кода.
Генерируем файл с предсказанием
Под спойлером находится модификация скрипта generate_response.py.
import pickle
import numpy
import research
class FinalModel(object):
def __init__(self, model, to_sample, additional_data):
self._model = model
self._to_sample = to_sample
self._additional_data = additional_data
def process(self, instance):
return self._model.predict(numpy.array(self._to_sample(
instance, self._additional_data)).reshape(1, -1))[0]
if __name__ == '__main__':
with open('./data/model.mdl', 'rb') as input_stream:
model = pickle.loads(input_stream.read())
additional_data = research.load_additional_data()
final_model = FinalModel(model, research.to_sample, additional_data)
# print(final_model.process({'tube_assembly_id':'TA-00001', 'supplier':'S-0066',
# 'quote_date':'2013-06-23', 'annual_usage':'0',
# 'min_order_quantity':'0', 'bracket_pricing':'Yes',
# 'quantity':'1'}))
list_of_predictions = []
with open('./data/competition_data/test_set.csv') as input_stream:
header_line = input_stream.readline()
column_names = header_line[:-1].split(',')
for line in input_stream:
cell_values = line[:-1].split(',')
# new_id = cell_values[column_names.index('id')]
new_id = cell_values[0] # id column
new_instance = dict(zip(column_names[1:], cell_values[1:]))
new_prediction = final_model.process(new_instance)
list_of_predictions.append((new_id, new_prediction))
with open('./data/output.csv', 'w') as output_stream:
output_stream.write('id,costn')
for prediction in list_of_predictions:
output_stream.write(prediction[0] + ',' + str(prediction[1]) + 'n')
В качестве входящих данных скрипт использует модель, сгенерированную скриптом research.py и файл с тестовыми данными test_set.csv, находящийся в архиве, предоставленном организаторами соревнования. На выходе он герерирует файл output.csv. Отсутствие изменений, связанных с формированием предсказания в файле generate_response.py иллюстрирует гибкость схемы тренировочного и исполняемого (serving) пайплайнов. Несмотря на то, что мы подобрали ряд новых фичей, сменили модель, использовали новый, ранее не применявшийся, файл с данными, в части кода, относящейся к применению модели ничего по существу не поменялось.
Соревнование на kaggle уже закончилось, но мы все равно можем проверить, насколько оценка платформы совпадает с нашими валидационными надеждами здесь.
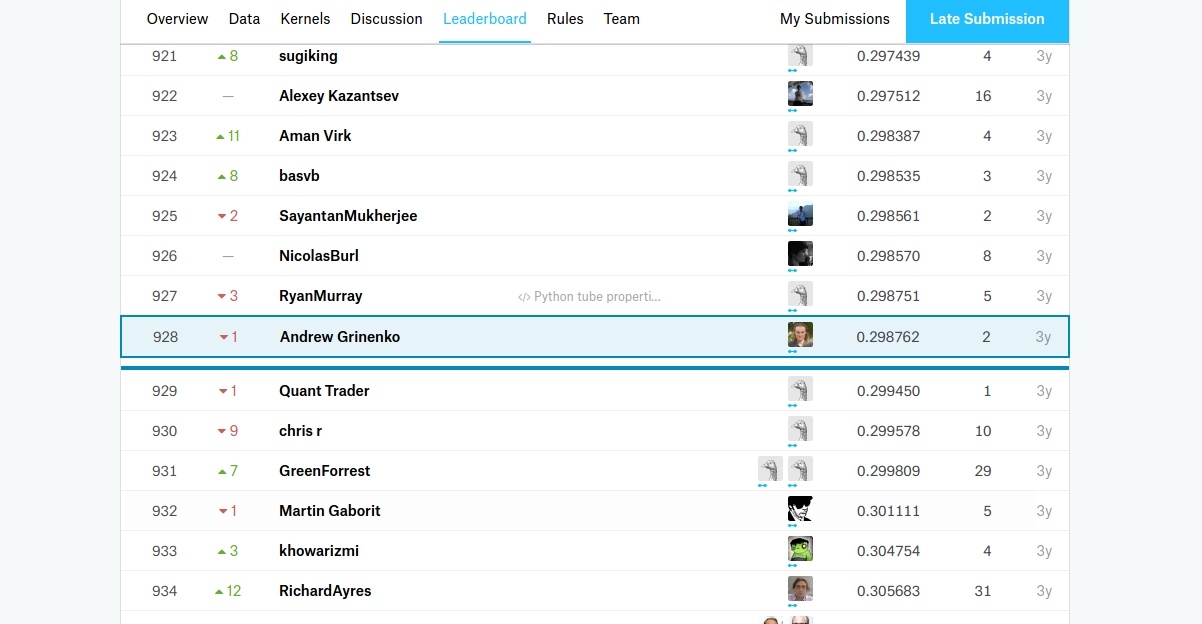
Результат, на первый взгляд, обнадеживающий — качество предсказания оказалось даже выше, чем на валидации. Однако, с одной стороны, результат на публичном лидерборде слишком сильно превышает полученный на валидации, а с другой — наше место в общем зачете (относительно момента завершения соревнования) все еще не слишком высоко. Однако оставим решение обоих этих вопросов на другой раз.
Вывод
Итак, мы оптимизировали алгоритм предсказания, попробовали разные модели, обнаружили что столь широко разрекламированные нейросети не очень подходят для нашей задачи, поэкспериментировали с выбором гиперпараметров, и, наконец, сформировали первый файл с предсказаниями для kaggle. Не так уж и мало для одной статьи, увидимся в следующий раз!
Автор: Андрей Гриненко






