Задачка конечно так себе, если речь идет об одном параллелепипеде и одной плоскости. Ведь всё просто: возьмем бумажку, ручку, нарисуем и всё посчитаем. Но бывает, что нужно объяснить машине как вычислить такой объем. И еще их тысячи тысяч. Тогда одни вдумчиво садятся и дотошно рассматривают все возможные случаи сечения, расписывают алгоритм. Другие, более нетерпеливые, призывают Монте-Карло. А третьи, самые хитрые, которым надо быстро и точно — используют формулы. Вот такие:
-2D (прямая: a, b, c и прямоугольник: x0, x1, y0, y1)
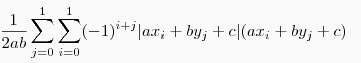
-3D (плоскость: a, b, c, d и прямоугольный параллелепипед: x0, x1, y0, y1, z0, z1)
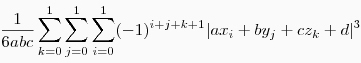
Вот к этим формулам надо прибавить объем (в 2D — площадь прямоугольника) параллелепипеда и поделить пополам, тогда получится то, что ищем.
Получено всё это счастье интегрированием функции f(x,y,z)/|f(x,y,z)| по объему параллелепипеда, где f — уравнение плоскости.
Формулы честные: сам вывел, сам делюсь.
Автор: FransuaMaryDelone




