Снижение сложности вычислений при операциях с векторами и матрицами

в 20:17, , рубрики: c++, вектор, векторная алгебра, высокая производительность, вычислительная сложность, математика, матрица, матрицы, операторы, оптимизация, счетчик ссылок

Введение

Ввиду того, что при решении задач оптимизации, дифференциальных игр, и в 2D и 3D расчётах, а вернее при написании софта, который проводит вычисления для их решения одними из наиболее часто выполняемых операций являются векторно-матричные преобразования типа $aX+bY$, где $a,b$ — скалярные значения, $X, Yin R^n$ — вектора или матрицы размерности $R^{ntimes m}$.
Собственно вот такие:
image
(источник).

Так, чтобы не углубляться в теорию оптимизации за примерами достаточно вспомнить формулу численного интегрирования Рунге-Кутты четвёртого порядка:

$Y_{n+1}=Y_n+frac{h}{6}(k_1 + 2 k_2 + 2 k_3+k_4),$

где $Y_i$ — очередное значение интегрируемой функции $f(t,Y)$ $h$ — шаг метода, а $k_i$, $i=1..4$ — значения интегрируемой функции в некоторых промежуточных точках — в общем случае векторах.

Как можно заметить основную массу математических операций как для векторов, так и для матриц составляют:

  • сложение и вычитание — более быстрые;
  • умножение и деление — более медленные.

О сложности вычислений хорошо написано в соответствующем курсе МФТИ.

Помимо этого, довольно существенные расходы при реализации векторных вычислений приходятся на операции управления памятью — создание и уничтожение массивов представляющих собой матрицы и вектора.

Соответственно есть смысл заняться снижением количества операций привносящих наибольшую сложность — умножения (математика) и операции управления памятью (алгоритмика).

Снижение вычислительной сложности

Произвольный вектор $xin R^n$ представим в виде $x=aX$, где
$ain R^1$, $Xin R^n$, обозначим как $[a,X]$. Операцией приведения такого вектора назовем вычисление $[a,X]=xin R^n$, — обратную операцию, вычислительная сложность которой составляет $n$ операций действительного умножения.

Соответственно под экономией будем понимать экономию операций умножения.

На чём можно сэкономить при операциях с векторами :

  1. Умножение на константу $b[a,X]=[ab,X]$ — экономится $n-1$ операция умножения.
  2. Сложение $k$ сонаправленных векторов $sumlimits_{i=1}^{k} [a_i,X]=left[sumlimits_{i=1}^{k}a_i,Xright]$
    • откладывается вычисление $n$ умножений;
    • экономится $(k-2)n$ умножений.
  3. Сложение не сонаправленных векторов $[a,X]+[b,Y]=[a,X+b/a Y]$ — откладывается вычисление $n-1$ операция умножения, при $a ne 0$.
  4. Умножение матрицы на вектор: $A[a,x]=[a,Ax]$, где $Ain R^{mtimes n}$ — что позволяет отложить вычисление $m$ операций умножения.
  5. Скалярное произведение векторов $([a,X],[b,Y])=ab(X,Y)$ — экономится $n-1$ операция действительного умножения.

Аналогично, если представить матрицу в виде $Y=abar Y$, где
$ain R^1$, а $bar Y, Yin R^{ntimes m}$, обозначим как $[a,bar Y]$. Соответственно операцией приведения — вычисление $[a,bar Y]=Yin R^{ntimes m}$, — обратную операцию, вычислительная сложность которой составляет $ncdot m$ операций действительного умножения.

Аналогичны и возможности экономии (1-4) с той той лишь разницей, что операция скалярного произведения (5) отсутствует, а для остальных операций возможности сэкономить умножения становится больше в $m$ раз, что довольно приятно, особенно при необходимости хранения в матричном представлении массивов векторов для проведения над ними различных массовых операций.

Понятно, что приведенные выше способы экономии не бесплатны в смысле необходимости иметь дополнительную память для хранения коэффициентов, и накладных затрат связанных с контролем состояния вычисляемых объектов.

Помимо чисто математических оптимизаций данный подход вполне применим при вычислениях на сетках т.е., например, если значение сеточной функции, представленной вектором, надо сначала умножить на некоторую константу, а потом найти градиентным методом (не перебирая все значения) её максимум.

Снижение алгоритмической сложности

Как видно из предшествующих рассуждений, — реальная экономия возникает для:

  • умножения вектора/матрицы на число и скалярных произведений векторов;
  • операций над векторами и матрицами, отличающимися только коэффициентами.

Соответственно для того, чтобы обеспечить оптимизацию скалярных вычислений необходимо построить структуру данных следующего вида:

class Vector {
public:
   sVec *v; //массив для данных
   double upd; //коэфф. a
   bool updated; //признак  того, что a==1
//....
};

Возможно не самым очевидное здесь — назначение переменной updated, ввиду того, что если upd = 1, то вроде как дополнительные проверки избыточны. Но если вспомнить, что последовательное деление и умножение следующего вида:

a_ /= b_;
a_ *= b_;

не обязано сохранять значение a_ из-за округлений, то видно, что данная страховка не лишняя.

Далее, если обратить внимание на, то, что если у векторов $[a,X]$ и $[b,X]$ сам $X$ одинаков, то нет смысла хранить его дважды, а достаточно создать единственный объект класса базовый вектор $X$ и ссылаться на него в расчётах, т.е. 

class sVec {
public:
    unsigned long size;
    double *v;//собственно массив данных
    long linkCount;//счётчик ссылок
//..
};

image

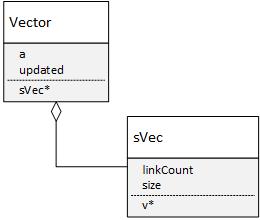
Динамический массив здесь необходим для того, чтобы отрабатывать склонность векторов менять размерность при умножении на матрицу, подход связанный с учётом ссылок — для того, чтобы убрать "под капот" логику связанную с созданием и отслеживанием дубликатов объектов, при использовании перегруженных операторов для векторных и матричных операций в С++.

Особенности реализации

Для примера (который можно взять на github) рассмотрим достаточно простые вычисления, связанные с векторно-матричной арифметикой в разрезе экономии операций умножения. Итак: сначала создадим необходимые объекты:

    Vector X(2), Y(2), Z(2); //три вектора из R^2
    double a = 2.0; // коэфф. для проверки умножения на скаляр

и инициализируем их как единичный вектор для X=[1,1] и нулевой для Y=[0,0]

    X.one(); //единичный вектор [1,1]
    Y.zero();// создаём нулевой вектор [0,0]
    cout<<"Вектор X: "<<X<<" Счётчик ссылок X: "<<X.v->linkCount<<" Адрес массива: "<<X.v<<endl;
    cout<<"Вектор Y: "<<Y<<" Счётчик ссылок Y: "<<Y.v->linkCount<<" Адрес массива: "<<Y.v<<endl;

Получаем, что внутренние вектора указывают на разыве массивы и оба счётчика ссылок равны единице.

Вектор X: [1,1]; Счётчик ссылок X: 1 Адрес массива: 448c910
Вектор Y: [0,0]; Счётчик ссылок Y: 1 Адрес массива: 448c940

Далее приравниваем вектора:

    Y=X;// теперь приравниваем X и Y
    cout<<"Вектор X: "<<X<<" Счётчик ссылок X: "<<X.v->linkCount<<" Адрес массива: "<<X.v<<endl;
    cout<<"Вектор Y: "<<Y<<" Счётчик ссылок Y: "<<Y.v->linkCount<<" Адрес массива: "<<Y.v<<endl;

и видим, что теперь оба вектора указывают на один и тот же адрес, а счётчик ссылок увеличился на 1:

Вектор X: [1,1];  Счётчик ссылок X: 2 Адрес массива: 448c910
Вектор Y: [1,1];  Счётчик ссылок Y: 2 Адрес массива: 448c910

После чего домножаем вектор X на 2 

    X*=a;  //домножаем вектор на коэффициент 2.0
    cout<<"Вектор X: "<<X<<" Счётчик ссылок X: "<<X.v->linkCount<<" Адрес массива: "<<X.v<<" Коэфф. a вектора X: "<<X.upd<<endl;
    cout<<"Вектор Y: "<<Y<<" Счётчик ссылок Y: "<<Y.v->linkCount<<" Адрес массива: "<<Y.v<<" Коэфф. a вектора Y: "<<Y.upd<<endl;

и получаем, что несмотря на то, что оба вектора как и раньше указывают на один и тот же адрес, и счётчик ссылок как и прежде 2, у .X сохранённый коэффициент 2, а у Y соответственно равен 1:

Вектор X: [2,2]; Счётчик ссылок X: 2 Адрес массива: 448c910 Коэфф. a вектора X: 2
Вектор Y: [1,1]; Счётчик ссылок Y: 1 Адрес массива: 448c910 Коэфф. a вектора Y: 1

И в конце, сложив X+Y 

    Z= X+Y;
    cout<<"Вектор Z: "<<Z<<" Счётчик ссылок Z: "<<Z.v->linkCount<<" Адрес массива: "<<Z.v<<" Коэфф. a вектора Z: "<<Z.upd<<endl;

получаем Z=[3,3]:

Вектор Z: [3,3]; Счётчик ссылок Z: 1 Адрес массива: 448c988 Коэфф. a вектора Z: 1

Для матриц все вычисления аналогичны:

    Matrix X_(2), Y_(2), Z_(2); //создаём 3 единичных диагональных матрицы 2x2

    cout<<"Матрица X: "<<endl<<X_<<" Счётчик ссылок X: "<<X_.v->linkCount<<" Адрес массива: "<<X_.v<<endl;
    cout<<"Матрица Y: "<<endl<<Y_<<" Счётчик ссылок Y: "<<Y_.v->linkCount<<" Адрес массива: "<<Y_.v<<endl;

    Y_=X_;// теперь приравниваем X_ и Y_
    cout<<"Матрица X: "<<endl<<X_<<" Счётчик ссылок X: "<<X_.v->linkCount<<" Адрес массива: "<<X_.v<<endl;
    cout<<"Матрица Y: "<<endl<<Y_<<" Счётчик ссылок Y: "<<Y_.v->linkCount<<" Адрес массива: "<<Y_.v<<endl;

    X_*=a;  //домножаем матрицу на коэффициент 2.0
    cout<<"Матрица X: "<<endl<<X_<<" Счётчик ссылок X: "<<X_.v->linkCount<<" Адрес массива: "<<X_.v<<" Коэфф. a матрицы X: "<<X_.upd<<endl;

    Z_= X_+Y_;
    cout<<"Матрица Z: "<<endl<<Z_<<" Счётчик ссылок Z: "<<Z_.v->linkCount<<" Адрес массива: "<<Z_.v<<" Коэфф. a матрицы Z: "<<Z_.upd<<endl;

Вывод также аналогичен:

Матрица X:
[1,0]
[0,1];
 Счётчик ссылок X: 1 Адрес массива: 44854a0
Матрица Y:
[1,0]
[0,1];
 Счётчик ссылок Y: 1 Адрес массива: 44854c0
Матрица X:
[1,0]
[0,1];
 Счётчик ссылок X: 2 Адрес массива: 44854a0
Матрица Y:
[1,0]
[0,1];
 Счётчик ссылок Y: 2 Адрес массива: 44854a0
Матрица X:
[2,0]
[0,2];
 Счётчик ссылок X: 2 Адрес массива: 44854a0 Коэфф. a матрицы X: 2
Матрица Z:
[3,0]
[0,3];
 Счётчик ссылок Z: 1 Адрес массива: 4485500 Коэфф. a матрицы Z: 1

Библиотечка доступна на GitHub.

Пользуйтесь, критикуйте.

Автор: Алексей

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js