По роду деятельности (учеба в школе) иногда порешиваю олимпиадные задачи. Недавно столкнулся с таким экземпляром:
Найти количество цифр в записи факториала натурального числа N.
Ограничения: 0<n<=1000000; время: 5с.
На первый взгляд ничего сложного. Вооружившись длинной арифметикой быстренько накидал решение… Но не тут-то было. Даже 10000 не укладывались в 5 секунд. «Что-то не так», — подсказал Капитан Очевидность.
Что это было
Полазил по форумах, поговорил с умными людьми. Кто-то вскользь упомянул некую формулу Стирлинга.
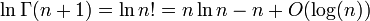
Ссылка на статью о ней внизу.
Но я был полон скептики: «Задача-то со школьной олимпиады. Какой Стирлинг?» Продолжал думать. Искал варианты быстрой длинной арифметики… Но вы сами понимаете, что зря. Я тоже. Уже.
После повторного общения на форумах вырисовалась функция:
unsigned f(unsigned n)
{
const double
pi = 3.14159265358979323846,
e = 2.7182818284590452354;
return std::ceil(std::log10(2 * pi * n) / 2 + n * (std::log10(n / e)));
}«Ладно, будем считать, что эту задачу сперли с учебника второкурсника», подумал я и слампичил «программку».
#include <iostream>
#include <cmath>
using namespace std;
unsigned f(unsigned n)
{
const double
pi = 3.14159265358979323846,
e = 2.7182818284590452354;
return std::ceil(std::log10(2 * pi * n) / 2 + n * (std::log10(n / e)));
}
int main()
{
unsigned n;
cin>>n;
cout<<f(n);
}
Как ни странно, она проходила все тесты, кроме одного. После недолгих раздумий родился элегантный костыль:
#include <iostream>
#include <cmath>
using namespace std;
unsigned f(unsigned n)
{
const double
pi = 3.14159265358979323846,
e = 2.7182818284590452354;
if (n==1 || n==0)
{
return 1;
}
else
{
return std::ceil(std::log10(2 * pi * n) / 2 + n * (std::log10(n / e)));
}
}
int main()
{
unsigned n;
cin>>n;
cout<<f(n);
}
На этом аккорде судьба задачи стала решенной и она перекочевала в мой архив. А формула Стирлинга теперь висит у меня в рамочке. Чего и вам желаю. Может, пригодится и вам.
Стирлинг засветился на вики
Автор: Izobara
