Динамическая идентификация объектов управления

Введение

Идентификация объектов управления — совокупность методов для построения математических моделей объекта по данным наблюдений.

Математическая модель в данном контексте означает математическое описание поведения какого-либо объекта или процесса в частотной или временной области, к примеру, физических процессов (движение механической системы под действием внешней силы [1]), экономического процесса (влияние смены курса валют на потребительские цены на товары [2]).

В настоящее время эта область теории управления находит широкое применение на практике и поэтому интересна для рассмотрения.

Область динамической идентификации объектов управления в связи с различной природой самих объектов достаточно обширна, поэтому для начала ограничимся рассмотрением методов обработки так называемой кривой разгона.

Кривой разгона называют процесс изменения во времени выходной переменной, вызванный ступенчатым входным воздействием. Кривая разгона служит для определения динамических свойств объекта.

Постановка задачи

1.Построить математические модели динамической идентификации объекта управления по нормированной переходной характеристике (кривой разгона):
• Методом наименьших квадратов с использованием производных;
• Модифицированным методом площадей.
2. Определить и сравнить адекватность полученных математических моделей объекту управления.

Теория
Идентификация состоит в отыскании для объекта адекватной ему модели. Различают структурную и параметрическую идентификацию. При структурной идентификации определяется форма модели из некоторого заданного класса функций, при параметрической идентификации определяются параметры модели.

Если выходные сигналы объекта Y(t) полностью определяются наблюдаемыми входными воздействиями X(t), то для его идентификации достаточно использовать методы активного эксперимента.

Исходной информацией является экспериментально снятая кривая разгона – реакция объекта Y(t) на поданное входное воздействие X(t) в интервале времени 0≤t≤T.

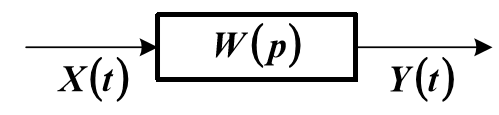
Это структурная схема модели объекта с операторной передаточной функцией W(p). Уравнение динамической характеристики объекта можно условно представить в следующем виде:

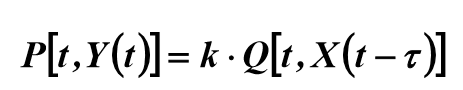(1)

где 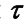– время запаздывания объекта, которое проходит от момента подачи сигнала на вход объекта до момента появления сигнала на его выходе; k – коэффициент усиления (или коэффициент передачи) объекта.

Схема для определения времени запаздывания и коэффициента усиления объекта:

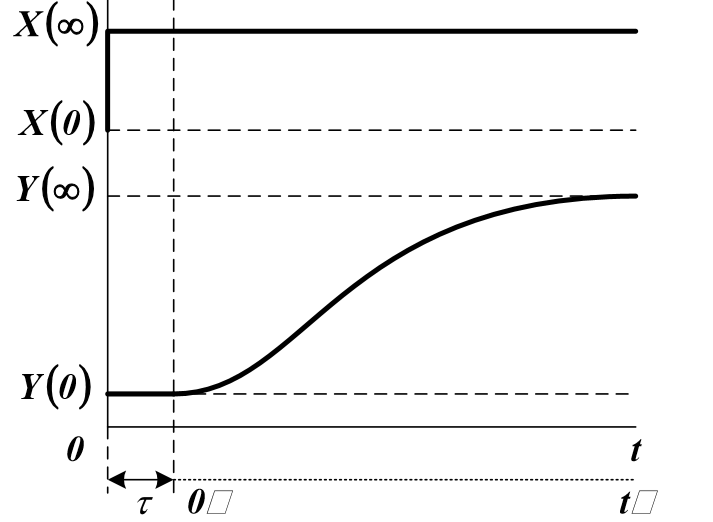
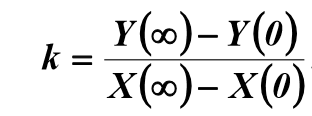
Входные и выходные величины, как правило, масштабируются в стандартном диапазоне от 0 до 1 (нормируются):

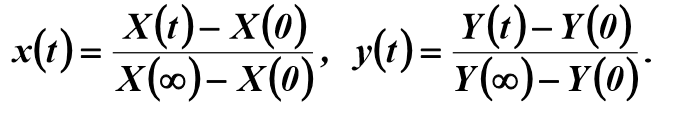
После определения k и 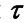можно исследовать объект в нормированных координатах и без запаздывания, сместив шкалу времени вправо на величину 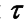[3].

Структурная идентификация объекта

При структурной идентификации априорная информация об объекте используется для определения структуры модели.

Уравнение динамики, как правило, выбирается из класса линейных или линеаризованных характеристик. В нормированных координатах модель объекта с сосредоточенными параметрами, одним входным и одним выходным сигналом является обыкновенным дифференциальным уравнением с постоянными коэффициентами:

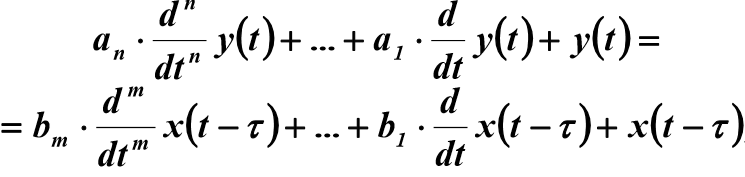(2)

где коэффициенты 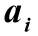и 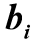имеют размерность времени в степени, равной порядку производной соответствующего слагаемого. В физически реализуемых системах n≥m

По виду кривой разгона можно приближённо определить порядок будущей модели, например, для объекта первого порядка:

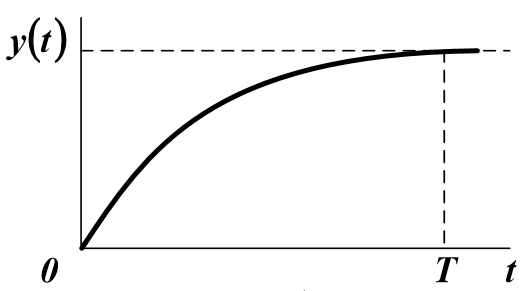
Для объектов более высоких порядков:

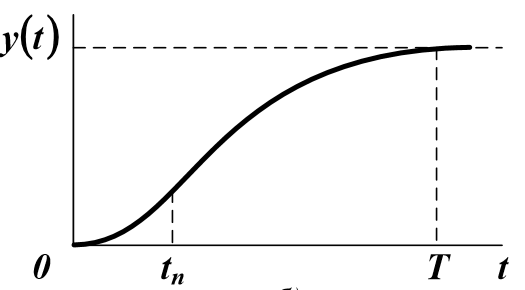
Обычно X(t) – ступенчатая функция, поэтому порядок уравнения (1) может быть приближенно определен по форме кривой разгона объекта. Если эта характеристика не имеет точек перегиба, то n = 1. Если есть перегиб при t = tп, и tп / T <0,1...0,15, то n = 2.В противном случае считают n> 2. Однако можно снизить порядок модели, вводя фиктивное запаздывание.

Вывод

Влияние погрешности измерения X(t) и Y(t) и погрешности численных методов обработки информации обычно делает нецелесообразным использование моделей выше третьего-четвертого порядка.

Параметрическая идентификация объекта

При параметрической идентификации данные об объекте обрабатываются для получения о нем апостериорной информации. При этом оцениваются параметры выбранной модели. В простейших случаях такая оценка может выполняться по графику переходной характеристики.

Параметрическая идентификация методом наименьших квадратов с использованием производных

Для идентификации объекта произвольного порядка используется метод наименьших квадратов, требующий минимизации среднего квадрата невязки правой и левой частей уравнения (2):

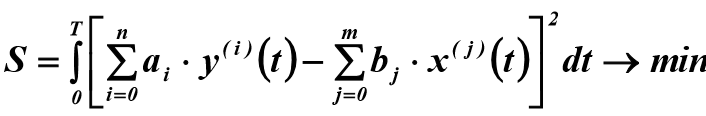(3)

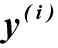где: и 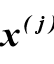– производные i-го и j-го порядка от функций выходного и входного сигналов.

Решение задачи (3) сводится к решению системы:

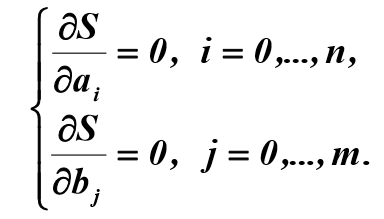(4)

Преобразуя (4) в соответствии с уравнением (3), можно получить систему линейных алгебраических уравнений:

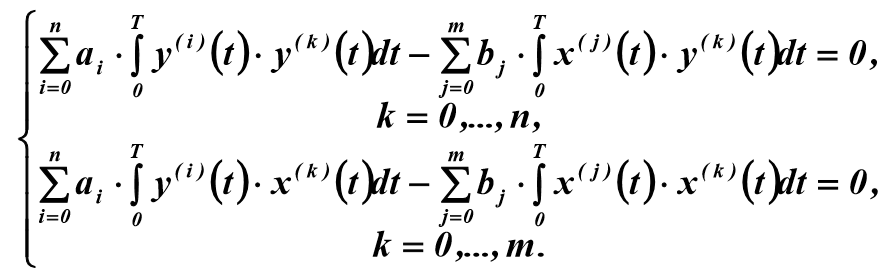(5)

Для решения системы (5) относительно неизвестных параметров 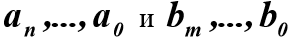необходимо знать производные входного и выходного сигналов объекта, которые находятся в результате сглаживания функций X(t) и Y(t) на отрезке 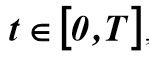. Для расчета коэффициента 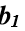используется формула:

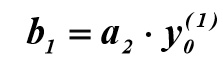
Вывод

Погрешность численного дифференцирования, как правило, достаточно высока, поэтому схему определения коэффициентов,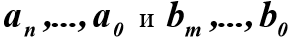 нужно использовать дифференцирование аналитических выражений для X(t) и Y(t).

Параметрическая идентификация модифицированным методом площадей

Для создания модели средствами Python, модификация метода площадей состоит в неизменном масштабе времени. В классическом варианте вводят новый масштаб времени, что при численном решении приводит к дополнительной погрешности.

Обычно, выражение для передаточной функции ищут в виде одной из трех математических моделей:

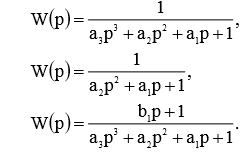
Выражение 1/W(p), обратное передаточной функции модели, можно разложить в ряд по степени р:

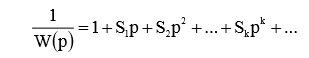
Коэффициенты a,b приведенных передаточных функций связаны с коэффициентами S следующей системой уравнений:

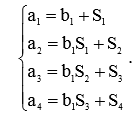
Коэффициенты Si связаны с переходной функцией h(t) соотношениями:

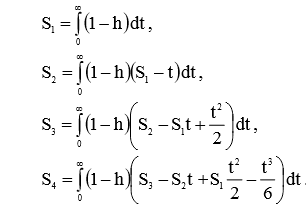(6)

Вывод

Соотношения (6) оптимальны для решения средствами Python при интерполяции h(t) кубическими сплайнами, что будет доказано на примерах.

Оценка адекватности математических моделей идентификации объектов управления

Для выбора оптимальной модели достаточно использовать показатель адекватности второго порядка:

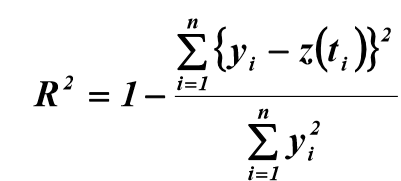(7)

где 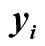– данные, снятые с кривой разгона, 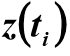– значения, рассчитанные по действительной части Re(W(i×w)) передаточной функции модели (переход из частотной области во временную):

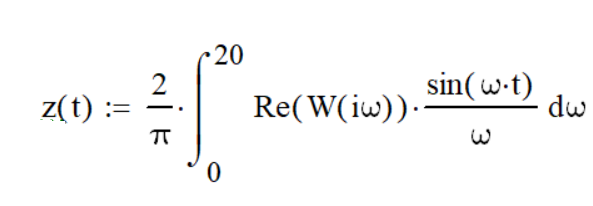(8)

Лучшей следует считать модель, обеспечивающую максимальное значение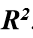

Учитывая существенную погрешность численного дифференцирования при решении системы уравнений (5), реализуем символьное дифференцирование. Для этого применим интерполяцию полиномом в соответствии со следующим листингом:

# -*- coding: utf8 -*-
import matplotlib.pyplot as plt# для построение графика
import time
start = time.time()
import scipy as sp# для интерполяции полиномом
import numpy as np# для операций с матрицами производных от КР
from sympy import *# для символьного дифференцирования КР
import scipy.integrate as spint
from scipy.integrate import quad
x=[0.0, 0.4, 0.8, 1.2, 1.6 ,2.0, 2.4, 2.8 ,3.2, 3.6]#время
y=[0.00, 0.11, 0.36, 0.61, 0.79, 0.89, 0.94, 0.98, 0.99, 1.00]# отклик системы
fp, residuals, rank, sv, rcond = sp.polyfit(x, y,4, full=True)# интерполяция полиномом
a=round(fp[0],4);b=round(fp[1],4);c=round(fp[2],4)
d=round(fp[3],4);e=round(fp[4],4)
t=symbols('t ' ,real=True)
def h(t):# аналитическая форма переходной характеристики h(t)
         return a*t**4+b*t**3+c*t**2+d*t+e
''' Символьное вычисление производных'''
L1=integrate(h(t).diff(t)*h(t).diff(t,t),(t,0,3.6)) 
L2=integrate(h(t).diff(t,t)*h(t).diff(t,t),(t,0,3.6))
L3=integrate(h(t).diff(t)*h(t).diff(t),(t,0,3.6))
L4=integrate((1-h(t))*h(t).diff(t,t),(t,0,3.6))
L5=integrate((1-h(t))*h(t).diff(t),(t,0,3.6))
""" Матричная форма решения системы уравнений (5) с учётом критерия (3)"""
P= np.zeros([2,2])
P[0,0]=L2;P[0,1]=L1
P[1,0]=L1;P[1,1]=L3
Q= np.zeros([2,1])
Q[0,0]=L4;Q[1,0]=L5
P=np.matrix(P);
Q=np.matrix(Q)
C=P.I*Q
''' Коэффициенты передаточной функции объекта'''
a2=C[0,0]
a1=C[1,0]
b1=C[0,0]*h(t).diff(t).subs(t,0)
a2=round(C[0,0],3)
a1=round(C[1,0],3)
b1=round(C[0,0]*h(t).diff(t).subs(t,0),3)    
""" Переход из частотной области во временную по соотношению (8)"""
def ff(x,t):
        j=(-1)**0.5
        return (2/np.pi)*( ((b1*x*j+1)/(a2*(x*j)**2+a1*x*j+1)).real)*(np.sin(x*t)/x)
z=np.array([round(quad(lambda x: ff(x,t),0, 20)[0],2) for t in x])
"""Определение адекватности модели идентификации по соотношению (7) """
k=round(1-sum([(y[i]-z[i])**2 for i in np.arange(0,len(y)-1,1)])/sum([(y[i])**2 for i in np.arange(0,len(y)-1,1)]),5)
stop = time.time()
print ("Время работы программы :",round(stop-start,3))
plt.title('Идентификация методом наименьших квадратовn Адекватность модели -%s'%k)
plt.plot(x, y,'o', label='Снятая экспериментально КР')
plt.plot(x, z,'r', label=' W=(%s*p+1)/(%s*p**2+%s*p+1)'%(b1,a2,a1))
plt.legend(loc='best')
plt.grid(True)
plt.show()

Получим:

Время работы программы: 0.802

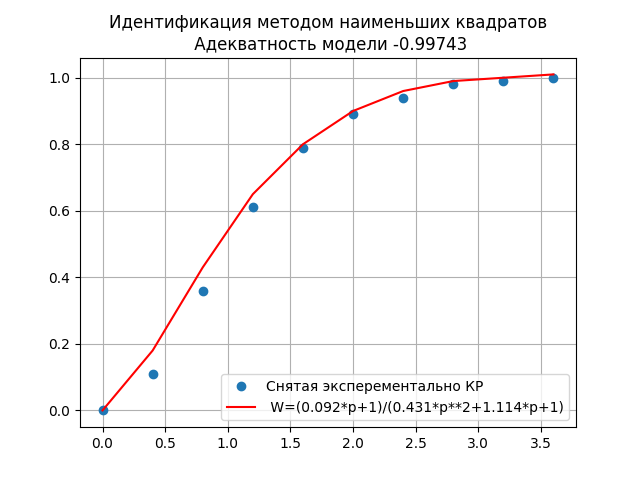
Высокая степень адекватности модели 0.99743 свидетельствует о том, что полученная передаточная функция:

W=(0.092*p+1)/(0.431*p**2+1.114*p+1),

достаточно точно отображает динамические свойства объекта.

Кривая разгона получена экспериментально, поэтому дельнейшие исследование систем управления объектом на устойчивость [4] и определения параметров регуляторов [5] приобретают практическое значение.

Реализация средствами Python задачи идентификации объекта модифицированным методом площадей

Для решения этой задачи можно использовать численные методы поскольку модель не содержит дифференцирования, а предложенный метод решения согласно соотношениям (6) не предполагает смены координаты времени. Кроме этого, применим интерполяцию сплайном в соответствии со следующим листингом:

# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
import time
start = time.time()
from scipy.interpolate import splev, splrep
import scipy.integrate as spint
import numpy as np
from scipy.integrate import quad
xx =np.array([0.0, 0.4, 0.8, 1.2, 1.6 ,2.0, 2.4, 2.8 ,3.2, 3.6])
yy =np.array([0.00, 0.11, 0.36, 0.61, 0.79, 0.89, 0.94, 0.98, 0.99, 1.00])
""" Интерполяция переходной характеристики при помощи сплайнов"""
def h(x):         
         spl = splrep(xx , yy )
         return splev(x, spl)
""" Численное интегрирование без смены координаты времени в соответствии с (6)"""
S1=(spint.quad(lambda x:1-h(x),xx[0],xx[len(xx)-1])[0])
S2=(spint.quad(lambda x:(1-h(x))*(S1-x),xx[0],xx[len(xx)-1])[0])
S3=(spint.quad(lambda x:(1-h(x))*(S2-S1*x+(1/2)*x**2),xx[0],xx[len(xx)-1])[0])
S4=(spint.quad(lambda x:(1-h(x))*(S3-S2*x+S1*(1/2)*x**2-(1/6)*x**3),xx[0],xx[len(xx)-1])[0])
""" Определение коэффициентов передаточной функции"""
b1=-S4/S3
a1=b1+S1
a2=b1*S1+S2
a3=b1*S2+S3
""" Возврат во временную область"""
def ff(x,t):
        j=(-1)**0.5
        return (2/np.pi)*( ((b1*x*j+1)/(a3*(x*j)**3+a2*(x*j)**2+a1*x*j+1)).real)*(np.sin(x*t)/x)
y=np.array([round(quad(lambda x: ff(x,t),0, 20)[0],2) for t in xx])
""" Определение критерия адекватности модели ""
k=round(1-sum([(yy[i]-y[i])**2 for i in np.arange(0,len(yy)-1,1)])/sum([(yy[i])**2 for i in np.arange(0,len(yy)-1,1)]),5)
stop = time.time()
print ("Время работы программы :",round(stop-start,3))
plt.title('Идентификация модифицированным методом площадей.n Адекватность модели -%s'%k)
plt.plot(xx, yy,'o', label='Нормированная кривая разгона (КР)')
plt.plot(xx, y,'r', label='W=(%s*p+1)/(%s*p**3+%s*p**2+%s*p+1)'%(round(b1,3),round(a3,3),round(a2,3),round(a1,3)))
plt.legend(loc='best')
plt.grid(True)
plt.show()

Получим:

Время работы программы: 0.238

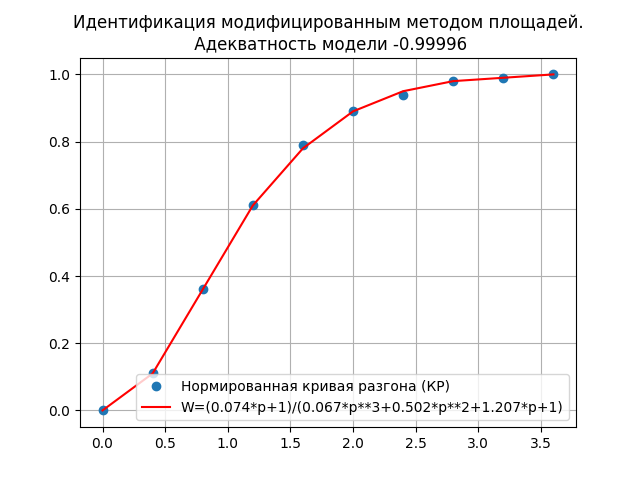
Высокая степень адекватности модели 0.99996 и большее быстродействие, чем при символьном дифференцировании, позволяет утверждать, что передаточная функция:

W= (0.074*p+1)/(0.067*p**3+0.502*p**2+1.207*p+1)),

полученная модернизированным методом площадей лучше отображает динамические свойства объекта.

Выводы

1. Публикация знакомит с основами динамической идентификации объекта управления.

2.Реализация решения задачи идентификации на свободно распространяемом языке программирования Python с примерами использования явного представления переходной функции полиномом и сплайнами будет способствовать расширению области применения Python.

3. Для численных решений задач идентификации, можно предложить использование соотношений (6), которые позволяют получить результат без изменения координаты времени.

Ссылки

1. Модель колебательного звена с применением символьного и численного решений дифференциального уравнения на SymPy и NumPy.
2. Математическая модель динамики финансового рынка.
3. Определение параметров модели методом площадей.
4. Определение устойчивости систем автоматического управления промышленными роботами.
5. Модель ПИД регулятора на Python.

Автор: Scorobey

Источник