Бинарная матричная нейронная сеть

Предлагается вариант искусственной нейронной сети в виде матрицы, входами и выходами которой являются наборы битов, а нейроны реализуют функции двоичной логики нескольких переменных. Такая сеть значительно отличается от сетей перцептронного типа и может дать такие преимущества как конечное число вариантов полного перебора функций сети, а следовательно и конечное время обучения, сравнительная простота аппаратной реализации.

Предпосылки создания бинарной матричной нейронной сети

Попытки создания искусственных нейронных сетей основываются на факте существования их естественных прототипов. Способ передачи и обработки информации в естественной нейронной сети определяется химико-биологическими свойствами живых клеток-нейронов. Однако, модель искусственной нейронной сети не обязана полностью копировать как функцию нейронов, так и структуру естественного мозга, так как реализует только функцию преобразования информационных входов в выходы. Поэтому реализация функции искусственной нейронной сети может значительно отличаться от ее естественного аналога. Попытка прямого копирования структуры естественного мозга неизбежно сталкивается со следующими проблемами, которые, при отсутствии их решения, могут оказаться непреодолимыми. Как известно, в мозге млекопитающих выход нейрона может быть подключен к входам нескольких других нейронов.

Как узнать входы каких нейронов должны быть связаны с выходами других нейронов? Сколько нейронов должно быть связано с каждым конкретным нейроном в сети для того чтобы сеть выполняла свою функцию?

Ответов на эти вопросы пока нет, а подключение нейронов друг к другу методом перебора гарантирует практически бесконечное время обучения такой сети, учитывая что количество нейронов реального мозга исчисляется миллиардами.

В искусственных нейронных сетях перцептронного типа все нейроны соседних слоев связаны друг с другом. А “сила” связи определяется значением коэффициентов. Связь “все-со-всеми”, это решение проблемы связей нейронов методом “грубой силы”. В этом случае, нейронная сеть может содержать только сравнительно небольшое число нейронов на промежуточных слоях для приемлемого времени обучения, например, в течение нескольких недель [2].

Прежде чем нейронная сеть станет выдавать результат, например, классифицировать изображения, она должна пройти этап обучения, то есть этап настройки. На этапе обучения как раз и определяются конфигурация взаимодействия и общая функция нейронов сети. По сути, обучить нейронную сеть означает подобрать функцию преобразования таким образом, чтобы на заданных входах она давала правильные выходы с заданным уровнем ошибки. Затем, после обучения, мы даем на вход сети произвольные данные, и надеемся, что функция нейронной сети подобрана достаточно точно и сеть станет правильно, с нашей точки зрения, классифицировать любые другие входные данные. В популярных сетях перцептронного типа структура сети задается изначально фиксированной, см. например [2], а функция находится подбором коэффициентов связей нейронов промежуточных слоев. Прежде чем переходить к описанию матрицы, заметим, что одновременную связь всех нейронов соседних слоев можно разложить в последовательные связи пар нейронов пользуясь тем что функция нейрона это линейная комбинация выходов нейронов предыдущего слоя и коэффициентов связи. То есть, по крайней мере, для сетей перцептронного типа, каждый нейрон можно представить как принимающий данные только от двух других нейронов.

Принцип разложения нескольких параллельных связей в последовательность пар или троек связей только соседних нейронов и лежит в основе матрицы описываемой ниже. Принимается ограничение, что вовсе не обязательно обучать сеть подключая к нейрону все остальные, достаточно ограничиться только соседними нейронами, а затем последовательно уменьшать ошибку функции обучения сети. Данная версия нейронной сети основывается на предыдущей работе автора [1].

Структура матрицы и нейрона

Следующая матричная структура нейронной сети позволяет решить проблему подключения нейронов и ограничить число комбинаций при поиске функции нейронной сети. Эта сеть также в теории позволяет найти функцию нейронной сети с нулевой ошибкой на обучающих наборах входов/выходов за счет того, что функция сети является дискретной векторной функцией нескольких переменных.

На рис.1 представлен пример бинарной матрицы. Входы и выходы этой матрицы — двоичные четырех-компонентные векторы. Входы подаются снизу, сверху получаем выходные значения. Каждая клетка матрицы это нейрон с двоичной функцией нескольких переменных f. Каждый нейрон имеет горизонтальную и вертикальную перегородки, отделяющие его от соседних нейронов и определяющие перетоки данных. Вертикальная перегородка нейрона, изображена слева от каждого нейрона, может иметь три положения: закрыто (темная полоса), открыта вправо (зеленая стрелка вправо), открыта влево (желтая стрелка влево).

Горизонтальная перегородка, изображена снизу от нейрона, может иметь два положения: закрыто «стоп» (темная полоса) или открыто вверх (зеленая стрелка). Таким образом, переток данных в матрице может быть снизу вверх и влево/вправо. Для того чтобы избежать выделения граничных разрядов данных первый и последний нейроны в каждом ряду логически зациклены, то есть, например, стрелка влево первого нейрона в ряду является входом последнего нейрона в этом же ряду, как показано на рис.1 для нейронов второго ряда.

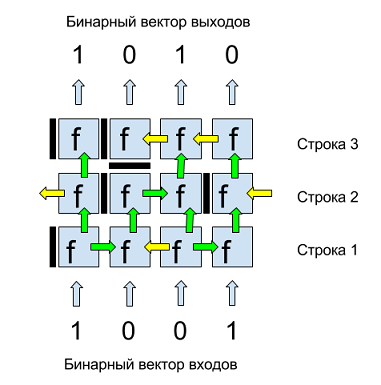
Рис. 1. Пример бинарной матрицы из 3-х строк и 4-х двоичных входов/выходов.

Структура матрицы подчиняется правилам поэтапного построения. Если данный набор строк нейронов не решает задачу, то к ним добавляются следующие, и так пока целевая функция не будет достигнута. Если приближение к результату не прослеживается в течение какого-то числа шагов, либо даже сама целевая функция меняется, например, при изменении обучающей выборки, то блок разрушается, так как целевая функция не может быть достигнута.

Перед обучением матрица состоит из одной первой строки. Обучение матрицы заключается в последовательном добавлении строк. Новые строки добавляются после нахождения одной или нескольких конфигураций перегородок на текущей строке, а также внутренних параметров нейронов, при которых значение ошибки на обучающих наборах матрицы минимально и меньше чем значение ошибки обучения на предыдущей строке.

Нейроны выполняют функцию преобразования данных, передачу или остановку сигнала. Функция нейрона f, в зависимости от текущей конфигурации перегородок и внутренних констант, должна удовлетворять следующим обязательным требованиям:

1. иметь возможность передачи данных без изменений;
2. уметь передавать константу (0 или 1) без входных данных;
3. не должна зависеть от последовательности применения входных данных от соседних нейронов, то есть нейрон выдает результирующее значение от всех своих входов поступивших как бы одновременно.

Один из вариантов такой функции f это сложение по модулю 2 или исключающее ИЛИ или XOR, как она часто обозначается в языках программирования.
Передача без изменения означает фактическое отсутствие нейрона и нужна только с точки зрения пропускания уровня матрицы без изменения данных.

Кроме обработки и передачи сигнала нейроны также имеют функцию памяти и ее использования или неиспользования в зависимости от функции реализуемой нейроном.
В зависимости от положения (значений) перегородок нейрона и его соседних нейронов, каждый нейрон может иметь от нуля до трех входов (снизу, справа и слева) и всегда один выход (вверх), который, однако, может быть не подключен к нейрону следующей строки, из за положения горизонтальной перегородки верхнего нейрона “стоп”.

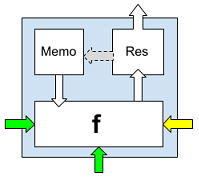
Рис. 2. Нейрон с бинарной функцией f, ячейкой памяти Memo и полем Res.

Каждый нейрон выполняет одну и ту же двоичную функцию f, которая отличается только количеством входных значений в зависимости от конфигурации перегородок нейрона, которые разрешают входные данные от нейрона предыдущей строки и двух боковых соседних нейронов, а также от бинарной внутренней константы Memo.

Нейрон получает данные на вход, выполняет двоичную функцию нейрона f на основе входов и поля Memo и помещает результат в поле Res. Варианты использования поля Memo могут быть различны. Если выход всей матрицы зависит только от входов сети, то поле Memo является частью конфигурации сети вместе со значениями перегородок нейронов. Если же сеть должна обучаться также и на основе предыдущих значений, то есть обладать памятью, например, для задач реализации искусственной жизни, то поле Memo может принимать вновь вычисленное значение Res как показано на рис. 2 пунктирной стрелкой.

Допустим что функция нейрона f это бинарная операция XOR применяемая последовательно ко всем входных параметрам. Проверим, что она отвечает трем необходимым требованиям.

1. Передача данных без изменений обеспечивается вариантом, изображенным на Рис. 3. Здесь Memo = 0, Горизонтальная нижняя перегородка в значении “вверх”, Левая и правая перегородки в значении “стоп”.

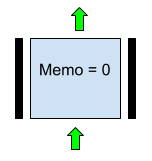
Рис. 3. Вариант параметров нейрона, реализующий передачу входа с предыдущей строки без изменения в случае f = XOR.

2. Передача константы обеспечивается значениями горизонтальной и вертикальных перегородок “стоп”, а значение Memo — это значение передаваемой константы.

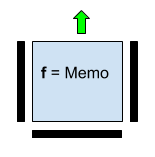
Рис. 4. Нейрон с функцией, передающей независимую бинарную константу Memo. Входные значения снизу, слева и справа не используются.

3. Требование независимости значения функции нейрона от последовательности обработки входных значений нейрона обеспечивается ассоциативностью XOR.

Число комбинаций полного перебора функций строки

Последовательное, построчное построение функции матрицы позволяет эффективно оптимизировать процесс обучения за счет замены полного перебора комбинаций бинарных функций всех нейронов матрицы полным перебором комбинаций функций нейронов строк. Одним из ключевых моментов в обучении сети является количество комбинаций полного перебора функций нейронов одной строки.

Для варианта нейрона описанного выше в переборе функций нейрона участвуют:

1. горизонтальная перегородка с двумя положениями: стоп и вверх;
2. вертикальная перегородка нейрона с тремя положениями: стоп, влево и вправо;
3. двоичное поле Memo со значениями 0 и 1.

Чтобы подсчитать число вариантов функций нейрона на основе комбинаций этих параметров перемножаем количество вариантов значений для каждого из этих параметров:

$inline$Q_n = 2times2times3=12$inline$. Таким образом, каждый нейрон, в зависимости от количества пришедших на вход параметров, может иметь один из 12 вариантов двоичной функции. Подсчитаем число вариантов полного перебора функций одной строки матрицы из 8 нейронов, которая, таким образом, может обрабатывать данные размером 1 байт: $inline$Q_s=12^8=429:981:696$inline$.

Для современного персонального компьютера это не очень большое число вычислений. При выборе функции нейрона c меньшим числом вариантов, например, без поля Memo, число комбинаций значительно уменьшается до $inline$6^8=1:679:616$inline$. Даже такая значительно упрощенная версия функции нейрона демонстрирует уменьшение ошибки обучения в процессе оптимизации. В программных тестах с разными вариантами нейронных функций на языке C# автору удавалось получить скорость перебора в диапазоне 200-600 тысяч вариантов в секунду, что дает полный перебор вариантов функций строки матрицы примерно за 3 секунды. Однако, это не означает, что например, матрица размером 8x8 будет обучена в течении 24 секунд. Дело в том, что возможно несколько комбинаций функций строки дающих одно и то же текущее минимальное значение ошибки обучения (метрики). Какая из этих, десятков, сотен или тысяч комбинаций приведет в итоге к нулевой ошибке обучения всей матрицы мы не знаем, и тогда в наихудшем случае нужно будет проверить каждую из них, что приводит к построению дерева оптимизационного поиска.

Естественным образом возникает вопрос, а какая двоичная функция нейрона f является наилучшей для обучения матрицы. Очевидно, что идеальной будет функция гарантирующая аналог функциональной полноты булевых функций [3] для строки матрицы в заданном наборе параметров перегородок и поля Memo. В этом случае мы будем иметь большую, если не полную, гарантию нахождения матрицы с нулевой ошибкой обучения. Однако, вопрос нахождения такой функции нейрона еще требует изучения.

Построение дерева оптимизации или поиска нуля ошибки обучения матрицы

Функцию ошибки обучения матрицы будем называть метрикой. Значение метрики показывает степень отклонения выхода матрицы от ожидаемого на обучающих данных.

Пример метрики. Предположим что входы и выходы матрицы это 4-х битные числа. И мы хотим обучить матрицу умножать входные числа на $inline$2$inline$. Допустим, что для обучения используется три входных значения $inline${1, 2, 3}$inline$, идеальный выход для которых будут числа $inline$R_1,R_2,R_3:{0001,0010,0011}$inline$.

Тогда входы обучения для матрицы будут четырех-битовые значения: $inline${0001, 0010, 0011}$inline$, а выходы, соответственно $inline${0001, 0100, 0110}$inline$, по одному биту на нейрон входной и выходной строк, соответственно.

На некоторой комбинации перегородок и полей Memo подставляем значения входов в матрицу и получаем выходы. Например, выходными значениями матрицы будут двоичные векторы $inline${0010, 0001, 1000}$inline$. Переводим их в десятичный вид $inline$r_1, r_2, r_3: {2, 1, 8}$inline$.

Получаем значение метрики для текущих выходов матрицы:
$inline$M=sumlimits_{i=1}^3{|R_i-r_i|}=|1-2|+|4-1|+|6-8|=6$inline$
В данном случае ошибка обучения равна 6 и задача найти такую конфигурацию нейронов на следующей строке матрицы, для которой значение метрики меньше $inline$6$inline$.
Рассмотрим один из вариантов поиска нуля метрики, при котором каждая новая строка матрицы добавляется к предыдущим строкам с конфигурацией перегородок и полей Memo, дающей минимальное значение метрики на обучающих данных.

Общий алгоритм построения дерева оптимизации матрицы.

1. Задаем начальное положительное  значение метрики, например max(Int32). Создаем матрицу, изначально состоящую из одной строки с начальными значениями перегородок "стоп" и нулевыми константами Memo.

2. Цикл: для каждой конфигурации перегородок и констант нейронов первой строки вычисляем значение метрики по всему обучающему набору данных.

     a. Если значение метрики меньше ее текущего минимального значения, то запоминаем новое минимальное значение, а матрицу заносим в список поиска как точку ветвления, предварительно очистив этот список.
     b. Если значение метрики равно текущему, то заносим текущую конфигурацию матрицы в список поиска как точку ветвления.
     c. Если значение метрики больше текущего минимального, то матрица отбрасывается, берем следующую комбинацию и идем на начало цикла.
     d. Если значение метрики равно нулю, то поиск закончен и найден один (из нескольких возможных) вариант обученной матрицы.

3. После перебора всех комбинаций функций на первой строке берем последовательно матрицы из списка поиска на первой строке, добавляем к ним строку и для каждой из этих матриц применяем алгоритм поиска.

Детали этого алгоритма могут быть различны, как в плане экономии памяти, так и ускорения скорости работы, например, сортировкой списков за счет особенностей конфигураций перегородок нейронов матриц или отбрасывания предыдущих списков ветвлений в соответствии с уменьшением текущего значения метрики.

Заключение

Практические эксперименты показывают что алгоритм обучения матрицы в большинстве случаев сходится. Например, в одном из тестов с функцией нейрона XOR, матрица шириной 8 битов научилась умножать на 2 числа от 1 до 6 с нулевой ошибкой обучения. Подставив на вход 7, на выходе получил 14, значит матрица научилась экстраполировать на один ход вперед, но уже на числе 8 матрица дала неправильный результат. Все обучение заняло несколько минут на домашнем персональном компьютере. Однако эксперименты с более сложными обучающими выборками требуют иных вычислительных мощностей.

Кроме передачи данных снизу вверх, можно также рассмотреть и обратные потоки, когда некоторые нейроны в текущей конфигурации матрицы передают результаты на предыдущие строки. С одной стороны, такие конфигурации могут давать необычные функции матрицы, включая циркулирующие данные, но, с другой стороны, увеличивают время обучения матрицы, так как добавляют еще один параметр конфигурации при переборе вариантов решения.
От плоских нейронов можно перейти к трехмерным, т.е. рассматривать их не как квадратные элементы, а как кубики, каждая грань которых получает или передает данные, и тогда (пока теоретически) можно получить вполне осязаемый трехмерный искусственный мозг.

Ссылки

1. A.V. Kazantsev, VISUAL DATA PROCESSING AND ACTION CONTROL USING BINARY NEURAL NETWORK — IEEE Eighth International Workshop (WIAMIS '07) Image Analysis for Multimedia Interactive Services, 2007.
2. Наталья Ефремова, Нейронные сети: практическое применение (habrahabr.ru)
3. Функциональная полнота булевых функций (Wikipedia)

Автор: Александр Казанцев

Источник