Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки

в 4:45, , рубрики: Научно-популярное, пилотаж, робототехника

Продолжаем серию статей по автоматизации выполнения фигур пилотажа на малом ДПЛА. Настоящая статья имеет, прежде всего, образовательную цель: здесь мы покажем, как можно создать простейшую систему автоматического управления (САУ) на примере задачи выполнения фигуры пилотажа «бочка» при управлении летательным аппаратом только элеронами. Статья является второй в цикле публикаций «Пилотажный ДПЛА», рассказывающем о процессе постройки аппаратной и программной частей САУ в обучающей форме.
Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 1

Ссылка на предыдущую статью цикла:
1. «Пилотажный ДПЛА. Как правильно сделать бочку»

Содержание:

  Введение
  Модель движения
  Параметры модели. Момент инерции
  Параметры модели. Производные момента крена
  Верификация модели
  Синтез управления для выполнения «бочки»
  Лётный эксперимент
  Замечания
  Выводы

Введение

Итак, мы решили реализовать «бочку» в автоматическом режиме. Очевидно, что для автоматического выполнения фигуры необходимо сформулировать соответствующий закон управления. Процесс придумывания будет гораздо безболезненнее и быстрее, если использовать математическую модель движения ЛА. Проверка закона управления в лётном эксперименте хоть и возможна, но требует гораздо большего времени, к тому же может оказаться гораздо дороже в случае потери или повреждения аппарата.
Так как при небольших углах атаки и скольжения самолёта его движение по крену практически не связано с движением в двух других каналах: путевом и продольном — для выполнения простой «бочки» достаточно будет построить модель движения только вокруг одной оси — оси ОХ связанной СК. По этой же причине, закон управления элеронами не будет существенно изменяться, когда дело дойдет до создания полной системы управления.

Модель движения

Уравнение движения ЛА вокруг продольной оси ОХ связанной СК крайне простое:

$I_{x}dot{mathrm{omega}}_x=M_x,$

где $I_x$ — момент инерции относительно оси ОХ, а момент $M_x$ состоит из нескольких составляющих, из которых для реалистичного описания движения нашего самолёта достаточно рассмотреть только две:

$M_x=M_x^{omega_x}omega_x+M_x^{delta_a}delta_a,$

где $M_x^{omega_x}omega_x$ — момент, обусловленный вращением ЛА вокруг оси ОХ (демпфирующий момент), $M_x^{delta_a}delta_a$ — момент, обусловленный отклонением элеронов (управляющий момент). Последнее выражение записано в линеаризованной форме: момент тангажа $M_x$ линейно зависит от угловой скорости $omega_x$ и угла отклонения элеронов $delta_a$ с постоянными коэффициентами пропорциональности $M_x^{omega_x}$ и $M_x^{delta_a}$ соответственно.

Как известно (например, из Вики), линейному дифференциальному уравнению

$I_{x}dot{mathrm{omega}}_x=M_x^{omega_x}omega_x+M_x^{delta_a}delta_a$

соответствует апериодическое звено первого порядка

$W=frac {k}{Tp+1},$

где $W$ — передаточная функция, $p$ — оператор дифференцирования, $T$ — постоянная времени, а $k$ — коэффициент усиления.

Как перейти от дифференциального уравнения к передаточной функции?

В нашем случае от параметров уравнения к параметрам передаточной функции можно перейти следующим образом (зная, что производная $M_x^{omega_x}$ отрицательная):

$I_xdot{omega}_x=M_x^{omega_x}omega_x+M_x^{delta_a}delta_a longrightarrow I_xdot{omega}_x=-left | M_x^{omega_x}right | omega_x+M_x^{delta_a}delta_a $

$I_xdot{omega}_x+left | M_x^{omega_x}right | omega_x=M_x^{delta_a}delta_a longrightarrow left( I_xp+left | M_x^{omega_x}right | right)omega_x=M_x^{delta_a}delta_a$

$ left( frac{I_x}{left | M_x^{omega_x}right |}p + 1 right) omega_x=frac{M_x^{delta_a}}{left | M_x^{omega_x}right |}delta_alongrightarrow T=frac{I_x}{left | M_x^{omega_x}right |}, k=frac{M_x^{delta_a}}{left | M_x^{omega_x}right |}.$

Для апериодического звена постоянная времени $T$ равна времени, за которое выходная величина $omega_x(t)$ при единичном ступенчатом воздействии входной величины $delta_a(t)$ принимает значение, отличающееся от установившегося на величину ~5%, а коэффициент усиления $k$ численно равен установившемуся значению выходной величины при единичном ступенчатом воздействии:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 27

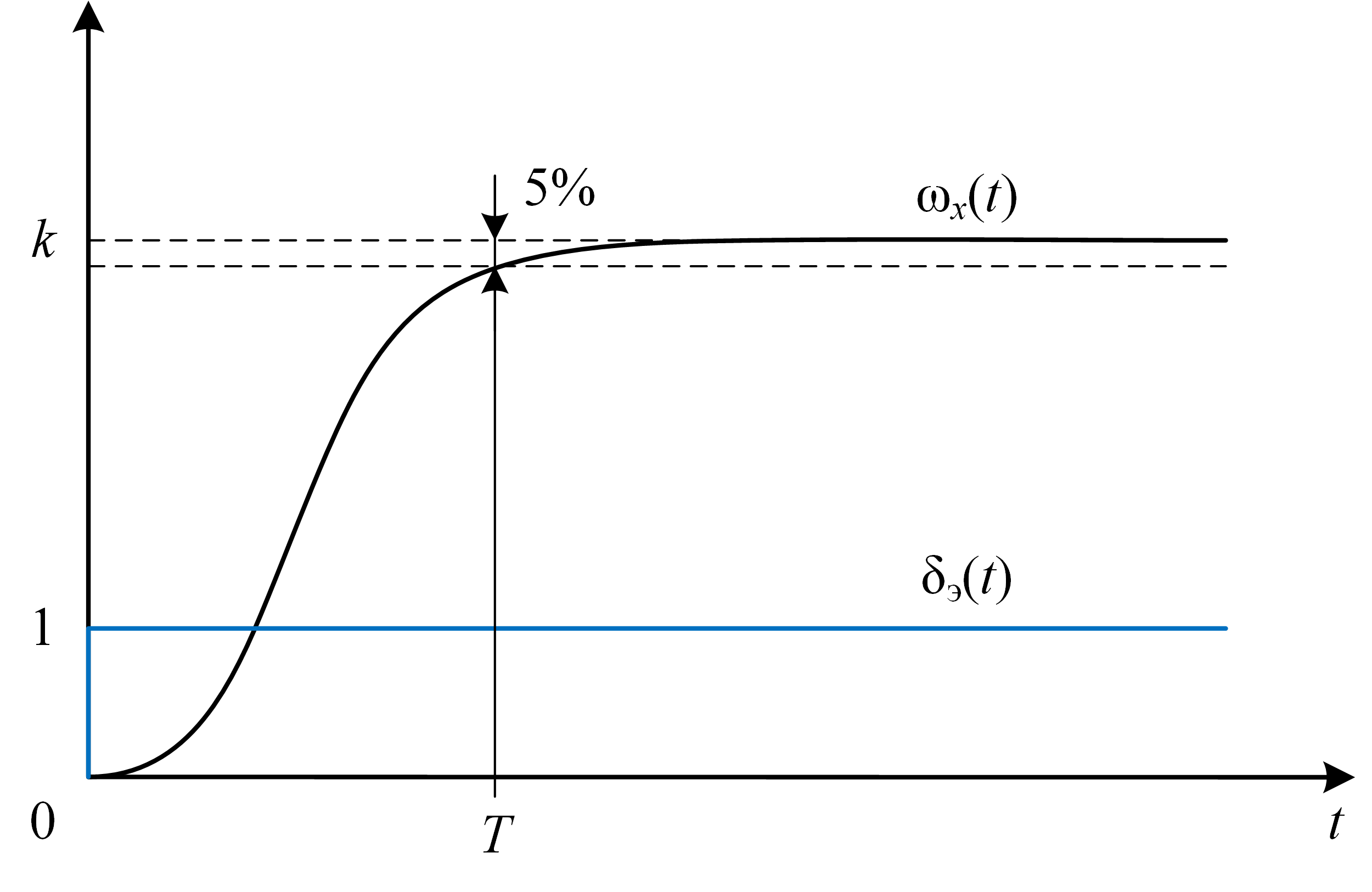
В построенной модели движения есть два неизвестных параметра: коэффициент усиления $k$ и постоянная времени $T$. Эти параметры выражаются через характеристики физической системы: момент инерции $I_x$, а также производные момента тангажа $M_x^{omega_x}$ и $M_x^{delta_a}$:

$M_x^{omega_x}=-frac{I_x}{T}, {color{white} longrightarrow} M_x^{delta_a}=-kM_x^{omega_x}=frac{kI_x}{T}.$

Таким образом, если известен момент инерции $I_x$, то, определив параметры модели, по ним можно восстановить параметры системы.

Параметры модели. Момент инерции $I_x$

Наш летательный аппарат состоит из следующих частей: крыло, фюзеляж с оперением, двигатель, аккумулятор (АКБ) и БРЭО:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 36

К БРЭО относятся: плата автопилота, плата приёмника СНС, плата радиомодема, плата приёмника сигнала от управляющей аппаратуры, два регулятора напряжения, регулятор оборотов двигателя, а также соединительные провода.

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 37

В силу малого веса БРЭО, его вкладом в общий момент инерции можно пренебречь.

Как проводилась оценка величины момента инерции?

Оценку момента инерции $I_x$ можно провести следующим образом. Посмотрим на самолёт вдоль оси ОХ:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 39

А затем представим его в виде следующей упрощённой модели:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 40
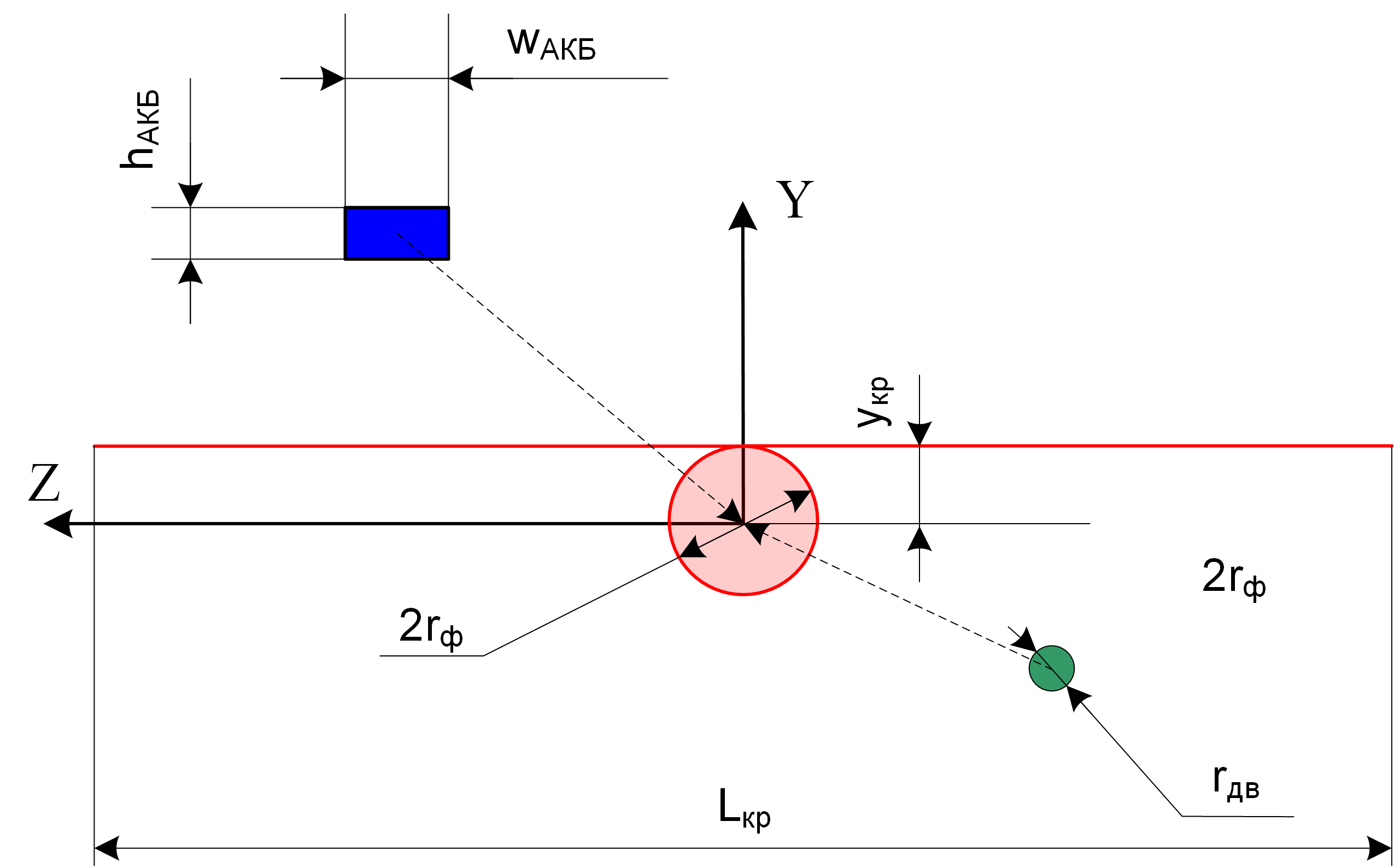
Схема для расчёта момента инерции $I_x$. Слева вверху — аккумулятор, справа внизу — двигатель. Двигатель и аккумулятор располагаются на оси фюзеляжа

Видно, что для создания модели были отброшены: киль, горизонтальное оперение, винт, а также БРЭО. При этом остались: фюзеляж, крыло, аккумулятор, двигатель. Измерив массы и характерные размеры каждой части, можно вычислить моменты инерции каждой части относительно продольной оси фюзеляжа:

  • крыло (тонкий стержень): $I_{x w}=frac{1}{12}m_{w}L_{w}^2+m_{w}y_{w}^2=1.7cdot10^{-2} kgcdot m^{2}$
  • фюзеляж (полый цилиндр): $I_{x f}=m_{f}r_{f}^2=2.8cdot10^{-4} kgcdot m^{2}$
  • аккумулятор (пластина): $I_{x a}=frac{1}{12}m_{a}left (h_{a}^2+w_{a}^2right )=3.4cdot10^{-4} kgcdot m^{2}$
  • двигатель (диск): $I_{x e}=frac{1}{2}m_{e}r_{e}^2=2.3cdot10^{-5} kgcdot m^{2}$

Общее значение момента инерции ЛА относительно оси ОХ получим сложением моментов инерции частей:

$I_x=I_{x w}+I_{x f}+I_{x a}+I_{x e}=1.8cdot10^{-2} kgcdot m^{2}$

Оценив вклад каждой из частей ЛА в общий момент инерции $I_x$, получилось следующее:

  • крыло — 96.3%,
  • фюзеляж — 1.6 %,
  • двигатель и аккумулятор — 2%,

Видно, что основной вклад в общий момент инерции $I_x$ вносит крыло. Это связано с тем, что крыло имеет довольно большой поперечный размер (размах крыла — 1 м):

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 49

Поэтому, несмотря на скромный вес (около 20% от общей взлётной массы ЛА), крыло имеет значительный момент инерции.

Параметры модели. Производные момента крена $M_x^{omega_x}$ и $M_x^{delta_a}$

Вычисление производных момента крена – довольно трудная задача, связанная с расчётом аэродинамических характеристик ЛА численными методами или с помощью инженерных методик. Применение первых и вторых требует значительных временных, интеллектуальных и вычислительных затрат, которые оправданы при разработке систем управления большими самолётами, где стоимость ошибки всё же превышает затраты на построение хорошей модели. Для задачи управления БПЛА, масса которого не превосходит 2 кг, такой подход вряд ли оправдан. Другой способ вычисления этих производных — лётный эксперимент. Учитывая дешевизну нашего самолёта, а также близость подходящего поля для проведения такого эксперимента, для нас выбор был очевиден.
Записав в автопилот прошивку для ручного управления и регистрации параметров, мы собрали самолёт и подготовили его к испытаниям:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 52

В лётном эксперименте удалось получить данные по углу отклонения элеронов и угловой скорости вращения ЛА. Пилот управлял самолётом в ручном режиме, выполняя полёт по кругу, развороты и «бочки», а бортовое оборудование регистрировало и отправляло необходимую информацию на наземную станцию. В результате были получены необходимые зависимости: $omega_x(t)$ (град/с) и $delta_a(t)$ (б/р). Величина $delta_a(t)$ представляет собой нормированный угол отклонения элеронов: значение 1 соответствует максимальному отклонению, а значение −1 — минимальному:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 56

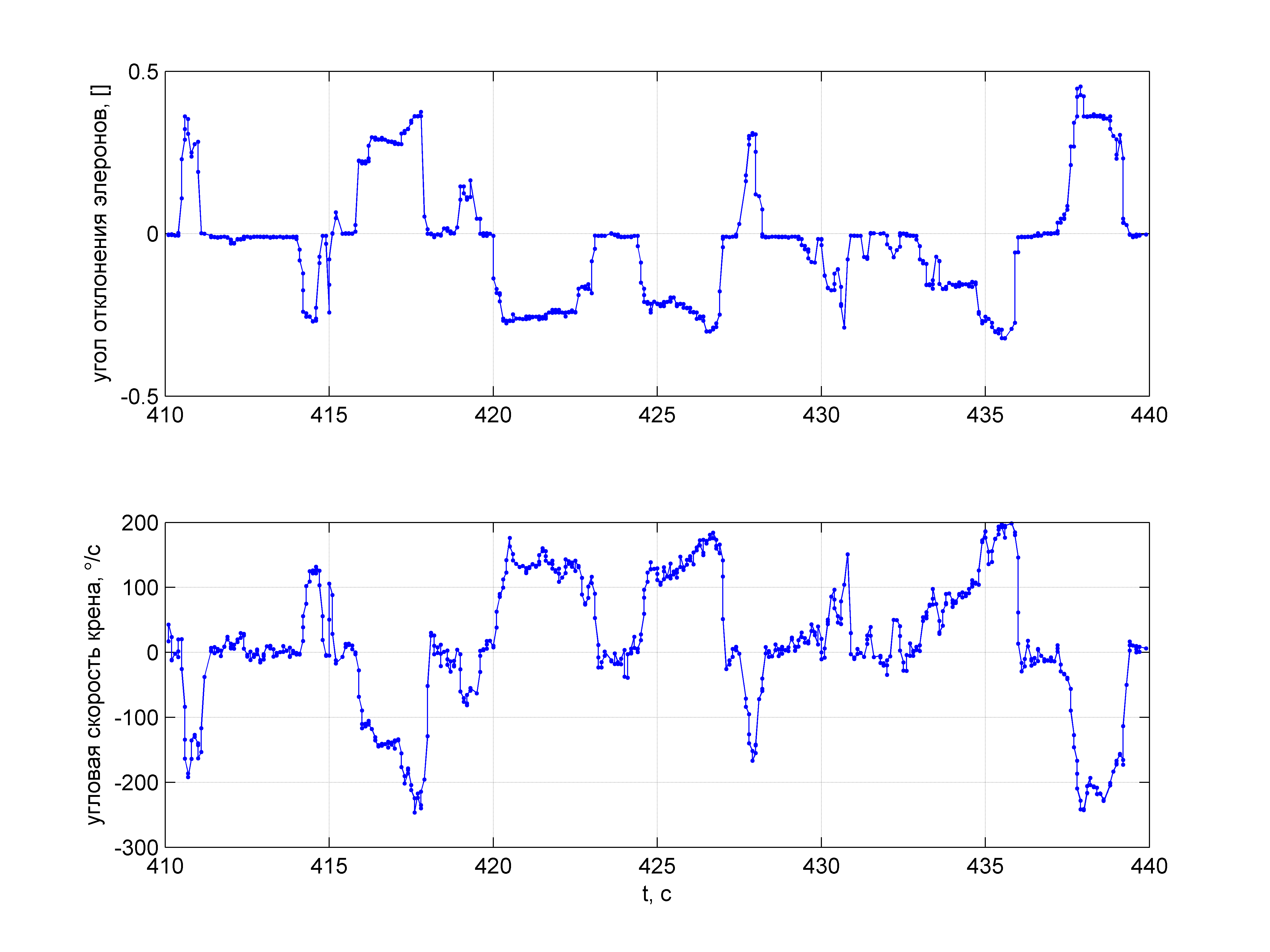
Как теперь определить $M_x^{omega_x}$ и $M_x^{delta_a}$ из полученных данных? Ответ — измерить параметры переходного процесса по графикам $omega_x(t)$ и $delta_a(t)$.

Как определялись коэффициенты k и T?

Коэффициент усиления $k$ определялся путём отнесения величины установившегося значения угловой скорости к величине отклонения элерона:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 62
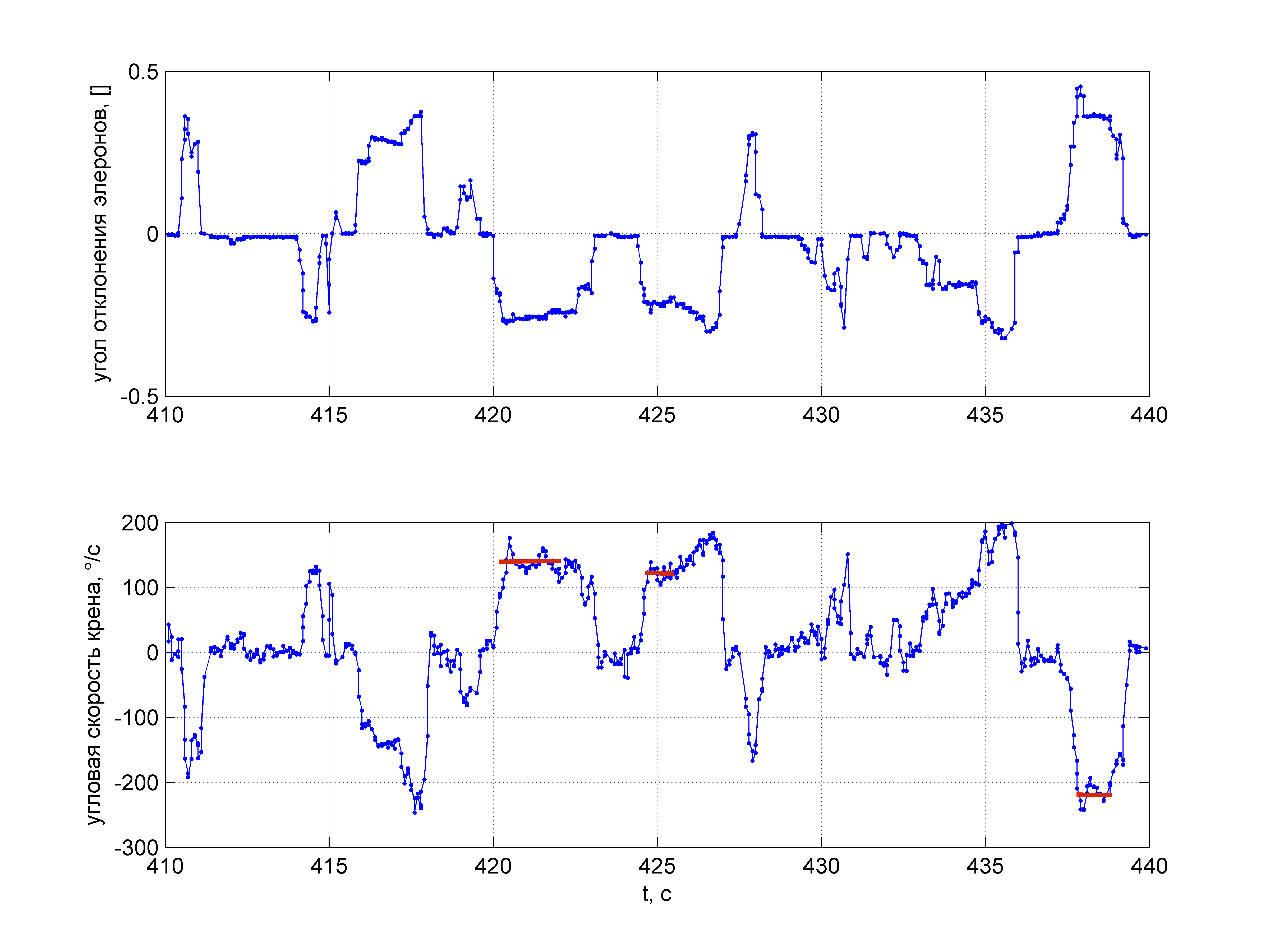
Зависимости угла отклонения элеронов и угловой скорости крена от времени, полученные в лётном эксперименте

На предыдущем рисунке участкам установившегося значения угловой скорости приблизительно соответствуют, например, отрезки вблизи моментов времени 422, 425 и 438 с (отмечены тёмно-красным на рисунке).
Постоянная времени $T$ определялась из тех же графиков. Для этого найдены участки резкого изменения угла отклонения элерона, а затем измерено время, за которое угловая скорость принимает значение, отличающееся от установившегося значения на 5%.

Результат определения значений постоянной времени и коэффициента усиления следующий: $T=0.075 text{ s}$, $k=-575 text{ deg/s}$. Этим значениям коэффициентов при известном значении момента инерции $I_x$ соответствуют следующие значения производных момента тангажа:

$M_x^{omega_x}=-frac{I_x}{T}=-0.24frac{text{N}cdottext{m}}{text{deg/s}}, {color{white} longrightarrow} M_x^{delta_a}=-kM_x^{omega_x}=frac{kI_x}{T}=-138frac{text{N}cdottext{m}}{text{[ ]}}.$

Верификация модели

Итак, построив модель, основой которой является апериодическое звено

$W=frac {-575}{0.75p+1},$

можно провести её верификацию, подав на вход сигнал $deltaэ(t)$, полученный из лётного эксперимента, и сравнить выходной сигнал модели с величиной $omega_x(t)$, также полученной в эксперименте.

Как проводилось моделирование?

Инструмент для проведения моделирования мы выбирали, прежде всего, основываясь на возможности повторения результатов широким кругом читателей: это прежде всего означает, что программа должна быть в общественном доступе. В принципе задачу моделирования поведения апериодического звена первого порядка можно решить и создав свой собственный инструмент с нуля. Но так как в дальнейшем модель будет усложняться, то создание своего инструмента может отвлечь от основной задачи — создания САУ пилотажного ДПЛА. С учётом принципа открытости инструмента мы выбрали JSBsim.

В предыдущем разделе мы получили значения коэффициентов $M_x^{delta_a}$ и $M_x^{omega_x}$. Используем их для моделирования движения самолета. Из прошлой статьи мы помним, что конфигурация модели самолета в JSBsim задается при помощи XML файла. Создадим собственную модель:

<?xml version="1.0"?>
<fdm_config name="OP1" version="2.0" release="BETA">

    <metrics>
        <wingarea unit="M2"> 0.2 </wingarea>
        <wingspan unit="M"> 1.0	</wingspan>
        <chord unit="M"> 0.2 </chord>
        <htailarea unit="M2"> 0.03 </htailarea>
        <htailarm unit="M"> 0.5 </htailarm>
        <vtailarea unit="M2"> 0.03 </vtailarea>
        <vtailarm unit="M"> 0.5 </vtailarm>
        <location name="AERORP" unit="M">
            <x> -0.025 </x>
            <y> 0 </y>
            <z> 0.05 </z>
        </location>
    </metrics>

    <mass_balance>
        <ixx unit="KG*M2"> 0.018 </ixx>
        <iyy unit="KG*M2"> 0.018 </iyy>
        <izz unit="KG*M2"> 0.018 </izz>
        <emptywt unit="KG"> 1.2 </emptywt>
        <location name="CG" unit="M">
            <x> 0 </x>
            <y> 0 </y>
            <z> 0 </z>
        </location>
    </mass_balance>

    <ground_reactions>
    </ground_reactions>
    <propulsion>
    </propulsion>
    <flight_control name="FCS: OP1">

	<channel name="Pitch">
        </channel>
		
        <channel name="Roll">
            <summer name="Roll Trim Sum">
                <input>fcs/aileron-cmd-norm</input>
                <clipto>
                    <min>-1</min>
                    <max>1</max>
                </clipto>
            </summer>
        </channel>
		
        <channel name="Yaw">
        </channel>
 
    </flight_control>

    <aerodynamics>

        <axis name="DRAG">
        </axis>

        <axis name="SIDE">
        </axis>

        <axis name="LIFT">
        </axis>

        <axis name="ROLL" unit="N*M">
            <function name="aero/coefficient/Clp">
                <description>Roll_moment_due_to_roll_rate</description>
                <product>
                    <property>velocities/p-aero-rad_sec</property>
                    <value>-0.24</value>
                </product>
            </function>
            <function name="aero/coefficient/Clda">
                <description>Roll_moment_due_to_aileron</description>
                <product>
			<property>fcs/aileron-cmd-norm</property>
			<value> 2.4 </value>
                </product>
            </function>
        </axis>

        <axis name="PITCH">
        </axis>

        <axis name="YAW">
        </axis>
    </aerodynamics>
	
 <output name="OP1.csv" rate="60" type="CSV">
        <property> velocities/vc-kts </property>
        <property> aero/alphadot-deg_sec </property>
        <property> aero/betadot-deg_sec  </property>
        <property> fcs/throttle-cmd-norm </property>

      <simulation>       OFF </simulation>
      <atmosphere>       OFF </atmosphere>
      <massprops>        OFF </massprops>
      <aerosurfaces>     ON  </aerosurfaces>
      <rates>            ON  </rates>
      <velocities>       ON  </velocities>
      <forces>           OFF </forces>
      <moments>          OFF </moments>
      <position>         ON  </position>
      <coefficients>     OFF </coefficients>
      <ground_reactions> OFF </ground_reactions>
      <fcs>              ON  </fcs>
      <propulsion>       OFF </propulsion>
    </output>	
		
</fdm_config>

Так как мы строим модель движения аппарата только по крену, оставим многие из секций файла пустыми. В файле модели последовательно задаются следующие характеристики.

Геометрические размеры самолёта задаются в секции metrics: площадь крыла, размах, длина средней аэродинамической хорды, площадь горизонтального оперения, плечо горизонтального оперения, площадь вертикального оперения, плечо вертикального оперения, положение аэродинамического фокуса.

Массовые характеристики самолёта задаются в секции mass_balance: тензор инерции самолета, вес пустого самолета, положение центра масс.

Стоит отметить, что абсолютные положения аэродинамического фокуса и центра масс самолета не участвуют в расчете динамики аппарата, важно их относительное расположение.
Далее следуют секции, описывающие характеристики шасси самолета и его силовой установки.

В следующей секции, ответственной за систему управления, заполним канал, ответственный за управление по крену: укажем единственный вход fcs/aileron-cmd-norm, величина которого будет нормирована от -1 до 1.

Аэродинамические характеристики задаются в секции aerodynamics: силы задаются в скоростной системе координат, моменты — в связанной. Нас интересует момент по крену. В секции axis name=«ROLL» задаются функции, которые определяют момент сил от различных составляющих проекции момента аэродинамических сил на ось OX связанной системы координат. В нашей модели таких составляющих две. Первая составляющая — демпфирующий момент, который равен произведению угловой скорости на определенный ранее коэффициент $M_x^{omega_x}$. Вторая составляющая — это момент от элеронов при фиксированной скорости полёта: он равен произведению ранее определенного коэффициента $M_x^{delta_a}$ на величину отклонения элеронов.

Стоит отметить, что при определении коэффициента $M_x^{delta_a}$ была использована размерная величина $T$. В наших полетных данные величина угловой скорости измерялась в градусах в секунду, тогда как в JSBSim используются радианы в секунду, поэтому коэффициент $M_x^{delta_a}$ должен быть приведен к нужной нам размерности, т. е. разделен на 180 градусов и умножен на $pi$ радиан. Записываем эти составляющие момента аэродинамических сил внутри функций произведения product. При моделировании результат выполнения всех функций суммируется и получается значение проекции аэродинамического момента на соответствующую ось.

Проверить созданную модель можно на экспериментальных данных, полученных при лётных испытаниях. Для этого создаем скрипт следующего содержания:

<?xml version="1.0" encoding="utf-8"?>
<runscript>

 <use aircraft="ownPlane1" initialize="scripts/airborne"/>
 <run start="0" end="51" dt="0.01">

<event name="Trims">
 <condition> sim-time-sec ge 0.0 </condition>
 <set name="simulation/do_simple_trim" value="5"/>  	
</event>

<event name="Time Notif" continuous="true">
 <description>Provide a time history input for the aileron</description>
 <condition> sim-time-sec ge 0</condition>
 <set name="fcs/aileron-cmd-norm" >
  <function>
   <table>
	<independentVar lookup="row">sim-time-sec</independentVar>
	<tableData>
0	0.00075
0.1	0.00374
0.2	-0.00075
0.3	-0.00075
0.4	-0.00075
0.5	-0.00075
0.6	0.00075
0.7	0.00075
...
48.8	-0.00075
48.9	0.00000
49	-0.00075

	</tableData>
    </table>
   </function>
 </set>
</event>		
</run>
</runscript>

где точками обозначены пропущенные данные. В знакомом нам по предыдущей статье файле скрипта появился новый тип события («Time Notif»), который позволяет задавать непрерывное изменение параметра по времени. Зависимость параметра от времени задана табличной функцией. JSBSim линейно интерполирует значение функции между табличными данными. Процедура верификации модели движения по крену заключается в исполнении данного скрипта на созданной модели и сравнения результатов с экспериментальными.

Результат верификации показан на рисунке:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 79

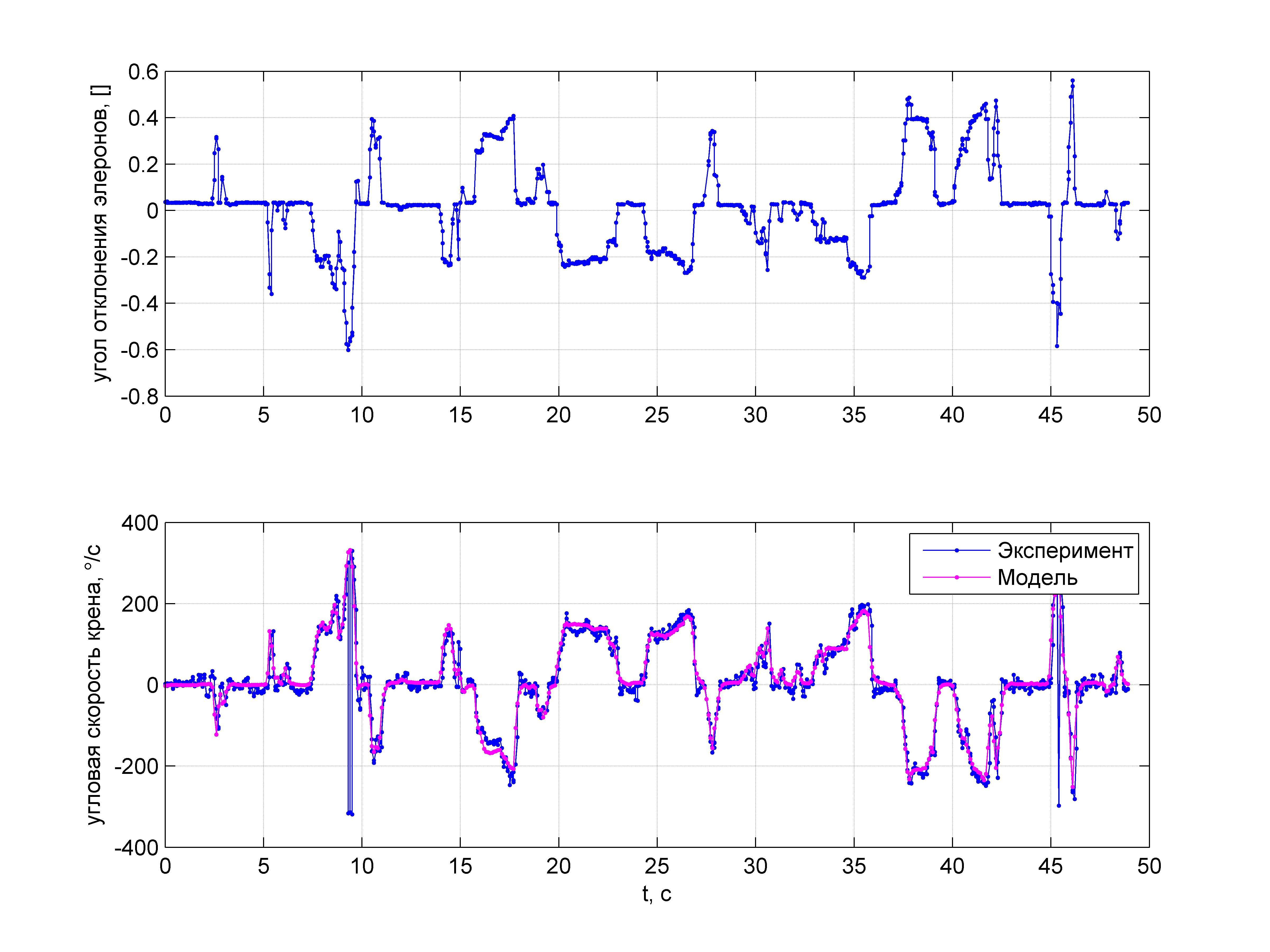
Как видно из рисунка, совпадение модели с реальностью чуть менее, чем полное.

Синтез управления для выполнения «бочки»

Получив модель, несложно определить, на какую величину и как долго необходимо отклонять элероны, чтобы выполнить «бочку». Одним из вариантов является следующий алгоритм отклонения:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 80
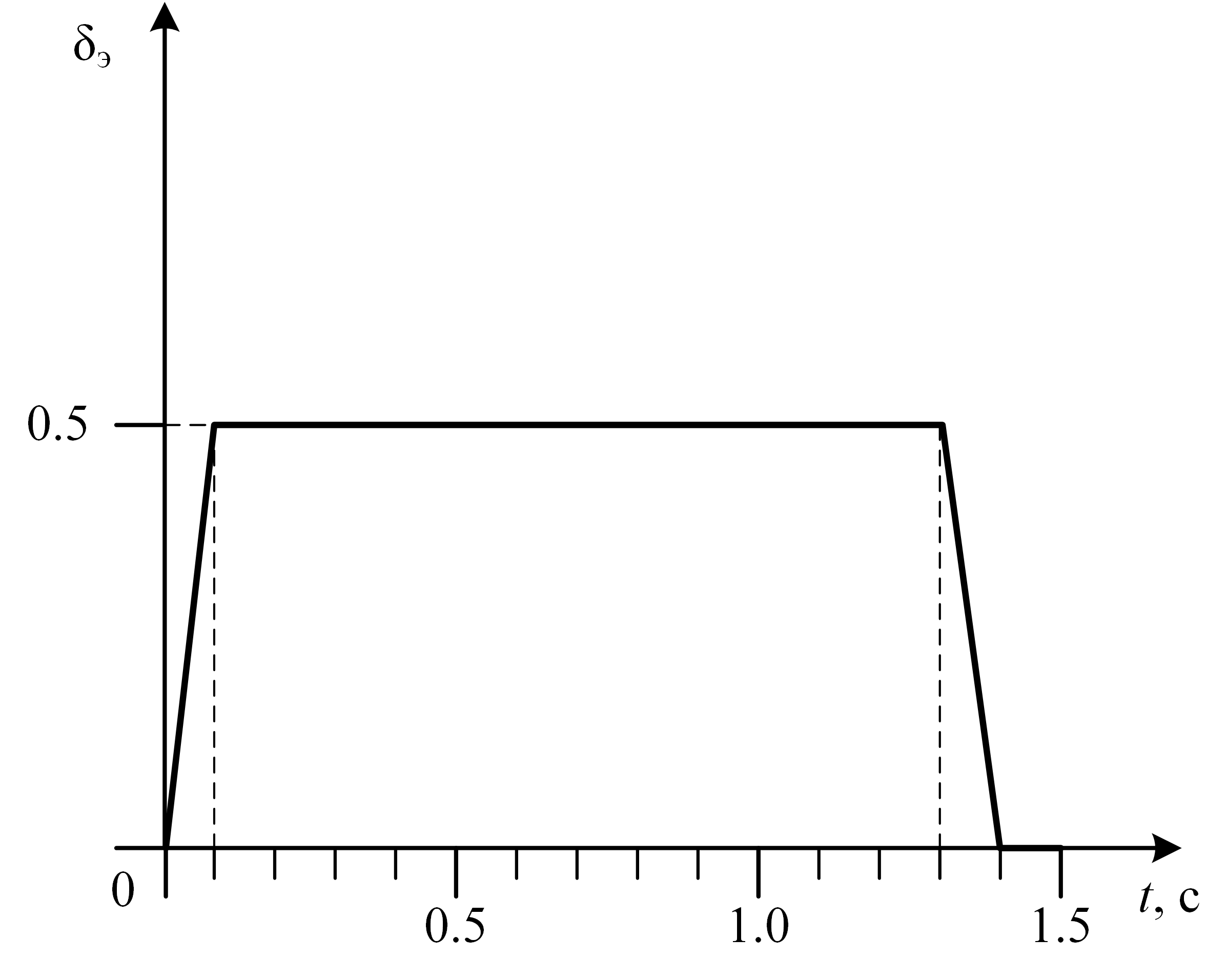
  • $t=0$: элероны начинают отклоняться из нейтрального положения;
  • $t=0.1text{ с}$: элероны отклонены на 50%;
  • $t=1.3text{ с}$: элероны начинают отклоняться в нейтральное положение;
  • $t=1.4text{ с}$: элероны в нейтральном положении.

Наличие отрезков длительностью по 0.1 с в начале и в конце алгоритма отклонения элеронов моделирует инертность сервопривода, который не может отклонить поверхности мгновенно. Модель показывает, что при таком законе отклонения элеронов ЛА должен выполнить один полный оборот вокруг оси ОХ, проверим?

Лётный эксперимент

Полученный закон управления элеронами был запрограммирован в автопилот, установленный на самолёт. Идея эксперимента проста: вывести самолёт в горизонтальный полёт, после чего задействовать полученный закон управления. В случае если реальное движение ЛА по крену соответствует созданной модели, то самолёт должен выполнить «бочку» — один полный оборот на 360 градусов.

Отдельно выражаем благодарность нашему верному пилоту за труд, профессионализм и удобный багажник на приоре-универсал!

В процессе проведения эксперимента стало ясно, что модель движения по крену была построена удачно — самолёт выполнял одну «бочку» за другой, как только пилот задействовал запрограммированный закон управления. На следующем рисунке показана угловая скорость $omega_x$, записанная в процессе эксперимента, и полученная по результатам моделирования, а также угол крена и тангажа из лётного эксперимента:

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 86

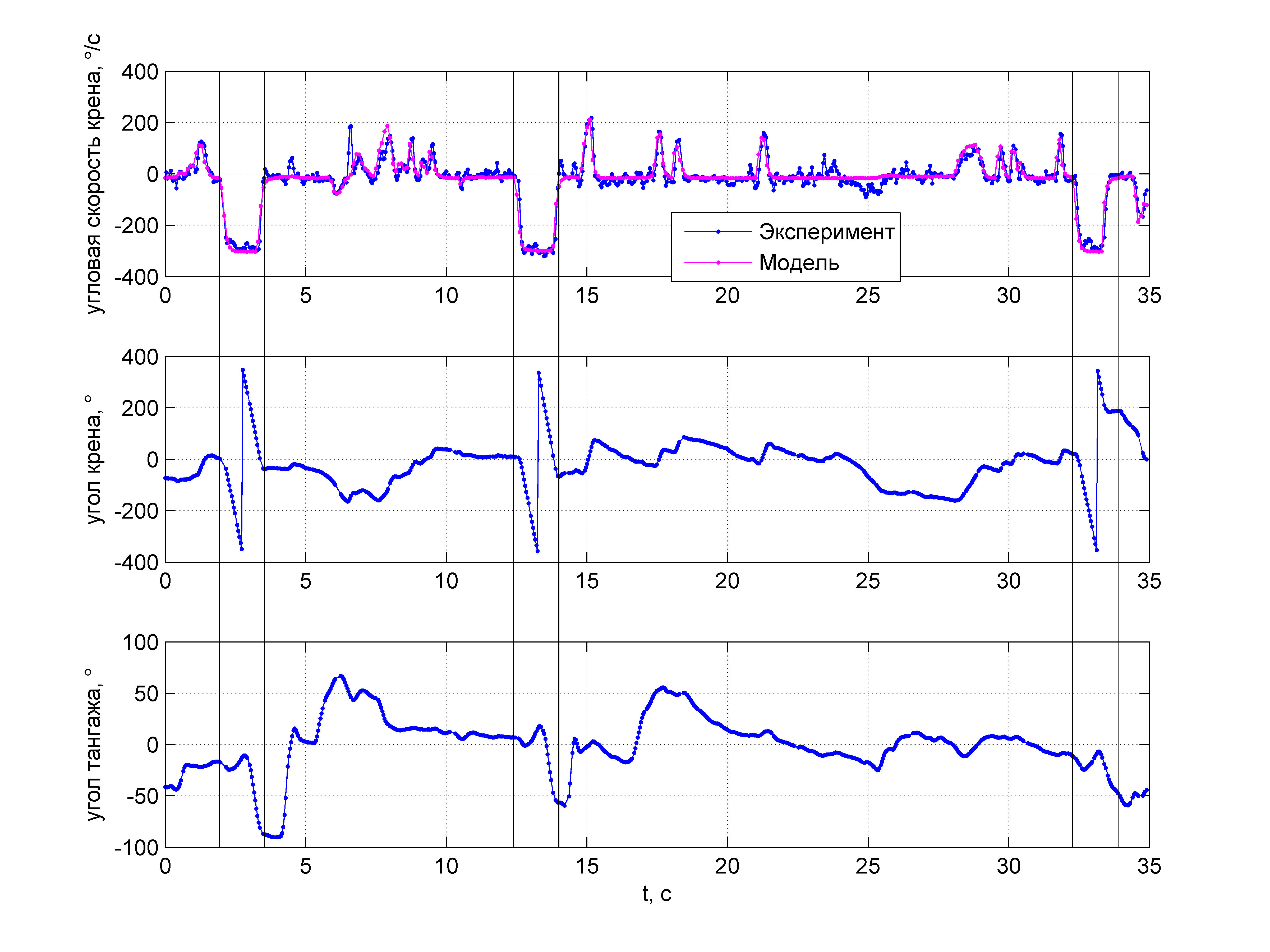
А на следующем рисунке показаны зарегистрированные в лётном эксперименте сигналы на элероны, руль высоты (РВ) и руль направления (РН):

Пилотажный ДПЛА. Часть 2. Простейшая модель движения для выполнения бочки - 87

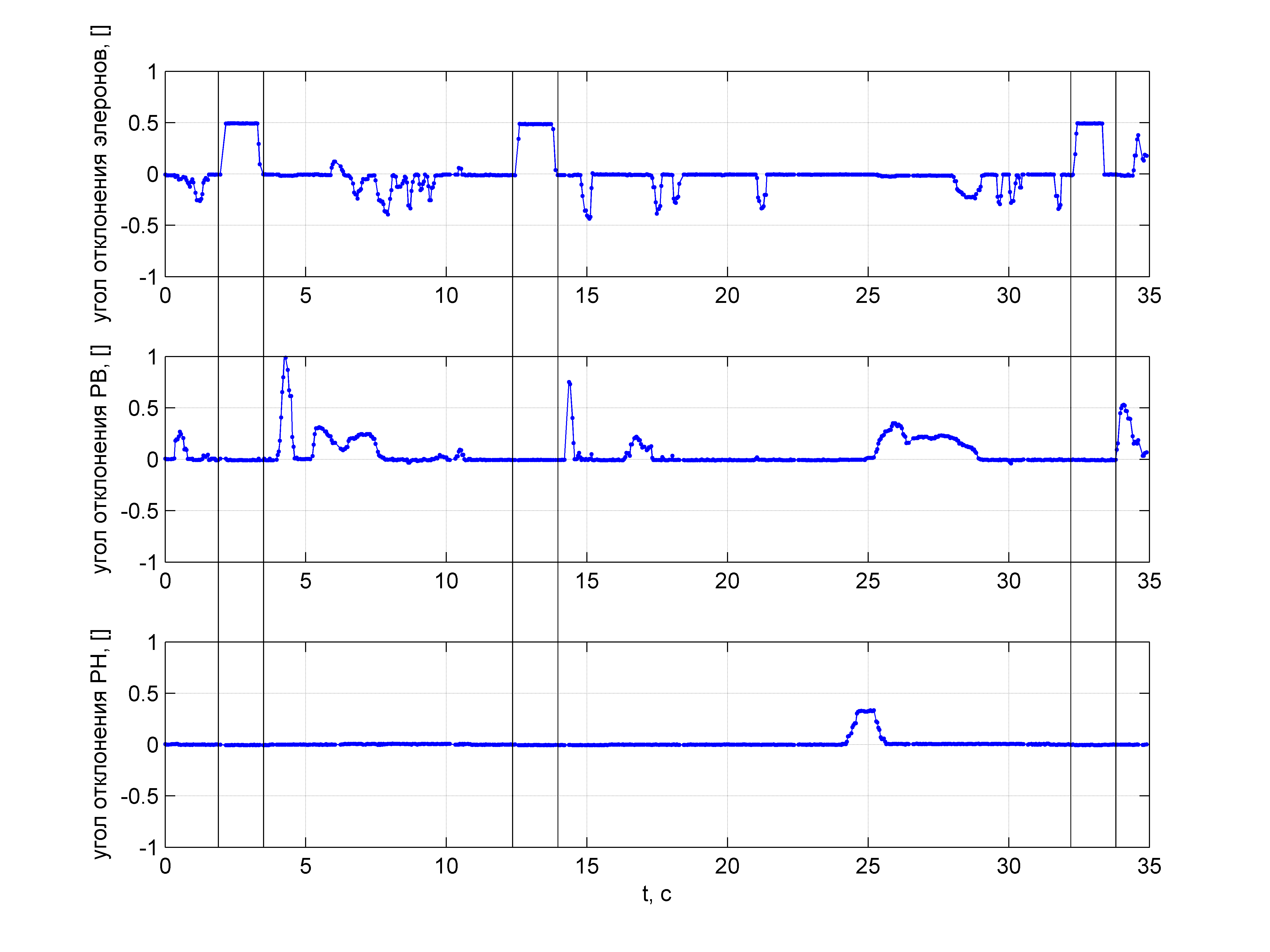
Вертикальными линиями обозначены моменты начала и окончания выполнения «бочки». Из рисунков видно, что в процессе выполнения «бочки» пилот не вмешивается в управление рулём высоты и рулём направления, также видно, что угол тангажа неизменно стремится уменьшиться при выполнении «бочки» — самолёт затягивает в пикирование, как это и было предсказано по результатам моделирования в авиасимуляторе (см. статью «Пилотажный ДПЛА. Как правильно сделать бочку»). Если внимательно рассмотреть предыдущие графики, то станет видно, что третья «бочка» даже не была закончена, потому что пилот вмешался в управление, чтобы вывести самолёт из пикирования: настолько сильно изменяется угол тангажа при выполнении «бочки» одними элеронами.

Замечания

  • Построенная САУ для выполнения «бочки» не учитывает зависимости производных момента крена от скорости полёта. С одной стороны, это было сделано, чтобы не усложнять модель и закон управления. С другой стороны, такую зависимость легко ввести, если вместо производных $M_x^{omega_x}$ и $M_x^{delta_a}$ использовать величины $M_x^{omega_x}/V^2$ и $M_x^{delta_a}/V^2$, определённые при заданной скорости полёта $V$.
  • Разработанный закон управления является программным управлением без обратной связи. Наличие обратной связи по угловой скорости и/или по углу крена позволит повысить точность выполнения фигуры, что и будет сделано в дальнейшем.

Выводы

В результате проведённой работы мы показали один из способов создания модели движения ДПЛА по угловой скорости $omega_x$. В лётном эксперименте было доказано, что созданная модель движения вполне соответствует моделируемому объекту. На основании разработанной модели получен закон программного управления, позволяющий выполнять «бочку» в автоматическом режиме. Также мы убедились, что выполнить правильную «бочку» одними элеронами не получится, а также наглядно это продемонстрировали.

Следующим этапом будет доработка закона управления путём добавления обратной связи, а также включение в управление руля высоты. Последнее потребует создание модели продольного движения нашего самолёта. По результатам работы выйдет следующая публикация.

Автор: RideaPlane

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js