Создаём собственный физический 2D-движок

Часть 2: ядро движка.

В этой части статьи мы добавим к разрешению импульсов силы другие функции. В частности, мы рассмотрим интегрирование, метки времени, использование в коде модульной архитектуры и распознавание коллизий в широкой фазе.

---

Введение

В предыдущем посте я рассмотрел тему разрешения импульсов силы. Прочитайте сначала его, если вы ещё это не сделали!

Давайте углубимся в темы, рассмотренные в этой статье. Все эти темы необходимы для любого более-менее достойного физического движка, поэтому настало время для создания новых функций поверх основы, заложенной в предыдущем посте.

• Интегрирование
• Метки времени
• Модульная архитектура
  • Тела
  • Формы
  • Силы
  • Материалы
• Широкая фаза
  • Отсечение дубликатов контактных пар
  • Система слоёв
• Проверка пересечения полупространств

---

Интегрирование

Интегрирование очень просто в реализации, и в Интернете есть много информации об итеративном интегрировании. В этом разделе я в основном рассмотрю функцию правильного интегрирования, и подскажу места, где можно найти более подробную информацию, если вам будет интересно.

Во-первых, нужно разобраться с тем, что же такое ускорение. Второй закон Ньютона гласит:

Он утверждает, что сумма всех сил, действующих на объект, равна массе этого объекта m, умноженной на ускорение a. m указывается в килограммах, a — в метрах/с, а F — в ньютонах.

Немного преобразуем уравнение для вычисления a и получим:

Следующий этап включает в себя ускорение для перемещения объекта из одного места в другое. Поскольку игра отображается в дискретных отдельных кадрах, создающих иллюзию анимации, необходимо вычислить места каждой из позиций этих дискретных шагов. Более подробный анализ этих уравнений см. в демо интегрирования Эрина Катто с GDC 2009 и в дополнении Ханну к симплектическому методу Эйлера для повышения стабильности в средах с низким FPS.

Интегрирование явным методом Эйлера показано в следующем фрагменте кода, где x — это позициия, а v — скорость. Стоит заметить, что, как объяснено выше, 1/m * F — это ускорение:

// Явный метод Эйлера
x += v * dt
v += (1/m * F) * dt

dt здесь обозначает дельту (прирост) времени. Δ — это символ дельты, и его можно буквально прочитать как «изменение в величине», или записать как Δt. Поэтому когда вы видите dt, это можно читать как «изменение времени». dv — это «изменение скорости».

Эта система будет работать и обычно она используется как отправная точка. Однако в ней есть численные неточности, от которых можно без лишних хлопот избавиться. Вот алгоритм, который называется симплектическим методом Эйлера:

// Симплектический метод Эйлера
v += (1/m * F) * dt
x += v * dt

Заметьте, что я всего лишь преобразовал порядок двух строк кода — см. вышеупомянутую статью Ханну.

В этом посте объясняются численные неточности явного метода Эйлера, но учтите, что Ханну начинает рассматривать RK4, который лично я не рекомендую: gafferongames.com: неточность метода Эйлера.

Этих простых уравнений достаточно для перемещения всех объектов с линейной скоростью и ускорением.

---

Метки времени

Поскольку игры отображаются с дискретными интервалами времени, нам требуется способ управляемой манипуляции временем между этими шагами. Видели ли вы когда-нибудь игру, которая работает на разных компьютерах с разной скоростью? Это пример игры, выполняемой со скоростью, зависящей от мощности компьютера.

Нам нужен способ, чтобы обеспечить выполнение физического движка только по прохождении определённого количества времени. Таким образом используемая в вычислениях dt всегда будет оставаться одним и тем же числом. Если везде в коде мы будем использовать точное постоянное значение dt, то наш физический движок превратится в детерминированный, а это его свойство известно как постоянная метка времени. Это очень удобная штука.

Детерминированный физический движок — это такой движок, который при одинаковом вводе всегда будет делать одно и то же. Это необходимо во многих типах игр, в которых геймплей должен быть чётко привязан к поведению физического движка. Кроме того, это необходимо для отладки нашего движка, потому что для выявления ошибок поведения движка оно должно быть неизменным.

Для начала давайте рассмотрим простую версию постоянной метки времени. Вот пример:

const float fps = 100
const float dt = 1 / fps
float accumulator = 0

// Единицы измерения - секунды
float frameStart = GetCurrentTime( )

// основной цикл
while(true)
  const float currentTime = GetCurrentTime( )

  // Сохраняется время, прошедшее с начала последнего кадра
  accumulator += currentTime - frameStart( )

  // Записывается начало этого кадра
  frameStart = currentTime

  while(accumulator > dt)
    UpdatePhysics( dt )
    accumulator -= dt

  RenderGame( )

Этот код ждёт и рендерит игру, пока не пройдёт достаточно времени для обновления физики. Прошедшее время записывается, а дискретные блоки времени размером с dt берутся из accumulator и обрабатываются физикой. Это гарантирует, что в любых условиях физике передаётся одинаковое значение, и что переданное физике значение является точным отображением действительного времени, прошедшего в реальной жизни. Блоки dt удаляются из accumulator, пока accumulator не становится меньше блока dt.

Здесь мы можем устранить пару проблем. Первая связана с тем, сколько времени требуется на обновление физики: что будет, если обновление физики займёт слишком много времени и с каждым игровым циклом accumulator будет всё больше и больше? Это называется «спиралью смерти». Если не решить эту проблему, то движок быстро придёт к полному останову, если расчёт физики будет недостаточно быстрым.

Для решения проблемы движку нужно меньше обновлений физики, если accumulator становится слишком большим. Один из простейших способов сделать это — ограничить accumulator, чтобы он не мог быть больше какого-нибудь произвольного значения.

const float fps = 100
const float dt = 1 / fps
float accumulator = 0

// Единицы измерения - секунды
float frameStart = GetCurrentTime( )

// основной цикл
while(true)
  const float currentTime = GetCurrentTime( )

  // Сохраняется время, прошедшее с начала последнего кадра
  accumulator += currentTime - frameStart( )

  // Записывается начало этого кадра
  frameStart = currentTime

  // Избавляемся от спирали смерти и ограничиваем dt, таким образом
  // ограничивая количество вызовов UpdatePhysics за
  // один игровой цикл.
  if(accumulator > 0.2f)
    accumulator = 0.2f

  while(accumulator > dt)
    UpdatePhysics( dt )
    accumulator -= dt

  RenderGame( )

Теперь, если выполняющая этот цикл игра обнаружит простой по каким-то причинам, то физика не утянет себя в спираль смерти. Игра просто будет выполняться немного медленнее, как и следует.

Следующая проблема гораздо меньше по сравнению со спиралью смерти. Этот цикл получает блоки dt из accumulator, пока accumulator не становится меньше dt. Это здорово, но в accumulator всё равно остаётся немного времени. В этом заключается проблема.

Допустим, что в accumulator каждый кадр остаётся 1/5 от блока dt. На шестом кадре в accumulator будет достаточно оставшегося времени на выполнение ещё одного обновления физики для всех других кадров. Это приведёт к тому, то примерно в одном кадре в секунду, или около того, будет выполняться немного больший дискретный прыжок во времени, и это может быть очень заметно в игре.

Чтобы решить эту проблему, необходимо использовать линейную интерполяцию. Звучит пугающе, но не бойтесь — я покажу реализацию. Если вы хотите понять, как её реализуют, то в Интернете есть множество ресурсов, посвящённых линейной интерполяции.

// линейная интерполяция для a от 0 до 1
// от t1 до t2
t1 * a + t2(1.0f - a)

С помощью этого кода мы сможем интерполировать (аппроксимировать) место, в котором мы можем находиться между двумя различными интервалами времени. Эту позицию можно использовать для рендеринга состояния игры между двумя обновлениями физики.

С помощью линейной интерполяции можно выполнять рендеринг движка со скоростью, отличающейся от выполнения физического движка. Это позволяет элегантно обрабатывать остаток accumulator от обновлений физики.

Вот полный пример:

const float fps = 100
const float dt = 1 / fps
float accumulator = 0

// Единицы измерения - секунды
float frameStart = GetCurrentTime( )

// основной цикл
while(true)
  const float currentTime = GetCurrentTime( )

  // Сохраняется время, прошедшее с начала последнего кадра
  accumulator += currentTime - frameStart( )

  // Записывается начало этого кадра
  frameStart = currentTime

  // Избавляемся от спирали смерти и ограничиваем dt, таким образом
  // ограничивая количество вызовов UpdatePhysics за
  // один игровой цикл.
  if(accumulator > 0.2f)
    accumulator = 0.2f

  while(accumulator > dt)
    UpdatePhysics( dt )
    accumulator -= dt

  const float alpha = accumulator / dt;

  RenderGame( alpha )

void RenderGame( float alpha )
  for shape in game do
    // вычисляем интерполированную трансформацию для рендеринга
    Transform i = shape.previous * alpha + shape.current * (1.0f - alpha)
    shape.previous = shape.current
    shape.Render( i )

Таким образом, все объекты в игре могут отрисовываться в переменные моменты между дискретными метками времени физики. Это позволяет элегантно обрабатывать все ошибки и накопление остатка времени. На самом деле рендеринг будет выполняться немного позже вычисленной физики, но при наблюдении за игрой всё движение замечательно сглаживается интерполяцией.

Игрок никогда не догадается, что рендеринг постоянно отстаёт от физики, потому что он будет знать только то, что видит, а видеть он будет идеально плавные переходы от одного кадра к другому.

Вы можете задаться вопросом: почему мы не интерполируем из текущей позиции до следующей? Я пробовал так сделать и оказалось, что для этого требуется, чтобы рендеринг «догадывался», где объекты будут находиться в будущем. Объекты в физическом движке часто могут внезапно менять своё движение, например, при коллизциях, и когда такие резкие изменения происходят, объекты телепортируются в другое место из-за неточных интерполяций на будущее.

---

Модульная архитектура

Каждому физическому объекту требуется несколько свойств. Однако параметры для каждого конкретного объекта могут слегка отличаться. Нам необходим умный способ для упорядочивания всех этих данных, и мы будем считать, что для такого упорядочивания желательно написать как можно меньше кода. В таком случае нам приходится модульная архитектура.

Словосочетание «модульная архитектура» может звучать пафосно и переусложнённо, но на самом деле оно вполне логично и довольно просто. В этом контексте под «модульной архитектурой» всего лишь подразумевается, что мы можем разбить физические объекты на отдельные части, чтобы можно было соединять и разъединять их удобным способом.

Тела

Физическое тело — это объект, содержащий всю информацию о каком-то конкретном физическом объекте. В нём будут храниться форма (или формы), из которых состоит объект, данные о массе, трансформации (позиция, поворот), скорость, крутящий момент, и т.д. Вот как будет выглядеть тело body:

struct body
{
  Shape *shape;
  Transform tx;
  Material material;
  MassData mass_data;
  Vec2 velocity;
  Vec2 force;
  real gravityScale;
};

Это отличная отправная точка для создания структуры физического тела. Здесь приняты логичные решения для создания хорошей структуры кода.

Во-первых, стоит заметить, что форма помещается в тело с помощью указателя. Благодаря этому создаётся слабая связь между телом и его формой. Тело может содержать любую форму, а форма тела может произвольно изменяться. На самом деле, тело может быть представлено несколькими формами, и такое тело будет называться «составным», потому что состоит из нескольких форм. (В этом туториале я не буду рассматривать составные тела.)

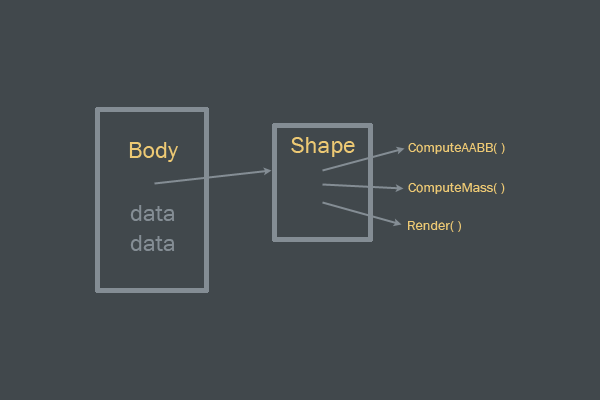
Интерфейс тела и формы.

Сам shape ответственен за вычисление граничных форм, вычисления массы на основании плотности и за рендеринг.

mass_data — это небольшая структура данных для хранения связанной с массой информации:

struct MassData
{
  float mass;
  float inv_mass;

  // Для вращений (будут рассматриваться ниже)
  float inertia;
  float inverse_inertia;
};

Очень удобно хранить в единой структуре все значения, связанные с массой и инерцией. Массу никогда не стоит задавать вручную — масса всегда должна вычисляться из самой формы. Масса — это довольно неинтуитивный тип значения, и задание её вручную потребует много времени на тонкую настройку. Она задаётся следующим образом:

Когда дизайнеру нужно, чтобы форма была более «массивной» или «тяжёлой», то ему стоит изменять плотность формы. Эту плотность можно использовать для вычисления массы формы с помощью её объёма. Это правильный способ действий в такой ситуации, потому что на плотность не влияет объём и она никогда не меняется во время выполнения игры (если только это не обеспечивается специальным кодом).

Некоторые из примеров форм, таких как AABB и окружности, можно найти в предыдущей части туториала.

Материалы

Все эти разговоры о массе и плотности приводят нас к вопросу: где же хранится значение плотности? Оно находится в структуре Material:

struct Material
{
  float density;
  float restitution;
};

После задания значений материала этот материал можно передать форме тела, чтобы тело могло вычислить массу.

Последнее, о чём стоит упомянуть — это gravity_scale. Масштабирование гравитации для разных объектов очень часто пригождается при тонкой настройке игрового процесса, поэтому в каждое тело стоит добавить это значение специально под эту задачу.

Полезные настройки для самых распространённых материалов можно использовать для создания значения перечисления объекта Material:

Rock       Density : 0.6  Restitution : 0.1
Wood       Density : 0.3  Restitution : 0.2
Metal      Density : 1.2  Restitution : 0.05
BouncyBall Density : 0.3  Restitution : 0.8
SuperBall  Density : 0.3  Restitution : 0.95
Pillow     Density : 0.1  Restitution : 0.2
Static     Density : 0.0  Restitution : 0.4

Силы

Надо обсудить ещё один аспект в структуре body. Это элемент данных под названием force. В начале каждого обновления физики это значение равно нулю. Другие воздействия физического движка (например, гравитация) добавляют к этому элементу данных force векторы Vec2. Непосредственно перед интегрированием все эти силы используются для вычисления ускорения тела и применяются на этапе интегрирования. После интегрирования этот элемент данных force обнуляется.

Это позволяет действовать на объект любому количеству сил, и для приложения к объектам новых видов сил не потребуется написание нового кода.

Давайте возьмём пример. Допустим, у нас есть небольшая окружность, представляющая собой очень тяжёлый объект. Эта маленькая окружность летает по миру игры, и она настолько тяжела, что постоянно немного притягивает к себе другие объекты. Вот грубый псевдокод для демонстрации этого:

HeavyObject object
for body in game do
  if(object.CloseEnoughTo( body )
    object.ApplyForcePullOn( body )

Функция ApplyForcePullOn() может относиться к небольшой силе, притягивающей body к HeavyObject, только если body находится достаточно близко.

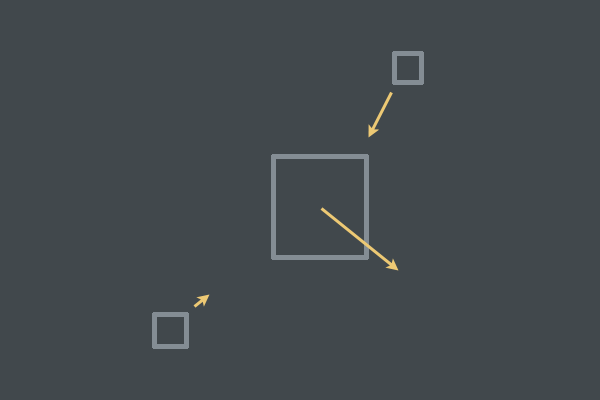
Два объекта, притянутые к большему объекту, двигающемуся мимо них. Силы притяжения зависят от расстояния до большого прямоугольника.

Не важно, сколько сил прикладывается к force тела, потому что они суммируются в единый общий вектор этого тела. Это значит, что две силы, действующие на одно тело, потенциально могут уравновесить друг друга.

---

Широкая фаза

В предыдущей статье серии мы ввели процедуры распознавания коллизий. Эти процедуры на самом деле независимы от того, что называется «узкой фазой». Различия между широкой и узкой фазами можно довольно просто найти в Google.

(Вкратце: мы используем широкую фазу распознавания коллизий для определения того, какие пары объектов могут сталкиваться, а затем узкую фазу распознавания коллизий, чтобы проверить, действительно ли они сталкиваются.)

Я хочу привести пример кода с объяснением того, как реализовать широкую фазу вычислений пар алгоритма с временной сложностью .

означает, что время, потраченное на проверку каждой пары потенциальных коллизий, зависит от квадрата количества объектов. Здесь используется нотация «О» большое.

Так как мы работаем с парами объектов, то будет полезно создать подобную структуру:

struct Pair
{
  body *A;
  body *B;
};

Широкая фаза должна собрать группу возможных коллизий и сохранить их все в структурах Pair. Затем эти пары могут быть переданы другой части движка (узкой фазе) для последующего решения.

Пример широкой фазы:

// Генерирует список пар.
// При вызове этой функции все предыдущие пары сбрасываются.
void BroadPhase::GeneratePairs( void )
{
  pairs.clear( )

  // Пространство кэша для AABB, которое будут использоваться
  // для вычисления граничного прямоугольника каждой формы
  AABB A_aabb
  AABB B_aabb

  for(i = bodies.begin( ); i != bodies.end( ); i = i->next)
  {
    for(j = bodies.begin( ); j != bodies.end( ); j = j->next)
    {
      Body *A = &i->GetData( )
      Body *B = &j->GetData( )

      // Пропуск проверки с самим собой
      if(A == B)
        continue

      A->ComputeAABB( &A_aabb )
      B->ComputeAABB( &B_aabb )

      if(AABBtoAABB( A_aabb, B_aabb ))
        pairs.push_back( A, B )
    }
  }
}

Приведённый выше код довольно прост: проверяем каждое тело с каждым другим телом, и пропускаем проверки коллизий с самим собой.

Отсечение дубликатов

В последнем разделе есть одна проблема: будет возвращаться множество дубликатов пар! Эти дубликаты нужно убрать из результатов. Если у вас нет под рукой библиотеки сортировки, то для этого понадобится знакомство с алгоритмами сортировки. Если вы пишете на C++, то вам повезло:

// Сортируем пары для выявления дубликатов
sort( pairs, pairs.end( ), SortPairs );

// Создаём очередь из многообразий для решения
{
  int i = 0;
  while(i < pairs.size( ))
  {
    Pair *pair = pairs.begin( ) + i;
    uniquePairs.push_front( pair );

    ++i;

    // Пропускаем дубликаты, выполняя итерации, пока не найдём уникальную пару
    while(i < pairs.size( ))
    {
      Pair *potential_dup = pairs + i;
      if(pair->A != potential_dup->B || pair->B != potential_dup->A)
        break;
      ++i;
    }
  }
}

После сортировки всех пар в определённом порядке можно считать, что у всех пар в контейнере pairs есть по соседству дубликат. Поместим все уникальные пары в новый контейнер uniquePairs, и на этом работа по отсечению дубликатов закончена.

The last thing to mention is the predicate SortPairs(). Эта функция SortPairs() используется для сортировки. Она может выглядеть вот так:

bool SortPairs( Pair lhs, Pair rhs )
{
  if(lhs.A < rhs.A)
    return true;

  if(lhs.A == rhs.A)
    return lhs.B < rhs.B;

  return false;
}

Члены lhs и rhs можно расшифровать как «left hand side» (сторона слева) и «right hand side» (сторона справа). Эти члены обычно используются для работы с параметрами функций, в которых элементы можно логически рассматривать как левую и правую часть какого-то уравнения или алгоритма.

Система слоёв

Система слоёв нужна для того, чтобы различные объекты никогда не сталкивались друг с другом. Она необходима, чтобы пули, летящие от определённых объектов, не влияли на другие определённые объекты. Например, игроки одной команды ракетами должны наносить урон врагам, но не друг другу.

Объяснение системы слоёв: некоторые объекты сталкиваются друг с другом, другие же нет.

Систему слоёв лучше всего реализовать с помощью битовых масок. Чтобы узнать, как битовые маски используются в движках, см. для ознакомления краткое введение в битовые маски для программистов, страницу на Википедии и раздел Filtering в руководстве Box2D.

Система слоёв реализуется в широкой фазе. Здесь я просто вставлю готовый пример широкой фазы:

// Генерирует список пар.
// При вызове этой функции все предыдущие пары сбрасываются.
void BroadPhase::GeneratePairs( void )
{
  pairs.clear( )

  // Пространство кэша для AABB, которое будут использоваться
  // для вычисления граничного прямоугольника каждой формы
  AABB A_aabb
  AABB B_aabb

  for(i = bodies.begin( ); i != bodies.end( ); i = i->next)
  {
    for(j = bodies.begin( ); j != bodies.end( ); j = j->next)
    {
      Body *A = &i->GetData( )
      Body *B = &j->GetData( )

      // Пропуск проверки с самим собой
      if(A == B)
        continue

      // Учитываться тольк соответствующие слои
      if(!(A->layers & B->layers))
        continue;

      A->ComputeAABB( &A_aabb )
      B->ComputeAABB( &B_aabb )

      if(AABBtoAABB( A_aabb, B_aabb ))
        pairs.push_back( A, B )
    }
  }
}

Система слоёв оказывается высокоэффективной и очень простой.

---

Пересечение полупространств

Полупространство можно рассматривать в 2D как одну сторону прямой. Определение того, находится ли точка на одной или другой стороне прямой — довольно распространённая задача, и при реализации собственного физического движка нужно хорошо разобраться в ней. Очень плохо, что эта тема, как мне кажется, нигде в Интернете подробно не раскрыта, и мы это исправим!

Общее уравнение прямой в 2D имеет следующий вид:

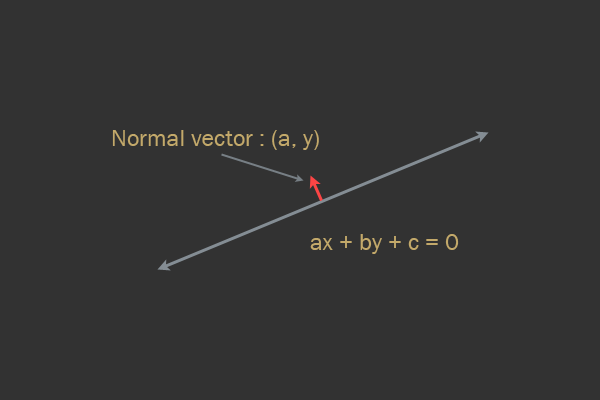
Учтите, что несмотря на своё название, вектор нормали не всегда обязательно нормализирован (то есть он не обязательно имеет длину 1).

Чтобы определить, находится ли точка на определённой стороне прямой, всё, что нам нужно — подставить точку в переменные x и y уравнения и проверить знак результата. Результат 0 будет означать, что точка находится на прямой, а положительное/отрицательное значение означают разные стороны прямой.

И на этом всё! Зная это, от точки до прямой является результатом предыдущей проверки. Если вектор нормали не нормализован, то результат отмасштабирован на величину вектора нормали.

---

Заключение

К этому этапу вы можете создать с нуля полный, хотя и очень простой физический движок. В следующих частях мы рассмотрим более сложные темы: трение: ориентация, и динамическое дерево AABB.

Часть 3: трение, сцена и таблица переходов

В этой части статьи мы рассмотрим следующие темы:

• Трение
• Сцена
• Таблица переходов коллизий

---

Видео демо

Вот краткое демо того, над чем мы будем работать в этой части:

---

Трение

Трение — это часть системы разрешения коллизий. Трение всегда прикладывается к силе, приложенной к объектам, в направлении, противоположном их движению.

В реальной жизни трение — это невероятно сложное взаимодействие между различными веществами и для его моделирования принимаются серьёзные допущения и аппроксимации. Эти допущения относятся к математике и обычно формулируются примерно так: «трение можно приближенно представить как один вектор», аналогично тому, как динамика твёрдых тел симулирует взаимодействия реального мира, допуская использование недеформируемых тел с одинаковой по всему объёму плотностью.

Взгляните на видео демо из первой части статьи:

Взаимодействия между телами достаточно интересны, а отталкивание при коллизиях выглядит реалистично. Однако когда объекты приземляются на неподвижную платформу, то все они как будто отталкиваются и скользят с краёв экрана. Так получается из-за отсутствия симуляции трения.

Импульсы силы, снова?

Как вы наверно помните из первой части туториала, для разделения проникновения двух объектов при коллизии необходимо значение j, представляющее собой величину импульса силы. Эту величину можно обозначить как jnormal или jN, потому что она используется для изменения скорости вдоль нормали коллизии.

Для добавления реакции трения необходимо вычислить ещё одну величину, обозначаемую как jtangent или jT. Трение можно смоделировать как импульс силы. Эта величина будет изменять скорость объекта вдоль отрицательного касательного вектора коллизии, или, другими словами, вдоль вектора трения. В двух измерениях вычисление вектора трения является решаемой задачей, но в 3D она становится гораздо сложнее.

Трение довольно просто, и мы можем снова воспользоваться нашим предыдущим уравнением для j, только заменим все нормали n на касательный вектор t.

Заменим n на t:

Хотя в этом уравнении на t заменено всего одно вхождение n, после добавления вращения необходимо будет заменить ещё несколько вхождений, кроме одного в числителе Уравнения 2.

Теперь возникает вопрос, как же вычислить t. Касательный вектор — это вектор, перпендикулярный нормали коллизии, который направлен ближе к нормали. Это может сбивать с толку — не волнуйтесь, у нас есть рисунок!

На рисунке ниже видно, что касательный вектор перпендикулярен нормали. Касательный вектор может быть направлен влево или вправо. Если влево, то он «дальше» от относительной скорости. Однако он определяется как перпендикуляр к нормали, направленный «ближе» к относительной скорости.

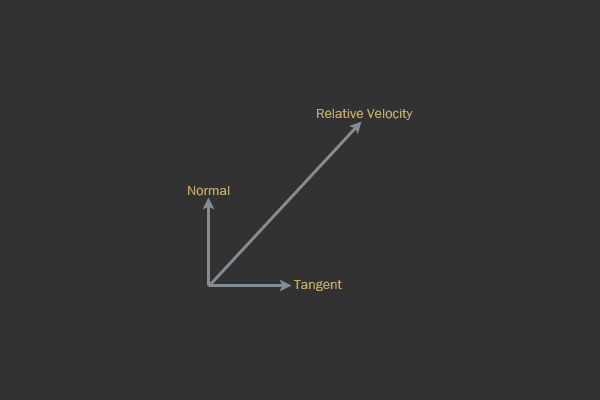
Различные виды векторов в кадре времени коллизии твёрдых тел.

Как было вкратце рассказано выше, трение будет вектором, направленным в противоположную от касательного вектора сторону. Это значит, что направление, в котором мы прикладываем трение, можно вычислить непосредственно, потому что вектор нормали находится при распознавании коллизий.

Если мы знаем это, то касательный вектор равен (где n — нормаль коллизии):

Чтобы определить величину трения jt, нам осталось только непосредственно вычислить значение из представленных выше уравнений. Вскоре мы рассмотрим и другие хитрости после вычисления этого значения, поэтому это не единственное, что нужно для нашего разрешения коллизий:

// Перерасчёт относительной скорости после приложения
// нормального импульса (импульса силы из первой статьи, этот код идёт сразу
// после в той же функции разрешения)
Vec2 rv = VB - VA

// Вычисляем касательный вектор
Vec2 tangent = rv - Dot( rv, normal ) * normal
tangent.Normalize( )

// Вычисляем величину, прилагаемую вдоль вектора трения
float jt = -Dot( rv, t )
jt = jt / (1 / MassA + 1 / MassB)

Вышеприведённый код непосредственно соответствует Уравнению 2. Повторюсь, важно понимать, что вектор трения указывает в направлении, противоположном касательному вектору. Поэтому мы должны добавить знак «минус» при скалярном произведении относительной скорости по касательной, чтобы вычислить относительную скорость вдоль касательного вектора. Знак «минус» переворачивает касательную скорость и внезапно указывает в направлении, в котором должно аппроксимироваться трение.

Закон Амонтона — Кулона

Закон Амонтона — Кулона — это та часть симуляции трения, в которой испытывают затруднение большинство программистов. Мне самому пришлось достаточно долго изучать его, чтобы найти правильный способ моделирования. Хитрость в том, что закон Амонтона — Кулона — это неравенство.

Он гласит:

Другими словами, сила трения всегда меньше или равна нормальной силе, умноженной на некую константу μ (значение которой зависит от материалов объектов).

Нормальная сила — это просто наша старая величина j, умноженная на нормаль коллизии. Так что если вычисленная jt (представляющая собой силу трения) меньше нормальной силы в μ раз, то мы можем использовать нашу величину jt в качестве трения. Если же нет, то вместо неё надо использовать нормальную силу, умноженную на μ. Это условие «если» ограничивает наше трение каким-то максимальным значением, где максимумом будет нормальная сила, умноженная на μ.

Весь смысл закона Амонтона — Кулона в том, чтобы выполнить эту процедуру ограничения. Такое ограничение оказывается самой сложной частью симуляции трения для разрешения на основании импульсов силы — по ней нигде не найти документации, но сейчас мы это исправим! В большинстве найденных мною статей по этой теме трение или совершенно отбрасывается, или упоминается вкратце, а процедуры ограничения реализуются неправильно (или вообще не существуют). Надеюсь, теперь вы осознаете, что правильное понимание этой части очень важно.

Прежде чем что-то объяснять, давайте полностью реализуем ограничение. Представленный ниже блок кода — это предыдущий пример с готовой процедурой ограничения и приложением импульса силы трения:

// Перерасчёт относительной скорости после приложения
// нормального импульса (импульса силы из первой статьи, этот код идёт сразу
// после в той же функции разрешения)
Vec2 rv = VB - VA

// Вычисляем касательный вектор
Vec2 tangent = rv - Dot( rv, normal ) * normal
tangent.Normalize( )

// Вычисляем величину, прилагаемую вдоль вектора трения
float jt = -Dot( rv, t )
jt = jt / (1 / MassA + 1 / MassB)

// PythagoreanSolve = A^2 + B^2 = C^2, вычисляем C для заданных A и B
// Используем для аппроксимации мю для заданных коэффициентов трения каждого тела
float mu = PythagoreanSolve( A->staticFriction, B->staticFriction )

// Ограничиваем величину трения и создаём вектор импульса силы
Vec2 frictionImpulse
if(abs( jt ) < j * mu)
  frictionImpulse = jt * t
else
{
  dynamicFriction = PythagoreanSolve( A->dynamicFriction, B->dynamicFriction )
  frictionImpulse = -j * t * dynamicFriction
}

// Прикладываем
A->velocity -= (1 / A->mass) * frictionImpulse
B->velocity += (1 / B->mass) * frictionImpulse

Я решил использовать эту формулу для определения коэффициентов трения между двумя телами при заданных для каждого тела коэффициентах:

На самом деле я уже видел, как кто-то использовал его в собственном физическом движке, и мне понравились результаты. Если нужно избавиться от квадратного корня, то отлично подойдёт среднее двух значений. На самом деле сработает любая форма подбора коэффициента трения, просто я предпочитаю эту. Ещё один вариант: можно использовать таблицу поиска, в которой тип каждого тела является индексом двухмерной таблицы.

Важно то, что в сравнении используется абсолютное значение jt, потому что теоретически сравнение ограничивает «сырые» величины каким-то порогом. Поскольку j всегда положительно, его нужно перевернуть, чтобы оно представляло истинный вектор трения в случае использования динамического трения.

Статическое и динамическое трение

В предыдущем фрагменте кода без каких-либо объяснений были введены статическое и динамическое трение. Я посвящу целый раздел объяснению разницы между ними и необходимости этих двух типов значений.

При трении происходит кое-что интересное: чтобы объекты перешли из состояния покоя в движение, им требуется «энергия активации». Когда два объекта покоятся один на другом в реальной жизни, требуется довольно большая энергия, чтобы столкнуть один из них и заставить двигаться. Однако когда мы заставили объект скользить по другому, часто после этого для поддержания скольжения требуется меньше энергии.

Так происходит из-за принципа работы трения на микроскопическом уровне. Здесь поможет ещё одна иллюстрация:

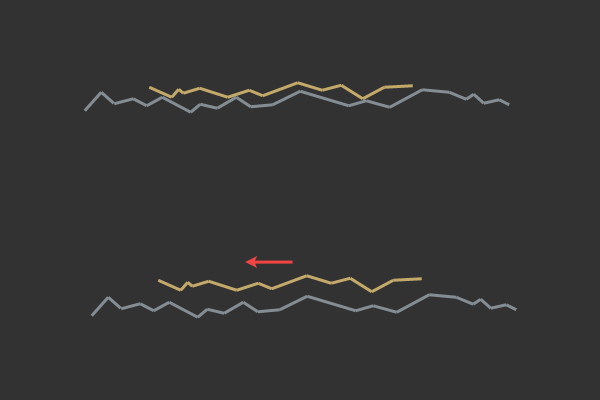
Микроскопические причины необходимости энергии активации при трении.

Как вы видите, на самом деле основным препятствием, создающим трение, являются небольшие неровности между поверхностями. Когда один объект покоится поверх другого, микроскопические неровности находятся в покое между объектами, связывая их. Эту связь нужно разорвать или разделить, чтобы объекты могли скользить друг относительно друга.

Нам необходимо найти способ смоделировать это внутри движка. Простейшее решение будет таким: дать каждому типу материала два значения трения — одно для статического, второе для динамического.

Статическое трение используется для ограничения величины jt. Если при вычислении величины jt она оказывается слишком малой (ниже нашего порога), то мы можем считать, что объект находится в покое, или близко к нему, и используем всю величину jt в качестве импульса силы.

С другой стороны, если при вычислении jt величина выше порога, то можно считать, что объект уже превысил «энергию активации», и в такой ситуации используется меньший импульс силы трения, что выражается в меньшем коэффициенте трения и немного ином вычислении импульса силы.

---

Сцена

Если вы внимательно прочитали раздел «Трение», то поздравляю! Вы завершили самую сложную (по моему мнению) часть всего туториала.

Класс Scene используется в качестве контейнера для всего, относящегося к сценарию физической симуляции. Он вызывает и использует результаты всех широких фаз, содержит все твёрдые тела, выполняет проверки коллизий и вызывает их разрешение. Также он сочетает в себе все активные объекты. Также сцена взаимодействует с пользователем (например, программистом, использующим физический движок).

Вот пример того, как может выглядеть структура сцены:

class Scene
{
public:
  Scene( Vec2 gravity, real dt );
  ~Scene( );

  void SetGravity( Vec2 gravity )
  void SetDT( real dt )

  Body *CreateBody( ShapeInterface *shape, BodyDef def )

  // Вставляет тело в сцену и инициализирует тело (вычисляет массу).
  void InsertBody( Body *body )

  // Удаляет тело из сцены
  void RemoveBody( Body *body )

  // Обновляет сцену одной меткой времени
  void Step( void )

  float GetDT( void )
  LinkedList *GetBodyList( void )
  Vec2 GetGravity( void )
  void QueryAABB( CallBackQuery cb, const AABB& aabb )
  void QueryPoint( CallBackQuery cb, const Point2& point )

private:
  float dt     // Метка времени в секундах
  float inv_dt // Величина, обратная метке времени в секундах
  LinkedList body_list
  uint32 body_count
  Vec2 gravity
  bool debug_draw
  BroadPhase broadphase
};

В классе Scene нет ничего особо сложного. Идея заключается в том, чтобы позволить пользователю удобно добавлять и удалять твёрдые тела. BodyDef — это структура, содержащая всю информацию о твёрдом теле, она может использоваться для вставки пользователем значений в чём-то вроде структуры конфиругации.

Ещё одной важной функцией является Step(). Эта функция выполняет один этап проверки коллизий, разрешения и интегрирования. Её нужно вызывать из цикла меток времени, созданного во второй части туториала.

При запросах точки или AABB выполняется проверка того, какие из объектов действтиельно сталкиваются в сцене точкой или AABB. Благодаря этому связанной с геймплеем логике проще понять, как объекты расположены в мире.

---

Таблица переходов

Нам нужен простой способ выбора вызываемой функции коллизий в зависимости от типа двух разных объектов.

В C++ мне известны два основных способа: двойная диспатчеризация (double dispatch) и двухмерная таблица переходов. В своих тестах я выяснил, что двухмерная таблица оптимальней, поэтому я буду подробно рассматривать её реализацию. Если вы планируете использовать не C и не C++, то я уверен, что аналогично таблице указателей функций можно создать массив функций или функциональных объектов (и это ещё одна причина выбора таблиц перехода, а не других вариантов, которые специфичны для C++).

Таблица переходов в C или C++ — это таблица указателей функций. Индексы, представляющие собой произвольные имена или константы, используются как индекс таблицы и для вызова конкретной функции. Использование одномерной таблицы переходов может выглядеть следующим образом:

enum Animal
{
  Rabbit
  Duck
  Lion
};

const void (*talk)( void )[] = {
  RabbitTalk,
  DuckTalk,
  LionTalk,
};

// Вызываем функцию из таблицы с одномерной виртуальной диспатчеризацией
talk[Rabbit]( ) // Вызываем функцию RabbitTalk

Вышеприведённый код на самом деле имитирует то, что сам язык C++ реализует через вызов виртуальных функций и наследование. Однако в C++ реализуются только одномерные вызовы виртуальных функций. Двухмерную таблицу можно построить вручную.

Вот псевдокод для двухмерной таблицы переходов для вызова процедур коллизий:

collisionCallbackArray = {
  AABBvsAABB
  AABBvsCircle
  CirclevsAABB
  CirclevsCircle
}

// Вызываем процедуру коллизий для распознавания коллизии между
// двумя коллайдерами A and B, не зная их точного типа коллайдера
// тип может быть AABB или окружностью
collisionCallbackArray[A->type][B->type]( A, B )

И на этом всё! Истинные типы каждого из коллайдеров можно использовать в качестве индексов двухмерного массива и выбора функции для разрешения коллизии.

Однако стоит заметить, что AABBvsCircle и CirclevsAABB являются дубликатами. Необходимы обе функции! Для одной из этих функций необходимо отразить нормаль, и в этом заключается их единственная разница. Это позволяет выполнять правильное разрешение коллизий вне зависимости от сочетания объектов.

---

Заключение

Мы уже рассмотрели множество тем, посвящённых созданию с нуля собственного физического движка для твёрдых тел! Пока мы изучили разрешение коллизий, трение и архитектуру движка. Имея эти знания, уже можно создать успешный физический движок для множества качественных двухмерных игр.

В следующей части мы рассмотрим ещё одну важную для движка тему: вращение и ориентация. Наблюдать за взаимодействием ориентированных объектов невероятно интересно, и они являются последней частью, которая необходима нашему физическому движку.

Разрешение вращения оказывается достаточно простым, однако распознавание коллизий становится сложнее.

Часть 4: ориентированные твёрдые тела

Итак, мы рассмотрели разрешение импульсов силы, архитектуру ядра и трение. В этой последней части туториала я раскрою очень интересную тему: ориентацию.

В этой части мы поговорим о следующих темах:

• Математика вращения
• Ориентированные формы
• Распознавание коллизий
• Разрешение коллизий

---

Пример кода

Я создал небольшой пример движка на C++ и рекомендую изучать исходный код в процессе чтения статьи, потому что многие подробности реализации не уместились в саму статью.

В этом репозитории GitHub содержится сам пример движка вместе с проектом Visual Studio 2010. Для удобства GitHub позволяет просматривать код без необходимости скачивания.

Другие статьи по теме

• Филип Диффендерфер форкнул репозиторий, чтобы создать Java-версию движка!

---

Математика ориентаций

Математика, относящаяся к вращениям в 2D, достаточно проста, однако для создания всего ценного в физическом движке требуется знание предмета. Второй закон Ньютона гласит:

Есть похожее уравнение, относящееся конкретно к вращающей силе и угловому ускорению. Однако прежде чем знакомиться с этими уравнениями, стоит вкратце описать векторное произведение в двухмерном пространстве.

Векторное произведение

Векторное произведение в 3D — это хорошо известная операция. Однако векторное произведение в 2D может довольно сильно сбивать с толку, потому что оно на самом деле не имеет удобной геометрической интерпретации.

Векторное произведение в 2D, в отличие от версии в 3D, возвращает не вектор, а скаляр. Это скалярное произведение на самом деле определяет величину ортогонального вектора вдоль оси Z, как будто векторное произведение выполняется в 3D. В каком-то смысле, векторное произведение в 2D — это упрощённая версия векторного произведения в 3D, потому что является расширением трёхмерной векторной математики.

Если вас это запутывает, не волнуйтесь: глубинное понимание векторных произведений в двухмерном пространстве нам не требуется. Достаточно просто точно знать, как выполнять эту операцию, и знать, что важен порядок операций: — это не одно и то же, что . В этой части мы будем активно использовать векторное произведение для преобразования угловой скорости в линейную.

Однако знание того, как выполняется векторное произведение в 2D тоже очень важно. Можно выполнить векторное произведение двух векторов, скаляра и вектора, или вектора и скаляра. Операции имеют следующий вид:

// Векторное произведение двух векторов возвращает скаляр
float CrossProduct( const Vec2& a, const Vec2& b )
{
  return a.x * b.y - a.y * b.x;
}

// Более экзотичные (но необходимые) виды векторных произведений
// с вектором a и скаляром s, оба возвращают вектор
Vec2 CrossProduct( const Vec2& a, float s )
{
  return Vec2( s * a.y, -s * a.x );
}

Vec2 CrossProduct( float s, const Vec2& a )
{
  return Vec2( -s * a.y, s * a.x );
}

Крутящий момент и угловая скорость

Как мы знаем из предыдущих частей, это уравнение обозначает связь между силой, действующей на тело, с массой и ускорением этого тела. У него есть аналог для вращения:

обозначает крутящий момент. Крутящий момент — это сила вращения.

— это вектор из центра масс (ЦМ) в определённую точку объекта. можно считать «радиусом» от ЦМ до точки. Для каждой уникальной точки объекта нужно своё значение для подстановки в Уравнение 2.

называется «омега» и обозначает скорость вращения. Это отношение будет использоваться для интегрирования угловой скорости твёрдого тела.

Важно понимать, что линейная скорость — это скорость ЦМ твёрдого тела. В предыдущей части у всех объектов не было компонентов вращения, поэтому линейная скорость ЦМ была такой же, что и скорость всех точек тела. При добавлении ориентации точки, удалённые от ЦМ, вращаются быстрее, чем ближние к ЦМ. Это значит, что нам нужно новое уравнение для нахождения скорости точки тела, потому что тела теперь одновременно могут вращаться и перемещаться.

Воспользуется следующим уравнением для понимания связи между точкой тела и скоростью этой точки:

обозначает линейную скорость. Для преобразования линейной скорости в угловую, необходимо найти векторное произведение радиуса и .

То есть мы можем преобразовать Уравнение 3 в другой вид:

Уравнения из предыдущего раздела справедливы, только если твёрдые тела имеют равномерную плотность. Неравномерная плотность делает всю математику, относящуюся к вращению и поведению твёрдого тела, слишком сложной. Более того, если тело, представляющее твёрдое тело, не находится в ЦМ, то вычисления с участием будут совершенно шаткими.

Инерция

В двух измерениях объект вращается вокруг воображаемой оси Z. Это вращение может быть достаточно сложным и зависит от того, насколько далеко от ЦМ находится масса объекта. Окружность с массой, равной массе длинного тонкого прутка, проще вращать, чем пруток. Этот фактор «сложности вращения» можно воспринимать как момент инерции объекта.

В каком-то смысле, инерция — это вращательная масса объекта. Чем большей инерцией он обладает, тем сложнее привести его во вращение.

Зная это, можно хранить инерцию объекта в структуре тела в том же формате, что и массу. Будет также логично хранить и величину, обратную значению инерции, и при этом быть аккуратными с делением на ноль. См. в предыдущих частях более подробную информацию о массе и обратной массе.

Интегрирование

Каждому твёрдому телу потребуется ещё несколько полей для хранения информации о вращении. Вот быстрый пример структуры, хранящей дополнительные данные:

struct RigidBody
{
  Shape *shape

  // Линейные компоненты
  Vec2 position
  Vec2 velocity
  float acceleration

  // Угловые компоненты
  float orientation // радианы
  float angularVelocity
  float torque
};

Интегрирование угловой скорости и ориентации тела очень похоже на интегрирование скорости и ускорения. Вот краткий пример кода демонстрирующий его выполнение (подробности интегрирования рассмотрены в предыдущей части):

const Vec2 gravity( 0, -10.0f )
velocity += force * (1.0f / mass + gravity) * dt
angularVelocity += torque * (1.0f / momentOfInertia) * dt
position += velocity * dt
orient += angularVelocity * dt

Имея тот малый объём информации, который мы изучили ранее, вы сможете без проблем начать вращать разные объекты на экране. Всего за несколько строк кода можно построить нечто более впечатляющее, например, забросив фигуру в воздух, пока она вращается вокруг ЦМ, а гравитация притягивает её вниз, создавая движение по дуге.

Mat22

Как показано выше, ориентацию нужно хранить как одно значение в радианах, однако часто для некоторых фигур удобнее хранить небольшую матрицу поворота.

Хорошим примером этого является ориентированный граничный прямоугольник (Oriented Bounding Box, OBB). OBB состоит из ширины и высоты, которые можно представить как векторы. Эти два вектора размерностей можно вращать с помощью матрицы поворота два на два, представляющей оси OBB.

Я рекомендую добавить в используемую вами математическую библиотеку класс матрицы Mat22. Сам я использую собственную небольшую математическую библиотеку, которая есть в демо открытых исходников. Вот пример того, как может выглядеть такой объект:

struct Mat22
{
  union
  {
    struct
    {
      float m00, m01
      float m10, m11;
    };

    struct
    {
      Vec2 xCol;
      Vec2 yCol;
    };
  };
};

Он имеет следующие полезные операции: создание по углу, создание по векторам столбцов, транспонирование, умножение на Vec2, умножение на другую Mat22, вычисление абсолютного значения.

Последняя функция позволит нам получить из вектора столбец x или y. Функция столбца работает примерно так:

Mat22 m( PI / 2.0f );
Vec2 r = m.ColX( ); // получаем столбец оси x

Эта техника полезна для получения единичного вектора вдоль оси вращения: x или y. Кроме того, матрицу два на два можно создать из двух ортогональных единичных векторов, потому что каждый вектор можно непосредственно вставить в строки. Хотя такой способ создания довольно необычен для двухмерных физических движков, он всё равно может быть полезен для общего понимания работы поворотов и матриц.

Этот конструктор может выглядеть примерно так:

Mat22::Mat22( const Vec2& x, const Vec2& y )
{
  m00 = x.x;
  m01 = x.y;
  m01 = y.x;
  m11 = y.y;
}

// или

Mat22::Mat22( const Vec2& x, const Vec2& y )
{
  xCol = x;
  yCol = y;
}

Поскольку самая важная операция матрицы поворота — это выполнение поворотов на основе угла, то важно иметь возможно создать матрицу из угла и умножить вектор на эту матрицу (чтобы повернуть вектор против часовой стрелки на угол, с которым была создана матрица):

Mat2( real radians )
{
  real c = std::cos( radians );
  real s = std::sin( radians );

  m00 = c; m01 = -s;
  m10 = s; m11 =  c;
}

// Вращаем вектор
const Vec2 operator*( const Vec2& rhs ) const
{
  return Vec2( m00 * rhs.x + m01 * rhs.y, m10 * rhs.x + m11 * rhs.y );
}

Ради краткости я не буду выводить, почему матрица поворота против часовой стрелки имеет следующий вид:

a = angle
cos( a ), -sin( a )
sin( a ),  cos( a )

Однако важно по крайней мере знать, что таков вид матрицы поворота. Подробнее о матрицах поворота можно прочитать на странице в Википедии.

Другие статьи по теме

• Создаём собственный программный 3D-движок, часть 2: линейные преобразования

---

Преобразование к базису

Важно понимать разницу между пространством модели и мира. Пространство модели — это система координат, локальная к физической форме. Её точка начала координат находится в ЦМ, а ориентация системы координат сонаправлена с осями самой фигуры.

Чтобы преобразовать фигуру в пространство мира, её нужно повернуть и переместить. Поворот выполняется в первую очередь, потому что он всегда выполняется относительно точки начала координат. Поскольку объект находится в пространстве модели (точка начала в ЦМ), поворот выполняется относительно ЦМ фигуры. Поворот выполняется с матрицей Mat22. В коде примера матрицы ориентации называются u.

После выполнения поворота объект можно переместить к его позиции в мире сложением векторов.

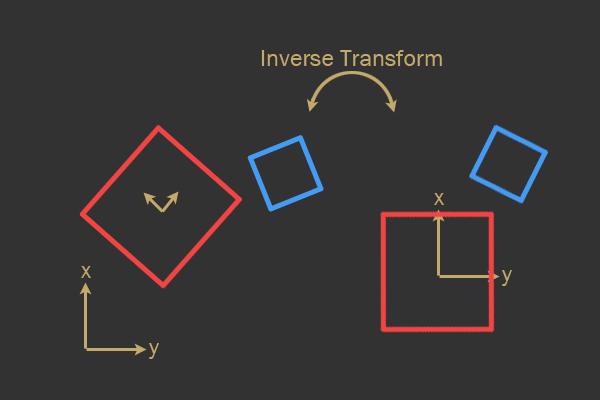
Когда объект находится в пространстве мира, его можно переместить в пространство модели совершенно другого объекта с помощью обратных преобразований. Для этого выполняются обратный поворот и обратное перемещение. Именно все эти математические вычисления упрощаются при распознавании коллизий!

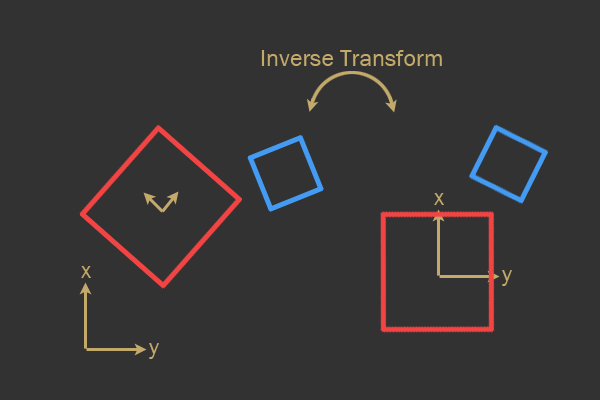
Обратное преобразование (слева направо) из пространства мира в пространство модели красного полигона.

Как видно из предыдущего изображения, обратное преобразование красного объекта применяется и к красному, и к синему полигону, то есть проверку распознавания коллизий можно ограничить видом проверки AABB и OBB, а не задействовать сложные математические вычисления между двумя ориентированными фигурами.

В большей части исходного кода примера вершины по разным причинам постоянно трансформируются из пространства модели в пространство мира, и обратно к модели. Вы должны иметь чёткое понимание того, что это значит, чтобы разобраться в примере кода распознавания коллизий.

---

Распознавание коллизий и генерирование многообразий

В этом разделе я представлю краткие обзоры коллизий полигонов и окружностей. Более глубокие подробности реализации см. в примере исходного кода.

Полигон с полигоном

Давайте начнём с самой сложной процедуры распознавания коллизий во всём этом туториале. Идея проверки коллизий между двумя полигонами наиболее удачно (по моему мнению) реализуется с помощью теоремы о разделяющей оси (Separating Axis Theorem, SAT).

Однако вместо проецирования размерностей каждого полигона друг на друга существует более новый и эффективный метод, описанный Дирком Грегориусом в лекции на GDC 2013 (бесплатные слайды лежат здесь).

Первое, что нужно понять — это концепция опорных точек.

Опорные точки

Опорная точка полигона — это вершина, наиболее удалённая в заданном направлении. Если две точки имеют одинаковое в заданном направлении расстояние, то выбрать можно любую из них.

Для вычисления опорной точки необходимо использовать скалярное произведение для нахождения расстояния со знаком вдоль заданного направления. Это очень просто, поэтому я покажу в статье краткий пример:

// Крайняя точка вдоль направления в полигоне
Vec2 GetSupport( const Vec2& dir )
{
  real bestProjection = -FLT_MAX;
  Vec2 bestVertex;

  for(uint32 i = 0; i < m_vertexCount; ++i)
  {
    Vec2 v = m_vertices[i];
    real projection = Dot( v, dir );

    if(projection > bestProjection)
    {
      bestVertex = v;
      bestProjection = projection;
    }
  }

  return bestVertex;
}

Скалярное произведение используется для каждой вершины. Скалярное произведение представляет собой расстояние со знаком в заданном направлении, то есть возвращаемой вершиной будет вершина с наибольшим спроецированным расстоянием. В примере движка эта операция выполняется в пространстве модели заданного полигона.

Поиск оси разделения

Благодаря концепции опорных точек можно выполнить поиск оси разделения между двумя полигонами (полигоном A и полигоном B). Идея этого поиска заключается в том, чтобы пройти в цикле по всем рёбрам полигона A и найти опорные точки в отрицательной нормали к ребру.

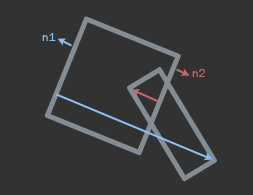
На приведённом выше изображении показаны две опорные точки, по одной для каждого объекта. Синяя нормаль будет соответствовать опорной точке на другом полигоне как самая дальняя вершина вдоль противоположного направления синей нормали. Аналогично, красная нормаль используется для нахождения опорной точки, расположенной в конце красной стрелки.

Расстояние от каждой опорной точки до текущего ребра будет глубиной проникновения со знаком. Сохранив наибольшее расстояние, можно записать ось наименьшего проникновения.

Вот пример функции из исходного кода, которая ищет возможную ось наименьшего проникновения с помощью функции GetSupport:

real FindAxisLeastPenetration( uint32 *faceIndex, PolygonShape *A, PolygonShape *B )
{
  real bestDistance = -FLT_MAX;
  uint32 bestIndex;

  for(uint32 i = 0; i < A->m_vertexCount; ++i)
  {
    // Получаем нормаль к ребру от A
    Vec2 n = A->m_normals[i];

    // Получаем опорную точку от B вдоль -n
    Vec2 s = B->GetSupport( -n );

    // Получаем вершину на ребре от A, преобразуем в
    // пространство модели B
    Vec2 v = A->m_vertices[i];

    // Вычисляем расстояние глубины проникновения (в пространстве модели B)
    real d = Dot( n, s - v );

    // Сохраняем наибольшее расстояние
    if(d > bestDistance)
    {
      bestDistance = d;
      bestIndex = i;
    }
  }

  *faceIndex = bestIndex;
  return bestDistance;
}

Поскольку эта функция возвращает наибольшую глубину проникновения, если эта глубина положительна, то это значит, что две фигуры не пересекаются (отрицательное проникновение означает, что разделяющей оси нет).

Эту функцию нужно вызывать дважды, меняя местами при каждом вызове объекты A и B.

Отсечение ребра соударения и базового ребра

На этом этапе стоит определить ребро соударения и базовое ребро, а ребро соударения необходимо отсечь относительно боковых плоскостей базового ребра. Это достаточно нетривиальная операция, хотя Эрин Катто (создатель Box2D и всей физики, используемой Blizzard) подготовил отличные слайды, подробно рассматривающие эту тему.

Это отсечение создаёт две возможные точки контакта. Все точки контакта за базовым ребром можно считать точками контакта.

Кроме того, что изложено на слайдах Эрина Катто, пример движка также содержит в качестве примера процедуры отсечения.

Окружность с полигоном

Процедура коллизии окружности и полигона намного проще, чем распознавание коллизии между полигоном и полигоном. Сначала с помощью способа, похожего на использование опорных точек из предыдущего раздела, вычисляется ближайшее к центру окружности ребро полигона: в цикле обходятся нормали каждого ребра полигона и находится расстояния от центра окружности до ребра.

Если центр окружности находится за этим ближайшим ребром, то можно сгенерировать информацию о контакте, после чего процедура сразу же завершается.

После нахождения ближайшего ребра проверка превращается в тест отрезка прямой и окружности. У отрезка прямой есть три интересных области, называемых областями Вороного. Посмотрите на схему:

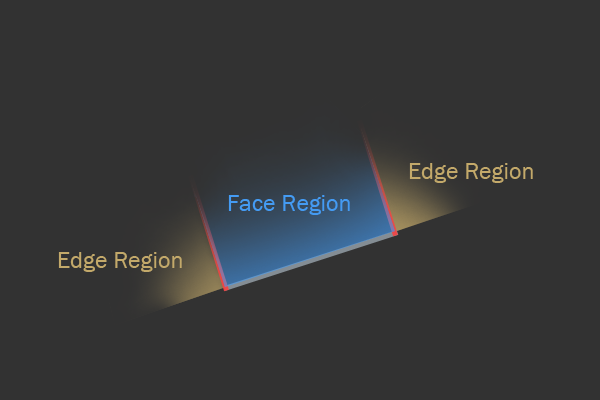
Области Вороного для отрезка прямой.

Интуитивно понятно, что в зависимости от того, где находится центр окружности, можно получить разную информацию о контакте. Представим, что центр окружности расположен в одной из областей вершины. Это значит, что ближайшая к центру окружности точка будет являться вершиной ребра, а правильной нормалью коллизии будет вектор из вершины к центру окружности.

Если окружность находится внутри области ребра, то ближайшая к центру окружности точка отрезка будет проекцией центра окружности на отрезок. Нормаль коллизии будет просто нормалью к ребру.

Чтобы вычислить, в какой из областей Вороного лежит окружность, мы используем скалярное произведением между парой вершин. Идея заключается в том, чтобы создать воображаемый треугольник для проверки того, больше или меньше 90 градусов угол, созданный с вершиной отрезка. Для каждой вершины отрезка прямой создаётся по одному треугольнику.

Проецируем на ребро вектор из вершины ребра к центру окружности.

Значение больше 90 градусов будет значить, что область ребра найдена. Если ни у одного из треугольников нет углов при вершине ребра больше 90 градусов, то для генерирования информации многообразия центр окружности нужно спроецировать на сам отрезок. Как показано на рисунке выше, если при скалярном умножении вектора из вершины ребра к центру окружности на сам вектор ребра получается отрицательное значение, то область Вороного, в которой лежит окружность, нам известна.

К счастью, скалярное произведение можно использовать для вычисления проекции со знаком. Этот знак будет отрицательным, если угол больше 90 градусов, и положительным, если меньше.

---

Разрешение коллизий

И этот момент снова настал: вернёмся к коду разрешения импульсов в третий и последний раз. К этому времени мы уже полностью освоились с написанием кода разрешения, вычисляющего импульсы силы вместе с импульсами силы трения, а также можем выполнить линейное проецирование для разрешения оставшегося проникновения.

К разрешению трения и проникновения необходимо добавить компоненты вращения. В угловую скорость нужно добавить энергию.

Вот разрешение импульсов силы в том виде, в котором мы оставили его в предыдущей части про трение:

Если мы добавим компоненты вращения, то конечное уравнение будет выглядеть так:

В приведённом выше уравнении — это снова «радиус», как в векторе из ЦМ объекта к точке контакта. Это уравнение подробно выводится на сайте Криса Хекера.

Важно понимать, что скорость заданной точки объекта равна:

С учётом условий вращения приложение импульсов силы немного изменилось:

void Body::ApplyImpulse( const Vec2& impulse, const Vec2& contactVector )
{
  velocity += 1.0f / mass * impulse;
  angularVelocity += 1.0f / inertia * Cross( contactVector, impulse );
}

---

Заключение

На этом последняя часть туториала завершается. Мы рассмотрели довольно небольшое количество тем, включая разрешение импульсов силы, генерирование многообразий, трение и ориентация в двух измерениях.

Если вы добрались до конца, то я поздравляю вас! Программирование физических движков для игр — невероятно сложная для изучения область, желаю всем читателям удачи.

Автор: PatientZero

Источник