
Если вы программист, то, возможно, у вас возникали ситуации, когда в выбранном игровом движке или библиотеке нет нужной функции. За этим следовал ужасающий момент, когда вам приходилось обыскивать весь Интернет в поисках кода, написанного людьми, решавшими эту проблему до вас (я говорю о вас, пользователи StackOverflow). Конечно, в этом нет ничего плохого (я и сам так поступаю), но очень часто вы можете сделать это самостоятельно, даже когда речь идёт о таких теоретических задачах, как геометрия или перетасовка. Я один из тех людей, которые всегда пытаются понять, как всё работает, и разве есть способ понимания лучше, чем прийти к нему самому, заново изобретя решение на лету (если, конечно, оно существует)?
Ставим перед собой пример задачи
В этой статье я опишу несколько этапов, которые, как мне кажется, довольно эффективны для самостоятельного выведения решающего задачу алгоритма. Чтобы применить их к чему-то конкретному, мы рассмотрим пример задачи: выпуклое разбиение простых многоугольников. Это звучит сложно и по-научному, но на самом деле это не так трудно.
Простой многоугольник — это многоугольник, который не пересекает сам себя и не имеет отверстий. Выпуклый многоугольник — это тот, в котором все углы меньше 180°. Разумеется, выпуклый многоугольник является простым многоугольником, а простой многоугольник — это сложный многоугольник (наиболее общий класс многоугольников), однако обратное не всегда верно.
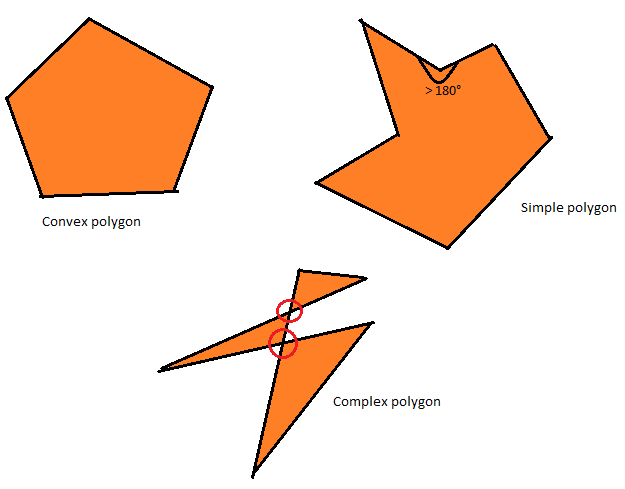
Выпуклый, простой и сложный многоугольники.
Очень хорошее свойство выпуклых многоугольников заключается в том, что проверка коллизий между двумя произвольными выпуклыми многоугольниками очень проста (мы не будем рассматривать это в статье), в то время как проверка коллизий между двумя произвольными сложными, или даже простыми многоугольниками неприлично сложна. И здесь в дело вступает выпуклое разбиение: если мы сможем разделить простой многоугольник на несколько меньших выпуклых многоугольников, то коллизия с ним аналогична коллизии по крайней мере с одним многоугольником из разбиения. Поэтому наш пример задачи будет таким: имея массив точек, описывающих простой многоугольник, вернуть массив массивов, описывающий выпуклые многоугольники, «в сумме» дающие исходный многоугольник.
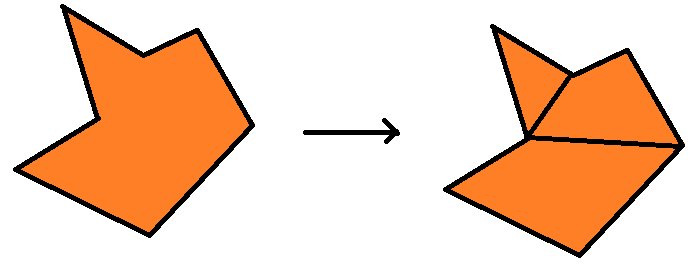
В идеале наш алгоритм должен уметь выполнять такую операцию.
Изучи то, с чем работаешь
При разработке алгоритмов самое важное — опознать задачу, которую хочешь решить, то есть то, что в первую очередь должен делать алгоритм. Может это и звучит глупо, но важнее не то, как должен работать алгоритм, а то, что он должен получать на входе и выдавать на выходе (в том числе и структуры данных, если это необходимо). Чаще всего знание структур данных, с которыми вам предстоит работать, помогает сформулировать свои рассуждения. Например, если вы создаёте алгоритм сортировки, то есть вероятность, что на входе он будет получать массив, но что должно быть на выходе: новый массив, ничего или сортировка на месте (непосредственное изменение самого исходного массива)?
Прочитайте мою предыдущую статью про алгоритм для кривых, это хороший пример алгоритма, входные и выходные данные которого довольно сложно характеризировать. На самом деле, можно сказать, что алгоритм на входе получает функцию числа с плавающей запятой и целого числа, где функция описывает параметрическую кривую, а целое числое — количество этапов сэмплирования. Алгоритм должен возвращать на выходе другую функцию числа с плавающей запятой, то есть функцию «кривой», которой посвящена статья, и она, в сущности является более обычной версией исходной кривой.
В нашем примере задачи, как уже сказано выше, алгоритм будет получать на входе массив точек и возвращать на выходе массив массивов точек. Входными данными будут вершины простого многоугольника, а выходными данными будут вершины всех выпуклых многоугольников в выпуклом разбиении исходного многоугольника.
В первую очередь — мозг и бумага
Начинать с бумаги и карандаша (или ручки, если вы любите рисковать) — один из лучших способов восприятия задачи, и это относится не только к созданию алгоритмов (и даже не только к программированию). Разумеется, программирование — не исключение, поэтому давайте приступим и начнём с самого начала.
Во-первых, для разработки интуитивного подхода чаще всего стоит начинать с зарисовки (или записывания, в зависимости от того, над чем вы работаете) простых случаев, которые вы можете решить самостоятельно, не особо задумываясь над тем, что вы делаете. В процессе этой работы или после него вам стоит проанализировать способ размышлений над ним и упорядочить его, разбив на этапы. Идея заключается в том, что, хотите вы этого или нет, вы выполняете алгоритм: ваш — тоже компьютер, самый мощный компьютер, известный человеку. Настолько мощный, что способен посмотреть на собственную работу и понять её; настолько мощный, что вы уже выполняете алгоритм, который пытаетесь записать, но почему-то пока не понимаете его (потому что ещё не осознали его!). Однако вы можете выполнить алгоритм шаг за шагом, чтобы понять, как он работает. Для проверки этой теории давайте вернёмся к нашему примеру задачи и воспользуемся тем самым простым многоугольником.
Рекомендую вам самим нарисовать такой многоугольник, и в этот момент прервать чтение, чтобы попытаться разделить этот многоугольник на меньшие фигуры таким образом, чтобы в них никогда не было внутренних углов больше 180°. Я показал моё решение на рисунке выше, но поскольку все думают по-разному, в конце у нас могут получиться другие фигуры. И это абсолютно нормально, на самом деле выпуклое разбиение простого многоугольника не уникально!

Оба этих разбиения являются выпуклыми.
После того, как мы за секунды применили алгоритм вычислительной геометрии, на самом деле не зная его, с помощью самого мощного в известной вселенной компьютера, мы можем обернуться назад и разбить алгоритм на этапы. Повторюсь, все мы мыслим по-разному, поэтому этапы могут отличаться: я применю его к своим рассуждениям, а ваши будут достаточно похожими.
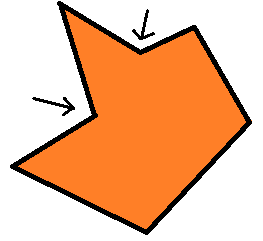
Во-первых, я задал себе вопрос: почему этот многоугольник ещё не выпуклый? Ответ пришёл довольно быстро: потому что некоторые из внутренних углов больше 180° (а именно два из них, показанные на рисунке стрелками), что по определению не даёт многоугольнику быть выпуклым. Чтобы исправить это, я затем подумал, что нужно разрезать угол, чтобы получить два меньших угла, которые в идеале будут не больше 180°. Этого можно достичь, соединив «дефектную» вершину с какой-нибудь другой вершиной многоугольника. Повторим это для всех дефектных вершин и получим наше выпуклое разбиение!

Пошаговое интуитивное выпуклое разбиение; стрелками показаны «дефектные» вершины.
Отлично, всё произошло довольно быстро. Но что же случилось на самом деле? На этом этапе мы можем записать зародыш алгоритма в псевдокоде, напоминающем естественный язык. Это не совсем предложение из языка, но и не совсем программирование. Оно просто выглядит достаточно похоже на программирование, чтобы запустить в
пока существует "дефектная" вершина
соединять её с другой вершиной многоугольника
конец пока
Из этого становится понятно, что нам нужен способ определить, является ли вершина «дефектной». Для этого достаточно просто проверить, образуют ли две составляющих вершину ребра угол больше 180°. Однако есть и другая, более серьёзная задача: какую вершину мы выбираем для соединения с дефектной вершиной? Давайте ещё раз подумаем, как мы делали это в прошлый раз.
Я делал это так: я стремился включить в каждый многоугольник как можно больше вершин, чтобы минимизировать количество многоугольников в разбиении. В общем случае это хорошая мысль, потому что эффективнее обрабатывать один прямоугольник, чем два треугольника, которые соединяются в прямоугольник — хотя они описывают одинаковую форму, у нас в одном случае получается четыре вершины, а в другом — шесть. Мы делаем это следующим образом: по порядку проверяем каждую вершину, начиная с дефектной, пока не найдём ту вершину, которая превращает наш многоугольник в невыпуклый, после чего мы выбираем последнюю вершину, в которой он оставался выпуклым. Это возможно всегда, потому что треугольник всегда является выпуклым, поэтому в наихудшем случае мы получим треугольник. Теперь наш псевдокод будет выглядеть так:
пока есть дефектная вершина
пока следующая вершина образует с дефектной вершиной угол 180° или меньше
перейти к следующей вершине
если угол, образованный этой новой вершиной больше 180°, остановиться и выбрать предыдущую
конец пока
соединить дефектную вершину с выбранной вершиной
конец пока
Но эта проверка может привести к паре сомнительных ситуаций: что, если вершина сразу после нашей дефектной вершины тоже является дефектной? Что, если в процессе проверки мы дойдём до дефектной вершины? Второй вопрос вроде бы решает себя благодаря тому наблюдению, что в выпуклом многоугольнике не может быть дефектных вершин, необходимо сразу же остановиться и выбрать её, чтобы ребро, которое мы добавляем при разбиении угла превратила её в «правильную» вершину. Первый вопрос можно решить интуитивно: когда мы решаем задачу вручную, этого никогда не происходит, потому что мы намеренно начинаем или с самой левой, или самой правой дефектной вершины, а очевидно не с той, которая находится между другими дефектными вершинами. В коде это просто преобразуется в то, что мы начинаем исследование с дефектной вершины, у которой точно есть правильный сосед. Это возможно всегда, потому что простой многоугольник всегда имеет хотя бы одну «правильную» (то есть недефектную) вершину. Найдите её, используйте, чтобы избавиться от одной дефектной вершины, повторите. Наш псевдокод теперь выглядит так:
пока есть дефектная вершина
выбрать ту, после которой есть "правильная" вершина
пока следующая вершина с дефектной вершиной образуют угол в 180° или меньше
перейти к следующей вершине
если эта новая вершина "неправильна", остановиться и выбрать её
иначе если угол, образованный этой новой вершиной больше 180°, остановиться и выбрать предыдущую вершину
конец пока
соединить дефектную вершину с выбранной вершиной
конец пока
И при выполнении код даст нам что-то подобное:
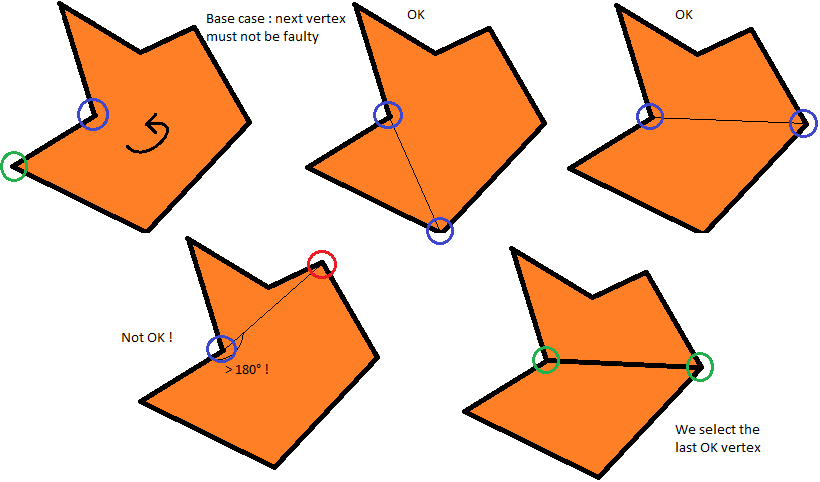
Один шаг алгоритма: выбор вершины, с которой нужно соединить дефектную вершину.
Выглядит довольно неплохо!
Остаётся ещё один вопрос: сейчас мы сохраняем наши многоугольники как массив вершин, а не рёбер, что же означает тогда «соединение вершин»? Мы не добавляем и не удаляем вершины из многоугольника, поэтому, наверно, не можем изменять массив вершин? Или можем?
Давайте посмотрим на то, как мы подходили к этому вопросу при работе вручную: после прорисовки ребра нам становится совершенно неинтересна часть, ставшая выпуклой, и мы сосредоточены только на оставшихся вершинах. Однако нас по-прежнему интересует только что добавленное ребро, и мы по-прежнему добавляем в поиск составляющие его вершины. У этого есть довольно чёткая интерпретация: мы просто разбиваем многоугольник на две части, выпуклую и простую, и нас перестаёт интересовать выпуклая часть при повторном применении алгоритма к новому, меньшему простому многоугольнику!
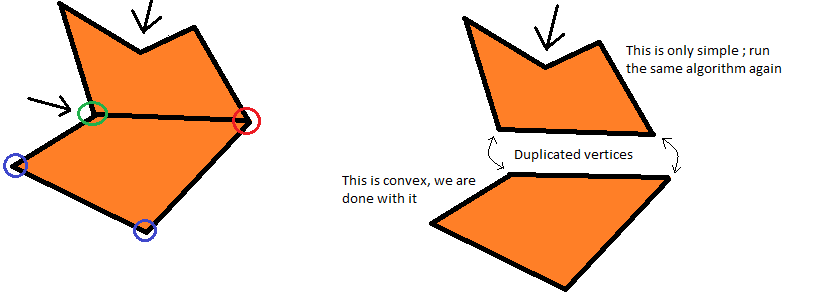
Теперь мы понимаем, что же означает «соединение»: в сущности, это создание нового многоугольника из всех вершин между начальной и конечной точками (а именно зелёной и красной на рисунке; «между» означает, что мы двигаемся по многоугольнику) с вычитанием этого многоугольника из исходного многоугольника с повторным вызовом алгоритма для получившейся меньшей группы вершин. Помните, что в обоих многоугольниках должны присутствовать обе вершины, составляющие добавляемое ребро!
Каждый раз, когда мы завершаем полную итерацию алгоритма и получаем одну выпуклую и одну простую части, мы должны добавить выпуклую часть в массив: это массив, который вернёт алгоритм после своего завершения, массив выпуклых компонентов исходного многоугольника. Что касается простой части, то, как вы уже догадались, для неё мы снова вызываем алгоритм.
Теперь наш псевдокод выглядит вот так:
function makeConvex
выбрать дефектную вершину, после которой есть "правильная" вершина
пока следующая вершина образует с дефектной угол в 180° или меньше
перейти к следующей вершине
если эта новая вершина "неправильна", остановиться и выбрать её
иначе если угол, образованный этой новой вершиной, больше 180°, остановиться и выбрать предыдущую вершину
конец пока
добавить в массив все вершины между дефектной вершиной и выбранной вершиной, включая их обе
удалить из исходного многоугольника все вершины между дефектной вершиной и выбранной вершиной, не включая их обе
вернуть выпуклый массив, конкатенированный с результатом функции makeConvex, вызванной для нового многоугольника
конец функции
И на этом всё, мы закончили! Наш этап работы с
Послесловие
Не забывайте, что псевдокод обеспечивает довольно наивный подход и он не оптимизирован. Смысл не в том, чтобы создать самый эффективный алгоритм, а в том, чтобы научиться создавать собственные. Придумывайте всё больше своих алгоритмов, и возможно однажды у вас появится правильная идея умного алгоритма, до которого не додумался никто другой. Если после прочтения этой статьи вы решили, что прежде, чем искать решение определённой задачи онлайн, стоит подумать о создании своего собственного решения, то я буду считать, что достиг своей цели.
Автор: PatientZero





