Введение
В публикации [1] подробно рассмотрена реализация на Python метода измерения отношения частот с использованием фигур Лиссажу. В качестве примера были проанализированы формы колебаний консольной эллиптической трубки вибрационного уровнемера [2].
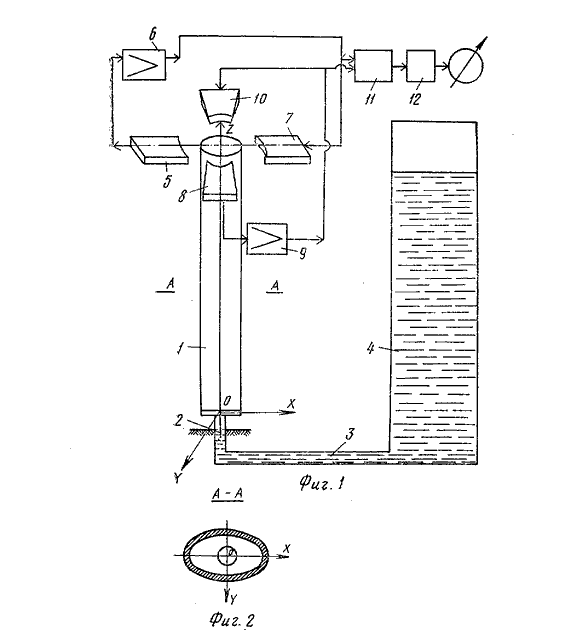
Упруго закреплённая трубка эллиптического сечения с помощью систем возбуждения 5,6,7 совершает автоколебания в одной плоскости, а с помощью систем 8, 9, 10 в другой плоскости перпендикулярной первой. Трубка колеблется в двух взаимно перпендикулярных плоскостях с разными частотами близкими к собственным. Масса трубки зависит от уровня заполняющей её жидкости.
С изменением массы меняются и частоты колебаний трубки, которые и являются выходными сигналами уровнемера. Частоты несут дополнительную информацию о мультипликативных и аддитивных дополнительных погрешностях, компенсируемых при обработке частот микропроцессором 11.
Остался не решённым вопрос определения зависимости частот колебаний трубки от уровня заполняющей жидкости что и является предметом данной публикации.
Постановка задачи
Определить частоты изгибных колебаний трубки в двух взаимно перпендикулярных плоскостях методом Релея с использованием точного уравнения изгибной линии трубки из публикации [1].
С использованием полученных соотношений для частот найти зависимости чувствительности от уровня и определить диапазоны пригодные для контроля уровня жидкости.
Для реализации указанных задач средствами Python рассмотреть два метода решения символьный и символьно-численный. Сравнить указанные методы по производительности
Применение метода Релея для определения частот колебаний консольной трубки эллиптического сечения
Суть метода Релея состоит в определении максимальной кинетической Tmax и максимальной потенциальной Pmax энергий консервативной колебательной системы с последующим приравниванием энергий Tmax= Pmax.
Из полученного уравнения можно найти частоту колебаний системы с учётом того, что все гармонические составляющие можно приравнять к максимальным значениям, например sin(t*w)**2=1 и cos(t*w)**2=1.
Символьное решение на Python
Применим следующее уравнение изгибной линии трубки:
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).
Запишем следующий листинг программы для расчёта кинетической энергии пустой трубки длинной L по функции –def fp(L), на первой форме колебаний при k=1.875:
def fp(L):
x,A, L, w, t, k =symbols('x A L w t k ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(t))**2
return factor(integrate(dx2,(x,0,L)))/(A**2*w**2*cos(t*w)**2)Для кинетической энергии жидкости, заполняющей трубку до уровня h и колеблющейся с трубкой как единое целое, вследствие малого сечения получим функцию def fh(h):
def fh(h):
x,A, h, w, t, k =symbols(' x A h w t k ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(t))**2
return factor(integrate (dx2,(x,0,h)))/(A**2*w**2*cos(t*w)**2)Для потенциальной энергии трубки функция def pl(L) будет иметь вид:
def pl(L):
x,A, J, w, t, k,L =symbols('x A J w t k L ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(x))**2
return factor(integrate (dx2,(x,0,L)))/(A**2*sin(t*w)**2)Теперь можно составить уравнение Релея– Tmax= Pmax.Для этого умножим функции def fp(L), def fh(h), def pl(L), на коэффициенты (A**2*w**2*cos(t*w) **2) и (A**2*sin(t*w) **2), на которые их делили в листингах. Зачем сначала делить, а потом умножать поясню позже, когда будем рассматривать символьно-численный метод.
Умножим функции кинетических энергий на массы единицы длины трубки и жидкости – m0 и m. Функцию потенциальной энергии умножим на жёсткость E*J. Решая уравнение Релея для круговой частоты – w, преобразовав её в циклическую –f=w/2*pi, получим:
f=(0.5/pi)*((pl(L))*(E*J)/(m0*fp(L)+m*fh(h)))**0.5
Имея функцию для частоты колебаний можно получить символьное решение.
from sympy import *
from numpy import arange,pi
import matplotlib.pyplot as plt
import time
start = time.time()
def fp(L):
x,A, L, w, t, k =symbols('x A L w t k ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(t))**2
return factor(integrate(dx2,(x,0,L)))/(A**2*w**2*cos(t*w)**2)
def fh(h):
x,A, h, w, t, k =symbols(' x A h w t k ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(t))**2
return factor(integrate (dx2,(x,0,h)))/(A**2*w**2*cos(t*w)**2)
def pl(L):
x,A, J, w, t, k,L =symbols('x A J w t k L ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(x))**2
return factor(integrate (dx2,(x,0,L)))/(A**2*sin(t*w)**2)
""" Установка численных значений символьных переменных """
L,h,m,m0,E,J,q =symbols(' L,h m0 m E J q ')
k1=q.subs({q:0.16})
k2=pl(L).subs({L:1})
k3=E.subs({E:196e9})*J.subs({J:2.3e-08})
k4=m0.subs({m0:1.005})
k5=m.subs({m:0.98})
k6=fp(L).subs({L:1})
"""Решения для частот чувствительностей к уровню и траекторий конца ттрубки """
x=arange(0.0,1.0,0.01)
f=k1*((k2+k3)/(k4*k6+k5*fh(h)))**0.5
y=[k1*((k2+k3)/(k4*k6+k5*fh(h).subs({h:w})))**0.5 for w in arange(0.0,1.0,0.01)]
s=f.diff(h)
y1=[s.subs({h:w}) for w in arange(0.0,1.0,0.01)]
k3=E.subs({E:196e9})*J.subs({J:1.7e-08})
f1=k1*((k2+k3)/(k4*k6+k5*fh(h)))**0.5
y2=[k1*((k2+k3)/(k4*k6+k5*fh(h).subs({h:w})))**0.5 for w in arange(0.0,1.0,0.01)]
s1=f1.diff(h)
y3=[s1.subs({h:w}) for w in arange(0.0,1.0,0.01)]
k7=fh(h).subs({h:0.7})
k3=E.subs({E:196e9})*J.subs({J:2.3e-08})
f1=k1*((k2+k3)/(k4*k6+k5*k7))**0.5
k3=E.subs({E:196e9})*J.subs({J:1.7e-08})
f2=k1*((k2+k3)/(k4*k6+k5*k7))**0.5
x1=[sin(f1*t) for t in arange(0.,2*pi,0.01)]
y4=[sin(f2*t) for t in arange(0.,2*pi,0.01)]
""" Построение графиков"""
plt.subplot(221)
plt.plot(x, y, label='f1-zox')
plt.plot(x, y2,label='f2- zoy')
plt.xlabel(' h')
plt.ylabel(' f 1,f2')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(222)
plt.plot(x, y1,label='s=df/dh zox')
plt.plot(x, y3,label='s1=df1/dh - zoy')
plt.ylabel('s')
plt.xlabel(' h ')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(223)
plt.plot(x1, y4,label='X,Y для h=0.7')
plt.ylabel(' Y')
plt.xlabel('X')
plt.grid(True)
plt.legend(loc='best')
stop = time.time()
print ("Время :",round(stop-start,3))
plt.show()
Результат:

Время: 165.868
Из полученных графиков видно, что измерение или контроль можно осуществлять с уровня 0.75 длинны L трубки для водных растворов. Самая высокая чувствительность на конце трубки.
Учитывая высокую стабильность частоты механического резонатора, порядка e-6, измерение можно осуществлять и на более широком участке от 0.5 L. А на участке от 0.75 L можно применить микропроцессорную обработку с компенсацией как аддитивной, так и мультипликативной составляющих погрешности.
Вывод
Символьное решение даёт хороший результат, но занимает много машинного времени.
Символьно -численное решение на Python
Можно получить символьное решение для функций def fp(L), def fh(h), def pl(L), поэтому мы и делили их на (A**2*w**2*cos(t*w) **2) и (A**2*sin(t*w) **2), чтобы сократить количество переменных до двух- L,h. А так же получить символьное решение для чувствительности уровнемера.
Это можно сделать с помощью следующего листинга:
from sympy import *
from numpy import arange,pi
import matplotlib.pyplot as plt
import time
start = time.time()
def fp(L):
x,A, L, w, t, k =symbols('x A L w t k ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(t))**2
return factor(integrate(dx2,(x,0,L)))/(A**2*w**2*cos(t*w)**2)
def fh(h):
x,A, h, w, t, k =symbols(' x A h w t k ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(t))**2
return factor(integrate (dx2,(x,0,h)))/(A**2*w**2*cos(t*w)**2)
def pl(L):
x,A, J, w, t, k,L =symbols('x A J w t k L ')
z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875})
dx=z*A*sin(w*t)
dx2=(dx.diff(x))**2
return factor(integrate (dx2,(x,0,L)))/(A**2*sin(t*w)**2)
L,h,m,m0,E,J,q =symbols(' L,h m0 m E J q ')
f=q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5
s=f.diff(h)
print(fp(L))
print(fh(h))
print(pl(L))
print(s)
stop = time.time()
print ("Время :",round(stop-start,3))
Время: 6.696
Листинг не нагружен многократными вычислениями функций, поэтому время его выполнения 6.696 с. Тем более его нужно использовать всего один раз.
Теперь остаётся скопировать результаты print(fp(L)), print(fh(h)), print(pl(L)), print(s) в соответствующие функции следующего листинга в котором удобно и быстро можно менять все исходные данные для расчёта. Результаты print не привожу, как и в предыдущих листингах, чтобы не загромождать текст.
from numpy import (pi,cos,cosh,sin,sinh,arange)
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import time
start = time.time()
L=1# длинна консольной трубки в м.
d=1e-3# толщина стенки в м.
e=0.8# эксцентриситет сечения б.р.
a0=20e-3# большая внутренняя полуось в м.
a=a0+d# большая наружная полуось в м.
b0=a0*e# малая внутренняя полуось в м.
b=b0+d#малая наружная полуось в м.
E=196e9# модуль Юнга материала в н/м2.
rm=7.9e3# массовая плотность материала трубки в кг/м3.
rg=1e3#массовая плотность жидкости в кг/м3.
J=(pi/4)*(a**3*b-a0**3*b0)# статический момент инерции по малой оси в м4.
J1=(pi/4)*(a*b**3-a0*b0**3)#статический момент инерции по большй оси в м4.
m0=pi*(a*b-a0*b0)*rm# масса единицы длинны трубки в кг/м3
m=pi*(a0*b0)*rg#масса единицы длинны жидкости в кг/м3
q=1/(2*pi)# коэффициент для перевода круговой частоты в циклическую
def fp(L):# функция кинитической энергии пустой консольной трубки L
return (1.83012983499975*L*sin(1.875*L)**2 + 1.83012983499975*L*cos(1.875*L)**2 - 0.830129834999752*L*sinh(1.875*L)**2 + 0.830129834999752*L*cosh(1.875*L)**2 - 0.869882798951083*sin(1.875*L)**2 + 0.442735911999868*sin(1.875*L)*cos(1.875*L) + 1.73976559790217*sin(1.875*L)*sinh(1.875*L) - 1.9521384906664*sin(1.875*L)*cosh(1.875*L) - 0.885471823999735*cos(1.875*L)*sinh(1.875*L) + 0.976069245333201*sinh(1.875*L)*cosh(1.875*L) - 0.869882798951083*cosh(1.875*L)**2 + 0.869882798951083)
def fh(h):# функция кинитической энергии жидкости уровня h
return (1.83012983499975*h*sin(1.875*h)**2 + 1.14978095631541e-15*h*sin(1.875*h)*sinh(1.875*h) + 1.83012983499975*h*cos(1.875*h)**2 - 1.07791964654569e-15*h*cos(1.875*h)*cosh(1.875*h) - 0.830129834999752*h*sinh(1.875*h)**2 + 0.830129834999752*h*cosh(1.875*h)**2 - 0.869882798951083*sin(1.875*h)**2 + 0.442735911999868*sin(1.875*h)*cos(1.875*h) + 1.73976559790217*sin(1.875*h)*sinh(1.875*h) - 1.9521384906664*sin(1.875*h)*cosh(1.875*h) - 0.885471823999735*cos(1.875*h)*sinh(1.875*h) + 0.976069245333201*sinh(1.875*h)*cosh(1.875*h) - 0.869882798951083*cosh(1.875*h)**2 + 0.869882798951083)
def pl(L):# функция потенциальной энергии консольной трубки жёсткостью E*J/L**3
return (6.434050201171*L*sin(1.875*L)**2 + 1.48843545191282e-15*L*sin(1.875*L)*sinh(1.875*L) + 6.434050201171*L*cos(1.875*L)**2 - 2.79081647233653e-15*L*cos(1.875*L)*cosh(1.875*L) + 2.918425201171*L*sinh(1.875*L)**2 - 2.918425201171*L*cosh(1.875*L)**2 + 3.0581817150624*sin(1.875*L)**2 - 1.55649344062453*sin(1.875*L)*cos(1.875*L) + 3.11298688124907*sin(1.875*L)*cosh(1.875*L) - 6.86298688124907*cos(1.875*L)*sinh(1.875*L) + 6.1163634301248*cos(1.875*L)*cosh(1.875*L) - 3.0581817150624*sinh(1.875*L)**2 + 3.43149344062453*sinh(1.875*L)*cosh(1.875*L) - 6.1163634301248)
def f(m0,q,E,J,h,m):# чувствительность уровнимера s=df/dh
return -0.5*m0*q*((E*J + 6.434050201171*L*sin(1.875*L)**2 + 6.434050201171*L*cos(1.875*L)**2 + 2.918425201171*L*sinh(1.875*L)**2 - 2.918425201171*L*cosh(1.875*L)**2 + 3.0581817150624*sin(1.875*L)**2 - 1.55649344062453*sin(1.875*L)*cos(1.875*L) + 3.11298688124907*sin(1.875*L)*cosh(1.875*L) - 6.86298688124907*cos(1.875*L)*sinh(1.875*L) + 6.1163634301248*cos(1.875*L)*cosh(1.875*L) - 3.0581817150624*sinh(1.875*L)**2 + 3.43149344062453*sinh(1.875*L)*cosh(1.875*L) - 6.1163634301248)/(m*(1.83012983499975*L*sin(1.875*L)**2 + 1.83012983499975*L*cos(1.875*L)**2 - 0.830129834999752*L*sinh(1.875*L)**2 + 0.830129834999752*L*cosh(1.875*L)**2 - 0.869882798951083*sin(1.875*L)**2 + 0.442735911999868*sin(1.875*L)*cos(1.875*L) + 1.73976559790217*sin(1.875*L)*sinh(1.875*L) - 1.9521384906664*sin(1.875*L)*cosh(1.875*L) - 0.885471823999735*cos(1.875*L)*sinh(1.875*L) - 0.869882798951083*sinh(1.875*L)**2 + 0.976069245333201*sinh(1.875*L)*cosh(1.875*L)) + m0*(1.83012983499975*h*sin(1.875*h)**2 + 1.83012983499975*h*cos(1.875*h)**2 - 0.830129834999752*h*sinh(1.875*h)**2 + 0.830129834999752*h*cosh(1.875*h)**2 - 0.869882798951083*sin(1.875*h)**2 + 0.442735911999868*sin(1.875*h)*cos(1.875*h) + 1.73976559790217*sin(1.875*h)*sinh(1.875*h) - 1.9521384906664*sin(1.875*h)*cosh(1.875*h) - 0.885471823999735*cos(1.875*h)*sinh(1.875*h) - 0.869882798951083*sinh(1.875*h)**2 + 0.976069245333201*sinh(1.875*h)*cosh(1.875*h))))**0.5*(1.0*sin(1.875*h)**2 - 3.26206049606656*sin(1.875*h)*cos(1.875*h) - 2.0*sin(1.875*h)*sinh(1.875*h) + 3.26206049606656*sin(1.875*h)*cosh(1.875*h) + 2.6602596699995*cos(1.875*h)**2 + 3.26206049606656*cos(1.875*h)*sinh(1.875*h) - 5.32051933999901*cos(1.875*h)*cosh(1.875*h) + 1.0*sinh(1.875*h)**2 - 3.26206049606656*sinh(1.875*h)*cosh(1.875*h) + 2.6602596699995*cosh(1.875*h)**2)/(m*(1.83012983499975*L*sin(1.875*L)**2 + 1.83012983499975*L*cos(1.875*L)**2 - 0.830129834999752*L*sinh(1.875*L)**2 + 0.830129834999752*L*cosh(1.875*L)**2 - 0.869882798951083*sin(1.875*L)**2 + 0.442735911999868*sin(1.875*L)*cos(1.875*L) + 1.73976559790217*sin(1.875*L)*sinh(1.875*L) - 1.9521384906664*sin(1.875*L)*cosh(1.875*L) - 0.885471823999735*cos(1.875*L)*sinh(1.875*L) - 0.869882798951083*sinh(1.875*L)**2 + 0.976069245333201*sinh(1.875*L)*cosh(1.875*L)) + m0*(1.83012983499975*h*sin(1.875*h)**2 + 1.83012983499975*h*cos(1.875*h)**2 - 0.830129834999752*h*sinh(1.875*h)**2 + 0.830129834999752*h*cosh(1.875*h)**2 - 0.869882798951083*sin(1.875*h)**2 + 0.442735911999868*sin(1.875*h)*cos(1.875*h) + 1.73976559790217*sin(1.875*h)*sinh(1.875*h) - 1.9521384906664*sin(1.875*h)*cosh(1.875*h) - 0.885471823999735*cos(1.875*h)*sinh(1.875*h) - 0.869882798951083*sinh(1.875*h)**2 + 0.976069245333201*sinh(1.875*h)*cosh(1.875*h)))
"""Графический анализ результатов"""
x=arange(0.0,1.0,0.01)
y1=[q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 for h in arange(0.0,1.0,0.01)] #числовая функция частоты трубки в сечении ZOX
J=(pi/4)*(a*b**3-a0*b0**3)#момент инерции в плоскости ZOY
y2=[q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 for h in arange(0.0,1.0,0.01)]#числовая функция частоты трубки в сечении ZOX
J=(pi/4)*(a**3*b-a0**3*b0)#момент инерции в плоскости ZOX
y3=[f(m0,q,E,J,h,m) for h in arange(0.0,1.0,0.01)]#числовая функция чувствительности трубки в сечении ZOX
J=(pi/4)*(a*b**3-a0*b0**3)#момент инерции в плоскости ZOY
y4=[f(m0,q,E,J,h,m) for h in arange(0.0,1.0,0.01)]#числовая функция чувствительности трубки в сечении ZOX
J=(pi/4)*(a**3*b-a0**3*b0)#момент инерции в плоскости ZOX
h=0.7
f1=q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 # частота колебаний для h=0.7 в плоскости ZOX
J=(pi/4)*(a*b**3-a0*b0**3)#момент инерции в плоскости ZOY
f2=q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 # частота колебаний для h=0.7 в плоскости ZOY
x1=[sin(f1*t) for t in arange(0.,2*pi,0.01)]#траектория конца трубки по Х
y5=[sin(f2*t) for t in arange(0.,2*pi,0.01)]#траектория конца трубки по Y
""" Построение графиков"""
plt.subplot(221)
plt.plot(x, y1, label='f-ZOX')
plt.plot(x, y2,label='f1-ZOY')
plt.xlabel(' h')
plt.ylabel(' f 1,f2')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(222)
plt.plot(x, y3,label='s1=df1/dh - ZOX')
plt.plot(x, y4,label='s2=df2/dh - ZOY')
plt.ylabel('s')
plt.xlabel(' h ')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(223)
plt.plot(x1, y5,label='X,Y для h=0.7')
plt.ylabel(' Y')
plt.xlabel('X')
plt.grid(True)
plt.legend(loc='best')
stop = time.time()
print ("Время :",round(stop-start,3))
plt.show()
Результат:
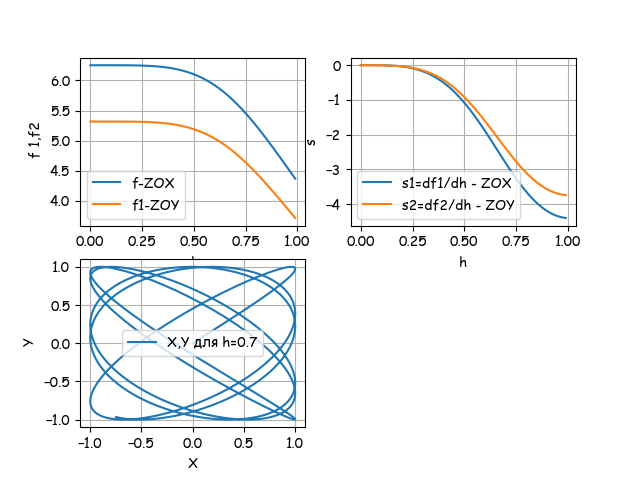
Время: 0.447
Таким образом получили тот же результат что и символьным методом, но уже в 165.868/0.447=371 раз быстрее.
Поверхность по которой колеблется трубка на первой форме её изгибных колебаний
#!/usr/bin/env python
#coding=utf8
import pylab
import numpy
from numpy import (zeros,arange,ones,pi,sin,cos,sinh,cosh)
from matplotlib.colors import LinearSegmentedColormap
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
def trubka():
a=10;b=10;k=q[0]
v = arange(0, 2.05*pi, 0.05*pi)
u= zeros([len(v),1])
for i in arange(0,len(v)):
u[i,0]=[sin(k*w)-sinh(k*w)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*w)-cosh(k *w) )for w in arange(0, 2.05*pi, 0.05*pi)][i]
x=a*u*cos(v)
y=b*u*sin(v)
z=u*ones(len(v))
return x,y,z
x,y,z=trubka()
fig = pylab.figure()
axes = Axes3D(fig)
axes.plot_surface(x, y, z, rstride=4, cstride=4, cmap = cm.jet)
pylab.show()
Результат:

Выводы:
Определены частоты изгибных колебаний трубки в двух взаимно перпендикулярных плоскостях методом Релея с использованием точного уравнения изгибной линии трубки.
С использованием полученных соотношений для частот найдены зависимости чувствительности от уровня и определены диапазоны пригодные для контроля или измерения уровня жидкости.
Для реализации указанных задач средствами Python рассмотрены два метода решения символьный и символьно-численный. Символьно-численный метод выполняется в 370 раз быстрее чем символьный.
Ссылки:
1. От двух камертонов из опытов Лиссажу к одной эллиптической уровнемерной трубке с шагом в столетия и всё на Python.
2. Вибрационный уровнемер.А.С.№777455
Автор: Scorobey






