
Под катом будем разбираться нужен ли для индексации интервалов специальный индекс, как быть с многомерными интервалами, правда ли что с 2-мерным прямоугольником можно обращаться как с 4-мерной точкой и т.д. Всё это на примере PostgreSQL.
В развитие темы (1, 2, 3, 4, 5, 6, 7).
Иногда данные представлены не значениями, а, скажем, интервалом достоверности. Или это действительно интервалы значений. Опять же, прямоугольник — тоже интервал, только не одномерный. Есть ли возможность за логарифмическое время проверить наличие в данных интервалов, пересекающиеся с искомым?
Да, конечно. Иногда для этого придумывают хитроумные схемы с вычислением и индексацией блочных (с дальнейшей точной фильтрацией) значений на основе, например, кодов Грея. При этом интервал с потерей точности кодируется в некоторое (индексируемое) число, при поиске интервал порождает набор значений (подинтервалов), которые следует проверить. Набор этот ограничен логарифмом.
А вот GiST умеет использовать для индексации временнЫх интервалов (tsrange) R-деревья.
create table reservations(during tsrange);
insert into reservations(during) values
('[2016-12-30, 2017-01-09)'),
('[2017-02-23, 2017-02-27)'),
('[2017-04-29, 2017-05-02)');
create index on reservations using gist(during);
select * from reservations where during && '[2017-01-01, 2017-04-01)';
Конечно же, автор с его крестовым походом против R-деревьев любовью к многомерным индексам не мог пройти мимо такой темы.
Итак, каким образом R-дерево справляется с интервалами? Так же как с и другими пространственными объектами. Интервал — это одномерный прямоугольник, при расщеплении страницы R-дерево старается минимизировать дисперсию внутри страниц-потомков и максимизировать оную между ними.
А можно ли интервал превратить в точку? Считая, например, его начало за X, а конец за Y. Формально можно, в конце концов, кто может запретить нам использовать два числа в качестве двумерной точки? Но в таких данных возникнет внутренняя зависимость. А семантика в данных приведет к семантике в поисковых запросах и интерпретации результатов.
Проще всего разобраться в ситуации, поглядев на неё глазами.
Вот 100 случайных интервалов размером от 0 до 10 000 с началом интервала от 0 до 100 000
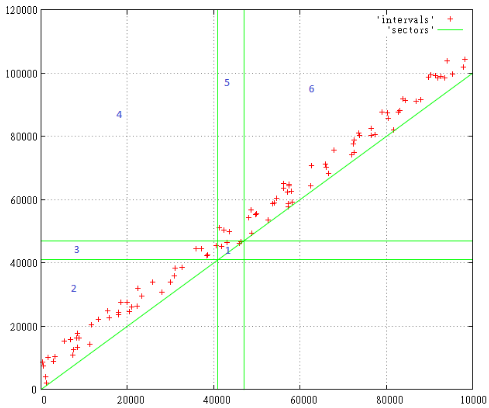
Фиг.1
Поисковый запрос — [41 000… 47 000], нас интересуют все интервалы, пересекающиеся с заданным диапазоном.
Цифрами отмечены зоны поиска, которые при этом возникают. Всё что ниже диагонали по понятным причинам не существует.
Итак, по зонам:
- сюда попадают интервалы, которые находятся строго внутри поискового запроса
- здесь всё, что началось и закончилось до нужного нам интервала
- эти интервалы начались до, а закончились во время поискового запроса
- здесь те интервалы, которые целиком покрывают поисковый
- эти интервалы начались во время, а закончились после запроса
- здесь всё, что началось и закончилось после него
Таким образом, для поиска всех пересечений запрос надо расширить до [0...47 000, 41 000… 100 000], т.е. он должен включать зоны 1,3,4,5.
То, что запрос стал размером с четверть всего слоя не должно пугать, ведь населена лишь узкая полоска вдоль диагонали. Да, могут быть быть большие интервалы размером с весь слой, но их относительно мало.
Конечно, большие объекты скажутся на производительности, но с этим ничего нельзя поделать, ведь они действительно существуют и действительно должны попадать в выдачу почти любого запроса. Если попытаться проиндексировать “макаронного монстра”, индекс фактически перестанет работать, дешевле будет просмотреть таблицу и отфильтровать лишнее.
Впрочем, по-видимому, любой метод индексации болеет от таких данных.
Есть ли еще какие-то минусы у такого подхода? Поскольку данные в некотором роде «выродились”, возможно, эвристика расщепления страниц R-дерева будет менее эффективна. Но самое большое неудобство в том, что надо постоянно иметь в виду, что мы имеем дело с интервалом и правильно задавать поисковые запросы.
Впрочем, это уже относится не к R-дереву, а к любому пространственному индексу. В том числе и Z-curve (построенному на Z-order B-дереву), использованному нами ранее. Для Z-curve не имеет значение вырождение данных, ведь это просто числа с их естественным порядком.
Помимо прочего, Z-curve еще и компактнее R-дерева. Поэтому попробуем прояснить его перспективы в обозначенной области.
Вот например, мы приняли, что X-координата — это начало сегмента, а Y-его конец. А что если наоборот? R-дереву должно быть всё равно, для Z-curve тоже мало что изменится. Обход страниц будет организован по-другому, но число прочитанных страниц в среднем окажется тем же.
Как насчет зеркально отобразить данные по одной из осей. В конце концов, у нас же Z-кривая (зеркально отображенная по Y), вот пусть данные и лягут на косую перекладину буквы Z. Хорошо, проведем численный эксперимент.
Возьмем 1000 случайных интервалов и разобьем их на 10 страниц в зависимости от Z-значения. Т.е. отсортируем и поделим по 100 штук, после посмотрим что у нас получилось. Приготовим 2 набора — X,Y и max(X)-X, Y
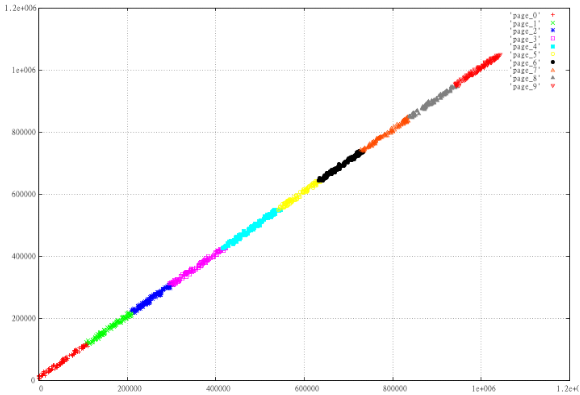
Фиг.2 Обычная Z-curve
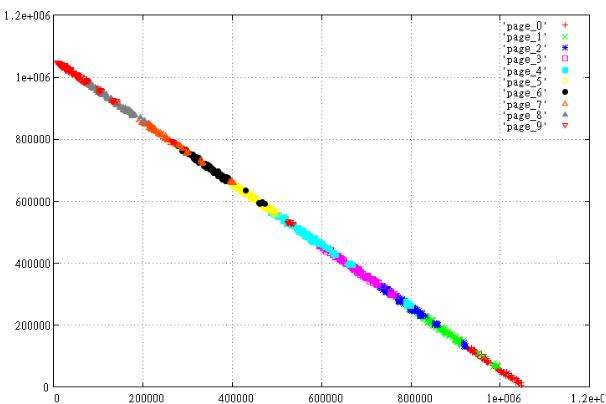
Фиг.3 Зеркально отображенные данные.
Прекрасно видно, насколько “хуже” устроены отображенные данные, страницы наползают друг на друга, периметр страниц намного больше, а это гарантия того, что в среднем при прочих равных такой вариант будет читать больше страниц.
Почему так получилось? В данном случае причина лежит на поверхности. Для 2-мерного прямоугольника Z-value левого нижнего угла <= чем для правого верхнего. Поэтому идеальный способ поаккуратнее порезать на страницы почти линейные данные — расположить их вдоль прямой X=Y.
А если индексировать не начало-конец диапазона, а его центр-длину? В этом случае данные вытянутся вдоль оси X, как если бы мы повернули Фиг.2 по часовой стрелке на 45 градусов. Проблема в том, что при этом и поисковая область тоже повернется на 45 градусов и по ней уже нельзя будет искать единым запросом.
Можно ли так индексировать интервалы с более чем одной размерностью? Конечно. 2-мерный прямоугольник превращается в 4-мерную точку. Главное не забывать, в какую из координат что мы положили.
Можно ли смешивать интервалы с неинтервальными значениями? Да, ведь алгоритм поиска по Z-curve не знает семантики значений, он работает с безликими числами. Если поисковый экстент задан в соответствии с этой семантикой и интерпретация результатов идёт с её учетом, никаких проблем не возникает.
Численный эксперимент
Попробуем проверить работоспособность Z-curve в условиях, приближенных к “макаронному монстру”. Модель данных такова:
- 8-мерный индекс, работоспособность и производительность которого мы уже проверяли
- как обычно, 100 млн точек
- объекты — 3-х мерные параллелепипеды — занимают 6 размерностей
- оставшиеся 2 размерности мы отдадим под интервал времени
- параллелепипедов 100 штук — они образуют по X&Y решетку 10Х10
- каждый параллелепипед живёт одну единицу времени
- за каждую единицу времени параллелепипед вырастает на 10 единиц по Z, начиная с высоты 0
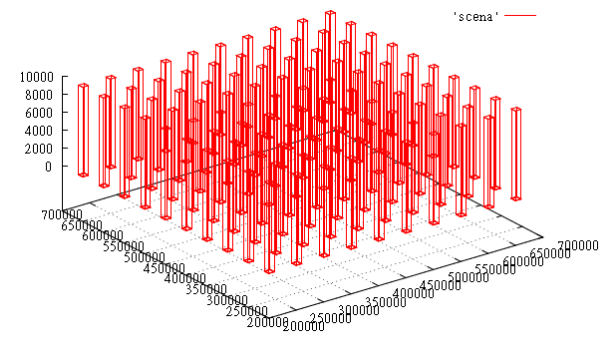
Фиг.4 срез данных в момент времени T=1000
На этом тесте проверим индексацию протяженных объектов, как она сказывается на производительности поиска.
Создаем 8-мерную таблицу, заливаем данные и индексируем
create table test_points_8d (p integer[8]);
COPY test_points_8d from '/home/.../data.csv';
create index zcurve_test_points_8d on test_points_8d (zcurve_num_from_8coords (p[1], p[2], p[3], p[4], p[5], p[6], p[7], p[8]));
Порядок ключа: xmax,xmin,ymax,ymin,zmax,zmin,tmax,tmin
файл данных (data.csv):
{210000,200000,210000,200000,0,0,0,0}
{210000,200000,210000,200000,10,0,1,1}
{210000,200000,210000,200000,20,0,2,2}
{210000,200000,210000,200000,30,0,3,3}
{210000,200000,210000,200000,40,0,4,4}
{210000,200000,210000,200000,50,0,5,5}
{210000,200000,210000,200000,60,0,6,6}
{210000,200000,210000,200000,70,0,7,7}
{210000,200000,210000,200000,80,0,8,8}
{210000,200000,210000,200000,90,0,9,9}
...Тестовый запрос [200 000...300 000; 200 000 … 300 000; 100...1000; 10...11]:
select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row
from zcurve_8d_lookup_tidonly('zcurve_test_points_8d',
200000,0,200000,0,100,0,10,0,
1000000,300000,1000000,300000,1000000,1000,1000000,11
) as c) x;Ответ:
c | t_row
-------------+-------------------------------------------
(0,11) | {210000,200000,210000,200000,100,0,10,10}
(0,12) | {210000,200000,210000,200000,110,0,11,11}
(103092,87) | {260000,250000,210000,200000,100,0,10,10}
(103092,88) | {260000,250000,210000,200000,110,0,11,11}
(10309,38) | {210000,200000,260000,250000,100,0,10,10}
(10309,39) | {210000,200000,260000,250000,110,0,11,11}
(113402,17) | {260000,250000,260000,250000,100,0,10,10}
(113402,18) | {260000,250000,260000,250000,110,0,11,11}
(206185,66) | {310000,300000,210000,200000,100,0,10,10}
(206185,67) | {310000,300000,210000,200000,110,0,11,11}
(216494,93) | {310000,300000,260000,250000,100,0,10,10}
(216494,94) | {310000,300000,260000,250000,110,0,11,11}
(20618,65) | {210000,200000,310000,300000,100,0,10,10}
(20618,66) | {210000,200000,310000,300000,110,0,11,11}
(123711,44) | {260000,250000,310000,300000,100,0,10,10}
(123711,45) | {260000,250000,310000,300000,110,0,11,11}
(226804,23) | {310000,300000,310000,300000,100,0,10,10}
(226804,24) | {310000,300000,310000,300000,110,0,11,11}
(18 rows)Чем хороша такая модель данных, можно легко оценить правильность результата.
На свеже-поднятом сервере тот же запрос через EXPLAIN (ANALYZE,BUFFERS)
показывает,: что была прочитана 501 страница.
Ок, пошевелим индекс. А что если посмотреть тот же запрос на индексе с порядком ключа — xmin,ymin,zmin,xmax,ymax,zmax,tmin,tmax. Запуск показывает 531 чтение. Многовато.
Хорошо, устраним геометрический перекос, пусть теперь колонны растут не на 10, а на 1 единицу за такт. Запрос (ключ: xmax,xmin,ymax,ymin,zmax,zmin,tmax,tmin)
EXPLAIN (ANALYZE,BUFFERS) select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row
from zcurve_8d_lookup_tidonly('zcurve_test_points_8d',
200000,0,200000,0,0,0,10,0,
1000000,300000,1000000,300000,1000000,1000,1000000,11) as c) x;говорит, что было прочитано 156 страниц!
Теперь немного статистики, посмотрим среднее число чтений/попаданий в кэш для разных типов ключей в серии из 10 000 случайных запросов
размером 100 000Х100 000Х100 000Х10
При порядке ключа —
(xmin,1 000 000-xmax, ymin,1 000 000-ymax,zmin,1 000 000-zmax,tmin,1 000 000-tmax)
Среднее число чтений — 21.8217, попаданий в кэш — 2437.51.
При этом среднее число объектов в выдаче — 17.81
При порядке ключа — (xmax,xmin,ymax,ymin,zmax,zmin,tmax,tmin)
Среднее число чтений — 14.2434, попаданий в кэш — 1057.19.
При этом среднее число объектов в выдаче — 17.81
При порядке ключа — (xmin,xmax,ymin,ymax,zmin,zmax,tmin,tmax)
Среднее число чтений — 14.0774, попаданий в кэш — 1053.22.
При этом среднее число объектов в выдаче — 17.81
Как видим, кэш страниц в данном случае работает весьма эффективно. Такое число чтений уже приемлемо.
И напоследок посмотрим глазами, просто из любопытства, как алгоритм Z-curve справляется с 8-мерным пространством.
Ниже представлены проекции разбора запроса в экстенте —
[200 000...300 000; 200 000 … 300 000; 0...700 001; 700 000...700 001].
Всего 18 результатов, 1687 подзапросов. Показаны порождённые подзапросы, зелёные крестики — чтения в B-дереве, синие крестики — найденные результаты.
Под каждым крестиком может скрываться несколько отметок. Близкорасположенные отметки сливаются, например время 700 000 и 700 001.
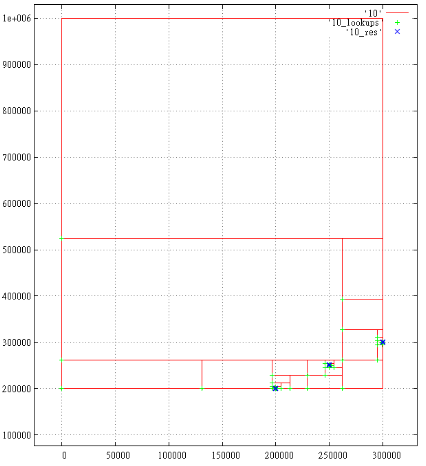
Фиг.5 X-ось
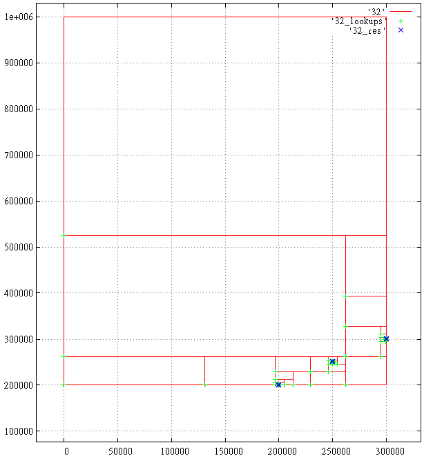
Фиг.6 Y-ось
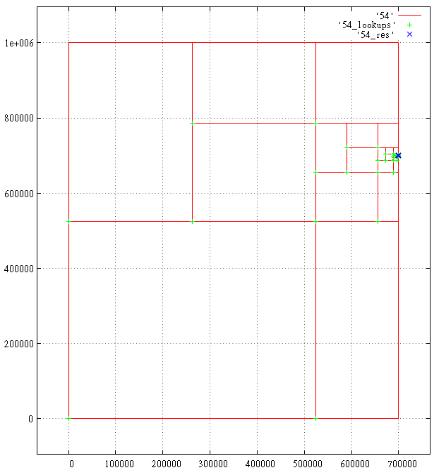
Фиг.7 Z-ось
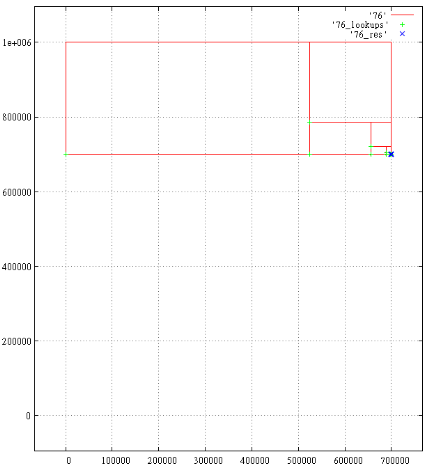
Фиг.8 Время
Автор: Борис Муратшин
