Сегментация лица на селфи без нейросетей

в 11:08, , рубрики: classic, cv2, dlib, face, no deep learning, opencv, python, segmentation, selfie, Алгоритмы, Блог компании Open Data Science, машинное обучение, обработка изображений

Сегментация лица на селфи без нейросетей - 1 Приветствую вас, коллеги. Оказывается, не все компьютерное зрение сегодня делается с использованием нейронных сетей. Хотя многие стартапы и заявляют, что у них дип лернинг везде, спешу вас разочаровать, они просто хотят хайпануть немножечко. Рассмотрим, например, задачу сегментации. В нашем слаке развернулась целая драма. Одна богатая и высокотехнологичная селфи-компания собрала датасет для сегментации селфи с помощью нейросетей (а это непростое и недешевое занятие). А другая, более бедная и не очень развитая решила, что можно подкупить людей, размечающих фотки, и спполучить базу. В общем, страсти в этих ваших Интернетах еще те. Недавно я наткнулся на статью, где без всяких нейросетей на устройстве делают очень даже хорошую сегментацию. Для сегментации от пользователя требуется дать алгоритму несколько подсказок, но с помощью dlib и opencv такие подсказки легко автоматизируются. В качестве бонуса мы так же сгладим вырезанное лицо и перенесем на какого-нибудь рандомного человека, тем самым поймем, как работают маски во всех этих снапчятах и маскарадах. В общем, классика еще жива, и если вы хотите немного окунуться в классическое компьютерное зрение на питоне, то добро пожаловать под кат.

Алгоритм

Кратко опишем алгоритм, а затем перейдем к его реализации по шагам. Допустим, у нас есть некоторое изображение, мы просим пользователя нарисовать на изображении две кривых. Первая (синий цвет) должна полностью принадлежать объекту интереса. Вторая (зеленый цвет) должна касаться только фона изображения.

Сегментация лица на селфи без нейросетей - 2

Далее делаем следующие шаги:

  • строим плотности распределения цветов точек для фона и для объекта;
  • для каждой точки вне штрихов вычисляется вероятность принадлежности к фону и к объекту;
  • используем эти вероятности для вычисления "расстояния" между точками и запускаем алгоритм поиска кратчайших расстояний на графе.
    В итоге точки, которые ближе к объекту, относим к нему и, соотвественно, те, что ближе к фону, относим к фону.

Дальнейший материал будет разбавляться вставками кода на питоне, если вы планируете выполнять его по мере чтения поста, то вам понадобятся следующие импорты:

import

%matplotlib inline
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("dark")
plt.rcParams['figure.figsize'] = 16, 12
import pandas as pd
from PIL import Image
from tqdm import tqdm_notebook
from skimage import transform
import itertools as it
from sklearn.neighbors.kde import KernelDensity
import matplotlib.cm as cm
import queue
from skimage import morphology
import dlib
import cv2
from imutils import face_utils
from scipy.spatial import Delaunay

Автоматизируем штрихи

Сегментация лица на селфи без нейросетей - 3 Идея того, как автоматизировать штрихи была навеяна приложением FaceApp, которое якобы использует нейросети для трансформации. Как мне кажется, они если и используют сети где то, то только в детектировании особых точек на лице. Взгляните на скриншот справа, они предлагают выровнять свое лицо по контуру. Вероятно, алгоритм детекции обучен примерно на таком масштабе. Как только лицо попадает в контур, сама рамка контура исчезает, значит особые точки вычислились. Позвольте вам представить сегодняшнего подопытного, а так-же напомнить, что из себя представляют эти самые особые точки на лице. 

img_input = np.array(Image.open('./../data/input2.jpg'))[:500, 400:, :]
print(img_input.shape)
plt.imshow(img_input)

Сегментация лица на селфи без нейросетей - 4

Теперь воспользуемся возможностями бесплатного программного обеспечения с открытым исходным кодом и найдем рамку вокруг лица и особые точки на лице, всего их 62.

# инстанцируем класс для детекции лиц (рамка)
detector = dlib.get_frontal_face_detector()
# инстанцируем класс для детекции ключевых точек
predictor = dlib.shape_predictor('./../data/shape_predictor_68_face_landmarks.dat')

# конвертируем изображение в много оттенков серого
img_gray = cv2.cvtColor(img_input, cv2.COLOR_BGR2GRAY)
# вычисляем список рамок на каждое найденное лицо
rects = detector(img_gray, 0)
# вычисляем ключевые точки
shape = predictor(img_gray, rects[0])
shape = face_utils.shape_to_np(shape)

отрисуем ключевые точки

img_tmp = img_input.copy()
for x, y in shape:
    cv2.circle(img_tmp, (x, y), 1, (0, 0, 255), -1)
plt.imshow(img_tmp)

Сегментация лица на селфи без нейросетей - 5

Оригинальная рамка на лице слишком мелкая (зеленый цвет), нам понадобится рамка, которая полностью содержит в себе лицо с некоторым зазором (красный цвет). Коэффициенты расширения рамки получены эмпирическим путем с помощью анализа нескольких десятков селфи разного масштаба и разных людей.

# оригинальная рамка
face_origin = sorted([(t.width()*t.height(), 
                       (t.left(), t.top(), t.width(), t.height())) 
                      for t in rects], 
                     key=lambda t: t[0], reverse=True)[0][1]

# коэффициенты расширения рамки
rescale = (1.3, 2.2, 1.3, 1.3)
# расширение рамки, так чтобы она не вылезла за края
(x, y, w, h) = face_origin
cx = x + w/2
cy = y + h/2
w = min(img_input.shape[1] - x, int(w/2 + rescale[2]*w/2))
h = min(img_input.shape[0] - y, int(h/2 + rescale[3]*h/2))
fx = max(0, int(x + w/2*(1 - rescale[0])))
fy = max(0, int(y + h/2*(1 - rescale[1])))
fw = min(img_input.shape[1] - fx, int(w - w/2*(1 - rescale[0])))
fh = min(img_input.shape[0] - fy, int(h - h/2*(1 - rescale[1])))

face = (fx, fy, fw, fh)

отрисовываем рамки

img_tmp = cv2.rectangle(img_input.copy(), (face[0], face[1]), 
                        (face[0] + face[2], face[1] + face[3]),
                        (255, 0, 0), thickness=3, lineType=8, shift=0)
img_tmp = cv2.rectangle(img_tmp, (face_origin[0], face_origin[1]), 
                        (face_origin[0] + face_origin[2], face_origin[1] + face_origin[3]),
                        (0, 255, 0), thickness=3, lineType=8, shift=0)
plt.imshow(img_tmp)

Сегментация лица на селфи без нейросетей - 6

Теперь у нас имеется область, которая точно не относится к лицу — всё, что вне красной рамки. Выберем оттуда некоторое количество случайных точек и будем считать их штрихами фона. Также у нас имеются 62 точки, которые точно расположены на лице. Для упрощения задачи я выберу 5 из них: по одной на уровне глаз на краю лица, по одной на уровне рта на краю лица и одну внизу посередине подбородка. Все точки внутри этого пятиугольника будут принадлежать только лицу. Опять же для простоты будем считать, что лицо вертикально расположено на изображении и потому мы можем отразить полученный пятиугольник по оси $y$, тем самым получив восьмиугольник. Все, что внутри восьмиугольника будем считать штрихом объекта. 

# выбираем вышеописанные пять точек
points = [shape[0].tolist(), shape[16].tolist()]
for ix in [4, 12, 8]:
    x, y = shape[ix].tolist()
    points.append((x, y))
    points.append((x, points[0][1] + points[0][1] - y))

# я не особо в прототипе запариваюсь над производительностью
# так что вызываю триангуляцию Делоне,
# чтобы использовать ее как тест на то, что точка внутри полигона
# все это можно делать быстрее, т.к. точный тест не нужен
# для прототипа :good-enough: 
hull = Delaunay(points)
xy_fg = []
for x, y in it.product(range(img_input.shape[0]), range(img_input.shape[1])):
    if hull.find_simplex([y, x]) >= 0:
        xy_fg.append((x, y))
print('xy_fg%:', len(xy_fg)/np.prod(img_input.shape))

# вычисляем количество точек для фона
# примерно равно что бы было тому, что на лице
r = face[1]*face[3]/np.prod(img_input.shape[:2])
print(r)
k = 0.1
xy_bg_n = int(k*np.prod(img_input.shape[:2]))
print(xy_bg_n)

# накидываем случайные точки
xy_bg = zip(np.random.uniform(0, img_input.shape[0], size=xy_bg_n).astype(np.int),
            np.random.uniform(0, img_input.shape[1], size=xy_bg_n).astype(np.int))
xy_bg = list(xy_bg)
xy_bg = [(x, y) for (x, y) in xy_bg 
         if y < face[0] or y > face[0] + face[2] or x < face[1] or x > face[1] + face[3]]
print(len(xy_bg)/np.prod(img_input.shape[:2]))

отрисовываем штрихи

img_tmp = img_input/255
for x, y in xy_fg:
    img_tmp[x, y, :] = img_tmp[x, y, :]*0.5 + np.array([1, 0, 0]) * 0.5

for x, y in xy_bg:
    img_tmp[x, y, :] = img_tmp[x, y, :]*0.5 + np.array([0, 0, 1]) * 0.5

plt.imshow(img_tmp)

Сегментация лица на селфи без нейросетей - 8

Нечеткое разделение фона и объекта

Теперь у нас есть два набора данных: точки объекта $D_f$ и точки фона $D_b$.

points_fg = np.array([img_input[x, y, :] for (x, y) in xy_fg])
points_bg = np.array([img_input[x, y, :] for (x, y) in xy_bg])

Посмотрим на распределение цветов по RGB каналам в каждом из множеств. Первая гистограмма — для объекта, вторая — для фона.

отрисовка распределений

fig, axes = plt.subplots(nrows=2, ncols=1)
sns.distplot(points_fg[:, 0], ax=axes[0], color='r')
sns.distplot(points_fg[:, 1], ax=axes[0], color='g')
sns.distplot(points_fg[:, 2], ax=axes[0], color='b')
sns.distplot(points_bg[:, 0], ax=axes[1], color='r')
sns.distplot(points_bg[:, 1], ax=axes[1], color='g')
sns.distplot(points_bg[:, 2], ax=axes[1], color='b')

Сегментация лица на селфи без нейросетей - 11

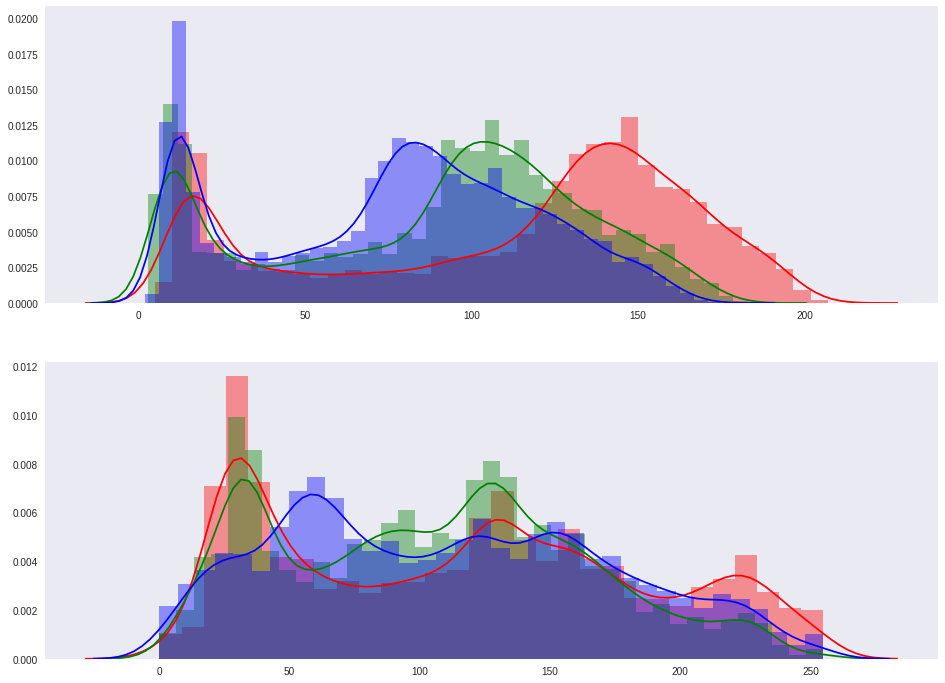
Радует, что распределения отличаются. Это значит, что если мы сможем получить функции, оценивающие вероятность принадлежности точки к нужному распределению, то мы получим нечеткие маски. И оказывается такой способ есть — kernel density estimation. Для заданного набора точек, можно построить функцию оценки плотности для новой точки $x$ следующим образом (для простоты пример для одномерного распределения):

$Fleft(xright)=frac{1}{hcdotleft|Dright|} sum_{i=1}^{left|Dright|} Kleft(frac{x - x_i}{h}right)$

где:

  • $h$ — параметр сглаживания
  • $K$ — некоторое ядро

Мы для простоты будем использовать Гауссово ядро:

$K(u)={frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}u^{2}}$

Хотя для скорости Гауссово ядро не лучший выбор и если взять ядро Епанечникова, то все будет считаться быстрее. Так же я буду использовать KernelDensity из sklearn, что в итоге выльется в 5 минут скоринга. Авторы этой статьи утверждают, что замена KDE на оптимальную реализацию сокращает расчеты на устройстве до одной секунды.

# инстанцируем классы KDE для объекта и фона
kde_fg = KernelDensity(kernel='gaussian', 
                       bandwidth=1, 
                       algorithm='kd_tree', 
                       leaf_size=100).fit(points_fg)
kde_bg = KernelDensity(kernel='gaussian', 
                       bandwidth=1, 
                       algorithm='kd_tree', 
                       leaf_size=100).fit(points_bg)

# инициализируем и вычисляем маски
score_kde_fg = np.zeros(img_input.shape[:2])
score_kde_bg = np.zeros(img_input.shape[:2])
likelihood_fg = np.zeros(img_input.shape[:2])
coodinates = it.product(range(score_kde_fg.shape[0]), 
                        range(score_kde_fg.shape[1]))
for x, y in tqdm_notebook(coodinates, 
                          total=np.prod(score_kde_fg.shape)):
    score_kde_fg[x, y] = np.exp(kde_fg.score(img_input[x, y, :].reshape(1, -1)))
    score_kde_bg[x, y] = np.exp(kde_bg.score(img_input[x, y, :].reshape(1, -1)))
    n = score_kde_fg[x, y] + score_kde_bg[x, y]
    if n == 0:
        n = 1
    likelihood_fg[x, y] = score_kde_fg[x, y]/n

В итоге у нас есть несколько масок:

  • score_kde_fg — оценка вероятности быть точкой объекта $pleft(x mid D_fright)$
  • score_kde_bg — оценка вероятности быть точкой объекта $pleft(x mid D_bright)$
  • likelihood_fg — нормализированная вероятность быть точкой объекта $p_fleft(xright)=frac{pleft(x mid D_fright)}{pleft(x mid D_fright) + pleft(x mid D_bright)}$
  • 1 - likelihood_fg нормализированная вероятность быть точкой фона $p_bleft(xright)=1 - p_fleft(xright)$

Посмотрим на следующие распределения.

Распределение значений score_kde_fg

sns.distplot(score_kde_fg.flatten())
plt.show()

Сегментация лица на селфи без нейросетей - 21

Распределение значений score_kde_bg

sns.distplot(score_kde_bg.flatten())
plt.show()

Сегментация лица на селфи без нейросетей - 22

Распределение значений likelihood_fg:

sns.distplot(likelihood_fg.flatten())
plt.show()

Сегментация лица на селфи без нейросетей - 23

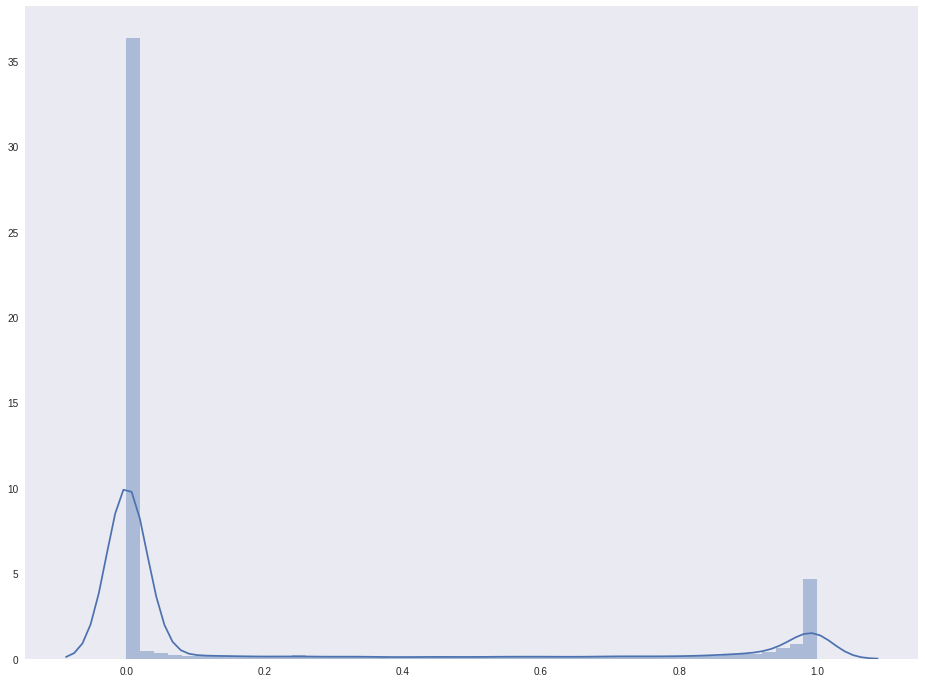
Вселяет надежду то, что на $p_fleft(xright)$ есть два пика, и количество точек, принадлежащих лицу, явно не меньше, чем фоновых точек. Нарисуем полученные маски.

маска score_kde_fg

plt.matshow(score_kde_fg, cmap=cm.bwr)
plt.show()

Сегментация лица на селфи без нейросетей - 25

маска score_kde_bg

plt.matshow(score_kde_bg, cmap=cm.bwr)
plt.show()

Сегментация лица на селфи без нейросетей - 26

plt.matshow(likelihood_fg, cmap=cm.bwr)
plt.show()

Сегментация лица на селфи без нейросетей - 27

маска 1 - likelihood_fg

plt.matshow(1 - likelihood_fg, cmap=cm.bwr)
plt.show()

Сегментация лица на селфи без нейросетей - 28

К сожалению, часть косяка двери получилась частью лица. Хорошо, что косяк далеко от лица. Этим-то свойством мы и воспользуемся в следущей части.

Бинарная маска объекта

Представим изображение как граф, узлами которого являются пиксели, а ребрами соединены точки сверху и снизу от текущей точки, а так же справа и слева от неё. Весами ребер будем считать абсолютное значение разницы вероятностей принадлежности точек к объекту или к фону:

$dleft(a, bright)=left| pleft(aright) - pleft(bright) right|$

Соответственно, чем вероятности ближе к друг другу, тем меньше вес ребра между точками. Воспользуемся алгоритмом Дейкстры для поиска наикратчайших путей и их расстояний от точки до всех остальных. Алгоритм мы вызовем два раза, подав на вход все вероятности принадлежности в объекту и затем вероятности принадлежности точек к фону. Понятие расстояния зашьем сразу в алгоритм, а расстояние между точками, принадлежащими одной группе (объекту или фону), будет равно нулю. В рамках алгоритма Дейкстры мы можем поместить все эти точки в группу посещенных вершин.

def dijkstra(start_points, w):
    d = np.zeros(w.shape) + np.infty
    v = np.zeros(w.shape, dtype=np.bool)
    q = queue.PriorityQueue()
    for x, y in start_points:
        d[x, y] = 0
        q.put((d[x, y], (x, y)))

    for x, y in it.product(range(w.shape[0]), range(w.shape[1])):
        if np.isinf(d[x, y]):
            q.put((d[x, y], (x, y)))

    while not q.empty():
        _, p = q.get()
        if v[p]:
            continue

        neighbourhood = []
        if p[0] - 1 >= 0:
            neighbourhood.append((p[0] - 1, p[1]))
        if p[0] + 1 <= w.shape[0] - 1:
            neighbourhood.append((p[0] + 1, p[1]))
        if p[1] - 1 >= 0:
            neighbourhood.append((p[0], p[1] - 1))
        if p[1] + 1 < w.shape[1]:
            neighbourhood.append((p[0], p[1] + 1))

        for x, y in neighbourhood:
            # тут вычисляется расстояние
            d_tmp = d[p] + np.abs(w[x, y] - w[p])
            if d[x, y] > d_tmp:
                d[x, y] = d_tmp
                q.put((d[x, y], (x, y)))

        v[p] = True

    return d

# вызываем алгоритм для двух масок
d_fg = dijkstra(xy_fg, likelihood_fg)
d_bg = dijkstra(xy_bg, 1 - likelihood_fg)

новая нечеткая маска объекта

plt.matshow(d_fg, cmap=cm.bwr)
plt.show()

Сегментация лица на селфи без нейросетей - 30

новая нечеткая маска фона

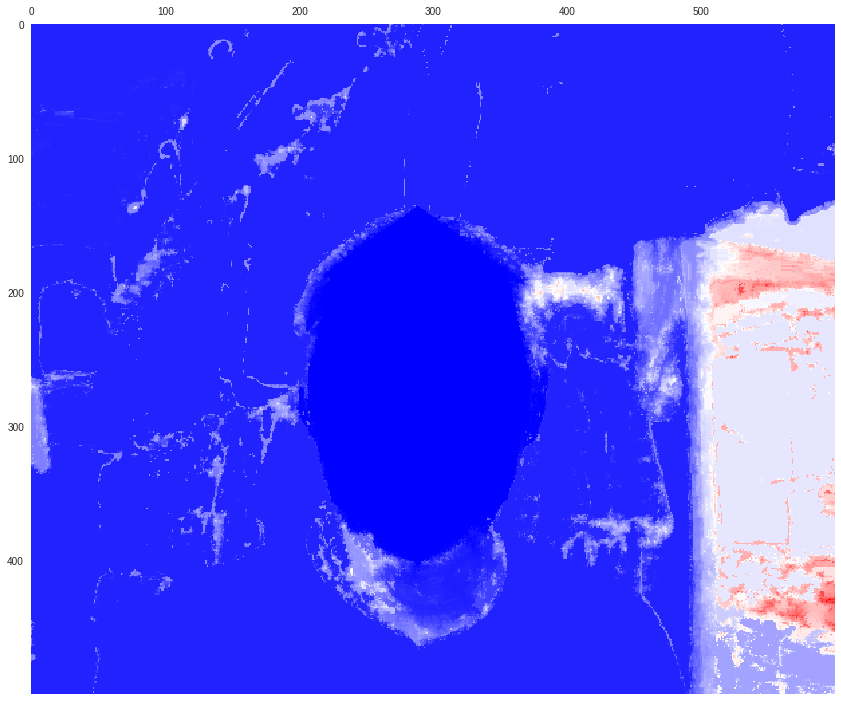
plt.matshow(d_bg, cmap=cm.bwr)
plt.show()

Сегментация лица на селфи без нейросетей - 31

А теперь относим к объекту все те точки, от которых расстояние до объекта меньше чем расстояния до фона (можно добавить некоторый зазор).

margin = 0.0
mask = (d_fg < (d_bg + margin)).astype(np.uint8)

plt.matshow(mask)
plt.show()

Сегментация лица на селфи без нейросетей - 32

Можно отправить себя в космос.

img_fg = img_input/255.0
img_bg = (np.array(Image.open('./../data/background.jpg'))/255.0)[:800, :800, :]

x = int(img_bg.shape[0] - img_fg.shape[0])
y = int(img_bg.shape[1]/2 - img_fg.shape[1]/2)

img_bg_fg = img_bg[x:(x + img_fg.shape[0]), y:(y + img_fg.shape[1]), :]
mask_3d = np.dstack([mask, mask, mask])
img_bg[x:(x + img_fg.shape[0]), y:(y + img_fg.shape[1]), :] = mask_3d*img_fg + (1 - mask_3d)*img_bg_fg

plt.imshow(img_bg)

Сегментация лица на селфи без нейросетей - 33

Сглаживание маски

Вы наверняка заметили, что маска слегка рваная на краях. Но это легко исправить методами математической морфологии.

Сегментация лица на селфи без нейросетей - 34

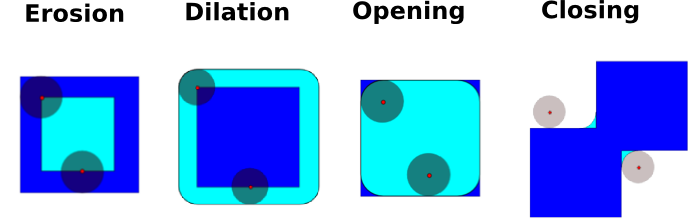
Допустим, у нас есть структурный элемент (СЭ) типа "диск" — бинарная маска диска.

  • эрозия: прикладываем к каждой точке объекта на оригинальном изображении СЭ так, чтобы совпадал центр СЭ и точка на изображении; если СЭ полностью принадлежит в объекту, то такая точка объекта остается; получается, что удаляются детали, которые меньше чем СЭ, и объект "худеет"; в примере из синего квадрата сделали голубой
  • наращивание (dilation): на каждую точку объекта накладывается СЭ, и недостающие точки дорисовываются; таким образом закрашиваются дырки меньшие чем СЭ, а объект в целом "толстеет"; на примере из синего квадрата сделали голубой, углы получились закругленные
  • размыкание (opening): сначала эрозия, потом наращивание тем же СЭ
  • замыкание (closing): сначала наращивание, потом эрозия тем же СЭ

Мы воспользуемся размыканием, что сначала удалит "волосатость" по краям, а потом вернет первоначальный размер (объект "похудеет" после эрозии).

mask = morphology.opening(mask, morphology.disk(11))
plt.imshow(mask)

Сегментация лица на селфи без нейросетей - 35

После применения такой маски результат станет поприятнее:

код применения маски

img_fg = img_input/255.0
img_bg = (np.array(Image.open('./../data/background.jpg'))/255.0)[:800, :800, :]

x = int(img_bg.shape[0] - img_fg.shape[0])
y = int(img_bg.shape[1]/2 - img_fg.shape[1]/2)

img_bg_fg = img_bg[x:(x + img_fg.shape[0]), y:(y + img_fg.shape[1]), :]
mask_3d = np.dstack([mask, mask, mask])
img_bg[x:(x + img_fg.shape[0]), y:(y + img_fg.shape[1]), :] = 
    mask_3d*img_fg + (1 - mask_3d)*img_bg_fg

plt.imshow(img_bg)

Сегментация лица на селфи без нейросетей - 36

Накладываем маску

Возьмем случайную фотку из интернетов для эксперимента по переносу лица.

Подопытный экземпляр

img_target = np.array(Image.open('./../data/target.jpg'))
img_target = (transform.rescale(img_target, scale=0.5, mode='constant')*255).astype(np.uint8)
print(img_target.shape)
plt.imshow(img_target)

Сегментация лица на селфи без нейросетей - 37

Найдем на подопытном все 62 колючевые точки лица, напомню, что они будут в том же порядке как и на любом другом лице.

img_gray = cv2.cvtColor(img_target, cv2.COLOR_BGR2GRAY)
rects_target = detector(img_gray, 0)
shape_target = predictor(img_gray, rects_target[0])
shape_target = face_utils.shape_to_np(shape_target)

Чтобы перенести одно лицо на другое, нужно первое лицо отмасштабировать под новое, повернуть и передвинуть, т.е. применить некоторое аффинное преобразование к первому лицу. Оказывается, что и аффинное преобразование не некоторое, а вполне конкретное. Оно должно быть таким, которое переводит 62 точки первого лица в 62 точки второго лица. Получается, что для получения оператора аффинного преобразования нам необходимо решить задачу линейной регрессии.

$left({begin{array}{cc} x^1_1, x^2_1, 1 \ x^1_2, x^2_2, 1 \ cdots \ x^1_{62}, x^2_{62}, 1 end{array} } right) times left({begin{array}{cc} a_1^1, a_2^1, a_3^1 \ a_1^2, a_2^2, a_3^2 \ a_1^3, a_2^3, a_3^3 \ end{array} } right)=left({begin{array}{cc} y^1_1, y^2_1, 1 \ y^1_2, y^2_2, 1 \ cdots \ y^1_{62}, y^2_{62}, 1 end{array} } right) $

Данное уравнение легко решается с помощью псевдообратной матрицы:

$large Xcdot A=Y Rightarrow A=left(X^T Xright)^{-1}X^T Y$

Так и сделаем:

# добавим справа к матрицам колонку единиц,
# иначе будет только масштабирование и поворот, без переноса
X = np.hstack((shape, np.ones(shape.shape[0])[:, np.newaxis]))
Y = np.hstack((shape_target, np.ones(shape_target.shape[0])[:, np.newaxis]))
# учим оператор
A = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)

# выбираем точки лица по искомой маске
X = np.array([(y, x, 1) for (x, y) in 
    it.product(range(mask.shape[0]), 
                   range(mask.shape[1])) if mask[x, y] == 1.0])
# вычисляем новые координаты маски на целевом изображении
Y = np.dot(X, A).astype(np.int)

Накладываем маску

img_tmp = img_target.copy()
for y, x, _ in Y:
    if x < 0 or x >= img_target.shape[0] or y < 0 or y >= img_target.shape[1]:
        continue
    img_tmp[x, y, :] = np.array([0, 0, 0])

plt.imshow(img_tmp)

Сегментация лица на селфи без нейросетей - 40

Переносим лицо

img_trans = img_target.copy().astype(np.uint8)
points_face = {}
for ix in range(X.shape[0]):
    y1, x1, _ = X[ix, :]
    y2, x2, _ = Y[ix, :]
    if x2 < 0 or x2 >= img_target.shape[0] or 
       y2 < 0 or y2 >= img_target.shape[1]:
        continue
    points_face[(x2, y2)] = img_input[x1, y1, :]

for (x, y), c in points_face.items():
    img_trans[x, y, :] = c
plt.imshow(img_trans)

Сегментация лица на селфи без нейросетей - 41

Заключение

В качестве домашней работы вы можоте самостоятельно сделать следующие улучшения:

  • добавить прозрачности по краям, чтобы был плавный переход маски в целевое изображение (matting);
  • пофиксить перенос на изображения большего размера — точек оригинального лица не хватит, чтобы покрыть все точки целевого лица, таким образом, образуются пропуски между точками; исправить это можно увеличением размера исходного лица;
  • сделать какую-либо маску, например бурундука Дейла, нанести вручную 62 точки и осуществить перенос (вот вам и маскарад);
  • использовать какой-нибудь модный нейросетевой детектор точек, который умеет искать большее количество точек.

Ноутбук с исходниками находится тут. Приятного времяпрепровождения.

Как обычно спс bauchgefuehl за редактуру.

Автор: Павел Нестеров

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js