Топология — довольно красивое, звучное слово, очень популярное в некоторых нематематических кругах, заинтересовало меня еще в 9 классе. Точного представления конечно же я не имел, тем не менее, подозревал, что все завязано на геометрии.
Слова и текст подбирались таким образом, чтобы все было «интуитивно ясно». Как следствие — полное отсутствие математической грамоты.
Что такое топология? Сразу скажу, что есть, по крайней мере, два термина «Топология» — один из них просто обозначает некоторую математическую структуру, второй — несет за собой целую науку. Наука эта заключается в изучение свойств предмета, которые не изменятся при его деформации.
Наглядный пример 1. Чашка бублик.

Мы видим, что кружка непрерывными деформациями переходит в бублик (в простонародье «двухмерный тор»). Было замечено, что топология изучает, то что остается неизменным при таких деформациях. В данном случае неизменным остается количество «дырок» в предмете — она одна. Пока оставим как есть, чуть позже разберемся наверняка)
Наглядный пример 2. Топологический человек.
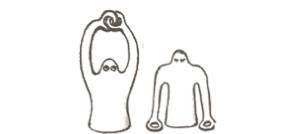
Непрерывными деформациями человек (см. рисунок) может распутать пальцы — факт. Не сразу очевидно, но можно догадаться. А если же наш топологический человек предусмотрительно одел часы на одну руку, то наша задача станет невыполнимой.
Давайте внесем ясности
И так. Надеюсь парочка примеров привнесла некоторой наглядности к происходящему.
Попробуем формализовать это все по-детски.
Будем считать что мы работаем с пластилиновыми фигурками, и пластилин можем растягивать, сжимать, при этом запрещены склеивания разных точек и разрывы. Гомеоморфными называются фигуры, которые переводятся друг в друга непрерывными деформациями описанными чуть ранее.
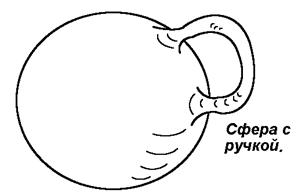
Очень полезный случай — сфера с ручками. У сферы может быть 0 ручек — тогда это просто сфера, может быть одна — тогда это бублик (в простонародье «двухмерный тор») и т.д.
Так почему же сфера с ручками — обособляется среди других фигур? Все очень просто — любая фигура гомеоморфна сфере с некоторым количеством ручек. То есть по сути у нас больше ничего нет О_о Любой объемный предмет устроен как сфера с некоторым количеством ручек. Будь то чашка, ложка, вилка (ложка=вилка!), компьютерная мышь, человек.
Вот такая вот достаточно содержательная теорема доказана. Не нами и не сейчас. Точнее она доказана для гораздо более общей ситуации. Поясню: мы ограничивались рассмотрением фигур слепленных из пластилина и без полостей. Это влечет следующие неприятности:
1) мы никак не можем получить неориентируемую поверхность (Бутылка Клейна, Лента Мёбиуса, проективная плоскость),
2)ограничиваемся двухмерными поверхностями (н/п: сфера — двухмерная поверхность),
3)не можем получить поверхности, фигуры простирающиеся на бесконечность (можно конечно такое представить, но никакого пластилина не хватит).
Лента Мёбиуса

Бутылка Клейна
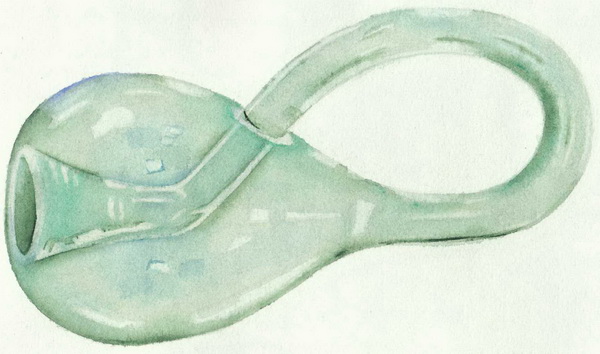
Комментарий: изображено самопересечение, что мы запрещали изначально. На самом деле если рассматривать вложение в четырехмерное пространство, то можно избавиться от самопересечений, но «БолееЧемТрехМерные» пространства — ненаглядны.
Неориентируемые поверхности примечательны тем, что они не разделяют пространство на две части, например т.к. сфера.
Но не все так плохо. А точнее, все так же хорошо как и в ориентируемом случае — любая неориентируемая двухмерная поверхность (правильно так же добавить: компактная, связная, без края) гомеоморфна сфере с некоторым количеством «пленок Мёбиуса») и ручек. К слову Бутылка Клейна — сфера с двумя пленками Мёбиуса.
Промежуточный итог
Мы ознакомились с наипростейшим изложением сути непрерывных отображений (деформаций), неявно сформулировали теорему классификации двухмерных компактных связных поверхностей без края, ознакомились на пальцах с понятием ориентируемости.
Далее будет рассказано о связи топологии с другими разделами математики/механики, постараюсь найти какие-нибудь изюминки.
Автор: puhoshville


