0x5f3759df

В этой статье мы поговорим о «магической» константе 0x5f3759df, лежащей в основе элегантного алгоритмического трюка для быстрого вычисления обратного квадратного корня.

Вот полная реализация этого алгоритма:

float FastInvSqrt(float x) {
  float xhalf = 0.5f * x;
  int i = *(int*)&x;  // представим биты float в виде целого числа
  i = 0x5f3759df - (i >> 1);  // какого черта здесь происходит ?
  x = *(float*)&i;
  x = x*(1.5f-(xhalf*x*x));
  return x;
}

Этот код вычисляет некоторое (достаточно неплохое) приближение для формулы

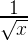
Сегодня данная реализация уже хорошо известна, и стала она такой после появления в коде игры Quake III Arena в 2005 году. Её создание когда-то приписывали Джону Кармаку, но выяснилось, что корни уходят намного дальше – к Ardent Computer, где в середине 80-ых её написал Грег Уолш. Конкретно та версия кода, которая показана выше (с забавными комментариями), действительно из кода Quake.
В этой статье мы попробуем разобраться с данным хаком, математически вывести эту самую константу и попробовать обобщить данный метод для вычисления произвольных степей от -1 до 1.

Да, понадобиться немного математики, но школьного курса будет более, чем достаточно.

Зачем?

Зачем вообще нам может понадобиться считать обратный квадратный корень, да ещё и пытаться делать это настолько быстро, что нужно реализовывать для этого специальные хаки? Потому, что это одна из основных операций в 3D программировании. При работе с 3D графикой используются нормали поверхностей. Это вектор (с тремя координатами) длиной в единицу, который нужен для описания освещения, отражения и т.д. Таких векторов нужно много. Нет, даже не просто много, а МНОГО. Как мы нормализуем (приводим длину к единице) вектор? Мы делим каждую координату на текущую длину вектора. Ну или, перефразируя, умножаем каждую координату вектора на величину:

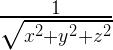
Расчёт 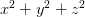относительно прост и работает быстро на всех типах процессоров. А вот расчёт квадратного корня и деление – дорогие операции. И вот поэтому – встречайте алгоритм быстрого извлечения обратного квадратного корня — FastInvSqrt.

Что он делает?

Что же делает вышеуказанная функция для вычисления результата? Она состоит из четырёх основных шагов. Первым делом она берёт входное число (которое пришло нам в формате float) и интерпретирует его биты как значение новой переменной i типа integer (целое число).

int i = *(int*)&x;         // представим биты float в виде целого числа

Далее над полученным целым числом выполняется некоторая целочисленная арифметическая операция, которая работает достаточно быстро и даёт нам некоторую аппроксимацию требуемого результата

i = 0x5f3759df - (i >> 1);  // какого черта здесь происходит ?

То, что мы получили в результате данной операции, ещё не является, собственно, результатом. Это лишь целое число, биты которого представляют некоторое другое число с плавающей запятой, которое нам нужно. А значит, необходимо выполнить обратное преобразование int во float.

x = *(float*)&i;

И, наконец, выполняется одна итерация метода Ньютона для улучшения аппроксимации.

x = x*(1.5f-(xhalf*x*x));

И вот теперь у нас имеется отличная аппроксимация операции извлечения обратного квадратного корня. Последняя часть алгоритма (метод Ньютона) – достаточно тривиальная вещь, я не буду на этом останавливаться. Ключевой частью алгоритма является шаг №2: выполнение некоторой хитрой арифметической операции над целым числом, полученным от интерпретации битов числа с плавающей запятой в качестве содержимого типа int. На этом мы и сфокусируемся.

Какого черта здесь происходит?

Для понимания дальнейшего текста нам нужно вспомнить формат, в котором хранятся в памяти числа с плавающей запятой. Я опишу здесь только то, что важно здесь для нас (остальное всегда можно подсмотреть в Википедии). Число с плавающей запятой хранится как комбинация трёх составляющих: знака, экспоненты и мантиссы. Вот биты 32-битного числа с плавающей запятой:

Первым идёт бит знака, дальше 8 битов экспоненты и 23 бита мантиссы. Поскольку мы здесь имеем дело с вычислением квадратного корня, то я предположу, что мы будем иметь дело лишь с положительными числами (первый бит всегда будет 0).
Рассматривая число с плавающей запятой как просто набор битов, экспонента и мантисса могут восприниматься как просто два положительных целых числа. Давайте обозначим их, соответственно, Е и М (поскольку дальше мы будем часто на них ссылаться). С другой стороны, интерпретируя биты числа с плавающей запятой, мы будем рассматривать мантиссу как число между 0 и 1, т.е. все нули в мантиссе будут означать 0, а все единицы – некоторое число очень близкое (но всё же не равное) 1. Ну и вместо того, чтобы интерпретировать экспоненту как беззнаковое 8-битное целое число, давайте вычтем смещение (обозначим его как В), чтобы получить знаковое целое число в диапазоне от -127 до 128. Давайте обозначим float-интерпретацию этих значений как е и m. Чтобы не путаться, будем использовать прописные обозначения (Е, М) для обозначения целочисленных значений и строчные (е, m) – для обозначения чисел с плавающей запятой (float).

Преобразование из одного в другое тривиально:

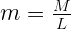
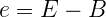
В этих формулах для 32-битных чисел L = 2^23, а В = 127. Имея некоторые значения e и m, можно получить само представляемое ими число:

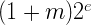
и значение соответствующей им целочисленной интерпретации числа:

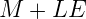
Теперь у нас есть почти все кусочки паззла, которые нужны для объяснения “хака” в коде выше. Итак, нам на вход приходит некоторое число х и требуется рассчитать его обратный квадратный корень:

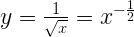
По некоторым причинам, которые вскоре станут понятны, я начну с того, что возьму логарифм по основанию 2 от обеих частей данного уравнения:

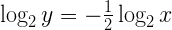
Поскольку числа, с которыми мы работаем, на самом деле являются числами с плавающей запятой, мы можем представить х и у согласно вышеуказанной формуле представления таких чисел:

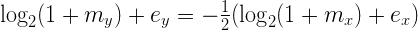
Ох уж эти логарифмы. Возможно, вы не пользовались ими со школьных времён и немного подзабыли. Не волнуйтесь, немного дальше мы избавимся от них, но пока что они нам ещё нужны, так что давайте посмотрим, как они здесь работают.
В обеих частях уравнения у нас находится выражение вида:

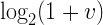
где v находится в диапазоне от 0 до 1. Можно заметить, что для v от 0 до 1 эта функция достаточно близка к прямой линии:

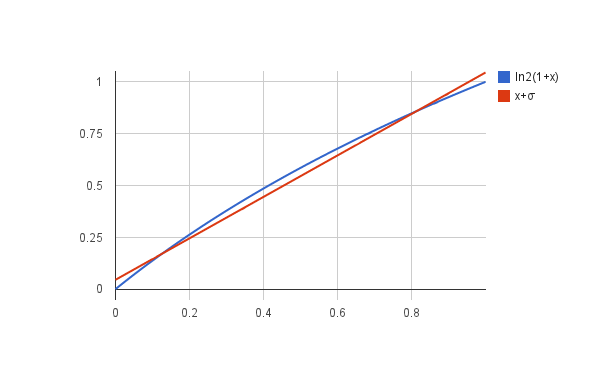
Ну или в виде выражения:

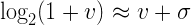
Где σ – некоторая константа. Это не идеальное приближение, но мы можем попытаться подобрать σ таким образом, чтобы оно было достаточно неплохим. Теперь, использовав его, мы можем преобразовать вышеуказанное равенство с логарифмами в другое, уже не строго равное, но достаточно близкое и, самое главное, СТРОГО ЛИНЕЙНОЕ выражение:

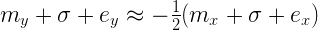
Это уже что-то! Теперь самое время прекратить работать с представлениями в виде чисел с плавающей запятой и перейти к целочисленному представлению мантиссы и экспоненты:

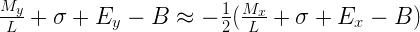
Выполнив ещё несколько тривиальных преобразований (можно пропустить детали), мы получим нечто, выглядящее уже довольно знакомо:

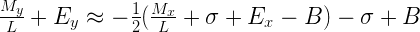
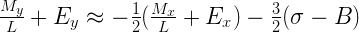
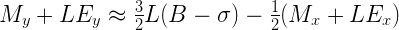
Посмотрите внимательно на левую и правую части последнего уравнения. Как мы видим, у нас получилось выражение целочисленной формы требуемого значения y, выраженное через линейного вида формулу, включающую целочисленное представление значения х:

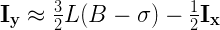
Говоря простыми словами: “y (в целочисленной форме) – это некоторая константа минус половина от целочисленной формы х”. В виде кода это:

i = K - (i >> 1);

Очень похоже на формулу в коде функции в начале статьи, правда?

Нам осталось найти константу K. Мы уже знаем значения B и L, но ещё не знаем чему равно σ.
Как вы помните, σ – это некоторое “поправочное значение”, которое мы ввели для улучшения аппроксимации функции логарифма к прямой линии на отрезке от 0 до 1. Т.е. мы можем подобрать это число сами. Я возьму число 0.0450465, как дающее неплохое приближение и использованное в оригинальной реализации. Используя его, мы получим:

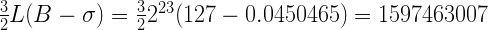
Угадаете, как число 1597463007 представляется в HEX? Ну, конечно, это 0x5f3759df. Ну, так и должно было получиться, поскольку я выбрал σ таким образом, чтобы получить именно это число.

Таким образом, данное число не является битовой маской (как думают некоторые люди просто потому, что оно записано в hex-форме), а результатом вычисления аппроксимации.

Но, как сказал бы Кнут: “Мы пока что лишь доказали, что это должно работать, но не проверили, что это действительно работает”. Чтобы оценить качество нашей формулы, давайте нарисуем графики вычисленного таким образом значения обратного квадратного корня и настоящей, точной его реализации:

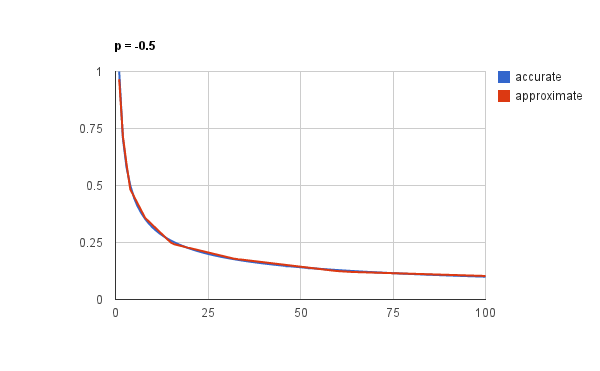
График построен для чисел от 1 до 100. Неплохо, правда? И это никакая не магия, не фокус, а просто правильное использование несколько, возможно, экзотичного трюка с представлением чисел с плавающей запятой в виде целочисленных и наоборот.

Но и это ещё не всё!

Все вышеуказанные преобразования и выражения дали нам не только объяснение константы 0x5f3759df, но и ещё несколько ценных выводов.
Во-первых, поговорим о значениях чисел L и B. Они определяются не нашей задачей по извлечению обратного квадратного корня, а форматом хранения числа с плавающей запятой. Это означает, что тот же трюк может быть проделан и для 64-битных и для 128-битных чисел с плавающей запятой – нужно лишь повторить вычисления для рассчета других констант.
Во-вторых, нам не очень-то и важно выбранное значение σ. Оно может не давать (да и на самом деле – не даёт) лучшую аппроксимацию функции x + σ к логарифму. σ выбрано таким, поскольку оно даёт лучший результат совместно с последующим применением алгоритма Ньютона. Если бы мы его не применяли, то выбор σ являлся бы отдельной интересной задачей сам по себе, эта тема раскрыта в других публикациях.

Ну и в конце-концов, давайте посмотрим на коэффициент “-1/2” в финальной формуле. Он получился таким из-за сути того, что мы хотели вычислить (“обратного квадратного корня”). Но, в общем, степень здесь может быть любой от -1 до 1. Если мы обозначим степень как р и обобщим все те же самые преобразования, то вместо “-1/2” мы получим:

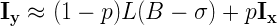
Давайте положим р=0.5 Это будет вычисление обычного (не обратного) квадратного корня числа:

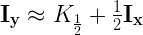
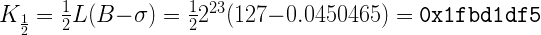
В виде кода это будет:

i = 0x1fbd1df5 + (i >> 1);

И что, это работает? Конечно, работает:

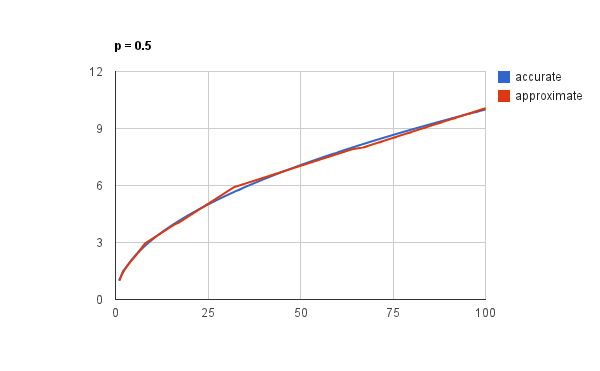
Это, наверное, хорошо известный способ быстрой аппроксимации значения квадратного корня, но беглый гуглинг не дал мне его названия. Возможно, вы подскажете?
Данный способ будет работать и с более “странными” степенями, вроде кубического корня:

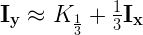
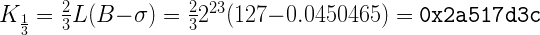
Что в коде будет выражено, как:

i = (int) (0x2a517d3c + (0.333f * i));

К сожалению, из-за степени 1/3 мы не можем использовать битовые операции сдвига и вынуждены применить здесь умножение на 0.333f. Аппроксимация всё ещё достаточно хороша:

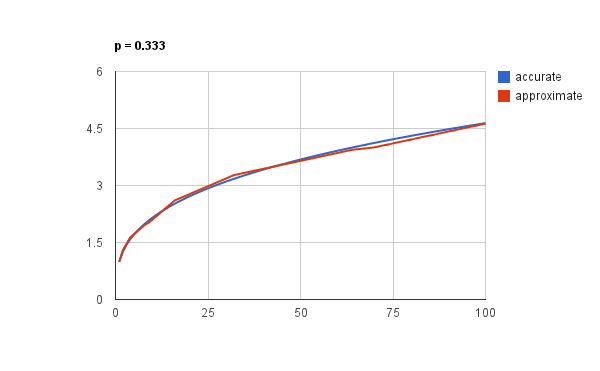
И даже более того!

К этому моменту вы уже могли заменить, что изменение степени вычисляемой функции достаточно тривиально меняет наши вычисления: мы просто рассчитываем новую константу. Это совершенно не затратная операция и мы вполне можем делать это даже на этапе выполнения кода, для разных требуемых степеней. Если мы перемножим две заранее известных константы:

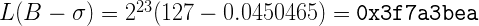
То сможем вычислять требуемые значения на лету, для произвольной степени от -1 до 1:

i = (1 - p) * 0x3f7a3bea + (p * i);

Чуть упростив выражение, мы даже можем сэкономить на одном умножении:

i = 0x3f7a3bea + p * (i - 0x3f7a3bea);

Эта формула даёт нам “магическую” константу, с помощью которой можно рассчитывать на лету разные степени чисел (для степеней от -1 до 1). Для полного счастья нам не хватает лишь уверенности в том, что вычисленное таким образом приближенное значение может быть столь же эффективно улучшено алгоритмом Ньютона, как это происходило в оригинальной реализации для обратного квадратного корня. Я не изучал эту тему более глубоко и это, вероятно, будет темой отдельной публикации (наверное, не моей).

Выражение выше содержит новую “магическую константу” 0x3f7a3bea. В некотором смысле (из-за своей универсальности) она даже “более магическая”, чем константа в оригинальном коде. Давайте назовём её С и посмотрим на неё чуть внимательнее.

Давайте проверим работу нашей формулы для случая, когда p = 0. Как вы помните из курса математики, любое число в степени 0 равно единице. Что же будет с нашей формулой? Всё очень просто – умножение на 0 уничтожит второе слагаемое и у нас останется:

i = 0x3f7a3bea;

Что, действительно является константой и, будучи переведённой во float-формат, даст нам 0.977477 – т.е. “почти 1”. Поскольку мы имеем дело с аппроксимациями – это неплохое приближение. Кроме того, это говорит нам кое-что ещё. Наша константа С имеет совершенно не случайное значение. Это единица в формате чисел с плавающей запятой (ну или “почти единица”)
Это интересно. Давайте взглянем поближе:

Целочисленное представление C это:

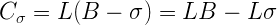
Это почти, но всё же не совсем, форма числа с плавающей запятой. Единственная проблема – мы вычитаем вторую часть выражения, а должны были бы её прибавлять. Но это можно исправить:

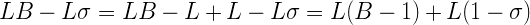
Вот теперь это выглядит в точности как целочисленное представление числа с плавающей запятой. Чтобы определить, какого именно числа, мы вычислим экспоненту и мантиссу, а потом уже и само число С. Вот экспонента:

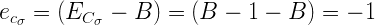
А вот мантисса:

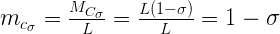
А, значит, значение самого числа будет равно:

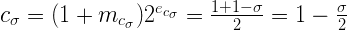
И правда, если поделить наше σ (а оно было равно 0.0450465) на 2 и отнять результат от единицы, то мы получим уже известное нам 0.97747675, то самое, которое “почти 1”. Это позволяет нам посмотреть на С с другой стороны и вычислять его на рантайме:

float sigma = 0.0450465;
float c_sigma = 1 - (0.5f * sigma);
int C_sigma = *(*int)&c_sigma;

Учтите, что для фиксированного σ все эти числа будут константами и компилятор сможет рассчитать их на этапе компиляции. Результатом будет 0x3f7a3beb, что не совсем 0x3f7a3bea из расчетов выше, но отличается от него всего на 1 бит (наименее значимый). Получить из этого числа оригинальную константу из кода (и заголовка данной статьи) можно, умножив результат вычислений ещё на 1.5.

Со всеми этими выкладками мы приблизились к пониманию того, что в коде в начале статьи нет никакой “магии”, “фокусов”, “интуиции”, “подбора” и прочих грязных хаков, а есть лишь чистая математика, во всей своей первозданной красоте. Для меня главным выводом из этой истории стала новость о том, что преобразование float в int и наоборот путем переинтерпретации одного и того же набора бит – это не ошибка программиста и не “хак”, а вполне себе иногда разумная операция. Слегка, конечно, экзотическая, но зато очень быстрая и дающая практически полезные результаты. И, мне кажется, для этой операции могут быть найдены и другие применения – будем ждать.

Автор: Владимир

Источник