В этой статье будет продемонстрирована техника обработки информации по биржевым котировкам с помощью пакета pandas (python), а также изучены некоторые «мифы и легенды» биржевой торговли посредством применения методов математической статистики. Попутно кратко рассмотрим особенности использования библиотеки plotly.
Одной из легенд трейдеров является понятие «локомотива». Описать ее можно следующим образом: есть бумаги «ведущие» и есть бумаги «ведомые». Если поверить в существование подобной закономерности, то можно «предсказывать» будущие движения финансового инструмента по движению «локомотивов» («ведущих» бумаг). Так ли это? Есть ли под этим основания?
Сформулируем задачу. Есть финансовые инструменты: A, B, C, D; есть характеристика времени — t. Существуют ли связи между движениями этих инструментов:
At и Bt-1; At и Ct-1; At и Dt-1
Вt и Сt-1; Bt и Dt-1; Bt и At-1
Ct и Dt-1; Ct и At-1; Ct и Bt-1
Dt и At-1; Dt и Bt-1; Dt и Bt-1
Как получить данные для исследования этого вопроса? Насколько сильны, стабильны упомянутые связи? Как их можно измерить? Какими инструментами?
Предварительно заметим, что на сегодняшний день существует значительное количество прогнозных моделей. В некоторых источниках говорится о том, что их число превысило отметку ста. К слову — основная шутка действительности в том, что … чем сложнее модель, тем труднее интерпретация, понимание каждой отдельной компоненты этой самой модели. Подчеркну, что цель данной статьи – ответить на поставленные выше вопросы, а не использовать одну из существующих моделей прогнозирования.
Пакет pandas является мощным средством для анализа данных, который имеет богатый арсенал инструментов. Используем его возможности, чтобы изучить поставленные нами вопросы.
Предварительно, получим котировки с сервера компании «ФИНАМ». Будем брать «часовики» за период с 01.01.2017 по 13.07.2017. Немного модифицировав функцию, упомянутую здесь, получим:
# -*- coding: utf-8 -*-
"""
@author: optimusqp
"""
import os
import urllib
import pandas as pd
import time
import codecs
from datetime import datetime, date
from pandas.io.common import EmptyDataError
e='.csv';
p='7';
yf='2017';
yt='2017';
month_start='01';
day_start='01';
month_end='07';
day_end='13';
year_start=yf[2:];
year_end=yt[2:];
mf=(int(month_start.replace('0','')))-1;
mt=(int(month_end.replace('0','')))-1;
df=(int(day_start.replace('0','')));
dt=(int(day_end.replace('0','')));
dtf='1';
tmf='1';
MSOR='1';
mstimever='0'
sep='1';
sep2='1';
datf='5';
at='1';
def quotes_finam_optimusqp(data,year_start,month_start,day_start,year_end,month_end,day_end,e,df,mf,yf,dt,mt,yt,p,dtf,tmf,MSOR,mstimever,sep,sep2,datf,at):
temp_name_file='id,companyn';
incrim=1;
for index, row in data.iterrows():
page = urllib.urlopen('http://export.finam.ru/'+str(row['code'])+'_'+str(year_start)+str(month_start)+str(day_start)+'_'+str(year_end)+str(month_end)+str(day_end)+str(e)+'?market='+str(row['id_exchange_2'])+'&em='+str(row['em'])+'&code='+str(row['code'])+'&apply=0&df='+str(df)+'&mf='+str(mf)+'&yf='+str(yf)+'&from='+str(day_start)+'.'+str(month_start)+'.'+str(yf)+'&dt='+str(dt)+'&mt='+str(mt)+'&yt='+str(yt)+'&to='+str(day_end)+'.'+str(month_end)+'.'+str(yt)+'&p='+str(p)+'&f='+str(row['code'])+'_'+str(year_start)+str(month_start)+str(day_start)+'_'+str(year_end)+str(month_end)+str(day_end)+'&e='+str(e)+'&cn='+str(row['code'])+'&dtf='+str(dtf)+'&tmf='+str(tmf)+'&MSOR='+str(MSOR)+'&mstimever='+str(mstimever)+'&sep='+str(sep)+'&sep2='+str(sep2)+'&datf='+str(datf)+'&at='+str(at))
print('http://export.finam.ru/'+str(row['code'])+'_'+str(year_start)+str(month_start)+str(day_start)+'_'+str(year_end)+str(month_end)+str(day_end)+str(e)+'?market='+str(row['id_exchange_2'])+'&em='+str(row['em'])+'&code='+str(row['code'])+'&apply=0&df='+str(df)+'&mf='+str(mf)+'&yf='+str(yf)+'&from='+str(day_start)+'.'+str(month_start)+'.'+str(yf)+'&dt='+str(dt)+'&mt='+str(mt)+'&yt='+str(yt)+'&to='+str(day_end)+'.'+str(month_end)+'.'+str(yt)+'&p='+str(p)+'&f='+str(row['code'])+'_'+str(year_start)+str(month_start)+str(day_start)+'_'+str(year_end)+str(month_end)+str(day_end)+'&e='+str(e)+'&cn='+str(row['code'])+'&dtf='+str(dtf)+'&tmf='+str(tmf)+'&MSOR='+str(MSOR)+'&mstimever='+str(mstimever)+'&sep='+str(sep)+'&sep2='+str(sep2)+'&datf='+str(datf)+'&at='+str(at))
print('code: '+str(row['code']))
#Формируем перечень файлов в которых будут содержаться котировки.
#Один файл - один торгуемый инструмент
file = codecs.open(str(row['code'])+"_"+"0"+".csv", "w", "utf-8")
content = page.read()
file.write(content)
file.close()
temp_name_file = temp_name_file + (str(incrim) + "," + str(row['code'])+"n")
incrim+=1
time.sleep(2)
#Формируем файл в котором содержатся code заголовки торгуемых инструментов,
#из расчета одна строка - один заголовок.
write_file = "name_file_data.csv"
with open(write_file, "w") as output:
for line in temp_name_file:
output.write(line)
#Перед запуском quotes_finam_optimusqp в распоряжении должен быть
#файл параметров function_parameters.csv
#___http://optimusqp.ru/articles/articles_1/function_parameters.csv
data_all = pd.read_csv('function_parameters.csv', index_col='id')
#Сузим область нашей выборки до тех инструментов, которые торгуются
#исключительно на id_exchange_2 == 1, т.е. МосБиржа акции
data = data_all[data_all['id_exchange_2']==1]
quotes_finam_optimusqp(data,year_start,month_start,day_start,year_end,month_end,day_end,e,df,mf,yf,dt,mt,yt,p,dtf,tmf,MSOR,mstimever,sep,sep2,datf,at)
В результате имеем перечень файлов типа A_0.csv:
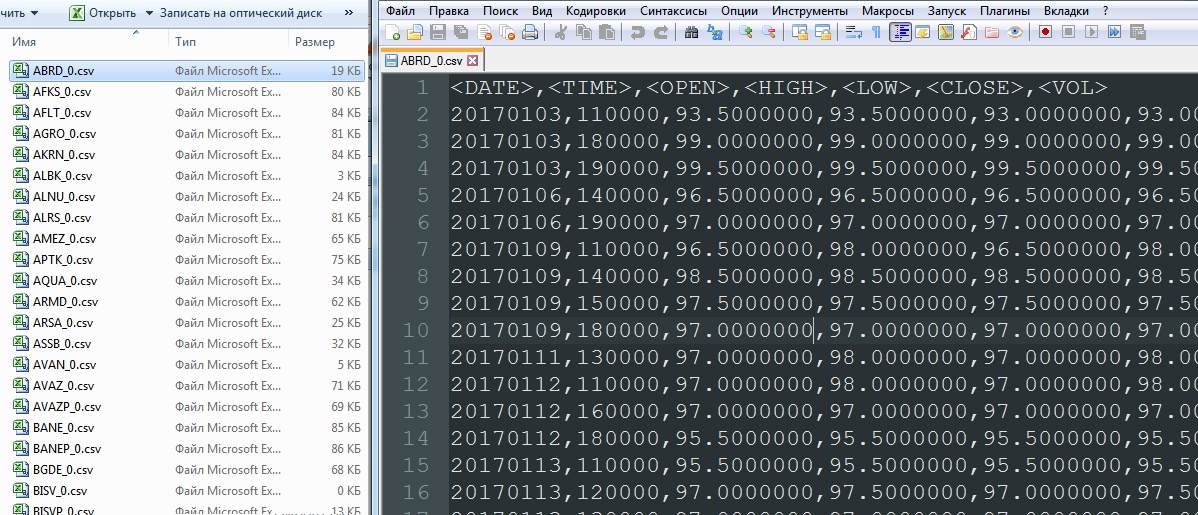
Далее определяем движения финансовых инструментов At-At-1, удаляем столбцы OPEN, HIGH, LOW, VOL, формируем единый столбец DATETIME. Произведем отсев тех финансовых инструментов, которые имеют слишком мало данных для анализа (торгуются недавно, нестабильно либо обладают малой ликвидностью).
#Зачем мы записываем файлы, и потом их считываем тут же?
#Все просто - ради наглядности процесса.
name_file_data = pd.read_csv('name_file_data.csv', index_col='id')
incrim=1;
#Введем показатель how_work_days - он нужен нам затем, чтобы не рассматривать
#неликвидные инструменты, либо инструменты с малой продолжительностью торговли
#на рынке
temp_string_in_file='id,how_work_daysn';
for index, row1 in name_file_data.iterrows():
how_string_in_file = 0
#открываем файл с котировкой по инструменту, в соответствие с имеющейся маской
name_file=row1['company']+"_"+"0"+".csv"
#а существует ли файл котировок? проверка файла на существование
if os.path.exists(name_file):
folder_size = os.path.getsize(name_file)
#если файл котировок имеет нулевой вес - следовательно он пуст, и мы можем его просто удалить
if folder_size>0:
temp_quotes_data=pd.read_csv(name_file, delimiter=',')
#если файл котировок пуст, в соответствие с исключением типа EmptyDataError
#его также удаляем
try:
#здесь будем рассматривать цены закрытия (CLOSE);
#остальные столбцы можем просто удалить
quotes_data = temp_quotes_data.drop(['<OPEN>', '<HIGH>', '<LOW>', '<VOL>'], axis=1)
#Определяем - какое количество строк в файле котировок
how_string_in_file = len(quotes_data.index)
#если файл котировок имеет количество строк менее чем 1 100,
#удаляем его; причина отсев неликвидных инструментов
if how_string_in_file>1100:
#формируем построчные записи для файла days_data.csv, в котором
#определяется количество периодов в течение которых торговался
#данный инструмент
temp_string_in_file = temp_string_in_file + (str(incrim) + "," + str(how_string_in_file)+"n")
incrim+=1
quotes_data['DATE_str']=quotes_data['<DATE>'].astype(basestring)
quotes_data['TIME_str']=quotes_data['<TIME>'].astype(basestring)
#"сливаем" дату и время в единый показатель DATETIME
quotes_data['DATETIME'] = quotes_data.apply(lambda x:'%s%s' % (x['DATE_str'],x['TIME_str']),axis=1)
quotes_data = quotes_data.drop(['<DATE>','<TIME>','DATE_str','TIME_str'], axis=1)
quotes_data['DATETIME'].apply(lambda d: datetime.strptime(d, '%Y%m%d%H%M%S'))
quotes_data [row1['company']] = quotes_data['<CLOSE>'] - quotes_data['<CLOSE>'].shift(1)
quotes_data = quotes_data.drop(['<CLOSE>'], axis=1)
quotes_data.to_csv(row1['company']+"_"+"1"+".csv", sep=',', encoding='utf-8')
os.unlink(row1['company']+"_"+"0"+".csv")
else:
os.unlink(row1['company']+"_"+"0"+".csv")
except pd.io.common.EmptyDataError:
os.unlink(row1['company']+"_"+"0"+".csv")
else:
os.unlink(row1['company']+"_"+"0"+".csv")
else:
continue
write_file = "days_data.csv"
with open(write_file, "w") as output:
for line in temp_string_in_file:
output.write(line)
В результате получим перечень файлов типа A_1.csv. Всего 91 файл:
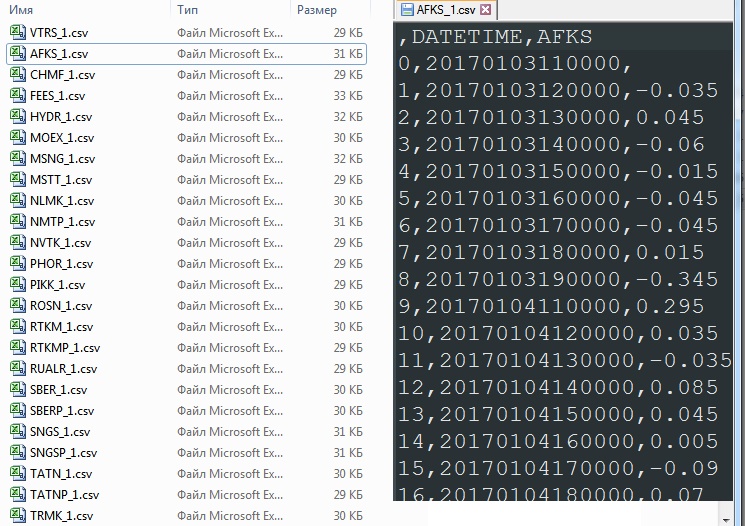
«Сливаем» в один файл securities.csv все движения всех финансовых инструментов, удалив первую пустую строку.
import glob
allFiles = glob.glob("*_1.csv")
frame = pd.DataFrame()
list_ = []
for file_ in allFiles:
df = pd.read_csv(file_,index_col=None, header=0)
list_.append(df)
dfff = reduce(lambda df1,df2: pd.merge(df1,df2,on='DATETIME'), list_)
quotes_data = dfff.drop(['Unnamed: 0_x', 'Unnamed: 0_y', 'Unnamed: 0'], axis=1)
quotes_data.to_csv("securities.csv", sep=',', encoding='utf-8')
quotes_data = quotes_data.drop(['DATETIME'], axis=1)
number_columns=len(quotes_data.columns)
columns_name_0 = quotes_data.columns
columns_name_1 = quotes_data.columns
На данном этапе происходит довольно интересная операция объединения записей по столбцу DATETIME (pd.merge). Этот порядок объединения отбрасывает те даты, в которые не торговалась хотя бы одна из 91 ценной бумаги. То есть объединение основано на полном исключении пустых данных. В результате:
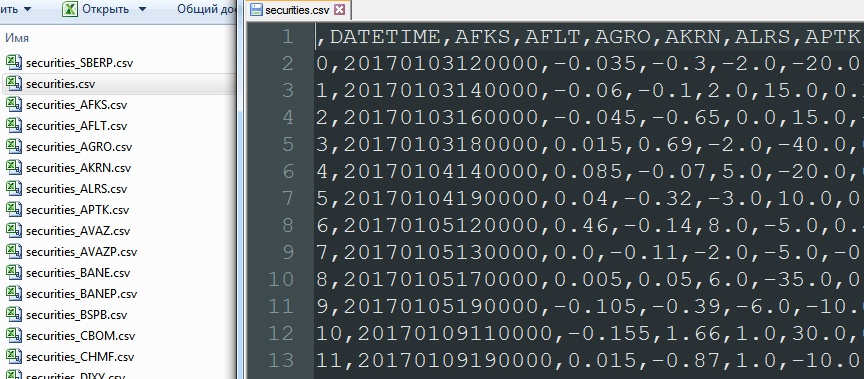
В файле securities.csv, оперируя данными в цикле сдвигаем все строки, кроме текущей. Таким образом, напротив At оказываются значения Bt-1, Ct-1, Dt-1.
incrim=0
quotes_data_w=quotes_data.shift(1)
for column in columns_name_0:
quotes_data_w[column]=quotes_data_w[column].shift(-1)
quotes_data_w.to_csv("securities_"+column+".csv", sep=',', encoding='utf-8')
#Вернем на место сдвинутые строки
quotes_data_w[column]=quotes_data_w[column].shift(1)
incrim+=1
Данные будут выглядеть так:
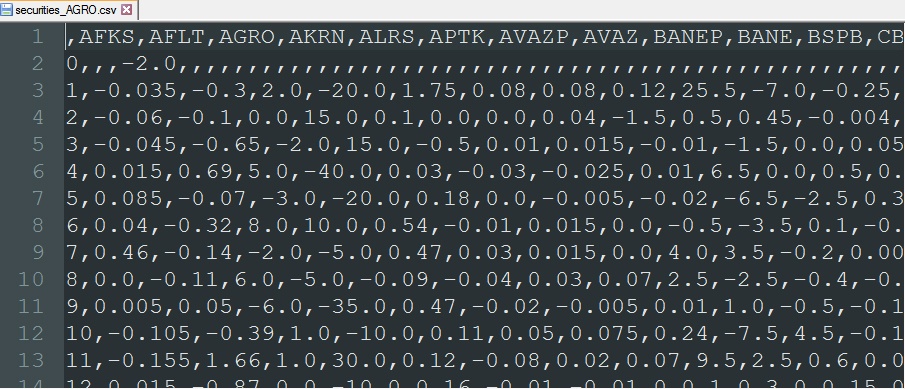
И, да, необходимо удалить первую строку с пустыми данными. Теперь можно построить корреляции между столбцами. Они то и выявят существование либо отсутствие бумаг-«локомотивов»… или дадут возможность уверится, что «локомотивы» — это не более чем миф.
О факте отсутствия нормального (Гаусса) распределения в движении финансовых инструментов говорится относительно недавно. Тем не менее, большинство финансовых моделей строится как раз таки на его допущении. А присутствует ли распределение Гаусса в наших данных? Вопрос не является праздным, поскольку существование нормальности позволит использовать корреляцию Пирсона, а отсутствие обяжет использовать непараметрический вид корреляции. С этим вопросом обратимся к замечательному сервису plotly.
Чем интересен данный сервис? Во-первых, возможностью графической интерпретации данных. Во-вторых, набором статистических методов-тестов; в частности, возможностью проведения тестов на соответствие выборки нормальному (Гаусса) распределению. Будем использовать следующие тесты: критерий Шапиро-Уилка (Shapiro-Wilk), критерий Колмогорова-Смирнова (Kolmogorov-Smirnov) см. правила работы здесь .
Сервис, связанный с plotly, достоин самых высоких похвал. Тутор по настройке работы plotly на Linux можно посмотреть, на plot.ly, а под Windows, например, здесь. Но на plotly есть и странности. И вопрос здесь не много ни мало в описании логики работы теста. В примерах к применению дается таблица:
Разработчик дает следующий комментарий:
Since our p-value is much less than our Test Statistic, we have good evidence to not reject the null hypothesis at the 0.05 significance level.
Перевод:
Поскольку наше значение p намного меньше, чем наша тестовая статистика, у нас есть хорошие доказательства того, что мы не отказываемся от нулевой гипотезы на уровне значимости 0,05.
Таким образом, согласно данной рекомендации мы не вправе отказаться от гипотезы о нормальности распределения по рассматриваемой выборке! Но… данный совет не является верным.
Итак, вспомним — что же такое p-value? Эта величина необходима для проведения тестирования статистических гипотез. Ее можно понимать как вероятность ошибки если мы отклоним нулевую гипотезу. Под нулевой гипотезой в критерии Шапиро-Уилка H0, напомню, имеется ввиду то, что «случайная величина X распределена нормально». Если мы отклоним H0 при чрезвычайно малом значении p-value (близком к нулю), то мы не ошибемся. Не ошибемся, исключив предположение о нормальности распределения. Вообще уровень значимости в тестах plotly на нормальность составляет 0.05 и принятие либо не принятие нулевой гипотезы должно основываться на сопоставлении данного значения p-значению. Превышение порога уровня значимости величиной p-value говорит о том, что нельзя отклонять гипотезу о нормальности распределения тестируемой выборки.
А… вдруг и… сами тесты на нормальность распределения на plotly не корректны? Забегая вперед скажу — все в порядке. Мною были сгенерирированы два вида рандомных выборок – гауссовская и парето; эти массивы данных последовательно отправляем на plot.ly. Тестируем. Характер распределений, сильно отличается и очевидно, что Парето выборки не должны пройти тест на «нормальность».
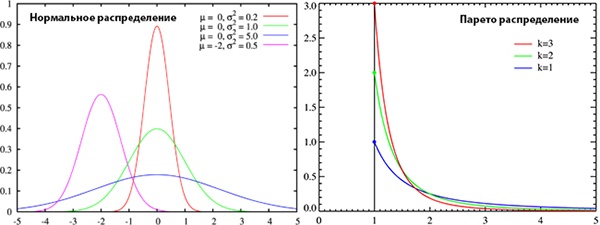
Код тестов:
import pandas as pd
import matplotlib.pyplot as plt
import plotly.plotly as py
import plotly.graph_objs as go
from plotly.tools import FigureFactory as FF
import numpy as np
from scipy import stats, optimize, interpolate
def Normality_Test(L):
x = L
shapiro_results = scipy.stats.shapiro(x)
matrix_sw = [
['', 'DF', 'Test Statistic', 'p-value'],
['Sample Data', len(x) - 1, shapiro_results[0], shapiro_results[1]]
]
shapiro_table = FF.create_table(matrix_sw, index=True)
py.iplot(shapiro_table, filename='pareto_file')
#py.iplot(shapiro_table, filename='normal_file')
#L =np.random.normal(115.0, 10, 860)
L =np.random.pareto(3,50)
Normality_Test(L)
Результаты обработки можно посмотреть в своем профайле на plot.ly/organize/home
Итак, вот некоторые результаты тестов Шапиро-Уилка:
Для Парето распределения
Первый тест
Второй тест
Для нормального (Гаусса) распределения
Первый тест
Второй тест
Итак, алгоритм теста работает корректно. Однако советы по использованию теста не совсем, мягко говоря, верны. Мораль в следующем: будьте бдительны! Возле правильно написанного инструмента не всегда лежит правильно написанная инструкция!
Перейдем к тестированию движения финансовых инструментов на нормальность (Гаусса) распределения с применением библиотеки plotly. Мною были получены следующие результаты:
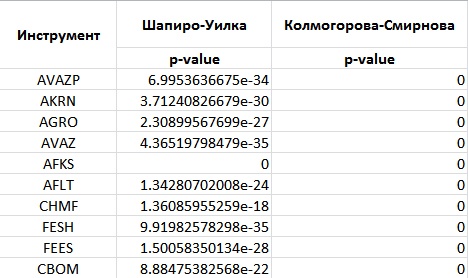
По остальным финансовым инструментам схожая картина. Следовательно – исключаем предположение о нормальности распределения в движении рассматриваемых финансовых инструментов. Код самого теста:
allFiles = glob.glob("*_1.csv")
def Shapiro(df,temp_header):
df=df.drop(df.index[0])
x = df[temp_header].tolist()
shapiro_results = scipy.stats.shapiro(x)
matrix_sw = [
['', 'DF', 'Test Statistic', 'p-value'],
['Sample Data', len(x) - 1, shapiro_results[0], shapiro_results[1]]
]
shapiro_table = FF.create_table(matrix_sw, index=True)
py.iplot(shapiro_table, filename='shapiro-table_'+temp_header)
def Kolmogorov_Smirnov(df,temp_header):
df=df.drop(df.index[0])
x = df[temp_header].tolist()
ks_results = scipy.stats.kstest(x, cdf='norm')
matrix_ks = [
['', 'DF', 'Test Statistic', 'p-value'],
['Sample Data', len(x) - 1, ks_results[0], ks_results[1]]
]
ks_table = FF.create_table(matrix_ks, index=True)
py.iplot(ks_table, filename='ks-table_'+temp_header)
frame = pd.DataFrame()
list_ = []
for file_ in allFiles:
df = pd.read_csv(file_,index_col=None, header=0)
print(file_)
columns = df.columns
temp_header = columns[2]
Shapiro(df,temp_header)
time.sleep(3)
Kolmogorov_Smirnov(df,temp_header)
time.sleep(3)
Поскольку мы не можем полагаться на нормальность (Гаусса) распределения – следовательно, при расчете корреляций необходимо выбрать непараметрический инструмент, а именно корреляцию Спирмена (Spearman rank correlation coefficient). После того как определились с видом корреляции можно перейти непосредственно к ее расчетам:
incrim=0
for column0 in columns_name_1:
df000 = pd.read_csv('securities_'+column0+".csv",index_col=None, header=0)
#Удаляем первую строку с пустотами
df000=df000.drop(df000.index[0])
df000 = df000.drop(['Unnamed: 0'], axis=1)
#Поочередно рассчитываем корреляцию Спирмена для каждого
#инструмента по отношению к прошлым периодам других ценных бумаг
corr_spr=df000.corr('spearman')
#Отсортируем строки в полученном файле корреляций от
#больших значений к меньшим
corr_spr=corr_spr.sort_values([column0], ascending=False)
#Сохраняем как отдельный DataFrame
corr_spr_temp=corr_spr[column0]
corr_spr_temp.to_csv("corr_"+column0+".csv", sep=',', encoding='utf-8')
incrim+=1
Получаем файл с корреляциями по текущей бумаге (типа corr_A.csv) и прошлым периодом по иным ценным бумагам (B, C, D их всего 90), для этого удаляем первую строку с пустыми значениями в файле типа securities_A.csv; Рассчитываем корреляции других ценных бумаг по отношению к текущей. Сортируем столбец корреляций и именований к ним. Сохраняем столбец корреляций по текущей ценной бумаге как отдельный DataFrame.
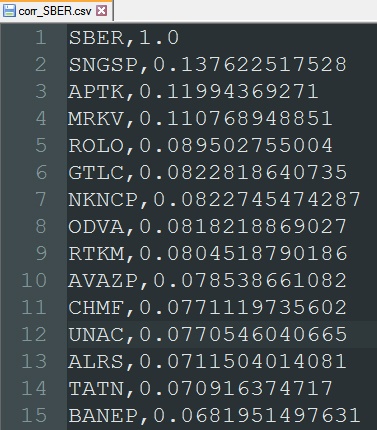
Поочередно каждый из файлов с корреляциями типа corr_A.csv «сливаем» в один общий файл – _quotes_data_end.csv.csv. Строки в данном файле обезличены. Можно наблюдать лишь величины отсортированных корреляций.
incrim=0
all_corr_Files = glob.glob("corr_*.csv")
list_corr = []
quotes_data_end = pd.DataFrame()
for file_corr in all_corr_Files:
df_corr = pd.read_csv(file_corr,index_col=None, header=0)
columns_corr = df_corr.columns
temp_header = columns_corr[0]
quotes_data_end[str(temp_header)]=df_corr.iloc[:,1]
incrim+=1
quotes_data_end.to_csv("_quotes_data_end.csv", sep=',', encoding='utf-8')
plt.figure();
quotes_data_end.plot();
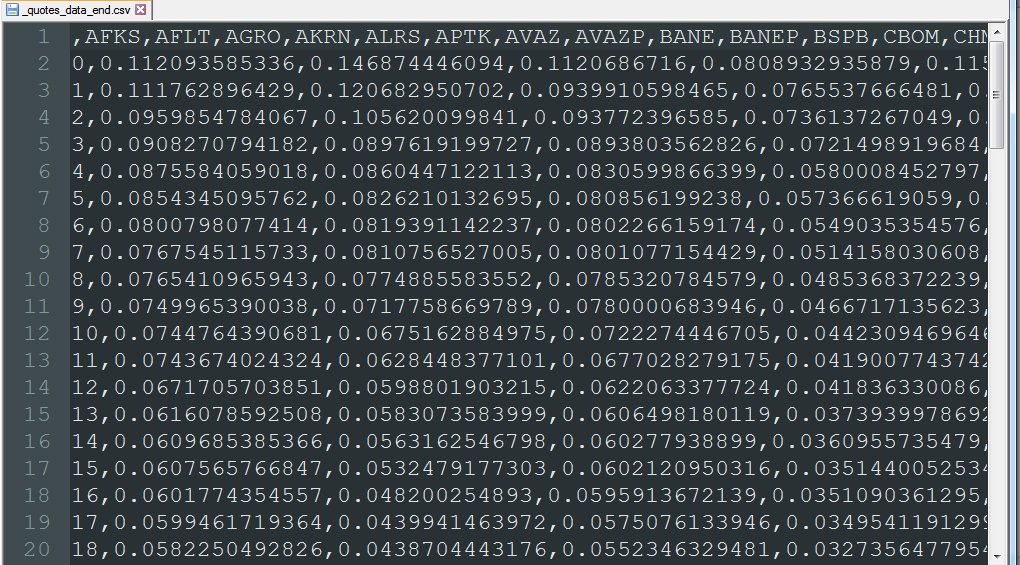
По полученным данным _quotes_data_end.csv строим график:
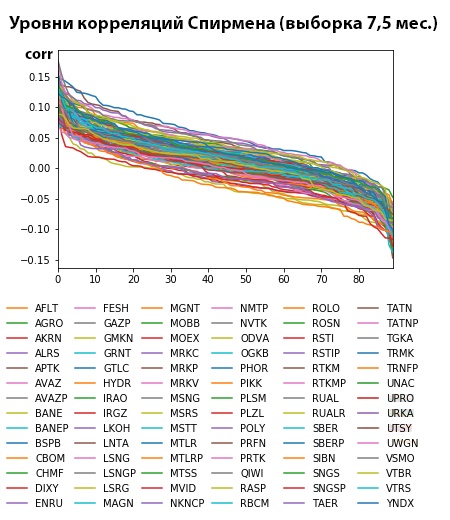
Уровень корреляций даже на крайних областях не высок. Основная масса корреляционных значений находится в пределах -0.15;0.15. Как таковых ценных бумаг, которые бы «вели» какие-либо другие финансовые инструменты в рамках рассматриваемого периода (7,5 мес) и на данном таймфрейме («часовиках») нет. Напомню, что в нашем распоряжении данные по 91 ценной бумаге. Но… если попытаться провести обработку тех же «часовиков» за более короткий период? По выборке длительностью в 1 месяц получим следующий график:
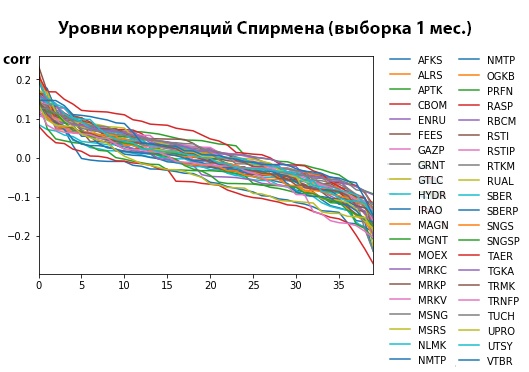
Снижение таймфрейма и уменьшение размера рассматриваемых выборок дает более высокие корреляции. Миф о «локомотивных» движениях (когда одна бумага «тянет» за собой другую, либо выступает «противовесом»)… превращается в реальность. Данный эффект наблюдается по мере уменьшения масштабов выборки. Однако, как оборотная сторона медали — увеличение значений корреляций при этом, сопровождается все более их нестабильным поведением. Бумага из «локомотива» может превратиться в «ведомую» за относительно короткий промежуток времени. Можем констатировать, что методы обработки данных нами были освещены, ответы на поставленные выше вопросы получены.
Каков же характер динамики изменения корреляций; того как это происходит и чем сопровождается? Но… это тема для продолжения.
Спасибо за внимание!
Автор: optimusqp
