Известная как минимум с 19 века задача коммивояжера имеет множество способов решения и неоднократно описана. Ее оптимизационная версия является NP-трудной, поэтому оптимальное решение можно получить либо полным перебором, либо оптимизированным полным перебором — методом ветвей и границ.
Пытаясь запрограммировать алгоритм Литтла (частный случай метода ветвей и границ), я понял, что в рунете крайне трудно найти его правильное описание понятным языком и разобранную программную реализацию. Однако имеющиеся в изобилии описания обманчиво правдоподобны на данных малого размера и с трудом проверяются без визуализации.

Метод ветвей и границ
Алгоритм Литтла является частным случаем МВиГ, т.е. в худшем случае его сложность равна сложности полного перебора. Теоретическое описание выглядит следующим образом:
Имеется множетво S всех гамильтоновых циклов рафа. На каждом шаге в S ищется ребро (i, j), исключение которого из маршрута максимально увеличит оценку снизу. Далее происходит разбиение множества на два непересекающихся S1 и S2. S1 — все циклы, содержащие ребро (i, j) и не содержащие (j, i). S2 — все циклы, не содержащие (i, j). Далее вычисляется оценка снизу для длины пути каждого множества и, если она превышает длину уже найденного решения, множество отбрасывается. Если нет — множества S1 и S2 обрабатываются так же, как и S.
Алгоритмическое описание
Имеется матрица расстояний M. Диагональ заполняется бесконечными значениями, т.к. не должно возникать преждевременных циклов. Также имеется переменная, хранящая нижнюю границу.
Стоит оговориться, что нужно вести учет двух видов бесконечностей — одна добавляется после удаления строки и столбца из матрицы, чтобы не возникало преждевременных циклов, другая — при отбрасывании ребер. Случаи будут рассмотрены чуть позже. Первую бесконечность обозначим как inf1, вторую — inf2. Диагональ заполнена inf1.
- Из каждого элемента каждой строки вычитается минимальный элемент данной строки. При этом минимальный элемент строки прибавляется к нижней границе
- Из каждого столбца аналогично вычитается минимальный элемент и прибавляется к нижней границе.
- Для каждого нулевого элемента M(i, j) вычисляется коэффициент, равный сумме минимальных элементов строки i и столбца j, исключая сам элемент (i, j). Этот коэффициент показывает, насколько гарантированно увеличится нижняя граница решения, если исключить из него ребро (i, j)
- Ищется элемент с максимальным коэффициентом. Если их несколько, можно выбрать любой (все равно оставшиеся будут рассмотрены на следующих шагах рекурсии)
- Рассматриваются 2 матрицы — M1 и M2. M1 равна M с удаленными строкой i и столбцом j. В ней находится столбец k и строка l, в которых не содержится inf1 и элемент M(k, l) приравнивается inf1. Как было сказано ранее, это необходимо во избежание преждевременных циклов (т.е. на первых этапах (k, l) == (j, i)). Матрица M1 соответствует множеству, сожержащему ребро (i, j). Вместе с удалением столбца и строки ребро (i, j) включается в путь.
- M2 равна матрице M, у которой элемент (i, j) равен inf2. Матрица соответствует множетсву путей, не сожержащих ребро (i, j) (важно понимать, что ребро (j, i) при этом не исключается).
- Переход к п.1 для матриц M1 и M2.
Эвристика состоит в том, что у матрицы M1 нижняя граница не больше, чем у матрицы M2 и в первую очередь рассматривается ветвь, содержащая ребро (i, j).
Пример
Примеров в интернете огромное количество, но действительно интересный находится в этой статье с хорошо иллюстированными деревьями (единственная найденная мной статья, в которой также указано про распространенную ошибку, но, к сожалению, в ней недостаточно алгоритмическое описание алгоритма — сначала про матрицы, потом про множества). Интересен пример тем, что если рассматривать только ветки с ребрами с максимальным штрафом, будет получен неверный результат.
Так что приведу шаги поиска оптимального пути для этой матрицы.
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | inf | 20 | 18 | 12 | 8 |
| 1 | 5 | inf | 14 | 7 | 11 |
| 2 | 12 | 18 | inf | 6 | 11 |
| 3 | 11 | 17 | 11 | inf | 12 |
| 4 | 5 | 5 | 5 | 5 | inf |
0 1 2 3 4
0 inf1 20.00 18.00 12.00 8.00
1 5.00 inf1 14.00 7.00 11.00
2 12.00 18.00 inf1 6.00 11.00
3 11.00 17.00 11.00 inf1 12.00
4 5.00 5.00 5.00 5.00 inf1
After subtracting:
0 1 2 3 4
0 inf1 12.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 12.00 inf1 0.00 5.00
3 0.00 6.00 0.00 inf1 1.00
4 0.00 0.00 0.00 0.00 inf1
edge (4, 1)
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 2.00 inf1
2 6.00 inf1 0.00 5.00
3 0.00 0.00 inf1 1.00
After subtracting:
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 2.00 inf1
2 6.00 inf1 0.00 5.00
3 0.00 0.00 inf1 1.00
edge (3, 2)
0 3 4
0 inf1 4.00 0.00
1 0.00 2.00 inf1
2 6.00 inf1 5.00
After subtracting:
0 3 4
0 inf1 2.00 0.00
1 0.00 0.00 inf1
2 1.00 inf1 0.00
edge (0, 4)
0 3
1 inf1 0.00
2 1.00 inf1
candidate solution(4 1) (3 2) (0 4) (1 3) (2 0)
cost: 43; record: 1.79769e+308
NEW RECORD
0 3 4
0 inf1 2.00 0.00
1 0.00 0.00 inf1
2 1.00 inf1 0.00
not edge (0, 4)
0 3 4
0 inf1 2.00 inf2
1 0.00 0.00 inf1
2 1.00 inf1 0.00
After subtracting:
0 3 4
0 inf1 0.00 inf2
1 0.00 0.00 inf1
2 1.00 inf1 0.00
limit: 44; record:43
DISCARDING BRANCH
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 2.00 inf1
2 6.00 inf1 0.00 5.00
3 0.00 0.00 inf1 1.00
not edge (3, 2)
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 2.00 inf1
2 6.00 inf1 0.00 5.00
3 0.00 inf2 inf1 1.00
After subtracting:
0 2 3 4
0 inf1 1.00 4.00 0.00
1 0.00 0.00 2.00 inf1
2 6.00 inf1 0.00 5.00
3 0.00 inf2 inf1 1.00
limit: 44; record:43
DISCARDING BRANCH
0 1 2 3 4
0 inf1 12.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 12.00 inf1 0.00 5.00
3 0.00 6.00 0.00 inf1 1.00
4 0.00 0.00 0.00 0.00 inf1
not edge (4, 1)
0 1 2 3 4
0 inf1 12.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 12.00 inf1 0.00 5.00
3 0.00 6.00 0.00 inf1 1.00
4 0.00 inf2 0.00 0.00 inf1
After subtracting:
0 1 2 3 4
0 inf1 6.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 6.00 inf1 0.00 5.00
3 0.00 0.00 0.00 inf1 1.00
4 0.00 inf2 0.00 0.00 inf1
edge (3, 1)
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 inf1 6.00
2 6.00 inf1 0.00 5.00
4 0.00 0.00 0.00 inf1
After subtracting:
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 inf1 6.00
2 6.00 inf1 0.00 5.00
4 0.00 0.00 0.00 inf1
edge (0, 4)
0 2 3
1 0.00 9.00 inf1
2 6.00 inf1 0.00
4 inf1 0.00 0.00
After subtracting:
0 2 3
1 0.00 9.00 inf1
2 6.00 inf1 0.00
4 inf1 0.00 0.00
edge (0, 0)
2 3
2 inf1 0.00
4 0.00 inf1
candidate solution(3 1) (0 4) (1 0) (2 3) (4 2)
cost: 41; record: 43
NEW RECORD
0 2 3
1 0.00 9.00 inf1
2 6.00 inf1 0.00
4 inf1 0.00 0.00
not edge (1, 0)
0 2 3
1 inf2 9.00 inf1
2 6.00 inf1 0.00
4 inf1 0.00 0.00
After subtracting:
0 2 3
1 inf2 0.00 inf1
2 0.00 inf1 0.00
4 inf1 0.00 0.00
limit: 56; record:41
DISCARDING BRANCH
0 2 3 4
0 inf1 10.00 4.00 0.00
1 0.00 9.00 inf1 6.00
2 6.00 inf1 0.00 5.00
4 0.00 0.00 0.00 inf1
not edge (0, 4)
0 2 3 4
0 inf1 10.00 4.00 inf2
1 0.00 9.00 inf1 6.00
2 6.00 inf1 0.00 5.00
4 0.00 0.00 0.00 inf1
After subtracting:
0 2 3 4
0 inf1 6.00 0.00 inf2
1 0.00 9.00 inf1 1.00
2 6.00 inf1 0.00 0.00
4 0.00 0.00 0.00 inf1
limit: 50; record:41
DISCARDING BRANCH
0 1 2 3 4
0 inf1 6.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 6.00 inf1 0.00 5.00
3 0.00 0.00 0.00 inf1 1.00
4 0.00 inf2 0.00 0.00 inf1
not edge (3, 1)
0 1 2 3 4
0 inf1 6.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 6.00 inf1 0.00 5.00
3 0.00 inf2 0.00 inf1 1.00
4 0.00 inf2 0.00 0.00 inf1
After subtracting:
0 1 2 3 4
0 inf1 0.00 10.00 4.00 0.00
1 0.00 inf1 9.00 2.00 6.00
2 6.00 0.00 inf1 0.00 5.00
3 0.00 inf2 0.00 inf1 1.00
4 0.00 inf2 0.00 0.00 inf1
limit: 47; record:41
DISCARDING BRANCH
Solution tour:
0 4 2 3 1 0
Tour length:
41Реализация
Шаг 1
Получение нулей в каждой строке и каждом столбце.
double LittleSolver::subtractFromMatrix(MatrixD &m) const {
// сумма всех вычтенных значений
double subtractSum = 0;
// массивы с минимальными элементами строк и столбцов
vector<double> minRow(m.size(), DBL_MAX),
minColumn(m.size(), DBL_MAX);
// обход всей матрицы
for (size_t i = 0; i < m.size(); ++i) {
for (size_t j = 0; j < m.size(); ++j)
// поиск минимального элемента в строке
if (m(i, j) < minRow[i])
minRow[i] = m(i, j);
for (size_t j = 0; j < m.size(); ++j) {
// вычитание минимальных элементов из всех
// элементов строки, кроме бесконечностей
if (m(i, j) < _infinity) {
m(i, j) -= minRow[i];
}
// поиск минимального элемента в столбце после вычитания строк
if ((m(i, j) < minColumn[j]))
minColumn[j] = m(i, j);
}
}
// вычитание минимальных элементов из всех
// элементов столбца, кроме бесконечностей
for (size_t j = 0; j < m.size(); ++j)
for (size_t i = 0; i < m.size(); ++i)
if (m(i, j) < _infinity) {
m(i, j) -= minColumn[j];
}
// суммирование вычтенных значений
for (auto i : minRow)
subtractSum += i;
for (auto i : minColumn)
subtractSum += i;
return subtractSum;
}Шаг 2
Увеличение нижней границы и сравнение ее с рекордом.
// вычитание минимальных элементов строк и столбцов
// увеличение нижней границы
bottomLimit += subtractFromMatrix(matrix);
// сравнение верхней и нижней границ
if (bottomLimit > _record) {
return;
}Шаг 3
Расчет коэффициентов.
double LittleSolver::getCoefficient(const MatrixD &m, size_t r, size_t c) {
double rmin, cmin;
rmin = cmin = DBL_MAX;
// обход строки и столбца
for (size_t i = 0; i < m.size(); ++i) {
if (i != r)
rmin = std::min(rmin, m(i, c));
if (i != c)
cmin = std::min(cmin, m(r, i));
}
return rmin + cmin;
}Поиск всех нулевых элементов и вычисление их коэффициентов.
// список координат нулевых элементов
list<pair<size_t, size_t>> zeros;
// список их коэффициентов
list<double> coeffList;
// максимальный коэффициент
double maxCoeff = 0;
// поиск нулевых элементов
for (size_t i = 0; i < matrix.size(); ++i)
for (size_t j = 0; j < matrix.size(); ++j)
// если равен нулю
if (!matrix(i, j)) {
// добавление в список координат
zeros.emplace_back(i, j);
// расчет коэффициена и добавление в список
coeffList.push_back(getCoefficient(matrix, i, j));
// сравнение с максимальным
maxCoeff = std::max(maxCoeff, coeffList.back());
}Шаг 4
Отбрасывание нулевых элементов с немаксимальными коэффициентами.
{ // область видимости итераторов
auto zIter = zeros.begin();
auto cIter = coeffList.begin();
while (zIter != zeros.end()) {
if (*cIter != maxCoeff) {
// если коэффициент не максимальный, удаление элемента из списка
zIter = zeros.erase(zIter);
cIter = coeffList.erase(cIter);
}
else {
++zIter;
++cIter;
}
}
}
return zeros;Шаг 5
Переход к множеству, содержащему ребро с максимальным штрафом.
auto edge = zeros.front();
// копия матрицы
auto newMatrix(matrix);
// из матрицы удаляются строка и столбец, соответствующие вершинам ребра
newMatrix.removeRowColumn(edge.first, edge.second);
// ребро iter добавляется к пути
auto newPath(path);
newPath.emplace_back(matrix.rowIndex(edge.first),
matrix.columnIndex(edge.second));
// добавление бесконечности для избежания преждевремнного цикла
addInfinity(newMatrix);
// обработка множества, содержащего ребро edge
handleMatrix(newMatrix, newPath, bottomLimit);Шаг 6
Переход к множеству, не содержащему ребро с максимальным штрафом.
// переход к множеству, не сожержащему ребро edge
// снова копирование матрицы текущего шага
newMatrix = matrix;
// добавление бесконечности на место iter
newMatrix(edge.first, edge.second) = _infinity + 1;
// обработка множества, не сожержащего ребро edge
handleMatrix(newMatrix, path, bottomLimit);Сравнение МВиГ с полным перебором
Несмотря на то, что метод ветвей и границ в худшем случае ничем не лучше полного перебора, в большинстве случаев он значительно выигрывает во времени благодаря эвристике для поиска начального решения и отбрасыванию заведомо плохих множеств.
Ниже представлены таблицы сравнения МВиГ с полным перебором и среднее время работы реализованного мной алгоритма на различном количестве городов. Тестировалось на матрицах для случайно сгенерированных точек.
Сравнение метода ветвей и границ с полным перебором.
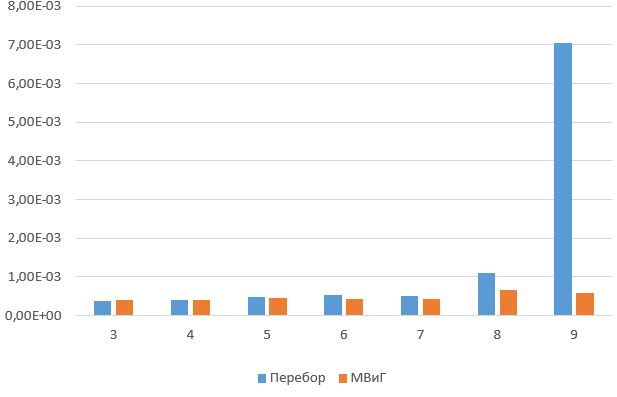
Начиная с 9 городов полный перебор заметно проигрывает МВиГ. Начиная с 13 городов полный перебор занимает больше минуты.
Время работы МВиГ на различном количестве городов.
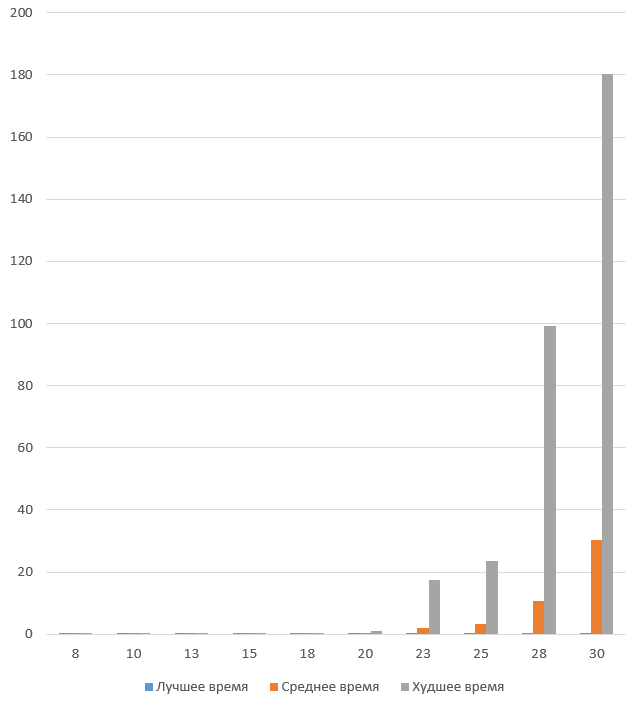
Графическое приложение
Также был сделан графический интерфейс на Qt с возможностью динамически смотреть на процесс решения. Как раз его рабочая область на гифке в шапке статьи. Итересующиеся могут скомпилировать и потрогать прогу руками.
Желтым цветом обозначен наилучший найденный путь и его длина находится в поле "Tour length".
Черным обозначены ребра, находящиеся в последнем просмотренном наборе.
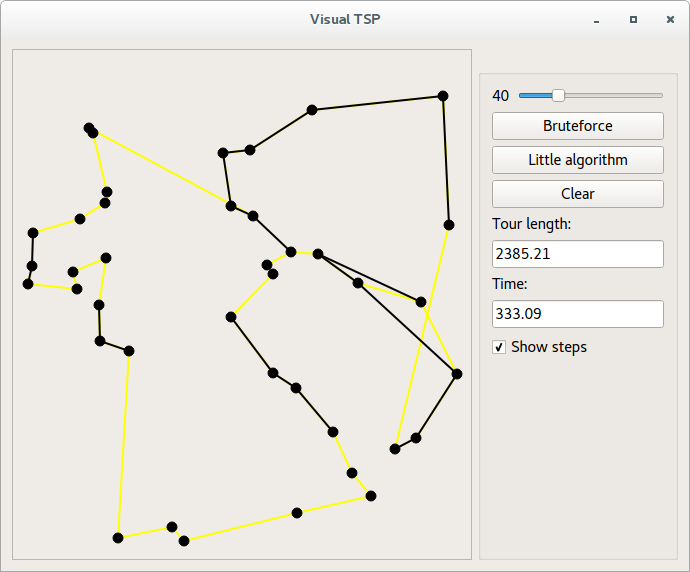
Для динамического отображения задача должна решаться либо пошагово, либо в параллельном с графическим интерфейсом потоке. Т.к. основная функция решения рекурсивна, был выбран второй вариант, из-за чего в решающий класс пришлось добавить мьютекс, а переменную рекорда сделать атомарной и в некоторых методах позаботиться о потокобезопасности.
Вместо заключения
Надеюсь, эта статья поможет тем, кто захочет реализовать данный алгоритм или уже реализовал и не понимает, почему он дает неверный результат.
Автор: scidev






![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс] Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75)