Работа с гетерогенными контейнерами с C++17

Привет! В последнее время много говорят о C++17, особенно с появлением в России национальной рабочей группы по стандартизации. На просторах сети без особых проблем можно найти короткие примеры использования последнего стандарта C++. Всё бы хорошо, но по настоящему обширного перехода на новые стандарты не наблюдается. Поэтому можем наблюдать картину, в которогй любая библиотека, требующая минимум 14 стандарта уже считается modern постфактум.

В данной публикации разработаем небольшую библиотеку (3 функции (apply, filter, reduce) и одна как «домашнее задание» (map) :)) по удобной работе с гетерогенными контейнерами в рантайме (гетерогенность за счёт std::variant из 17 стандарта).

Из нового, помимо новых библиотечных типов, попробуем на вкус fold expressions и совсем немного structured binding

Введение

Для начала небольшое введение в тему гетерогенных контейнеров. Как известно, настоящих гетерогенных контейнеров, работающих в рантайме на c++ нет. В нашем распоряжении есть std::tuple, следы которого практически полностью исчезают в рантайме (not pay for what you don't use) и… впрочем всё. Всё остальное — лишь строительные блоки для построения собственных велосипедов библиотек.

Стоительных блока, которые позволяют нам сделать гетерогенный контейнер два — std::any и std::variant. Первый не помнит тип, поэтому его использование сильно ограничено. std::variant помнит тип и умеет матчить функторы на текущий тип с помощью std::visit (реализовано с помощью генерации таблицы методов и последующих переходов по ней). Реализация поистине магическая, а магия — единственное, что поможет сделать то, что сделать на первый взгляд невозможно :) (конечно возможно, ведь на c++ возможно всё). Внутри std::variant содержит не так много оверхеда, перенося boost версию в стандарт разработчики позаботились о производительности (относительной того, что было). Резюмируя, берём std::variant в качестве контейнера типов и базовой единицы гетерогенного контейнера.

Дисклеймер

Заранее предупреждаю о максимальной компактности кода. Не стоит бездумно его копировать, он был максимально облёгчён для быстрого понимания. Нет пространств имён, форвардинга ссылок и ещё много чего.

Так же не претендую на уникальность, наверняка есть подобные хорошие библиотеки :)

Начало

Для более лёгкого понимания и тестирования функций возьмём простой пример. Для этого проэмулируем обычную полиморфную структуру:

struct Circle
{
    void Print() { cout << "Circle. " << "Radius: " << radius << endl; }
    double Area() { return 3.14 * radius * radius; }

    double radius;
};

struct Square
{
    void Print() { cout << "Square. Side: " << side << endl; }
    double Area() { return side * side * side * side; }

    double side;
};

struct EquilateralTriangle
{
    void Print() { cout << "EquilateralTriangle. Side: " << side << endl; }
    double Area() { return (sqrt(3) / 4) * (side * side); }

    double side;
};

using Shape = variant<Circle, Square, EquilateralTriangle>;

Так же для сравнения будем держать в уме её простой полиморфный аналог:

struct Shape
{
    virtual void Print() = 0;
    virtual double Area() = 0;
    virtual ~Shape() {};
};

struct Circle : Shape
{
    Circle(double val) : radius(val) {}

    void Print() override { cout << "Circle. " << "Radius: " << radius << endl; }
    double Area() override { return 3.14 * radius * radius; }

    double radius;
};

struct Square : Shape
{
    Square(double val) : side(val) {}

    void Print() override { cout << "Square. Side: " << side << endl; }
    double Area() override { return side * side * side * side; }

    double side;
};

struct EquilateralTriangle : Shape
{
    EquilateralTriangle(double val) : side(val) {}

    void Print() override { cout << "EquilateralTriangle. Side: " << side << endl; }
    double Area() override { return (sqrt(3) / 4) * (side * side); }

    double side;
};

Создадим вектор и попытаемся стандартными средствами добиться полиморфного поведения. Проитерируемся по вектору и вызовем функцию Print.

Для начала возьмём динамический аналог (на виртуальных функциях). Как можно думать, никаких проблем с динамическим полиморфизмом у нас нет:

vector<Shape*> shapes;
shapes.emplace_back(new Square(8.2));
shapes.emplace_back(new Circle(3.1));
shapes.emplace_back(new Square(1.8));
shapes.emplace_back(new EquilateralTriangle(10.4));
shapes.emplace_back(new Circle(5.7));
shapes.emplace_back(new Square(2.9));

Однако выглядит не очень современно. Голые вызовы new не внушают доверия. Перепишем:

vector<shared_ptr<Shape>> shapes;
shapes.emplace_back(make_shared<Square>(8.2));
shapes.emplace_back(make_shared<Circle>(3.1));
shapes.emplace_back(make_shared<Square>(1.8));
shapes.emplace_back(make_shared<EquilateralTriangle>(10.4));
shapes.emplace_back(make_shared<Circle>(5.7));
shapes.emplace_back(make_shared<Square>(2.9));

Теперь выглядит лучше. Однако для новичка понятности в коде явно не прибавилось. Но не будем разводить холивар, выполним нашу задачу:

for (shared_ptr<Shape> shape: shapes)
{
    shape->Print();
}

// Вывод:
// Square. Side: 8.2
// Circle. Radius: 3.1
// Square. Side: 1.8
// EquilateralTriangle. Side: 10.4
// Circle. Radius: 5.7
// Square. Side: 2.9

Так же попробуем реализовать схожее поведение для гетерогенного контейнера:

vector<Shape> operations;
operations.emplace_back(EquilateralTriangle { 5.6 });
operations.emplace_back(Square { 8.2 });
operations.emplace_back(Circle { 3.1 });
operations.emplace_back(Square { 1.8 });
operations.emplace_back(EquilateralTriangle { 10.4 });
operations.emplace_back(Circle { 5.7 });
operations.emplace_back(Square { 2.9 });

Здесь уже никаких указателей. Без проблем можно работать с объектами на стеке. Так же вместо коструктора можно использовать aggregate initialization для в «меру простых» типов.

Однако просто проитерироваться и вызвать функцию уже не удастся. Попробуем сделать это средствами, которые предоставляет std::variant. Для этого имеем функцию std::visit, так же нужно создать класс функторов.

Всё будет выглядеть подобным образом:

struct Visitor
{
    void operator()(Circle& c) { c.Print(); }
    void operator()(Square& c) { c.Print(); }
    void operator()(EquilateralTriangle& c) { c.Print(); }
};

...
...
...

for (Shape& shape: shapes)
{
    visit(Visitor{}, shape);
}

Вывод аналогичный. Так же такое же поведение можно проэмулировать с помощью constexpr if. Здесь уже кому что больше нравится.

Познакомившись с функционалом, который предоставляет нам стандартная библиотека, попробуем немного упростить работу с гетерогенными последовательностями.

Реализуем самые частые и всеобъемлющие функции: apply, filter, reduce.

Шаг 1

Для начала упростим себе задачу. Первый шаг достаточно притивен — описывался уже не раз.
Возьмём variadic templates, механизм наследования и знание о том, что лямбда-функции разворачиваются в обычные стуктуры — функторы. Унаследуемся от набора лябмд и создадим функцию, которая поможет нам вывести шаблонные типы:

template < typename... Func >
class Visitor : Func... { using Func::operator()...; }
template < class... Func > make_visitor(Func...) -> Visitor < Func... >;

Теперь вместо создания классов с функторами мы можем пользоваться набором лямбд, которые будут матчится по своим сигнатурам:

for (Shape& shape: shapes)
{
    visit(make_visitor(
                        []](Circle& c) { c.Print(); },
                        []](Square& c) { c.Print(); },
                        []](EquilateralTriangle& c) { c.Print(); }
                      ), shape);
}

Также можем воспользоваться выводом типов с generic параметром:

for (Shape& shape: shapes)
{
    visit(make_visitor([]](auto& c) { c.Print(); }), shape);
}

Получилось достаточно симпатично и в меру коротко.

Apply

Осталось собрать всё вместе и получить функцию apply для гетерогенных последовательностей:

template <
           typename InputIter,
           typename InputSentinelIter,
           typename... Callable
         >
void apply(InputIter beg,
           InputSentinelIter end,
           Callable... funcs)
{
    for (auto _it = beg; _it != end; ++_it)
        visit(make_visitor(funcs...), *_it);
};

Готово. Показанная техника на новизну не претендует, любой разработчик, так или иначе работавший с boost::variant давно реализовал для себя нечто подобное http://en.cppreference.com/w/cpp/utility/variant/visit, https://habrahabr.ru/post/270689/).

Теперь мы можем использовать функцию подобным образом:

apply(shapes.begin(), shapes.end(), [](auto& shape) { shape.Print(); });

или

apply(shapes.begin(), shapes.end(), 
      [] (Circle& shape)              { shape.Print(); },
      [] (Square& shape)              { shape.Print(); },
      [] (EquilateralTriangle& shape) { shape.Print(); });

Как видите, получилось довольно непохо. Однако, если мы передадим функторы не для всех типов, которые есть в std::variant, получится ошибка компиляции. Чтобы избежать этого, по подобию SFINAE сделаем функтор с elipsis, который будет вызываться при отсутствии любой другой альтернативы, причём в порядке вызова он будет самым последним вариантом.

template <
           typename InputIter,
           typename InputSentinelIter,
           typename... Callable
         >
void apply(InputIter beg,
           InputSentinelIter end,
           Callable... funcs)
{
    for (auto _it = beg; _it != end; ++_it)
        visit(make_visitor(funcs..., [](...){}), *_it);
};

Теперь можем передавать функторы не для всех типов, для отсутствующих будет произведён вызов пустой лямбды:

// Выводит информацию только для типов Circle
apply(shapes.begin(), shapes.end(), [] (Circle& shape) { shape.Print(); }); 

Для наглядного примера просто покажу, как сделать подобное с помощью динамического полиморфизма:

// Выводит информацию только для типов Circle
for_each(shapes.begin(), shapes.end(),
         [] (shared_ptr<Shape> shape) {
             if (dynamic_pointer_cast<Circle>(shape))
                    shape->Print();
         });

Далеко не самый приятный вид.

Filter

По аналогии сделаем функцию filter. Смысловая нагрузка практически не отличается кроме того, что лямбда, имеющая elipsis в сигнатуре должна возвращать значение типа bool. Будем считать, что если мы не передали функтор, обрабатывающих какой то конкретный тип, то мы не хотим его видеть его экземпляры отфильтрованном контейнере.

template <
           typename InputIter,
           typename InputSentinelIter,
           typename OutputIter,
           typename... Callable
         >
void filter(InputIter beg,
            InputSentinelIter end,
            OutputIter out,
            Callable... funcs)
{
    for (auto _it = beg; _it != end; ++_it)
    {
        if (visit(make_visitor(funcs..., [] (...) { return false; }), 
                  *_it))
            *out++ = *_it;
    }
};

Пользоваться реализованной функцией можно следующим образом:

vector<Shape> filtered;
filter(shapes.begin(), shapes.end(),
       back_inserter(filtered),
       [] (Circle& c) { return c.radius > 4.; },
       [] (Square& s) { return s.side < 5.; });

apply(filtered.begin(), filtered.end(), [](auto& shape) { shape.Print(); });

// Вывод:
// Square. Side: 1.8
// Circle. Radius: 5.7
// Square. Side: 2.9

Аналог, реализованный с помощью динамического полиморфизма:

vector<shared_ptr<Shape>> filtered;
copy_if(shapes.begin(), shapes.end(),
        back_inserter(filtered),
        [] (shared_ptr<Shape> shape)
        {
            if (auto circle = dynamic_pointer_cast<Circle>(shape))
            {
                return circle->radius > 4.;
            }
            else if (auto square = dynamic_pointer_cast<Square>(shape))
            {
                return square->side < 5.;
            }
            else return false;
        });

for_each(filtered.begin(), filtered.end(), [](shared_ptr<Shape> shape) { shape->Print(); });

// Вывод:
// Square. Side: 1.8
// Circle. Radius: 5.7
// Square. Side: 2.9

Reduce

Осталось реализовать reduce (аналог std::accumulate) и map (аналог std::transform). Реализация этих функций несколько сложнее, чем это было с apply и filter. Для reduce мы используем функторы с двумя параметрами (значение аккумулятора и сам объект). Для того, чтобы реализовать схожее поведение, можно частично применить лямбда функции таким образом, чтобы для std::variant остались функции одного аргумента. Красивого решения для c++ по частичному применению нет, быстрый способ — захват необходимого контекста с помощью другой лямбды. Учитывая, что мы работаем не с одной лямбдой, а с variadic pack, код раздувается и начинает быть плохо читаемым. Спасает нас обработка вариадиков с помощью fold expressions. Ветераны знают, какими костылями приходилось раньше сворачивать списки типов.

template <
           typename InputIter,
           typename InputSentinelIter,
           typename AccType,
           typename... Callable
         >
struct reduce < InputIter, InputSentinelIter, AccType, false, Callable... >
{
    constexpr auto operator()(InputIter beg, InputSentinelIter end,
                              AccType initial_acc, Callable... funcs)
    {
        for (auto _it = beg; _it != end; ++_it)
        {
            initial_acc = visit(utility::make_overloaded_from_tup(
                tup_funcs(initial_acc, funcs...),
                make_index_sequence<sizeof...(Callable)>{},
                [&initial_acc] (...) { return initial_acc; } ),
                                *_it);
        }
        return initial_acc;
    }
};

Для того, чтобы сделать что то подобное, было решено воспользоваться старым добрым кортежем (std::tuple). Обработка его элементов не слишком сложная, в любой момент можно написать свою. И так, я создаю кортеж из лямбд, который трасформируется в новый кортеж путём оборачивания каждой лямбды в другую с захватом значения аккумулятора. Благо трансформация кортежа, используя новый стандарт, пишется относительно легко:

template < typename... Types, typename Func, size_t... I >
constexpr auto tuple_transform_impl(tuple<Types...> t, Func func, index_sequence<I...>)
{
    return make_tuple(func(get<I>(t)...));
}

template < typename... Types, typename Func >
constexpr auto tuple_transform(tuple<Types...> t, Func f)
{
    return tuple_transform_impl(t, f make_index_sequence<sizeof...(Types)>{});
}

Для того, чтобы создать объемлющую лябду, мне нужно знать тип второго аргумента приходящей лямбды. С помощью helper'ов, найденных на просторах интернета, можно скастовать лямбду к структуре, имеющей оператор вызова и путём матчинга получить желаемый тип.

Выглядит это всё примерно так:

template < typename Func, typename Ret, typename _, typename A, typename... Rest >
A _sec_arg_hlpr(Ret (Func::*)(_, A, Rest...));

template < typename Func >
using second_argument = decltype(_sec_arg_hlpr(&Func::operator()));

template < typename AccType, typename... Callable >
constexpr auto tup_funcs(AccType initial_acc, Callable... funcs)
{
    return tuple_transform(tuple<Callable...>{ funcs... },
        [&initial_acc](auto func) {
            return [&initial_acc, &func] (second_argument<decltype(func)> arg) {
                return func(initial_acc, arg); };
        });
}

Всё бы хорошо, но эти чудеса не работают с generic функциями, типы входных аргументов которых мы не можем получить по определению. Поэтому, используя tag dispatching и создав простенький трейт для проверки функции мы создаём для этого случая свою реализацию.
Резюмируя, получаем для reduce следующие возможности для использования:

using ShapeCountT = tuple<size_t, size_t, size_t>;
auto result = reduce(shapes.begin(), shapes.end(),
                     ShapeCountT{},
                     [] (ShapeCountT acc, Circle& item)
                     {
                         auto [cir, sq, tr] = acc;
                         return make_tuple(++cir, sq, tr);
                     },
                     [] (ShapeCountT acc, Square& item)
                     {
                         auto [cir, sq, tr] = acc;
                         return make_tuple(cir, ++sq, tr);
                     },
                     [] (ShapeCountT acc, EquilateralTriangle& item)
                     {
                         auto [cir, sq, tr] = acc;
                         return make_tuple(cir, sq, ++tr);
                     });
auto [cir, sq, tr] = result;
cout << "Circle count: " << cir
     << "tSquare count: " << sq
     << "tTriangle count: " << tr << endl;

// Вывод:
// Circle count: 2 Square count: 3 Triangle count: 2

Функция map реализуется на базе похожих идей, описание её реализации и саму реализацию опущу. Для тренировки своих meta скиллов предлагаю реализовать её самим :)

Что дальше?

Немного об ошибках. Сделаем шаг в сторону и увидим подобное сообщение:

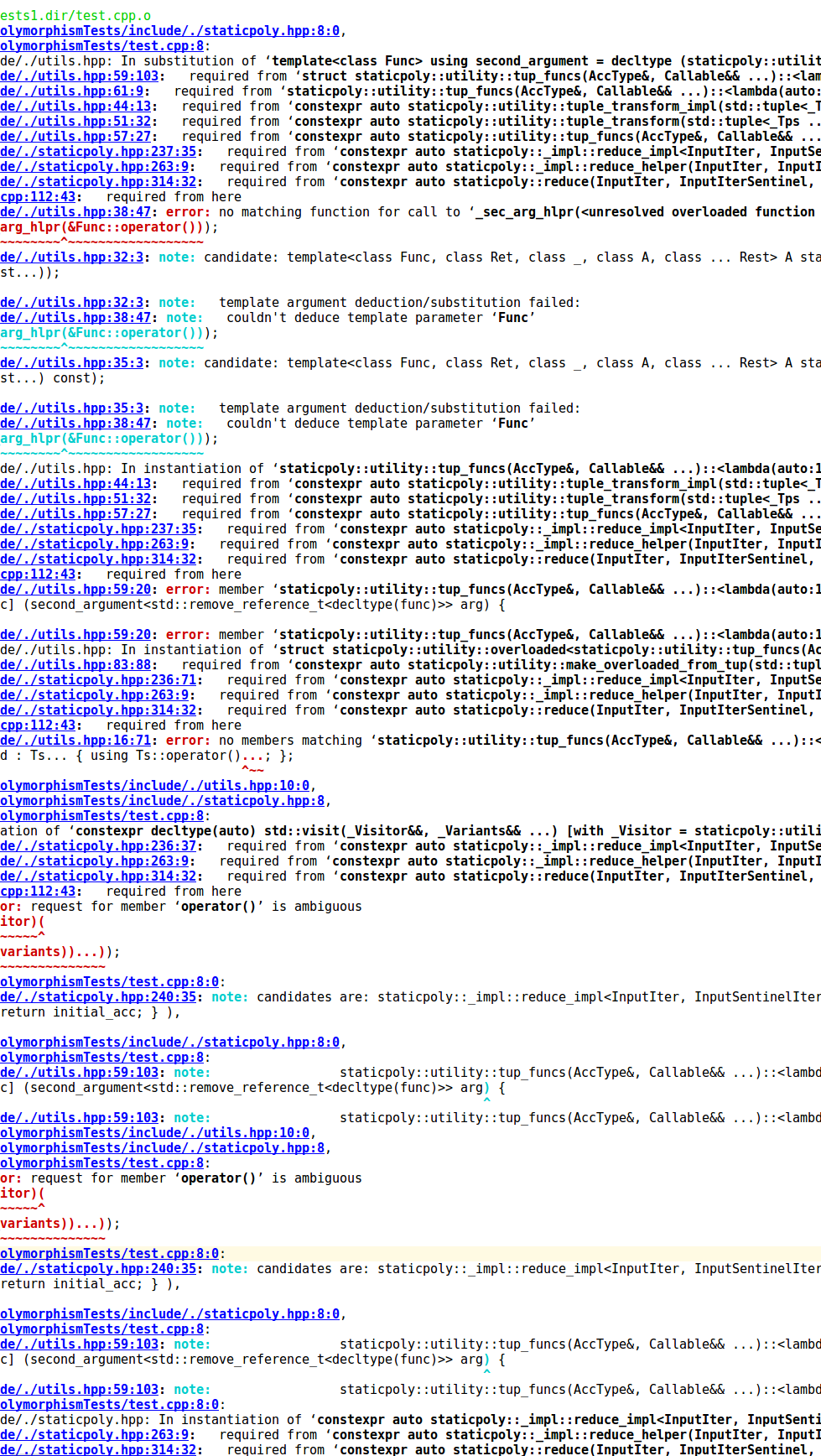
Текст этой ошибки не удастся разобрать, даже если вы используете очень простой код (ошибка заключается в неправильном использовании generic параметра функтора). Представьте что будет, если вы будете использовать классы намного сложнее представленных.

Есть несколько подходов, как можно элегантно или не очень сказать об истинной природе ошибки.
В следующей раз разбавим написанное с Concepts TS из gcc-7.1.

Резюмируя, можно сказать, что подобный подход может сильно пригодиться для работы с библиотеками, которым приходилось использовать TypeErasure технику, для шаблонных классов с разной специализацией, для примитивной эмуляции полиморфизма,…

А как бы дополнили / использовали этот функционал вы? Пишите в комментариях, будет интересно почитать

Вышеприведённый код доступен тут.

Автор: JegernOUTT

Источник