Деревья. Кратко напомним
Дерево – частный случай графа. Деревья широко применяются в программировании. Дерево – это связный граф без циклов. Дерево называется помеченным, если каждой вершине соответствует уникальная метка. Обычно это число.
Определение. Построение кода Прюфера для заданного дерева
Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n вершинами с помощью последовательности n-2 целых чисел в отрезке [1,n]. То есть, можно сказать, что код Прюфера – это биекция между всеми остовными деревьями полного графа и числовыми последовательностями.
Данный способ кодирования деревьев был предложен немецким математиком Хайнцом Прюфером в 1918 году.
Рассмотрим алгоритм построения кода Прюфера для заданного дерева с n вершинами.
На вход подается список ребер. Выбирается лист дерева с наименьшим номером, затем он удаляется из дерева, и к коду Прюфера добавляется номер вершины, которая была связана с этим листом. Эта процедура повторяется n-2 раза. В конце концов, в дереве останется только 2 вершины, и алгоритм на этом завершается. Номера оставшихся двух вершин в код не записываются.
Таким образом, код Прюфера для заданного дерева – это последовательность из n-2 чисел, где каждое число – номер вершины, связанной с наименьшим на тот момент листом – то есть это число в отрезке [1,n].
Пример
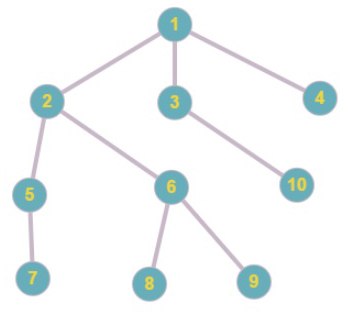
Исходное дерево
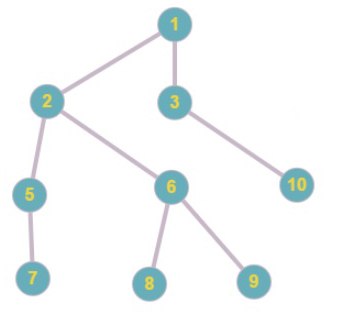
Код Прюфера: 1
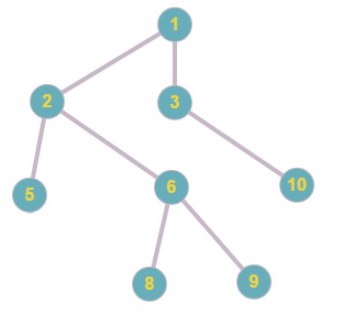
Код Прюфера: 1 5
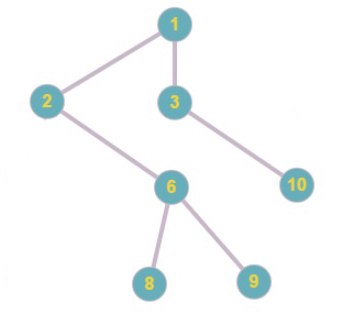
Код Прюфера: 1 5 2
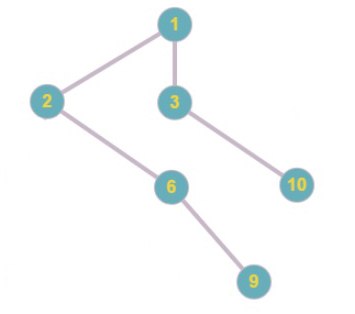
Код Прюфера: 1 5 2 6
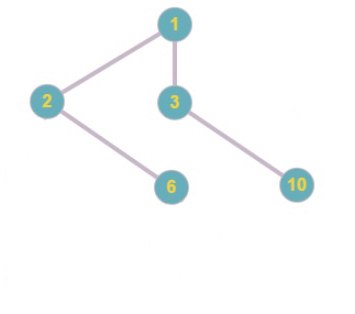
Код Прюфера: 1 5 2 6 6
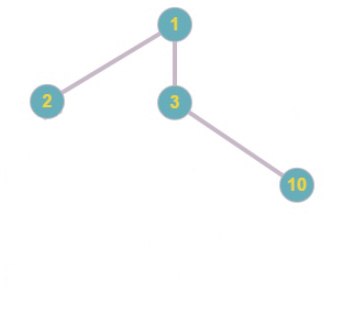
Код Прюфера: 1 5 2 6 6 2
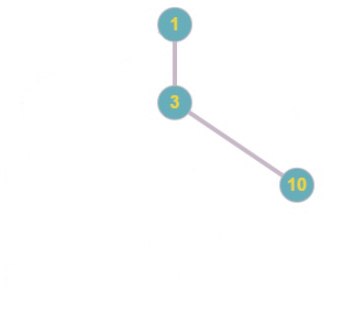
Код Прюфера: 1 5 2 6 6 2 1
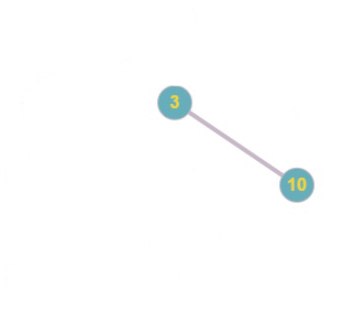
Код Прюфера: 1 5 2 6 6 2 1 3
Восстановление дерева по его коду Прюфера
Рядом с задачей построения кода Прюфера стоит задача восстановления закодированного дерева. Будем рассматривать алгоритм восстановления дерева со следующими условиями: на вход подается последовательность цифр (вершин), которая представляет код Прюфера, результатом будет список ребер дерева. Таким образом, задача будет решена.
Рассмотрим алгоритм декодирования подробно. Помимо кода нам нужен список всех вершин графа. Мы знаем, что код Прюфера состоит из n-2 вершин, где n – это число вершин в графе. То есть, мы можем по размеру кода определить число вершин в закодированном дереве.
В результате, в начале работы алгоритма мы имеем массив из кода Прюфера размера n-2 и массив всех вершин графа: [1… n]. Далее n-2 раза повторяется такая процедура: берется первый элемент массива, содержащего код Прюфера, и в массиве с вершинами дерева производится поиск наименьшей вершины, не содержащейся в массиве с кодом. Найденная вершина и текущий элемент массива с кодом Прюфера составляют ребро дерева. Данные вершины удаляются из соответствующих массивов, и описанная выше процедура повторяется, пока в массиве с кодом не закончатся элементы. В конце работы алгоритма в массиве с вершинами графа останется две вершины, они составляют последнее ребро дерева. В результате получаем список всех ребер графа, который был закодирован.
Пример
Восстановим дерево по коду Прюфера, который был получен в примере кодирования.
Первый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 4
Список ребер: 1 4
Второй шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 7
Список ребер: 1 4, 5 7
Третий шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 5
Список ребер: 1 4, 5 7, 2 5
Четвертый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 8
Список ребер: 1 4, 5 7, 2 5, 6 8
Пятый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 9
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9
Шестой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 6
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6
Седьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 2
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2
Восьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1
Завершение алгоритма
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1, 3 10
Заключение
Код Прюфера был предложен как наглядное и простое доказательство формулы Кэли о числе помеченных деревьев. На практике же его используют чаще для решения комбинаторных задач.
Источники
- Уилсон Р. Введение в теорию графов. Перевод с англ. М.: Мир, 1977. -208 с.
- Комбинаторика. Булевы функции. Графы: учеб. пособие / А. А. Балагура, О. В. Кузьмин. – Иркутск: Изд-во ИГУ, 2012. – 115 с.
- MAXimal [Электронный ресурс] — Режим доступа: ссылка, свободный. (дата обращения: 22.04.2017)
Автор: tanyasheli
