Автоэнкодеры в Keras, Часть 4: Conditional VAE

2017-06-26 в 10:25, admin, рубрики: autoencoder, deep learning, keras, machine learning, mnist, python, Алгоритмы, математика, машинное обучение, обработка изображений

Содержание

Часть 1: Введение
Часть 2: Manifold learning и скрытые (latent) переменные
Часть 3: Вариационные автоэнкодеры (VAE)
Часть 4: Conditional VAE
Часть 5: GAN (Generative Adversarial Networks) и tensorflow
Часть 6: VAE + GAN

В прошлой части мы познакомились с вариационными автоэнкодерами (VAE), реализовали такой на keras, а также поняли, как с его помощью генерировать изображения. Получившаяся модель, однако, обладала некоторыми недостатками:

Не все цифры получилось хорошо закодировать в скрытом пространстве: некоторые цифры либо вообще отсутствовали, либо были очень смазанными. В промежутках между областями, в которых были сконцентрированы варианты одной и той же цифры, находились вообще какие-то бессмысленные иероглифы.
Что тут писать, вот так выглядели сгенерированные цифры:
Картинка
Сложно было генерировать картинку какой-то заданной цифры. Для этого надо было смотреть, в какую область латентного пространства попадали изображения конкретной цифры, и сэмплить уже откуда-то оттуда, а тем более было сложно генерировать цифру в каком-то заданном стиле.

В этой части мы посмотрим, как можно лишь совсем немного усложнив модель преодолеть обе эти проблемы, и заодно получим возможность генерировать картинки новых цифр в стиле другой цифры – это, наверное, самая интересная фича будущей модели.

Автоэнкодеры в Keras, Часть 4: Conditional VAE - 2

Сначала подумаем о причинах 1-го недостатка:

Многообразия, на которых лежат различные цифры, могут быть далеко друг от друга в пространстве картинок. То есть сложно представить, как, например, непрерывно отобразить картинку цифры „5“, в картинку цифры „7“, при том, чтобы все промежуточные картинки можно было назвать правдоподобными. Таким образом, многообразие, около которого лежат цифры, вовсе не обязано быть линейно связанным. Автоэнкодер же, в силу того что является композицией непрерывных функций, сам может отображать в код и обратно только непрерывно, особенно если это вариационный автоэнкодер. В нашем предыдущем примере все усложнялось еще и тем, что автоэнкодер пытался искать двумерное многообразие.

В качестве иллюстрации вернемся к нашему искусственному примеру из 2-ой части, только сделаем определяющее многообразие несвязным:

Автоэнкодеры в Keras, Часть 4: Conditional VAE - 3

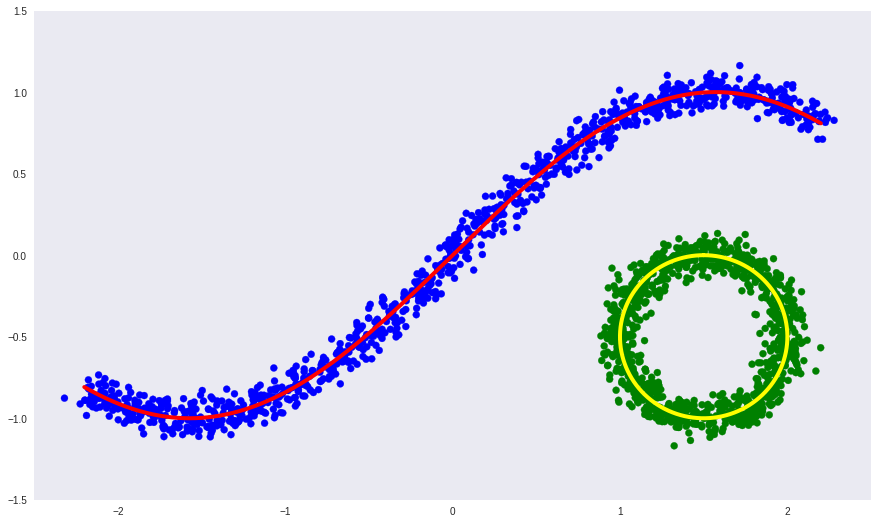
Здесь:

синие и зеленые точки — объекты выборки,
красная и желтая кривые — несвязанное определяющее многообразие.

Попробуем теперь выучить определяющее многообразие с помощью обычного глубокого автоэнкодера.

Код

# Импорт необходимых библиотек
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

# Создание датасета
x1 = np.linspace(-2.2, 2.2, 1000)
fx = np.sin(x1)
dots1 = np.vstack([x1, fx]).T

t = np.linspace(0, 2*np.pi, num=1000)
dots2 = 0.5*np.array([np.sin(t), np.cos(t)]).T + np.array([1.5, -0.5])[None, :]

dots = np.vstack([dots1, dots2])
noise = 0.06 * np.random.randn(*dots.shape)

labels = np.array([0]*1000 + [1]*1000)
noised = dots + noise


# Визуализация
colors = ['b']*1000 + ['g']*1000
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1],  color="red",    linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1],  color="yellow", linewidth=4)
plt.grid(False)

# Модель и обучение
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam

def deep_ae():
    input_dots = Input((2,))
    x = Dense(64, activation='elu')(input_dots)
    x = Dense(64, activation='elu')(x)
    code = Dense(1, activation='linear')(x)
    x = Dense(64, activation='elu')(code)
    x = Dense(64, activation='elu')(x)
    out = Dense(2, activation='linear')(x)

    ae = Model(input_dots, out)
    return ae

dae = deep_ae()
dae.compile(Adam(0.001), 'mse')
dae.fit(noised, noised, epochs=300, batch_size=30, verbose=2)

# Результат
predicted = dae.predict(noised)

# Визуализация
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1],  color="red",    linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1],  color="yellow", linewidth=4)
plt.scatter(predicted[:, 0], predicted[:, 1], c='white', s=50)
plt.grid(False)

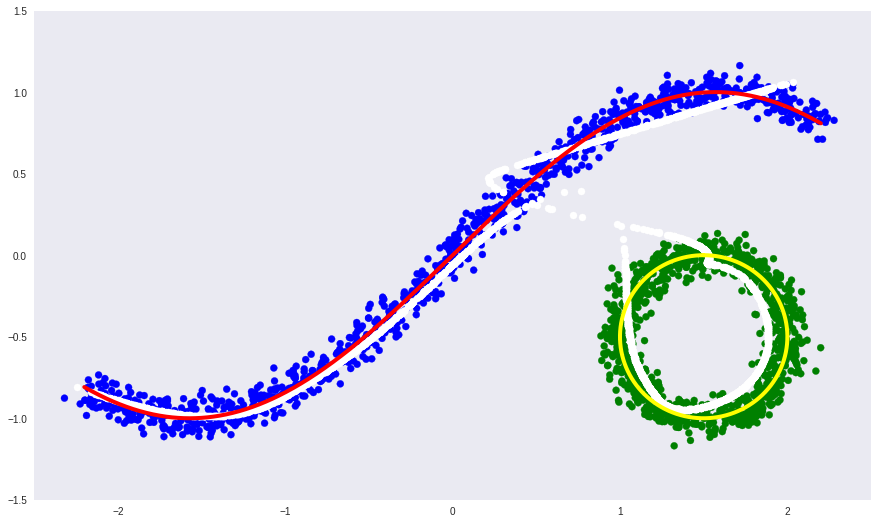
белая линия — многообразие в которое переходят синие и зеленые точки данных после автоэнкодера, то есть попытка автоэнкодера построить многообразие, определяющее больше всего вариации в данных.

Видно, что у простого автоэнкодера не получилось выучить форму несвязного многообразия. Вместо этого он хитро продолжил одно в другое.

Если же мы знаем лейблы данных, которые определяют на каком из частей несвязного многообразия лежат эти данные (как с цифрами), то мы можем просто condition автоэнкодер на этих лейблах. То есть просто дополнительно с данными подавать на вход энкодеру и декодеру еще и лейблы данных. В таком случае источником разрывности в данных будет лейбл, и это позволит автоэнкодеру выучить каждую часть линейно несвязного многообразия отдельно.

Посмотрим на тот же самый пример, только теперь на вход и энкодеру, и декодеру будем передавать дополнительно еще и лейбл.

Код

from keras.layers import concatenate

def deep_cond_ae():
    input_dots = Input((2,))
    input_lbls = Input((1,))
    full_input = concatenate([input_dots, input_lbls])
    x = Dense(64, activation='elu')(full_input)
    x = Dense(64, activation='elu')(x)
    code = Dense(1, activation='linear')(x)

    full_code = concatenate([code, input_lbls])
    x = Dense(64, activation='elu')(full_code)
    x = Dense(64, activation='elu')(x)
    out = Dense(2, activation='linear')(x)

    ae = Model([input_dots, input_lbls], out)
    return ae

cdae = deep_cond_ae()
cdae.compile(Adam(0.001), 'mse')
cdae.fit([noised, labels], noised, epochs=300, batch_size=30, verbose=2)


predicted = cdae.predict([noised, labels])

# Визуализация
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1],  color="red",    linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1],  color="yellow", linewidth=4)
plt.scatter(predicted[:, 0], predicted[:, 1], c='white', s=50)
plt.grid(False)

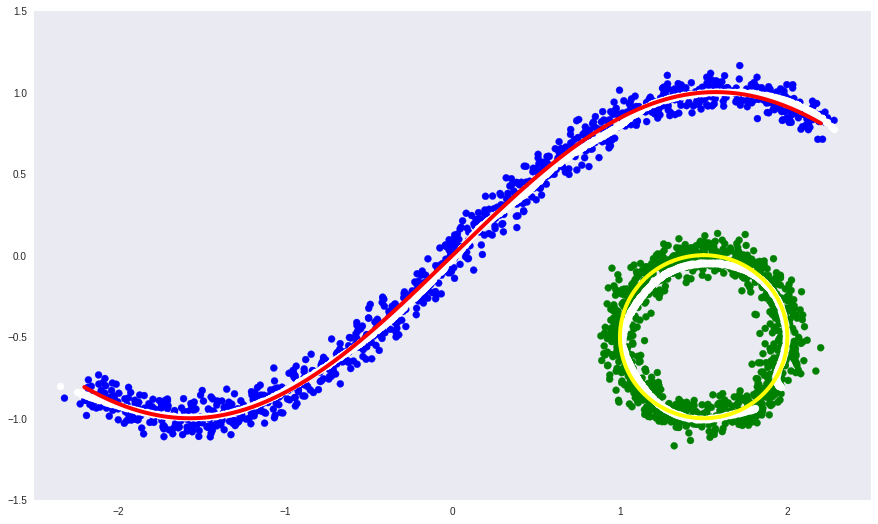
На этот раз автоэнкодеру удалось выучить линейно несвязное определяющее многообразие.

CVAE

Если же теперь взять VAE, как в предыдущей части, и подавать на вход еще и лейблы, то получится Conditional Variational Autoencoder (CVAE).

С картинками цифр получается вот так:
Автоэнкодеры в Keras, Часть 4: Conditional VAE - 6

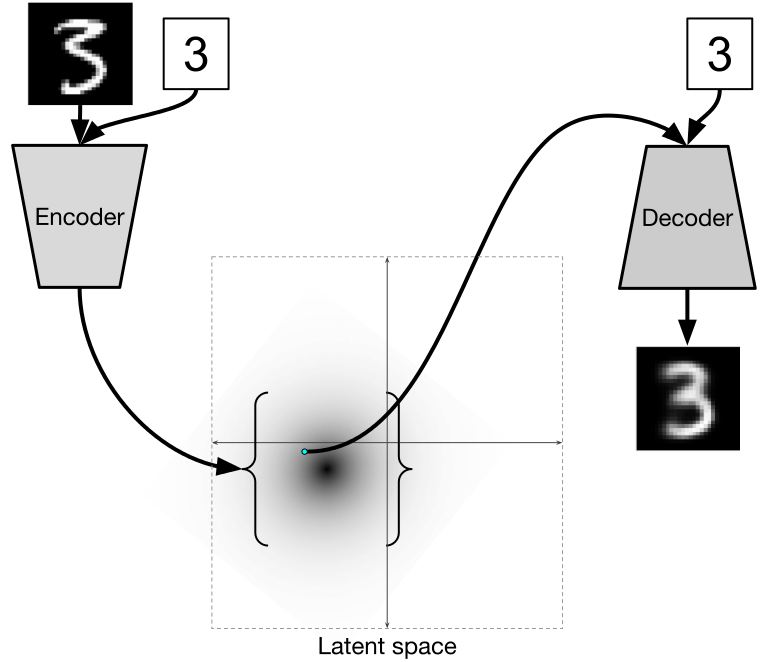
Картинка выше из [2]

В этом случае основное уравнение VAE из прошлой части становится просто conditioned на ( не обязан быть дискретным), то есть на лейбле.

$log P(X|Y;theta_2) - KL[Q(Z|X,Y;theta_1)||P(Z|X,Y;theta_2)]=E_{Z sim Q}[log P(X|Z,Y;theta_2)] - KL[Q(Z|X,Y;theta_1)||N(0,I)]$

Q(Z|X,Y;theta_1) мы опять сравниваем с N(0,I) .
Это можно интерпретировать так: для каждого у нас отдельный автоэнкодер VAE, при этом у них огромное количество общих весов (почти абсолютный weight sharing).

В результате получается, что CVAE кодирует в свойства входного сигнала общие для всех .

Перенос стиля

(Комментарий: это не то же самое, что перенос стиля в Prisme, там совсем другое)

Теперь становится понятно, как создавать новые картинки в стиле заданной:

обучаем CVAE на картинках с лейблами,
кодируем стиль заданной картинки в ,
меняя лейблы , создаем из закодированного новые картинки.

Код на Keras

Код практически идентичен коду из предыдущей части, за исключением того, что теперь в энкодер и декодер передается и лейбл цифры.

Код

import sys
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# import seaborn as sns

from keras.datasets import mnist
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test  = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test  = np.reshape(x_test,  (len(x_test),  28, 28, 1))

y_train_cat = to_categorical(y_train).astype(np.float32)
y_test_cat  = to_categorical(y_test).astype(np.float32)
num_classes = y_test_cat.shape[1]

batch_size = 500
latent_dim = 8
dropout_rate = 0.3
start_lr = 0.001

from keras.layers import Input, Dense 
from keras.layers import BatchNormalization, Dropout, Flatten, Reshape, Lambda
from keras.layers import concatenate
from keras.models import Model
from keras.objectives import binary_crossentropy
from keras.layers.advanced_activations import LeakyReLU
from keras import backend as K


def create_cvae():
    models = {}

    # Добавим Dropout и BatchNormalization
    def apply_bn_and_dropout(x):
        return Dropout(dropout_rate)(BatchNormalization()(x))

    # Энкодер
    input_img = Input(shape=(28, 28, 1))
    flatten_img = Flatten()(input_img)
    input_lbl = Input(shape=(num_classes,), dtype='float32')

    x = concatenate([flatten_img, input_lbl])
    x = Dense(256, activation='relu')(x)
    x = apply_bn_and_dropout(x)
    # Предсказываем параметры распределений
    # Вместо того чтобы предсказывать стандартное отклонение, предсказываем логарифм вариации
    z_mean = Dense(latent_dim)(x)
    z_log_var = Dense(latent_dim)(x)

    # Сэмплирование из Q с трюком репараметризации
    def sampling(args):
        z_mean, z_log_var = args
        epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0)
        return z_mean + K.exp(z_log_var / 2) * epsilon
    l = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])

    models["encoder"]  = Model([input_img, input_lbl], l, 'Encoder') 
    models["z_meaner"] = Model([input_img, input_lbl], z_mean, 'Enc_z_mean')
    models["z_lvarer"] = Model([input_img, input_lbl], z_log_var, 'Enc_z_log_var')

    # Декодер
    z = Input(shape=(latent_dim, ))
    input_lbl_d = Input(shape=(num_classes,), dtype='float32')
    x = concatenate([z, input_lbl_d])
    x = Dense(256)(x)
    x = LeakyReLU()(x)
    x = apply_bn_and_dropout(x)
    x = Dense(28*28, activation='sigmoid')(x)
    decoded = Reshape((28, 28, 1))(x)

    models["decoder"] = Model([z, input_lbl_d], decoded, name='Decoder')
    models["cvae"]    = Model([input_img, input_lbl, input_lbl_d], 
                              models["decoder"]([models["encoder"]([input_img, input_lbl]), input_lbl_d]), 
                              name="CVAE")
    models["style_t"] = Model([input_img, input_lbl, input_lbl_d], 
                               models["decoder"]([models["z_meaner"]([input_img, input_lbl]), input_lbl_d]), 
                               name="style_transfer")
    
    
    def vae_loss(x, decoded):
        x = K.reshape(x, shape=(batch_size, 28*28))
        decoded = K.reshape(decoded, shape=(batch_size, 28*28))
        xent_loss = 28*28*binary_crossentropy(x, decoded)
        kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
        return (xent_loss + kl_loss)/2/28/28

    return models, vae_loss

models, vae_loss = create_cvae()
cvae = models["cvae"]

from keras.optimizers import Adam, RMSprop
cvae.compile(optimizer=Adam(start_lr), loss=vae_loss)

digit_size = 28
def plot_digits(*args, invert_colors=False):
    args = [x.squeeze() for x in args]
    n = min([x.shape[0] for x in args])
    figure = np.zeros((digit_size * len(args), digit_size * n))

    for i in range(n):
        for j in range(len(args)):
            figure[j * digit_size: (j + 1) * digit_size,
                   i * digit_size: (i + 1) * digit_size] = args[j][i].squeeze()

    if invert_colors:
        figure = 1-figure

    plt.figure(figsize=(2*n, 2*len(args)))
    plt.imshow(figure, cmap='Greys_r')
    plt.grid(False)
    ax = plt.gca()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    plt.show()


n = 15 # Картинка с 15x15 цифр

from scipy.stats import norm
# Так как сэмплируем из N(0, I), то сетку узлов, в которых генерируем цифры, берем из обратной функции распределения
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))

def draw_manifold(generator, lbl, show=True):
    # Рисование цифр из многообразия
    figure = np.zeros((digit_size * n, digit_size * n))
    input_lbl = np.zeros((1, 10))
    input_lbl[0, lbl] = 1
    for i, yi in enumerate(grid_x):
        for j, xi in enumerate(grid_y):
            z_sample = np.zeros((1, latent_dim))
            z_sample[:, :2] = np.array([[xi, yi]])

            x_decoded = generator.predict([z_sample, input_lbl])
            digit = x_decoded[0].squeeze()
            figure[i * digit_size: (i + 1) * digit_size,
                   j * digit_size: (j + 1) * digit_size] = digit
    if show:
        # Визуализация
        plt.figure(figsize=(10, 10))
        plt.imshow(figure, cmap='Greys_r')
        plt.grid(False)
        ax = plt.gca()
        ax.get_xaxis().set_visible(False)
        ax.get_yaxis().set_visible(False)
        plt.show()
    return figure


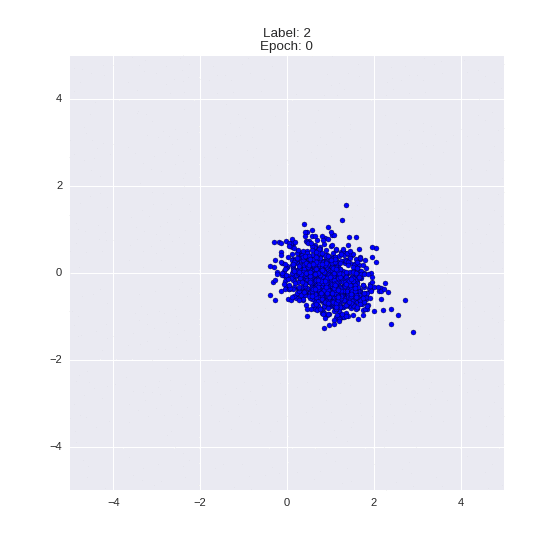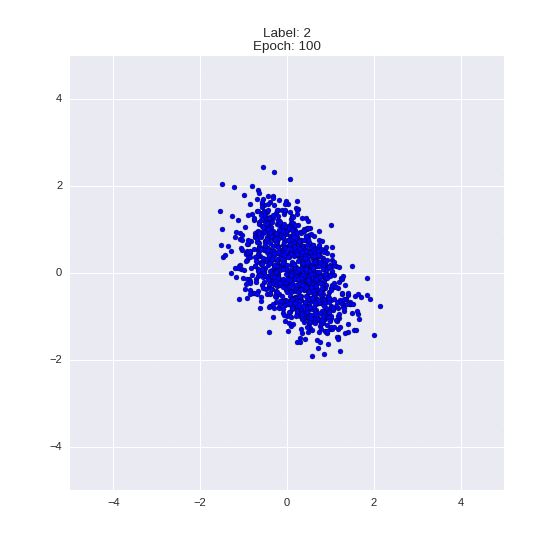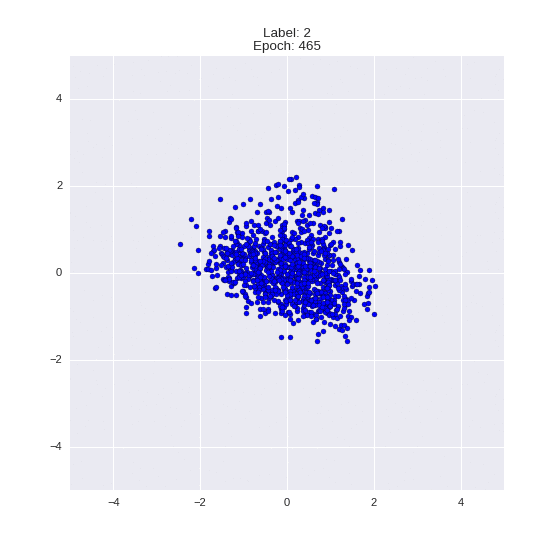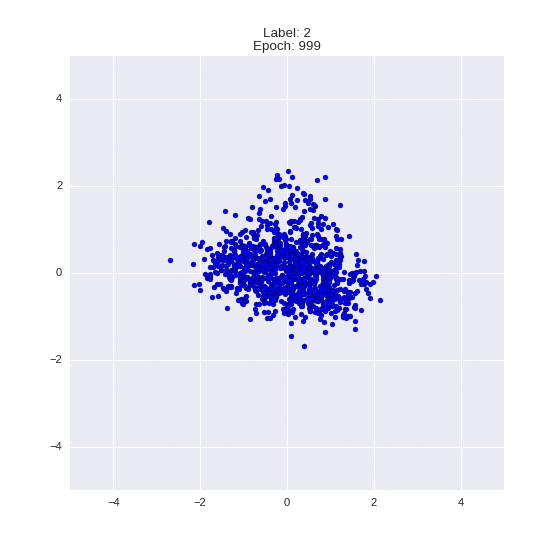
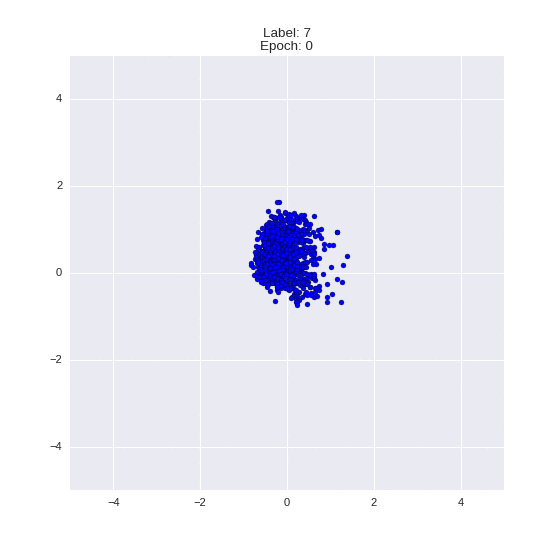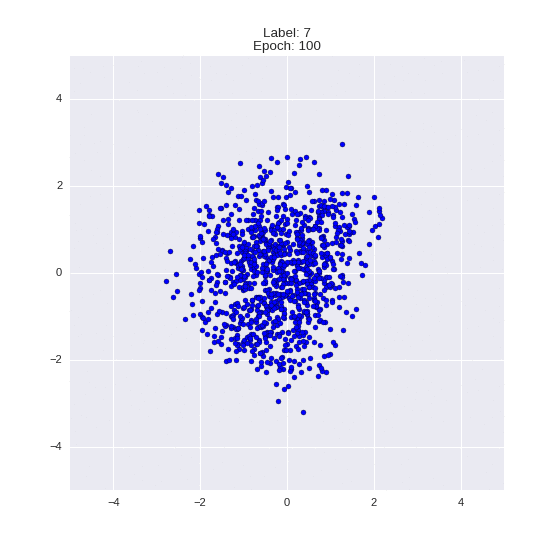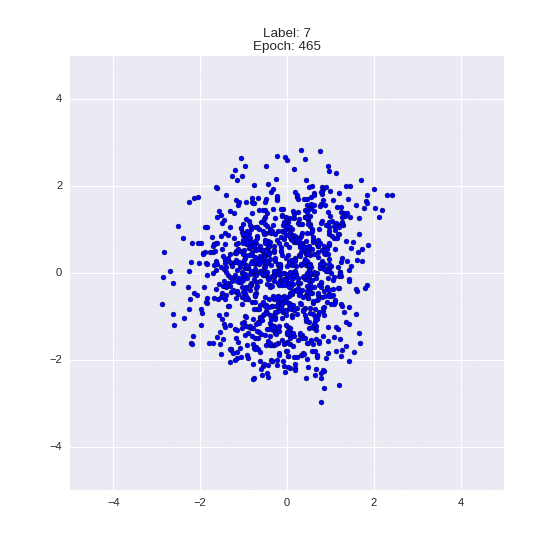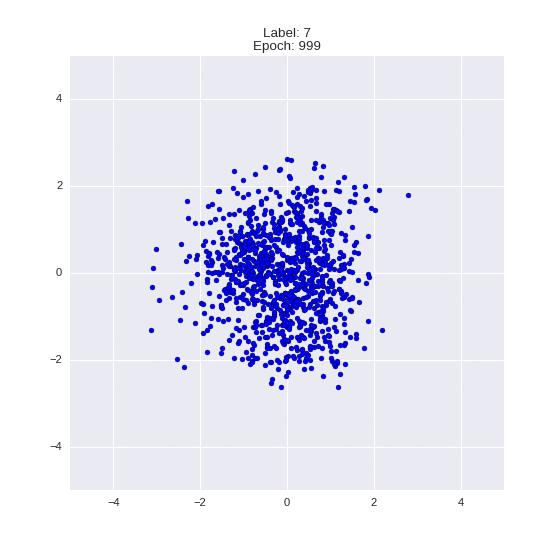
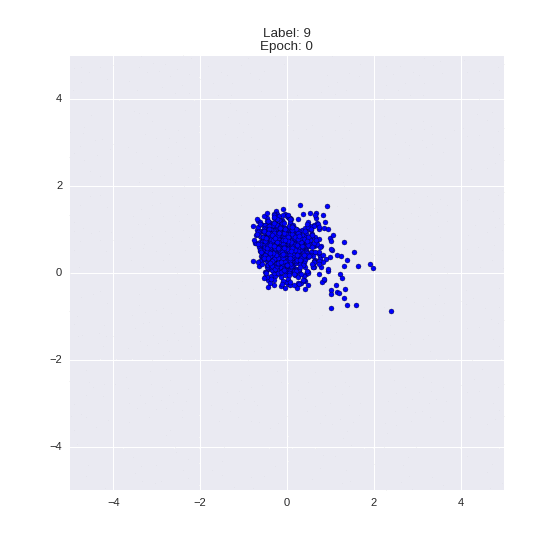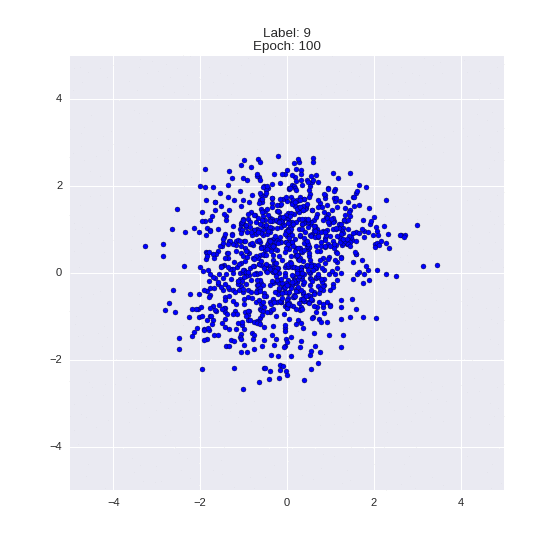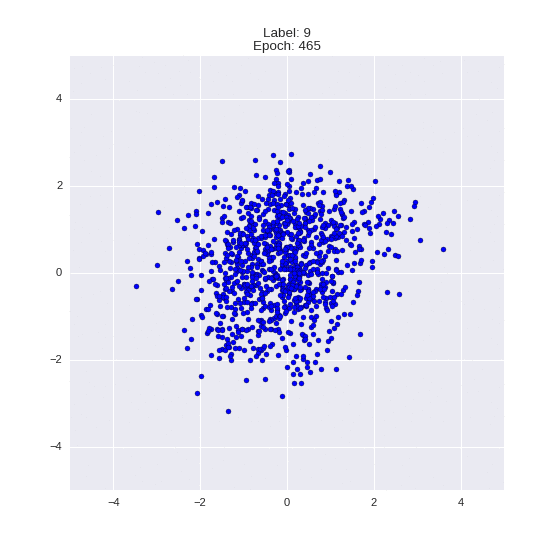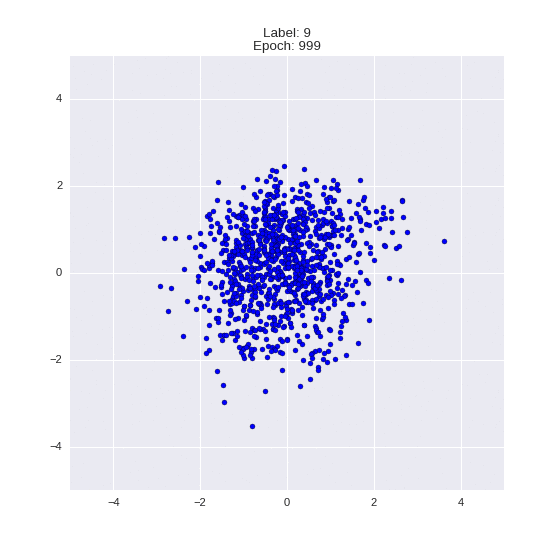
def draw_z_distr(z_predicted, lbl):
    # Рисование рпспределения z
    input_lbl = np.zeros((1, 10))
    input_lbl[0, lbl] = 1
    im = plt.scatter(z_predicted[:, 0], z_predicted[:, 1])
    im.axes.set_xlim(-5, 5)
    im.axes.set_ylim(-5, 5)
    plt.show()

from IPython.display import clear_output
from keras.callbacks import LambdaCallback, ReduceLROnPlateau, TensorBoard

# Массивы, в которые будем сохранять результаты для последующей визуализации
figs = [[] for x in range(num_classes)]
latent_distrs = [[] for x in range(num_classes)]
epochs = []

# Эпохи, в которые будем сохранять
save_epochs = set(list((np.arange(0, 59)**1.701).astype(np.int)) + list(range(10)))

# Отслеживать будем на вот этих цифрах
imgs = x_test[:batch_size]
imgs_lbls = y_test_cat[:batch_size]
n_compare = 10

# Модели
generator      = models["decoder"]
encoder_mean   = models["z_meaner"]


# Функция, которую будем запускать после каждой эпохи
def on_epoch_end(epoch, logs):
    if epoch in save_epochs:
        clear_output() # Не захламляем output

        # Сравнение реальных и декодированных цифр
        decoded = cvae.predict([imgs, imgs_lbls, imgs_lbls], batch_size=batch_size)
        plot_digits(imgs[:n_compare], decoded[:n_compare])

        # Рисование многообразия для рандомного y и распределения z|y
        draw_lbl = np.random.randint(0, num_classes)
        print(draw_lbl)
        for lbl in range(num_classes):
            figs[lbl].append(draw_manifold(generator, lbl, show=lbl==draw_lbl))
            idxs = y_test == lbl
            z_predicted = encoder_mean.predict([x_test[idxs], y_test_cat[idxs]], batch_size)
            latent_distrs[lbl].append(z_predicted)
            if lbl==draw_lbl:
                draw_z_distr(z_predicted, lbl)
        epochs.append(epoch)


# Коллбэки
pltfig = LambdaCallback(on_epoch_end=on_epoch_end)
# lr_red = ReduceLROnPlateau(factor=0.1, patience=25)
tb     = TensorBoard(log_dir='./logs')


# Запуск обучения 
cvae.fit([x_train, y_train_cat, y_train_cat], x_train, shuffle=True, epochs=1000,
         batch_size=batch_size,
         validation_data=([x_test, y_test_cat, y_test_cat], x_test),
         callbacks=[pltfig, tb],
         verbose=1)

Результаты

(Извиняюсь, что местами белые цифры на черном фоне, а местами черные на белом)

Переводит цифры этот автоэнкодер вот так:
Автоэнкодеры в Keras, Часть 4: Conditional VAE - 18

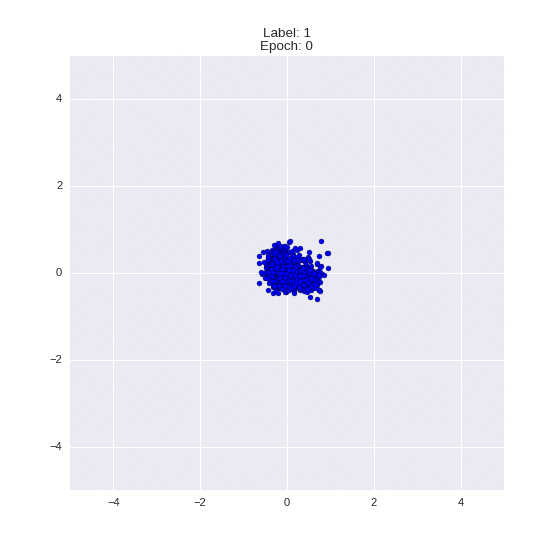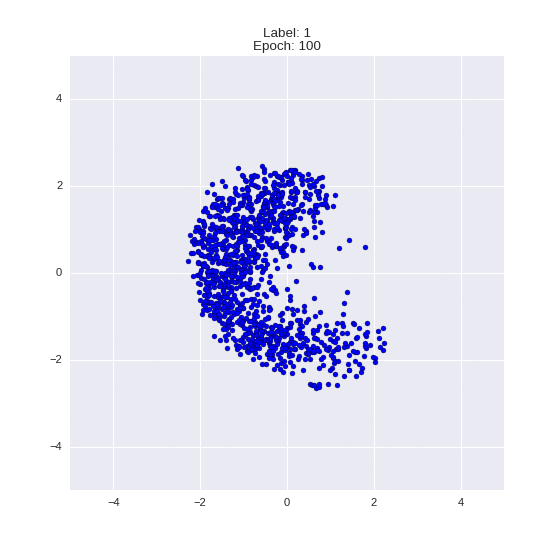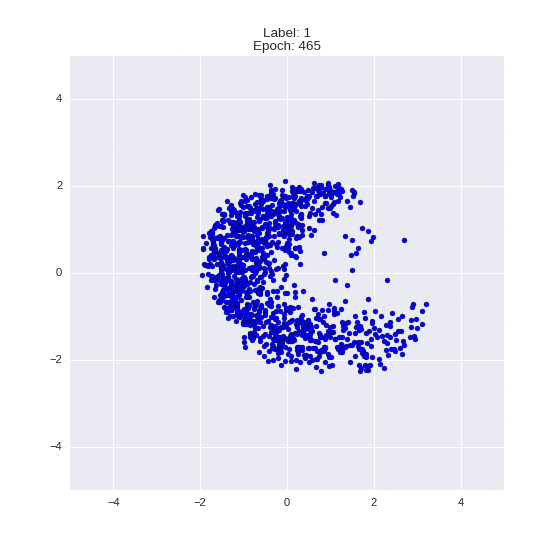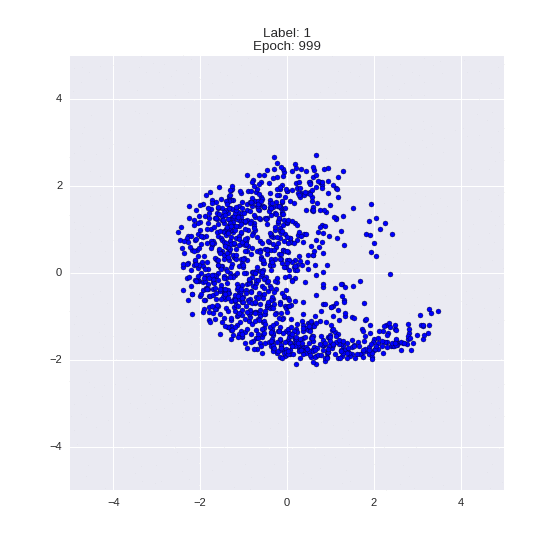
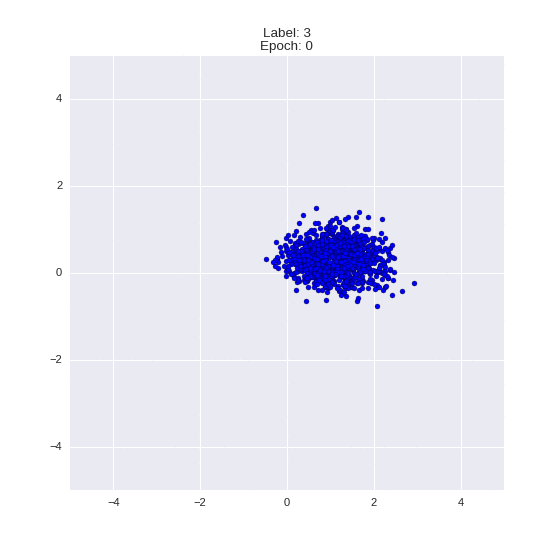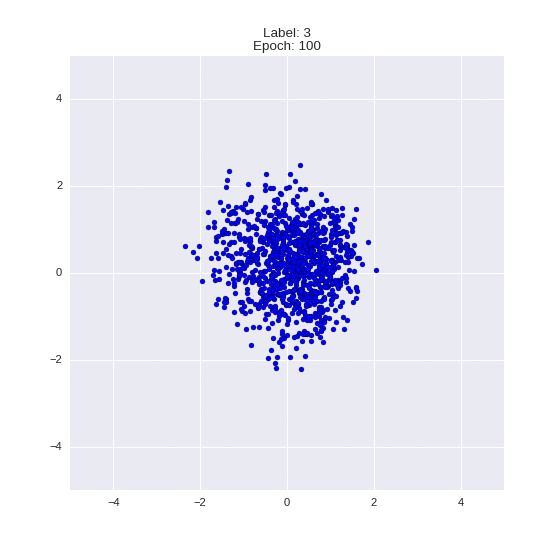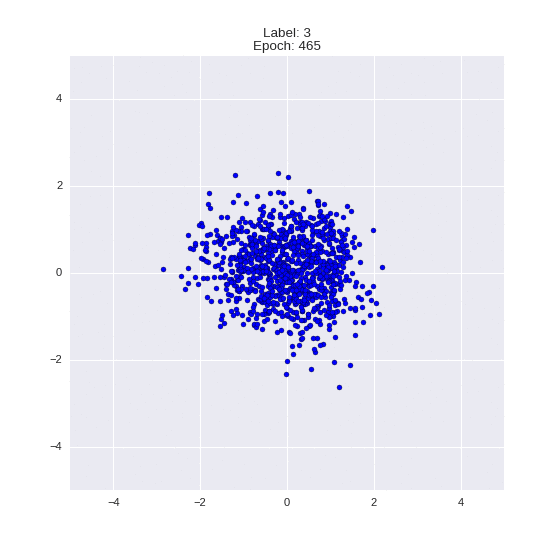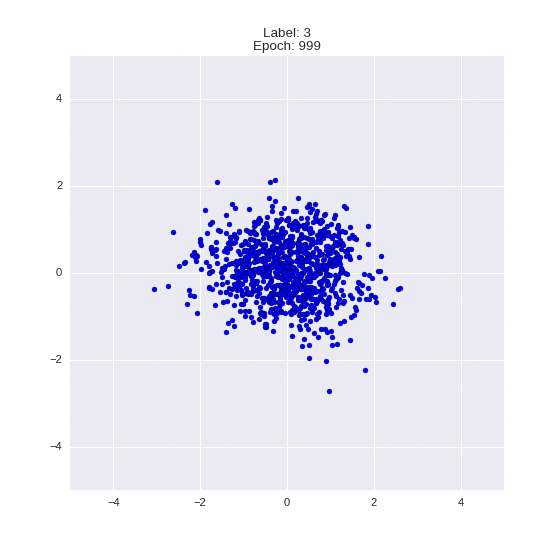
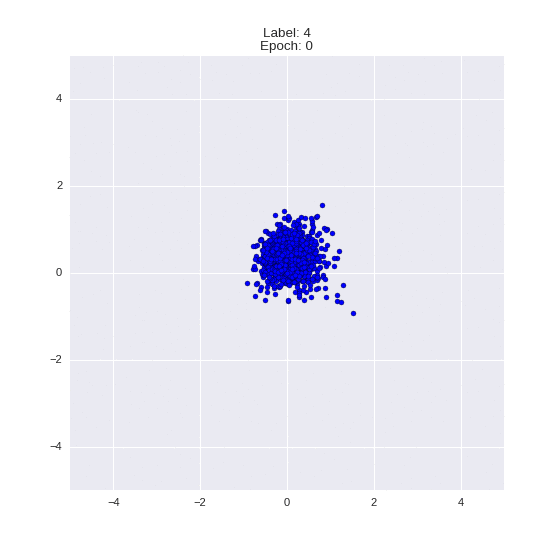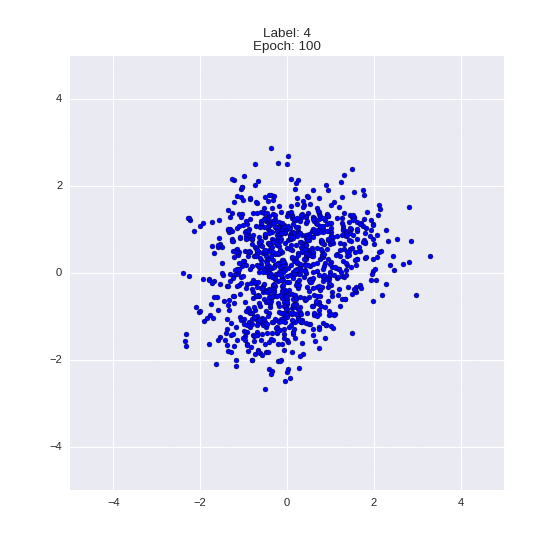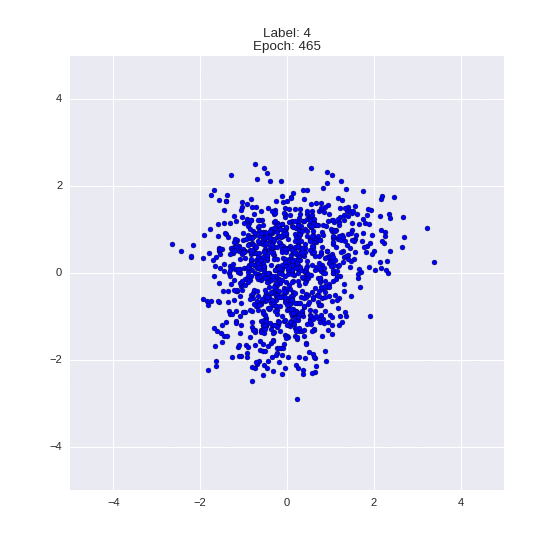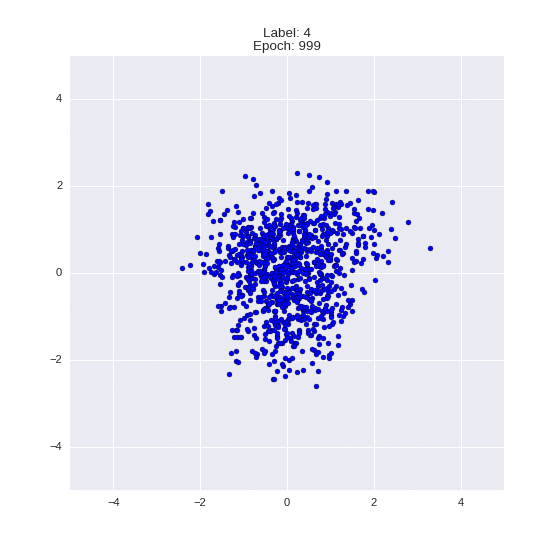
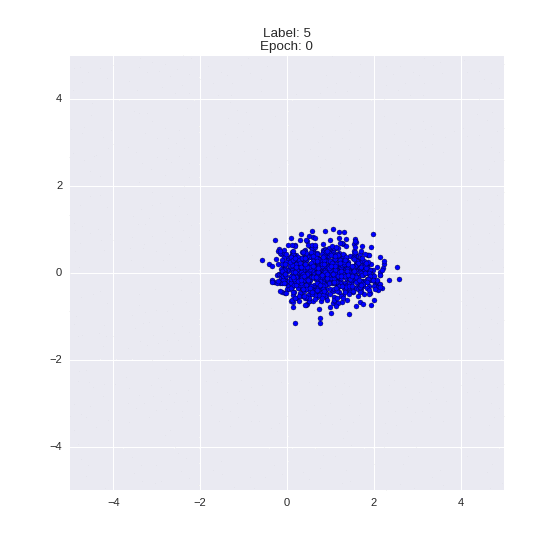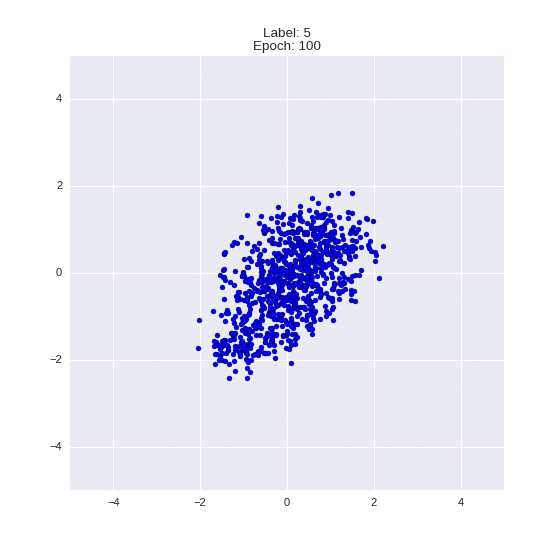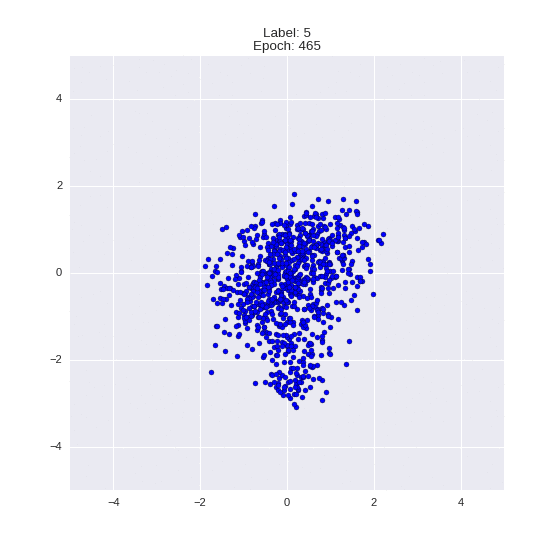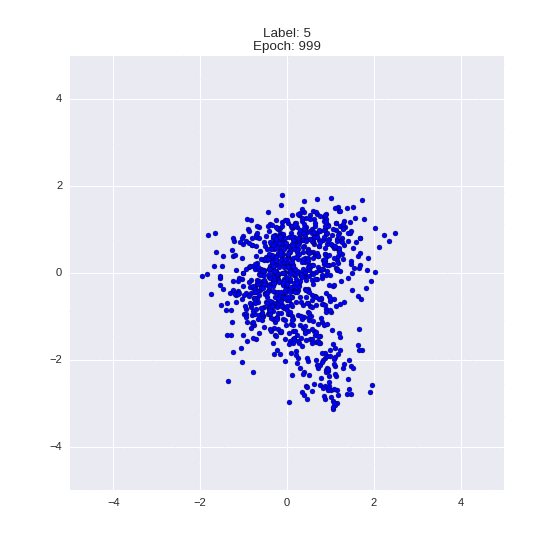
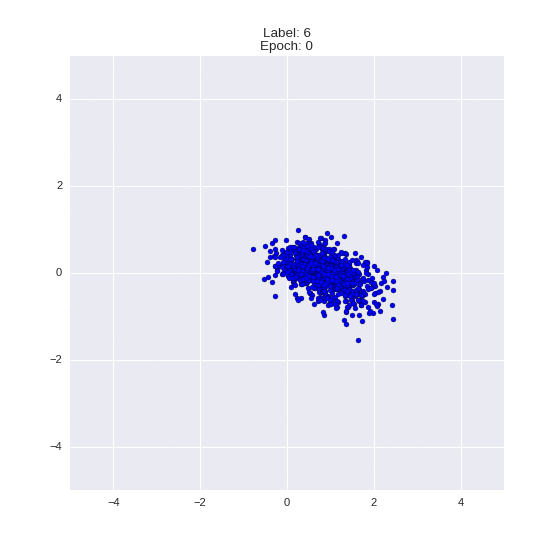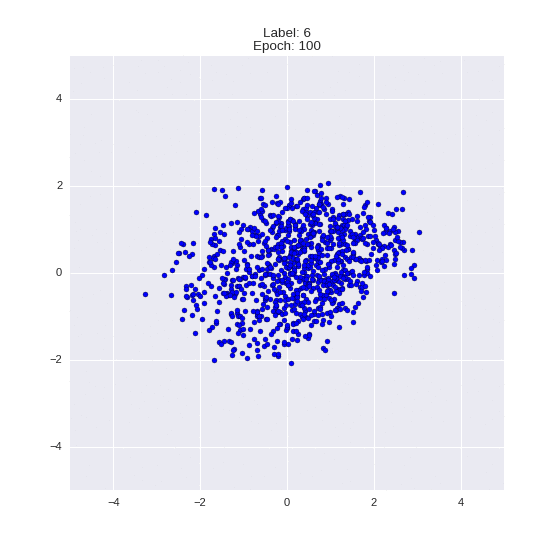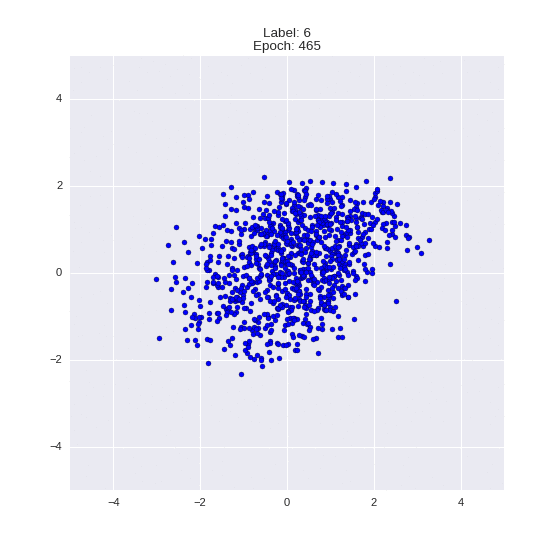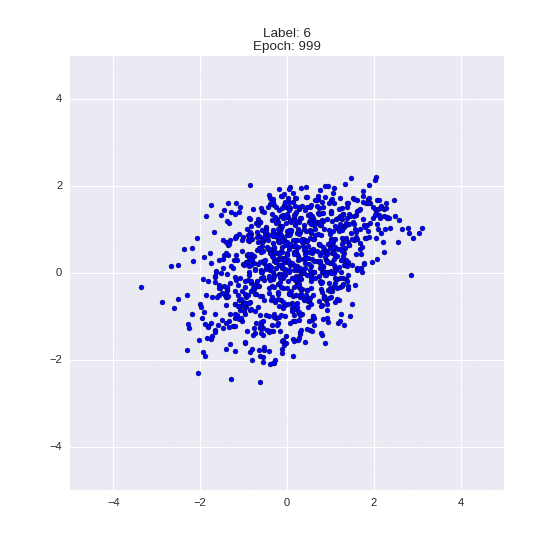
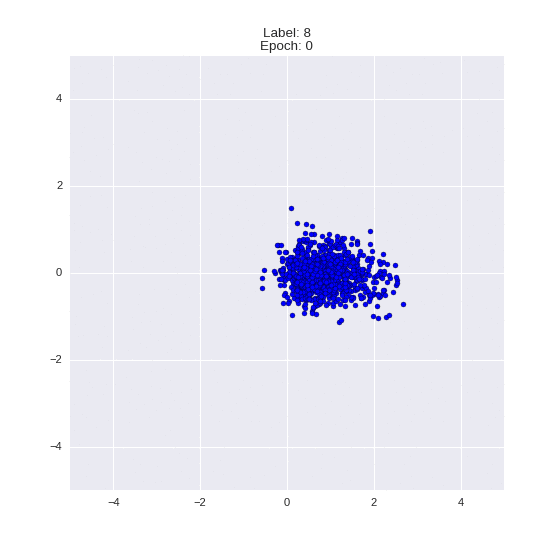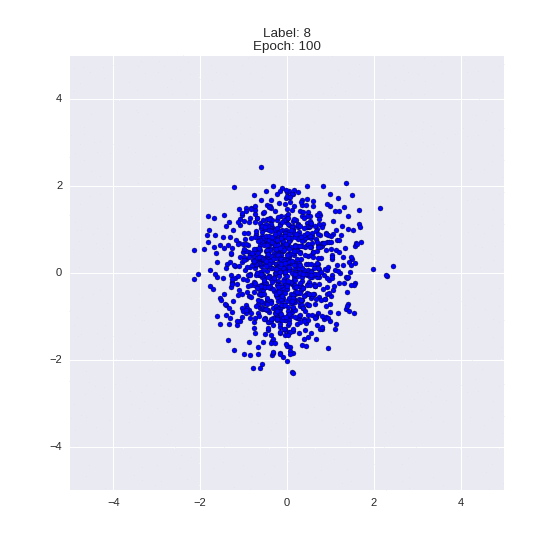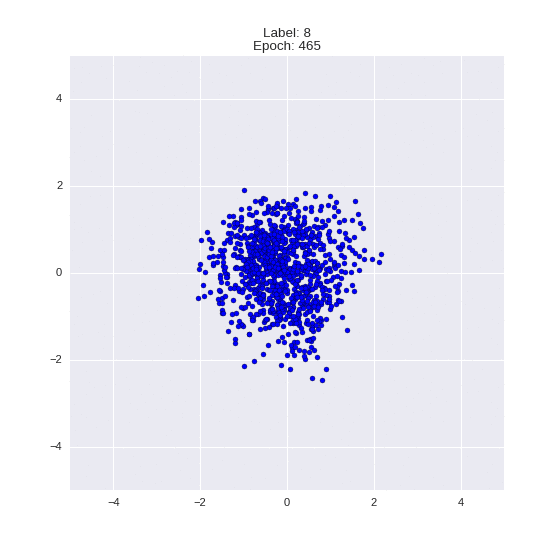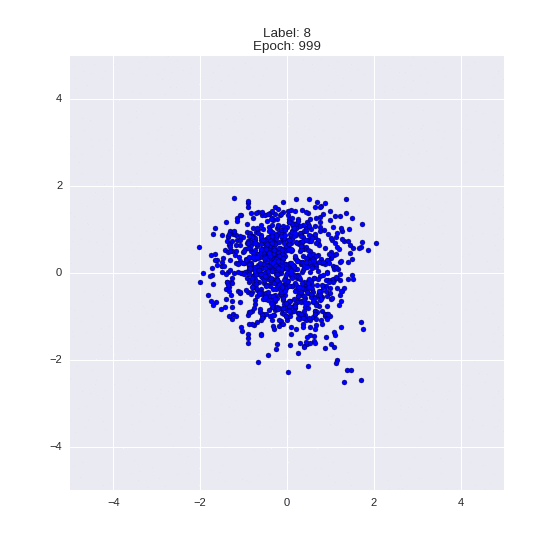
Сгенерированные цифры каждого лейбла сэмплированные из N(0|I) :

(Отлично видно как общие черты закодированы в координатах )

Генерация цифр заданного лейбла из и распределение для каждого лейбла

Тяжелые гифки

Автоэнкодеры в Keras, Часть 4: Conditional VAE - 33

Автоэнкодеры в Keras, Часть 4: Conditional VAE - 34

Перенос стиля этой моделью

В качестве источников стиля возьмем первые десять «7»-ок, и на основе их кода создадим остальные цифры.

Код

def style_transfer(model, X, lbl_in, lbl_out):
    rows = X.shape[0]
    if isinstance(lbl_in, int):
        lbl = lbl_in
        lbl_in = np.zeros((rows, 10))
        lbl_in[:, lbl] = 1
    if isinstance(lbl_out, int):
        lbl = lbl_out
        lbl_out = np.zeros((rows, 10))
        lbl_out[:, lbl] = 1
    return model.predict([X, lbl_in, lbl_out])

n = 10
lbl = 7
generated = []
prot = x_train[y_train == lbl][:n]

for i in range(num_classes):
    generated.append(style_transfer(models["style_t"], prot, lbl, i))

generated[lbl] = prot
plot_digits(*generated, invert_colors=True)

Автоэнкодеры в Keras, Часть 4: Conditional VAE - 52

Стиль перенесен довольно удачно: сохранены наклон и толщина штриха.

Больше свойств стиля можно было бы переносить, просто увеличив размерность , это также сделало бы цифры менее размытыми.

В следующей части посмотрим, как, используя генеративные состязающиеся сети (GAN), генерировать цифры практически неотличимые от настоящих, а после этого и как объединить GAN'ы с автоэнкодерами.

Код создания гифок

Код

from matplotlib.animation import FuncAnimation
from matplotlib import cm
import matplotlib

def make_2d_figs_gif(figs, epochs, c, fname, fig): 
    norm = matplotlib.colors.Normalize(vmin=0, vmax=1, clip=False)
    im = plt.imshow(np.zeros((28,28)), cmap='Greys', norm=norm)
    plt.grid(None)
    plt.title("Label: {}nEpoch: {}".format(c, epochs[0]))

    def update(i):
        im.set_array(figs[i])
        im.axes.set_title("Label: {}nEpoch: {}".format(c, epochs[i]))
        im.axes.get_xaxis().set_visible(False)
        im.axes.get_yaxis().set_visible(False)
        return im
    
    anim = FuncAnimation(fig, update, frames=range(len(figs)), interval=100)
    anim.save(fname, dpi=80, writer='imagemagick')

def make_2d_scatter_gif(zs, epochs, c, fname, fig):
    im = plt.scatter(zs[0][:, 0], zs[0][:, 1])
    plt.title("Label: {}nEpoch: {}".format(c, epochs[0]))

    def update(i):
        fig.clear()
        im = plt.scatter(zs[i][:, 0], zs[i][:, 1])
        im.axes.set_title("Label: {}nEpoch: {}".format(c, epochs[i]))
        im.axes.set_xlim(-5, 5)
        im.axes.set_ylim(-5, 5)
        return im

    anim = FuncAnimation(fig, update, frames=range(len(zs)), interval=100)
    anim.save(fname, dpi=80, writer='imagemagick')

for lbl in range(num_classes):
    make_2d_figs_gif(figs[lbl], epochs, lbl, "./figs4/manifold_{}.gif".format(lbl), plt.figure(figsize=(7,7)))
    make_2d_scatter_gif(latent_distrs[lbl], epochs, lbl, "./figs4/z_distr_{}.gif".format(lbl), plt.figure(figsize=(7,7)))

Полезные ссылки и литература

Теоретическая часть основана на статье:
[1] Tutorial on Variational Autoencoders, Carl Doersch, https://arxiv.org/abs/1606.05908
и фактически является ее кратким изложением.

Многие картинки взяты из блога Isaac Dykeman:
[2] Isaac Dykeman, http://ijdykeman.github.io/ml/2016/12/21/cvae.html

Подробнее прочитать про расстояние Кульбака-Лейблера на русском можно в
[3] http://www.machinelearning.ru/wiki/images/d/d0/BMMO11_6.pdf

Код частично основан на статье Francois Chollet:
[4] https://blog.keras.io/building-autoencoders-in-keras.html

Другие интересные ссылки:
http://blog.fastforwardlabs.com/2016/08/12/introducing-variational-autoencoders-in-prose-and.html
http://kvfrans.com/variational-autoencoders-explained/

Автор: iphysic

Источник

Информация

Обсуждаемое

Рекомендуем

Автоэнкодеры в Keras, Часть 4: Conditional VAE

Содержание

Сначала подумаем о причинах 1-го недостатка:

CVAE

Перенос стиля

Код на Keras

Результаты

Генерация цифр заданного лейбла из и распределение для каждого лейбла

Перенос стиля этой моделью

Код создания гифок

Полезные ссылки и литература

Архив

Информация

Обсуждаемое

Рекомендуем

Автоэнкодеры в Keras, Часть 4: Conditional VAE

Содержание

Сначала подумаем о причинах 1-го недостатка:

CVAE

Перенос стиля

Код на Keras

Результаты

Генерация цифр заданного лейбла из и распределение для каждого лейбла

Перенос стиля этой моделью

Код создания гифок

Полезные ссылки и литература

Рекомендованный контент

Новости

Актуальные темы

Архив