Задача
Задача звучит просто – напечатать таблицу. Напечатать так, чтобы она выглядела красиво и, по возможности, не расползалась.
После некоторых раздумий, решено было воспользоваться FOP для генерации PDF. Загвоздка в том, что Apache FOP не поддерживает table-layout:auto, то есть при построении таблицы необходимо вручную задать ширину столбцов (хорошо еще, что можно задать относительную ширину в процентах). Если же сделать все столбцы одинаковой ширины, таблица будет выглядеть несколько неэлегантно. Выходит, рассчитывать ширину придется вручную.
Основная идея в том, что ширину столбцов необходимо подобрать таким образом, чтобы как можно сильнее сократить число переносов строк внутри ячеек таблицы.
Решение
Я решал задачу на С++ с использованием фреймворка Qt, поэтому некоторые отсылки к языку и Qt определенно будут, но в общем-то, я постараюсь избежать кода и описать основную идею решения.
Подготовка данных
Во-первых, определимся, какие данные потребуются. Текст в каждой ячейке таблицы разобьем на слова, для каждого слова вычислим, сколько места на бумаге оно занимает. Таким образом, для каждой ячейки будем хранить массив длин слов ее текста.
Кроме того, необходимо знать ширину бумаги, причем выраженную в тех же единицах, что и длина слов.
Я использовал QFontMetrics::width для определения длины слов. Таким образом, длина слов получалась в пикселах. Тогда для того, чтобы определить ширину бумаги в пикселах, достаточно перемножить ее ширину в дюймах на DPI экрана, которое можно получить, воспользовавшись функцией QPaintDevice::logicalDpiX.
Может оказаться, что ширина бумаги недостаточна для того, чтобы вместить таблицу, даже если сжать столбцы настолько, что в каждой строке будет умещаться всего по одному слову.
Вероятность такого варианта развития событий мала (если Вы не немец и не тестировщик, конечно), поэтому я не стал разрабатывать сколько-нибудь сложный алгоритм обработки такого рода случаев. Просто проверим, что минимальная ширина таблицы, которая определяется как сумма максимальных длин слов в столбцах, меньше размера бумаги.
| минимальная ширина таблицы |
определяется суммой длин самых длинных слов в столбцах |
Если таблица не влезает, придется обрезать длинные слова. Поскольку, раз уж слово решили обрезать, то обрезать его можно в любом месте, будем считать эффективную длину таких обрезанных слов равной нулю.
Итак, будем обрезать самое длинное слово в таблице до тех пор, пока таблица не станет вмещаться на бумагу.
На этом подготовку данных можно считать законченной, и можно перейти к алгоритму расчета ширины столбцов.
Расчет
В начале статьи я определил основную идею решения. Теперь настало время выразить ее более формально. Фактически, необходимо отобразить таблицу на бумаге таким образом, чтобы как можно сильнее сократить площадь таблицы.
Площадь, занимаемую таблицей, можно определить как сумму площадей ее столбцов:

Здесь  и
и  – высота и ширина столбца соответственно.
– высота и ширина столбца соответственно.
Конечно, это не совсем верно, но такая модель на практике дает вполне удовлетворительный результат.
Распишем, чему равна высота столбца:

где m – число строк таблицы, lh – высота строки текста, p – некоторый коэффициент, описывающий высоту отступов, wc – число переносов строк.
Поскольку на число строк, высоту строки и отступы влиять невозможно, то их можно вынести в отдельный коэффициент A.
А вот количество переносов строк напрямую зависит от ширины столбца. Таким образом, высоту столбца можно переписать в виде:

А задача сводится к минимизации функции

Да-да, я не ошибся, А и B не будут зависеть от k, поскольку B определяется высотой строки, а A, в добавок, размерами отступов и числом строк.
S можно переписать в виде:

Сейчас я сделаю большую грубость.  – это идеальная площадь таблицы, когда переносов вообще нет. Но поскольку нас не интересует оптимизация по ширине таблицы, (в итоге все равно растянем таблицу на всю страницу), то заменим
– это идеальная площадь таблицы, когда переносов вообще нет. Но поскольку нас не интересует оптимизация по ширине таблицы, (в итоге все равно растянем таблицу на всю страницу), то заменим  , то есть на постоянную. Теперь все просто: для задачи минимизации коэффициенты G и B никакой роли не играют, поэтому их можно благополучно выкинуть и находить минимум функции
, то есть на постоянную. Теперь все просто: для задачи минимизации коэффициенты G и B никакой роли не играют, поэтому их можно благополучно выкинуть и находить минимум функции

Для нахождения минимума функции возьмем за основу метод градиентного спуска, но будем спускаться не в направлении градиента, а по той координате, изменение функции (частная производная, помноженная на изменение координаты) по которой имеет наименьшее (оно же наибольшее по модулю) значение.
Вы сказали производная?
На самом деле, функция числа переносов в зависимости от ширины столба не отличается особой гладкостью. Это ступенчатая функция, которая терпит разрывы в точках изменения числа переносов. Выглядит это как-то так:
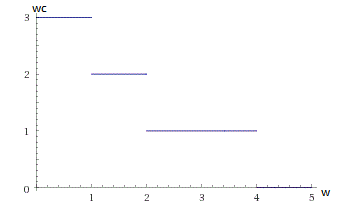
У такой функции явные проблемы с производными, но мы поступим просто: будем рассматривать не саму функцию, а некоторую монотонно-убывающую функцию, которая в точках изменения числа переносов совпадает с правым пределом изначальной функции.
В качестве начальной точки возьмем точку с наименьшими возможными ширинами столбцов.
Алгоритм
Для каждого столбца:
- Построим массивы точек, в которых число переносов в данном столбце изменяется – mk.
- Массивы значений гладкой функции числа переносов в этих точках (гладкую функцию я определил в предыдущем пункте) – wck.
Для того, чтобы сформировать эти массивы, используем подготовленные на первом этапе данные о длине слов в каждой ячейке таблицы.
Дополним массивы (их получилось столько же, сколько и столбцов) начальными точками.
В итоге, для столбца
| минимальная ширина таблицы |
получим следующую структуру данных:
| m0 | wc0 |
| 11 | 2 |
| 13 («ширина» и «таблицы» — на одной строке) | 1 |
| 24 | 0 |
Аналогичные структуры получим и для остальных столбцов.
Теперь запустим итерационный процесс:
Пока сумма ширин столбцов меньше чем ширина страницы:
- Вычислим изменение функции площади (U) при движении по каждой координате по формуле

(Это хорошо всем известная формула взятия дифференциала произведения: d(AB) = B dA + A dB) - Если в каком-то массиве остался всего один элемент, значит в данном столбце уже нет переносов строк (wck[0] == 0). Такой столбец мы не берем в рассмотрение.
- Если ни один массив не попал в рассмотрение, во всех столбцах уже отсутствуют переносы строк, заканчиваем вычисления.
- Увеличиваем ширину k-го столбца, в котором величина dk — наибольшая. Удаляем первые элементы массивов wck и mk для этого столбца.
В заключение, пересчитаем полученные ширины столбцов из абсолютных единиц в проценты. Тем самым, отвяжемся от той метрики шрифта, которую использовали.
Итог
В итоге таблица получается именно такой, какой бы я ее сделал при ручном форматировании.
P.S.
Статья не претендует на математическую строгость, зато показывает, где вам может пригодиться немного математики в прикладном программировании.
Автор: Lol4t0



