Одно из самых неинтуитивных следствий теории относительности Эйнштейна состоит в том, что не существует абсолютного пространства или абсолютного времени. Если спросить вас, где и когда вы находитесь, вы ответите. Но если мы с вами разойдёмся на большое расстояние, и я спрошу вас, где и когда, как вам кажется, нахожусь я, то наши с вами ответы не обязательно совпадут. Оказывается, в общей теории относительности не существует универсального метода определения пространства и времени (и расстояний) кроме того места, где находитесь вы. В результате у нас есть множество способов определять такие вещи, и именно с этим связан вопрос читателя:
Я хотел бы увидеть ваше объяснение конформного времени и сопутствующего расстояния – что это такое, когда и как их используют по сравнению с привычными временем и расстоянием.
Используя в обычной речи такие понятия, как «время» и «расстояние», мы делаем множество предположений, о которых очень редко задумываемся.

Если вы считаете, что вы можете сообщить мне, что там, где нахожусь я, время дня равняется 10:05 утра, а нахожусь я от вас на расстоянии в 700 метров, вы можете не понимать, на каком основании вы уверены в своих оценках. Вы предполагаете, что наши с вами часы идут с одинаковой скоростью, что они происходят из одного места, в котором мы с вами согласовали значение времени, и что когда мы вновь сведём эти часы вместе, они также будут согласовываться друг с другом. Всё просто, не правда ли?
Но это возможно, только если выполняются два важных условия:
1. Ничего не двигается по отношению ко всему остальному. Если два объекта приобретают скорость друг относительно друга, они испытывают течение времени (и ощущение расстояния) по-разному. Нестабильные частицы, движущиеся со скоростями, близкими к скорости света, кажутся нам живущими дольше из-за растяжения времени, а космонавты на борту МКС, быстро двигающиеся вокруг Земли, стареют немного не так, как люди, находящиеся неподвижно на Земле.
2. Пространство абсолютно плоское, чего никогда не бывает. Во Вселенной работает ОТО, а согласно ей существование материи и энергии означает, что пространство искривлено, и что часы идут с разными скоростями в зависимости от глубины погружения в гравитационное поле. Часы на верхушке Эмпайр-стейт-билдинг каждый год отстают на несколько микросекунд от часов у её подножия.
Те же ограничения действуют и для расстояний: движение и кривизна пространства делают невозможным для наблюдателей в разных местах принять универсальный стандарт расстояний. Но для действительно больших расстояний начинает играть роль ещё кое-что: факт расширения самой ткани пространства Вселенной на космических масштабах. Мы уже не можем говорить о расстояниях между галактиками как о том, что можно измерить некоей согласованной линейкой, поскольку пространство между галактиками со временем расширяется. И это приводит к проблемам, когда мы начинаем говорить, к примеру, о самых отдалённых галактиках во Вселенной.
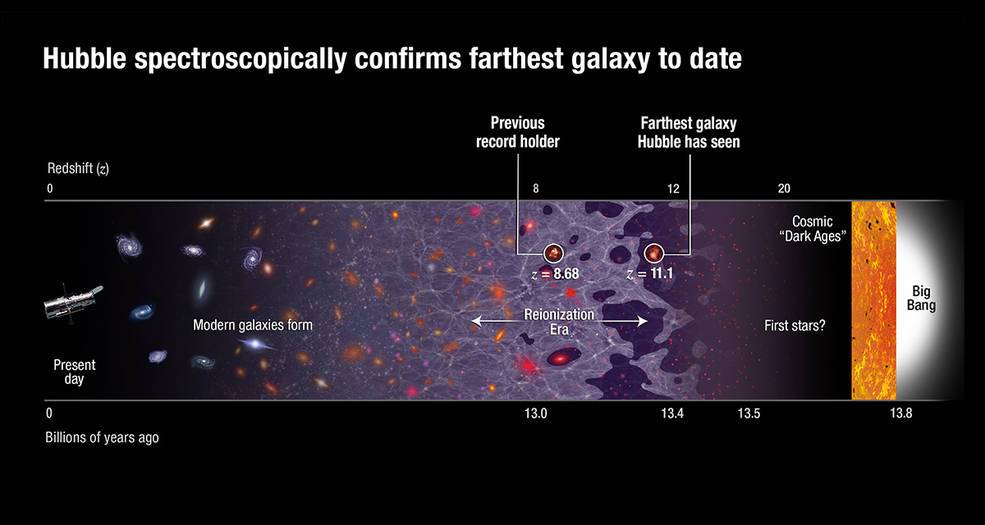
Текущий космический рекордсмен по расстояниям расположен на красном смещении в 11,1 что означает, что за время существования Вселенной, 13,8 млрд лет с Большого взрыва, его свет дошёл до нас, побыв в пути 13,4 млрд лет. Но как далеко от нас эта галактика? Вы могли бы на основе времени, затраченного на путь, решить, что она находится на расстоянии в 13,4 млрд световых лет – но это вряд ли так. Когда свет, дошедший до нас, был испущен этой галактикой, она находилась не более, чем в двух млрд световых лет от нас. Благодаря расширению Вселенной мы, используя общепринятый стандарт измерений, можем сказать, что сейчас она находится в 32 млрд световых лет от нас. Универсальный стандарт расстояний тяжело определить в расширяющейся Вселенной, в которой расстояния меняются со временем.

Так что одно из вводимых нами понятий при ответе на вопрос читателя – концепция разных типов расстояний. Он спрашивает нас об одном из них – о сопутствующем расстоянии. Это одно из моих любимых понятий: оно подразумевает, что расстояния во Вселенной изменяются из-за Хаббловского расширения, поэтому оно исключает расширение из вычислений. Это очень удобно для проведения симуляций формирования таких структур Вселенной, как звёзды, галактики, скопления и нити. Гравитация, конечно, вносит свою лепту, но и Вселенная всё это время расширяется. Зная, как сделать поправку расстояний на расширение, мы можем увидеть, как эволюционируют крупномасштабные структуры Вселенной. Визуально за этим наблюдать гораздо интереснее, чем следить за расширением Вселенной и пытаться различить во всём этом процесс формирования структур.
Поскольку пространство и время неразрывно связаны в объединяющую их концепцию пространства-времени, нам необходимо новое понятие о времени, соответствующее каждому из новых понятий расстояний, которые мы изобретём. Временным партнёром сопутствующего расстояния и будет конформное время. Если бы мы могли волшебным образом мгновенно заморозить всё расширение Вселенной во всех местах, то конформное время соответствует тому, сколько световому лучу потребуется времени на путь из некоего места до вас.
Для наиболее удалённой от нас галактики во Вселенной конформное время составит 32 млрд лет. Для воспринимаемого расстояния от Большого взрыва оно составит 46 млрд лет. И это несмотря на то, что от Большого взрыва до испускания света первой галактикой прошло 400 млн лет. На ранних этапах расширение Вселенной было таким быстрым – и результат этого ощущается и сегодня – что разница в 14 млрд лет конформного времени соответствует разнице в 400 млн лет «правильного» времени (того, которое мы называем просто «время»).
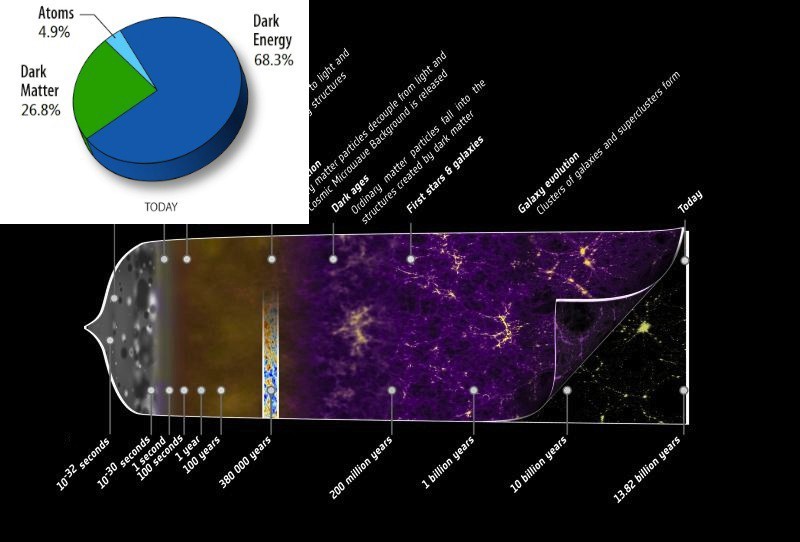
Если рассуждать о событиях, происходящих на Земле, где ничего не движется со скоростями, близкими к световой и не меняется слишком сильно в гравитационном поле, то различные типы «расстояний» и «времён» будут совпадать. Но если говорить о расширяющейся Вселенной на космических масштабах, то правильное расстояние и правильное время могут быть не такими полезными и интересными, как сопутствующее расстояние и конформное время. И в следующий раз, когда вы увидите симуляцию Вселенной и увидите, что Вселенная не выглядит расширяющейся, имейте в виду, что симуляция проходит с использованием сопутствующих расстояний, хотя и может использовать правильное время.
А когда вы услышите что-нибудь об очень удалённом объекте, находящемся от нас на расстоянии меньшем, чем 14 млрд световых лет, имейте в виду, что, скорее всего, речь идёт о сопутствующем расстоянии. Согласно нашим обычным, правильным линейкам, это расстояние, скорее всего, будет гораздо большим!
Автор: SLY_G






