Всем привет. Продолжаем собирать автомобильный автопилот на компьютерном зрении из гитхаба и палок (начало здесь). Сегодня подключаем к делу датчики движения смартфона (акселерометр, гироскоп и GPS приемник) на Android, осваиваем несложный sensor fusion и окончательно закрываем с кодом для сбора обучающей выборки. Бонусы — Android приложение для записи всех сенсоров синхронзированных с видео и больше часа размеченных данных в рамках импортозамещения иностранных конкурсов. Весь код по-прежнему на github.

Это трехосные MEMS акселерометр и гироскоп, они будут нам крайне полезны.
В двух словах напомню (за деталями добро пожаловать в предыдущий пост, что конечная цель — обучить систему, которая по кадрам видео с лобового стекла сможет выдавать управляющие воздействия для автомобиля (угол поворота руля и желаемую скорость или ускорение). Для этого нужна обучающая выборка — видео с заездов, где машиной управляет человек, и синхронизированная по времени информация об угле поворота и скорости. В современных автомобилях эти данные можно считывать через CAN шину, но надо во-первых покупать и подключать специальный CAN адаптер, а во-вторых разбираться с расшифровкой протокола и формата данных, которые у разных производителей разные. Вместо всей этой возни мы вычисляем управляющие воздействия косвенно — из сырых данных с обычного смартфона, ни к чему дополнительно не подключенного.
В прошлой серии мы научились определять угловую скорость поворота автомобиля в горизонтальной плоскости на основе только видео кадров с помощью библиотеки видео-SLAM. К сожалению, на практике эта библиотека очень неточно вычисляет поступательную скорость устройства. А не зная поступательную скорость, мы не можем обучить даже компонент поворота руля для автопилота по отдельности, так как угловая скорость 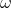 зависит от комбинации степени поворота руля (эквивалентно, радиуса поворота
зависит от комбинации степени поворота руля (эквивалентно, радиуса поворота  ) и поступательной скорости автомобиля
) и поступательной скорости автомобиля  .
.
Чтобы получить поступательную скорость, сегодня переключаемся с обработки видео на датчики движения, которые есть почти в любом смартфоне: GPS приемник, акселерометр и гироскоп. Посмотрим на плюсы и минусы каждого, объединим информацию и получим мгновенную скорость для каждого кадра видео. Более того, информацию о вращениях тоже возьмём с гироскопа, что позволит отказаться от более капризного оптического SLAM и нужной ему калибровки камеры смартфона. В итоге новый процесс сбора данных усох до трех "нажатий кнопки": ставим приложение на телефон — записываем трек на заезде — обрабатываем одной командой на компьютере.
В итоге получаем покадровую аннотацию с поступательной скоростью и скоростью поворотов:
Доступные датчики движения
Работать будем с андроидом. Безотносительно платформы — для знающих английский интересное видео о том, как информация с разных сенсоров может дополнять улучшать калибровку и уменьшать ошибки. Нас интересуют сенсоры движения (акселерометр и гироскоп) и местоположения (GPS).
С точки зрения API всё просто — запрашиваем у пользователя разрешения, подписываемся на обновления, и получаем поток событий с показанием сенсора и временем измерения. Детали можно посмотреть в исходниках.
Рассмотрим плюсы и минусы сенсоров.
GPS
GPS — это, как выяснилось, 90% успеха в определении поступательной скорости, по крайней мере на относительно открытых пространствах. От GPS приходят в формате Location:
- Оценка абсолютного положения (широта, долгота).
- Оценка точности координат — радиус доверительного круга в 68% вокруг оценки. То есть в ~68% измерений настоящее положение устройства должно быть в пределах данного радиуса вокруг оценки. Как правило на более-менее открытом пространстве точность получается в пределах 3-4 м.
- Абсолютная скорость (без направления), оцененная по прошлым замеренным GPS позициям.
Огромный плюс GPS данных — погрешности измерений независимы, то есть не накапливаются со временем: на новое измерение не влияет то, сколько измерений было до этого и скакими погрешностями. Это очень важное свойство, на которое опирается весь остальной подход.
Недостаток же в том, что измерения проводятся редко, примерно 1 раз в секунду, и заметно чаще их проводить просто нет смысла — перемещение устройства всё равно было бы сопоставимо с ошибкой измерения. Как результат, во-первых, GPS данные с запозданием реагируют на изменение скорости, а во-вторых с них сложнее убирать шумы — для этого нужно смотреть на соседние по времени измерения, что ещё больше усугубляет нечеткость данных по времени. Вот пример графика скорости с GPS:
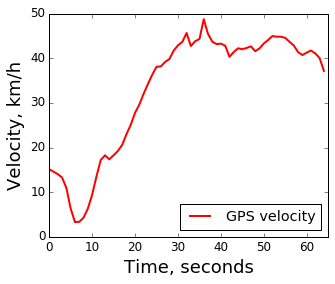
Здесь подозрение вызывают первые 25 секунд (постоянное ускорение и вероятное запаздывание GPS измерений) и шум между 30 и 40 секундой. Для затравки, тот же график после обработки данных с акселерометра и гироскопа:
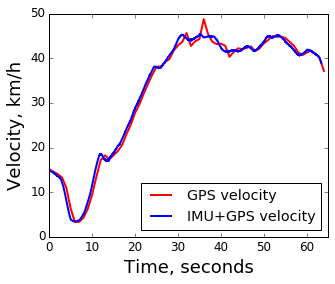
Как видно, есть улучшения по обоим показателям: на ускорения реагируем раньше, и выброс на 35 секунде заглажен.
Инерциальные датчики: акселерометр и гироскоп
Инерциальные датчики замеряют ускорения, линейные (акселерометр) и центростремительные (гироскоп). Результат их измерений — оценка изменения движения устройства по отношению к предыдущему моменту времени. Математически это выражается в использовании системы координат привязанной к устройству:
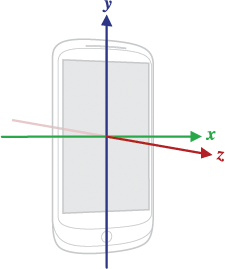
Акселерометр выдает линейные ускорения вдоль трех осей устройства, гироскоп — угловые скорости вокруг тех же трех осей.
Плюс инерциальных датчиков — возможность очень частых измерений, в 400 Гц и выше, что на порядок перекрывает частоту видеокадров в ~30 Гц. Главный минус — отсутствие связи с неподвижной системой координат. Датчики сопособны измерить только изменение относительно предыдущего положения, поэтому для расчета результатов в неподвижной системе координат их показания нужно интегрировать по времени, а при этом ошибки измерений накапливаются — чем дольше период измерения, тем больше итоговая ошибка в следующий момент времени.
Как видно, GPS и инерциальные датчики имеют зеркально противоположные достоинства и недостатки, а значит нужно объединить сильные стороны обоих источников, к чему и приступаем.
Sensor fusion: объединяем информацию
Имея запись данных от GPS и инерциальных датчиков, требуется оценить:
- Абсолютную поступательную скорость с высоким временным разрешением.
- Угловую скорость вращения вокруг вертикальной оси автомобиля (т.е. в плоскости дороги в каждый момент времени).
Горизонтальное вращение мы уже вычисляли в прошлом посте, но, как выяснилось, старый способ (через анализ видео) сложнее и капризнее, чем работа напрямую с гироскопом, поэтому лучше поменять подход.
Поступательная скорость
Казалось бы, чего уж проще. Из школьной физики мы знаем по определению
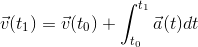
Но нам нужна скорость в неподвижной системе координат, а система координат акселерометра вращается вместе с устройством. Обозначим R матрицу вращения из системы координат устройства в неподвижную, тогда
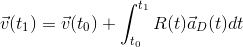
где 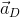 — ускорение по осям координат утсройства. В свою очередь матрицу поворота получаем просто проинтегрировав вращения, измеренные гироскопом (
— ускорение по осям координат утсройства. В свою очередь матрицу поворота получаем просто проинтегрировав вращения, измеренные гироскопом ( — производная матрицы вращения, её можно рассчитать, зная угловые скорости вокруг трех осей):
— производная матрицы вращения, её можно рассчитать, зная угловые скорости вокруг трех осей):

И всё? Не тут-то было, это только для сферического акселерометра в вакууме работает. Посмотрим на реальные данные со смартфона, неподвижно лежащего на столе:
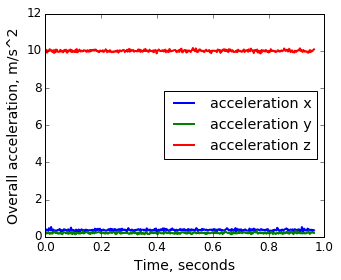
Наблюдения:
- Сила земного притяжения автоматически не вычитается, ведь акселерометр принципиально не может отличать эффект притяжения земли от эффекта ускорения телефона. Значит нужно вручную определять направление и делать поправку. Теоретически андроид предлагает такую поправку на уровне ОС, но на практике у меня оно толком не работало.
- Суммарное ускорение/притяжение по трем осям переваливает за 10 м/с2, что очень далеко от табличных 9.81 м/с2 — за 10 минут набежит 0.2 * 600 = 120 м/с = 432 км/ч.
Второй эксперимент — запишем суммарное ускорение с телефона лежащего на столе экраном вверх, а потом — экраном вниз, и сравним:
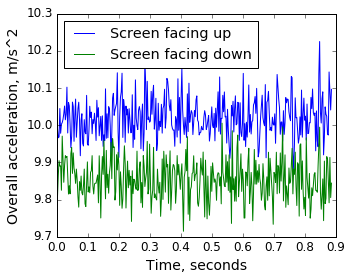
Наблюдения:
- Разница свыше 0.15 м/с2 просто от смены ориентации, то есть присутствует заметная систематическая ошибка в локальной системе координат.
- Постоянный шум измерений в районе 0.05 м/с2, а как видим из интегралов выше — ошибки накапливаются со временем. А когда шумы суммируются, то даже при несмещенном шуме (т.е. когда математическое ожидание измерения совпадает с истинным значением), по центральной предельной теореме дисперсия суммы
nизмерений составит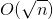 .
.
Модель шума и автокалибровка
Итак, чтобы получить настоящее ускорение в неподвижное системе координат, необходимы поправки к "сырым" измерениям акселерометра. Применим простую модель:
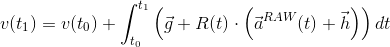
где
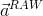 — сырое измерение акселерометра, в системе координат устройства.
— сырое измерение акселерометра, в системе координат устройства.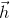 — компенсация систематической ошибки акселерометра, также в системе координат устройства.
— компенсация систематической ошибки акселерометра, также в системе координат устройства.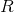 — матрица вращения от системы координат устройства к неподвижной системе координат.
— матрица вращения от системы координат устройства к неподвижной системе координат.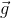 — постоянная сила тяготения в неподвижной системе координат.
— постоянная сила тяготения в неподвижной системе координат.
Матрицу вращения получим интеграцией угловых скоростей с гироскопа, а вот остальные параметры неизвестны (включая 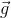 , т.к. неизвестна начальная ориентация смартфона). Найти калибровочные параметры помогут данные с GPS. Вспомним, что измерения GPS довольно точны. А значит скорость, рассчитанная по инерциальным датчикам должна быть близка к скорости по данным GPS. Формализуем эту интуицию как задачу оптимизации. Для каждого интервала между соседними GPS измерениями (порядка 1 секунды) посчитаем дистанцию, пройденную по данным инерциальных данных, и по данным GPS, и целевой функцией назначим метрику L2 по всему времени записи:
, т.к. неизвестна начальная ориентация смартфона). Найти калибровочные параметры помогут данные с GPS. Вспомним, что измерения GPS довольно точны. А значит скорость, рассчитанная по инерциальным датчикам должна быть близка к скорости по данным GPS. Формализуем эту интуицию как задачу оптимизации. Для каждого интервала между соседними GPS измерениями (порядка 1 секунды) посчитаем дистанцию, пройденную по данным инерциальных данных, и по данным GPS, и целевой функцией назначим метрику L2 по всему времени записи:
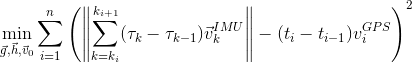
где
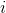 — индекс измерения GPS.
— индекс измерения GPS.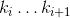 — индексы измерения инерциальных датчиков, попадающих в промежуток между измерениями GPS
— индексы измерения инерциальных датчиков, попадающих в промежуток между измерениями GPS iиi+1.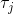 время
время 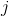 -го измерения инерциальных датчиков.
-го измерения инерциальных датчиков.
Также обозначим 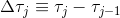 и
и 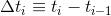 , и подставляя поправки к сырым замерам акселерометра, получаем окончательный вид целевой функции:
, и подставляя поправки к сырым замерам акселерометра, получаем окончательный вид целевой функции:
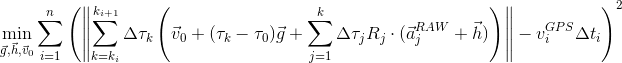
Выглядит страшновато, но на самом деле это простая квадратичная функция, несложно взять производные аналитически и оптимизировать любым численным методом, например L-BFGS.
Для начала проверим на коротком отрезке в полминуты:
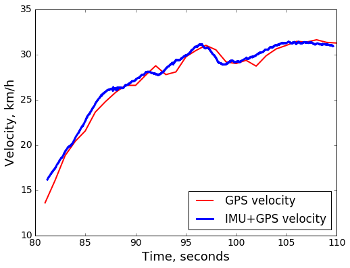
Здесь "на глаз" не очень понятно, какой график более правильный, но можно объявить успех хотя бы в том смысле, что калибровкой удалось подобрать параметры поправок, с которыми оценки скорости с двух разных источников очень близки. Теперь попробуем тот же подход на более продолжительной записи, порядка 10 минут:
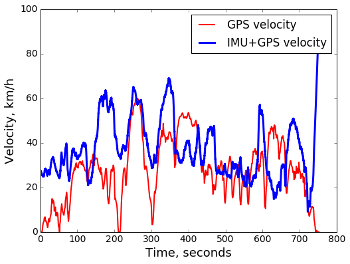
Тут конечно полный провал. Получается, модель простых поправок недостаточна на долгих временных интервалах, то есть остались важные источники искажений, которые она не учитывает. Это могут быть
- Систематические ошибки ("уход") гироскопа.
- Накопленный со временем белый шум акселерометра и гироскопа
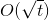 по центральной предельной теореме.
по центральной предельной теореме. - Взаимодействие с вибрациями двигателя (через кузов автомобиля) при движении.
Локальная автокалибровка скользящим окном
Бороться с проблемами простой модели поправок для инерциальных датчиков можно по-разному. Возможные варианты:
- Улучшать точность, моделируя неучтенные источники ошибок (уход гироскопа, накопление белого шума).
- Схитрить.
Мы схитрим. Ведь в конечном итоге нам интересна не сама по себе калибровочная модель, а итоговые значения скорости. А раз на коротких отрезках калибровка справляется, можно применить стандартный прием со скользящим окном:
- разбиваем полный временной интервал на перекрывающиеся короткие отрезки,
- на каждом отрезке отдельно калибруем и вычисляем скорость интегрированием,
- усредняем результат для каждого момента времени по тем отрезкам которые его включают:
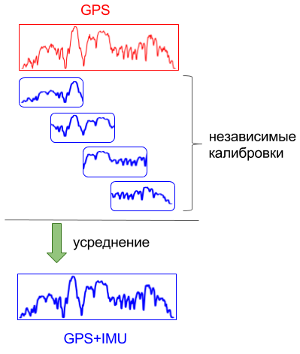
Конечный результат:
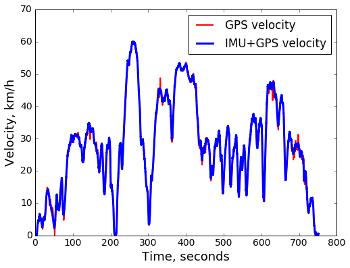
Объявляем успех с поступательной скоростью, возвращаемся к угловой скорости поворотов.
Угловая скорость поворотов
Угловая скорость поворота нужна, чтобы вычислить радиус поворота (и соответственно угол поворота руля): 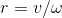 . Гироскоп замеряет угловую скорость напрямую, но в трехмерном пространстве: кроме вращения вокруг вертикальной оси (yaw — собственно поворотов), в данных отражаются еще и вращения вокруг попреречной (pitch — изменение уклона дороги, проезд лежачих полицейских) и продольной (roll — заезд одной стороной в колею или яму):
. Гироскоп замеряет угловую скорость напрямую, но в трехмерном пространстве: кроме вращения вокруг вертикальной оси (yaw — собственно поворотов), в данных отражаются еще и вращения вокруг попреречной (pitch — изменение уклона дороги, проезд лежачих полицейских) и продольной (roll — заезд одной стороной в колею или яму):

Нам нужно выделить из трехмерных вращений только компоненту вокруг вертикальной оси (в системе координат автомобиля). Соответственно, нужно получить направление этой оси. Для этого воспользуемся наблюдением, что величина вращения вокруг вертикальной оси гораздо больше, чем вокруг продольной и поперечной (повороты по 90 градусов — норма, а вот смена уклона и колея — к счастью, нет). А значит можно просто принять ту ось, вокруг которой общее вращение было максимальным, за вертикальную.
Математически выделить доминантную ось вращения удобно, представив каждое элементарное вращение (т.е. измерение гироскопа) в виде кватерниона. Вращение вокруг единичной оси (x,y,z) на угол 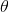 представляется кватернионом
представляется кватернионом

Удобство в том, что первые три компонента кватерниона характеризуют одновременно и направление оси вращения, и величину вращения. Поэтому хороший результат дает метод главных компонент, примененный просто к первым трем компонентам кватерниона. После выделения доминантной оси, получается такая картина:
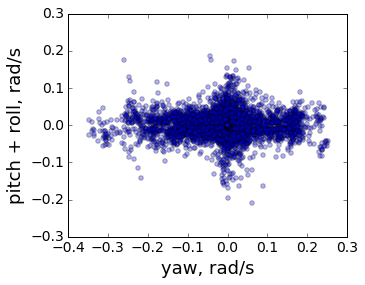
Видно, что заметно большая доля вращений проходит вокруг выделенной доминантной оси, чем вокруг остальных двух перпендикулярных ей.
Кстати, в предыдущем посте тоже применялся метод главных компонент, но тогда я не сообразил применить его к вращениям напрямую, а выделял горизонтальную плоскость по трехмерной траектории (т.е. основываясь на смещениях вместо вращений). Новый способ лучше не только тем, что полностью не нуждается в информации о смещениях, но и тем, что вертикальная ось выделяется в системе координат устройства. То есть с новым подходом вертикальная ось — перпендикуляр к локальной плоскости дороги, вместо средней плоскости всей траектории в старом подходе. Например, теперь вертикальная ось поворачевается (вместе с автомобиле при переезде от дороги в гору к дороге под гору). В результате выделение горизонтального поворота из общего вращения стало точнее.
Данные
Бонусом к коду хочу поделиться уже обработанными данными для тех, кому интересно поиграться с обучением своих моделей. В торренте больше часа сырых данных, записанных на подмосковных дорогах, плюс (в директориях postprocessed) результаты вычисления поступательной скорости и угловой скорости поворотов. Если воспользуетесь — будет интересно узнать о результатах!
На этом всё, в следующей серии — учимся предсказывать управляющие воздействия по видео.
Автор: waiwnf






