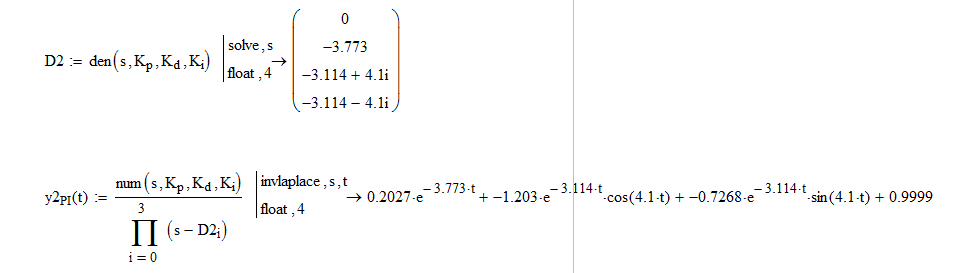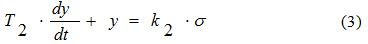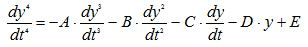В поисках простой модели ПИД регулятора с объектом
Моделированию работы ПИД регулятора посвящено большое количество публикаций в сети. Лидирует проектирование моделей ПИД регулятора с применением Matlab Simulink [1,2] (134 миллиона ссылок в yandex). Сам процесс создания модели какой-то однообразный. В модель переносят всё новые и новые блоки. Одно движение ручного манипулятора и нате вам ПИД контролер, ещё одно и вот передаточная функция объекта. Соединяешь блоки, настраиваешь параметры, готовишь вычислитель. Да, возможностей много, но как-то слишком всё искусственно. И уже становится совсем непонятным к чему тут дифференциальные уравнения, методы их решения и то операционное исчисление, которым долго морочили голову. Ищу реализацию ПИД в Mathcad, тут ссылок в том же yandex, поменьше, всего то 81 миллион, а математики и формул побольше. Рассматриваю пример ПИД, поставляемый вместе с пакетом Mathcad 14.
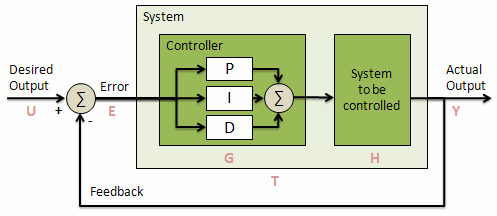
В качестве объекта колебательное звено. Много умных объяснений, но в итоге два оператора laplace и invlaplace. Общая передаточная функция имеет в числителе вторую степень оператора, а в знаменателе четвёртую. Чтобы операторы laplace и invlaplace сработали, когда подключены все три составляющих ПИД, находят ещё и корни знаменателя передаточной функции, эти корни комплексно сопряжённые.
Теперь ищу реализацию ПИД на Python. Тихо радовался 97 миллионам результатов, но не долго. О Python 2.7 только применительно к прошивке Arduino на примере ESP32. Но и это переполняет сердце гордостью за Python.
Разочаровавшись в поиске, решил написать модель сам, в меру своих более чем скромных возможностей.
Структурная схема объекта управления
Постановку задачи взял из [3], в ней меня привлекло разнообразие структуры объекта регулирования. По ходу исправил несколько ошибок. Так, в конечном дифференциальном уравнении был потерян квадрат при T2, данные таблицы для a2 не соответствовали результатам аппроксимации. Кроме того, ввёл установку управления в виде единичного бесконечного импульса, чтобы оживить картинку переходного процесса. Уж как-то не естественно для ПИД регулятора она выглядит в [3].
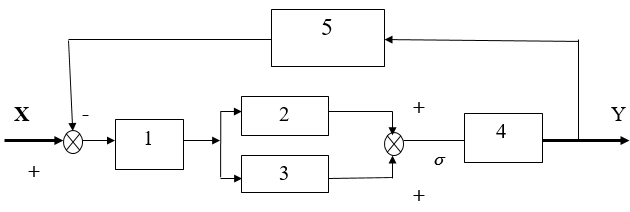
Будем исследовать систему регулирования со следующей структурной схемой.
- Колебательное звено [4] описывается дифференциальным уравнением второго порядка.
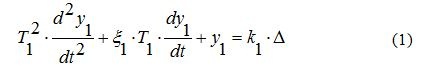
- Линейное статическое звено, определяющие зависимость выхода от входа которого определяется по табличным данным. Данные могут быть получены экспериментальным путём. Из-за погрешностей снятия данных, следует применять линейную аппроксимацию
.
- Второе линейное статическое звено — зависимость выхода от входа определяется по табличным данным, которые могут быть получены экспериментальным путём.. Из-за погрешностей снятия данных, следует применять линейную аппроксимацию
.
- Линейное динамическое звено, на вход которого поступает сума сигналов от блоков 2,3
Звено имеет передаточную функцию, которая описывается линейным дифференциальным уравнением первого порядка.
- ПИД регулятор с известным законом регулирования, при котором для настройки на объект регулирования используются коэффициент пропорциональности
при линейной функции, коэффициент дифференцирования
при первой производной и коэффициент интегрирования
при неопределённом интеграле.
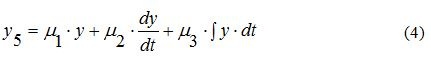
Единичное входное воздействие 1(t) преобразуется в операторную форму как 1 / p. Переведём в операторную форму уравнения 1,4 в результате получим.
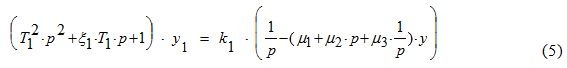
Продифференцируем обе части (5), для этого просто умножим на оператор p, получим.
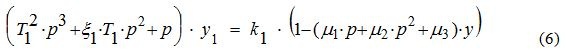
Переведём в операторную форму уравнения (2), (3) и выразим y(y1).
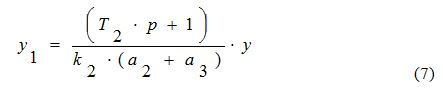
Подставим (7) в (6) получим:
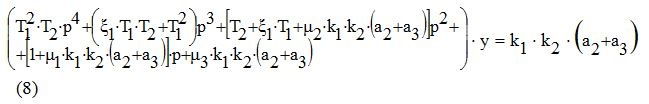
Перейдём (8) во временную область, для этого операторную форму заменим дифференциальным уравнением.
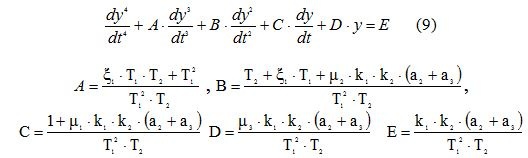
Решение задачи определения настроек ПИД регулятора на Python
Зададим следующие параметры объекта регулирования:
T1=7.0; T2=5.0; s=0.4; k1=5.5; k2=5.5. Данные для аппроксимации характеристик звеньев 2,3 сведём в таблицу.
Отставим объект без регулятора, для этого примем 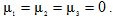
#!/usr/bin/python
# -*- coding: utf-8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def mnkLIN(x,y,q): # аппроксимация характеристик статических объектов МНК
a=round((len(x)*sum([x[i]*y[i] for i in range(0,len(x))])-sum(x)*sum(y))/(len(x)*sum([x[i]**2 for i in range(0,len(x))])-sum(x)**2),3)
b=round((sum(y)-a*sum(x))/len(x) ,3)
y1=[round(a*w+b ,3) for w in x]
s=[round((y1[i]-y[i])**2,3) for i in range(0,len(x))]
sko=round((sum(s)/(len(x)-1))**0.5,3)
if q==1:
plt.subplot(221)
plt.plot(x, y, color='r', linewidth=2, marker='o', label='Коэффициент a= %s'%str(a))
plt.plot(x, y1, color='g', linestyle=' ', marker='o', label='СКО =%s'%str(sko))
plt.legend(loc='best')
plt.grid(True)
else:
plt.subplot(222)
plt.plot(x, y, color='r', linewidth=2, marker='o', label='Коэффициент a= %s'%str(a))
plt.plot(x, y1, color='g', linestyle=' ', marker='o', label='СКО =%s'%str(sko))
plt.legend(loc='best')
plt.grid(True)
return a
T1=7.0;T2=5.0;s=0.4;k1=5.5;k2=5.5# параметры объекта регулирования.
x=[0,1,2,3,4,5]
y=[0,-11,-22,-33,-44,-55]
a2=mnkLIN(x,y,1)
x=[0,1,2,3,4,5]
y=[0,17,34,51,68,85]
a3=mnkLIN(x,y,2)
#m1=0.5;m2=2.0;m3=0.3# параметры ПИД регулятора.
m1=0.0;m2=0.0;m3=0.0
a=a2+a3
A=round((s*T1*T2+T1**2)/(T1*T2**2),3)
B=round((T2+s*T1+k1*k2*m2*a)/(T1*T2**2),3)
C=round((1+k1*k2*m1*a)/(T1*T2**2),3)
D=round(k1*k2*m3*a/(T1*T2**2),3)
E=round(k1*k2*a/(T1*T2**2),3)
def f(y, t):# решение дифференциального уравнения системы регулирования.
y1,y2,y3,y4 = y
return [y2,y3,y4,-A*y4-B*y3-C*y2-D*y1+E]
t = np.linspace(0,100,10000)
y0 = [0,1,0,0]#начальные условия
w = odeint(f, y0, t)
y1=w[:,0] # вектор значений решения
y2=w[:,1] # вектор значений производной
plt.subplot(223)
plt.plot(t,y1,linewidth=1, label=' p- %s,d- %s,i- %s,'%(str(m1),str(m2),str(m3)))
plt.ylabel("z")
plt.xlabel("t")
plt.legend(loc='best')
plt.grid(True)
plt.show()
Результат роботы программы.
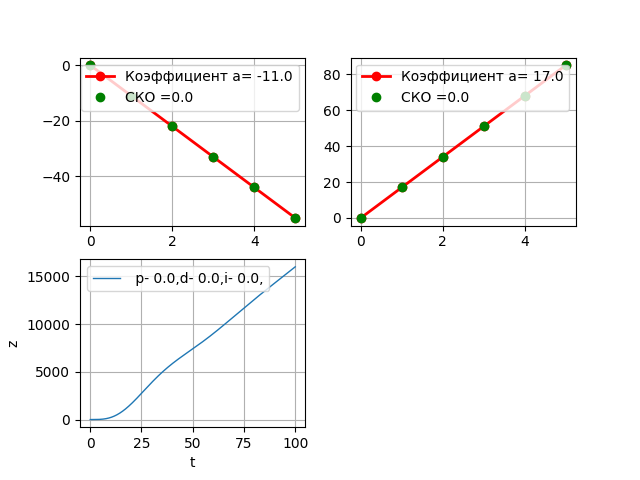
Без ПИД регулятора объект пошёл в «разнос». После предварительного подбора параметров ПИД получим.
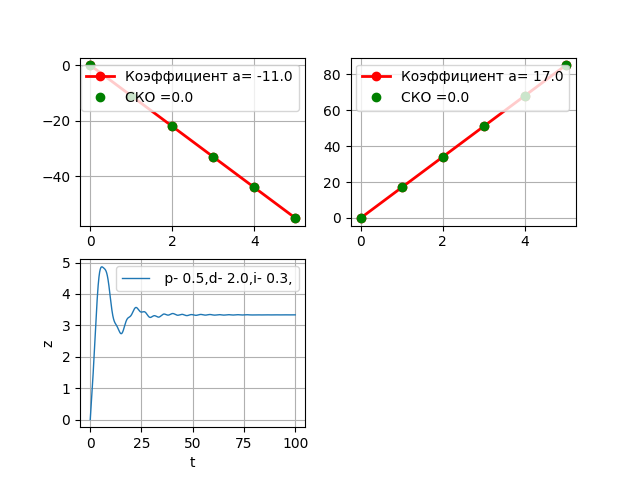
Изменим табличные данные для третьего звена, увеличим а3 в два раза.
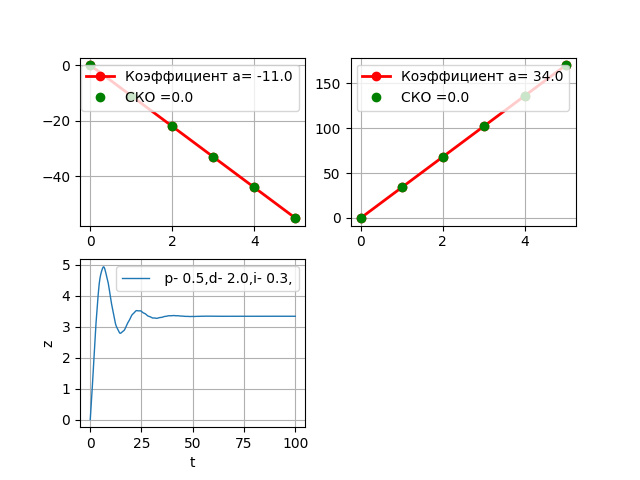
Регулятор стабилен.
Выбор функции для решения уравнения (9) на Python и сравнение результатов с решением на Matcad
Я использовал функцию odeint из библиотеки scipy. Integrate.
def f(y, t):# решение дифференциального уравнения системы регулирования.
y1,y2,y3,y4 = y
return [y2,y3,y4,-A*y4-B*y3-C*y2-D*y1+E]
t = np. linspace(0,100,10000)
y0 = [0,1,0,0]#начальные условия
w = odeint(f, y0, t)
y1=w[:,0] # вектор значений решения
y2=w[:,1] # вектор значений производной
Если уравнение (9) перестроить так, чтобы в левой части была производная высшего порядка, а в правой всё остальное, то получим.
Так и строится функция def f (y, t). Функция odeint имеет три обязательных аргумента и выглядит вот так odeint (func, y0, t[,args=(), ...]).
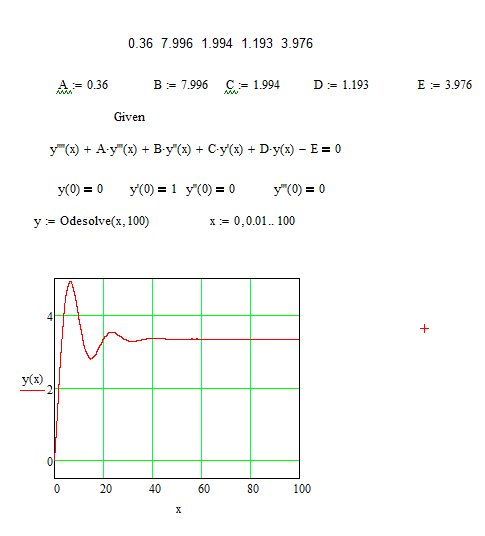
Для сравнения выведем используемые в приведенной функции def f (y, t) значения переменных A, B, C, D, E, получим 0.36 7.996 1.994 1.193 3.976. Составим на Mathcad 14 программу для решения дифференциального уравнения (9) и построим переходную характеристику.
Графики и числовые значения полностью идентичны. Таким образом, функции Odesolve Mathcad и odeint Python дают одинаковые численные решения приведённой в статье задачи.
Вывод
На данном этапе развития язык программирования Python с библиотеками SciPy и NumPy может эффективно использоваться для численного моделирования контуров автоматического регулирования содержащих динамические и статические звенья.
Ссылки
- Автоматизированная настройка ПИД-регулятора для объекта управления следящей системы с использованием программного пакета MATLAB Simulink Филиппов А. В.1, Косолапов М. А.2, Маслов И. А.3, Тарасова Г. И.
- Методы настройки ПИД-регулятора в matlab simulink.
- Подбор ПИД регулятора.
- Модель колебательного звена в режиме резонансных колебаний на Python.
Автор: Scorobey