Главная

Обучение с подкреплением на примере игры «крестики-нолики»

2017-05-02 в 7:11, admin, рубрики: Q-learning, машинное обучение

«Крестики-нолики» — игра изученная вдоль и поперек, и разработка ИИ для неё может свестись к организации дерева решений описанного в Википедии. В данной статье будет рассмотрено решение игры с помощью обучения с подкреплением и аппроксимацией функций ценности.

Поготовка

Примем следующие правила:

Агент ходит первым и играет «крестиками».
Агент будет принимать только решения имеющие максимальную ценность.
С 5% вероятностью агент будет принимать зондирующие решения.
Только в случае выйгрыша агента, он получает вознаграждение.

Следующим этапом необходимо подготовить функцию ценности для агента. В нашем случае, функцией ценности будет являться таблица состояний игры, в которой значение от 0 до 1 будет указывать что то или иное состояние «лучше» другого. Изначально зададим в нашей таблице что все выйгрышные комбинации (три крестика в ряд, столбец или по диагонали) дают вероятность выйгрыша равна 1. Аналогично, всех состояний с тремя нулями будет вероятность выйгрыша равна 0. Для всех прочих состояний вероятность 0,5.

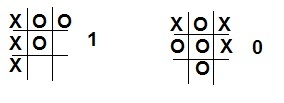
С целью упрощения составления таблицы вероятностей примем, что всего

$$display$$3^9=19683$$display$$

состояний. Конечно же, половина этих комбинаций невозможна, но и оптимизации кода в целях не стояло.

Код иницализации таблицы вероятностей

float V[19683]; 

//-------

void setV(int a1,int a2,int a3,int b1,int b2,int b3,int c1,int c2,int c3,float v)

{

int num;

num = ((((((((a1*3)+a2)*3+a3)*3+b1)*3+b2)*3+b3)*3+c1)*3+c2)*3+c3;

V[num] = v;

}

//-------

for (int i1=0;i1<3;i1++)

for (int i2=0;i2<3;i2++)

for (int i3=0;i3<3;i3++)

for (int i4=0;i4<3;i4++)

for (int i5=0;i5<3;i5++)

for (int i6=0;i6<3;i6++)

for (int i7=0;i7<3;i7++)

for (int i8=0;i8<3;i8++)

for (int i9=0;i9<3;i9++)

{

setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0.5);
if (i1==i2 && i2==i3 && i3==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i4==i5 && i5==i6 && i6==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i7==i8 && i8==i9 && i9==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i1==i5 && i5==i9 && i9==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i7==i5 && i5==i3 && i3==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i1==i4 && i4==i7 && i7==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i2==i5 && i5==i8 && i8==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i3==i6 && i6==i9 && i9==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1);

if (i1==i2 && i2==i3 && i3==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i4==i5 && i5==i6 && i6==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i7==i8 && i8==i9 && i9==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i1==i5 && i5==i9 && i9==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i7==i5 && i5==i3 && i3==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i1==i4 && i4==i7 && i7==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i2==i5 && i5==i8 && i8==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i3==i6 && i6==i9 && i9==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); }

Ход игры

Оппонетном будет являться человек, который соответственно будет играть за нолики и периодически поддаваться. В ходе игры будет происходить изменение ценности ее состояний. Для того, чтобы правильно оценить действия агента, необходимо записывать последовательность тех состояний, которые он выбрал и по окончании игры перерасчитать их. Формула расчета ценности V(s) будет иметь следующий вид:

$inline$V(s) = V(s) + A*[V(s') - V(s)]$inline$,

где А — размер шага, влияющего на скорость обучения. V(s') — ценность действия по окончанию игры (1 — если выйграл, 0 — иначе).

Размер шага влияет на то, будет ли меняться стратегия оппонента или нет. Если необходимо учитывать изменчивость стратегии, то необходимо оставить размер шага константой. Иначе при уменьшении шага до нуля агент остановит свое обучение.

Использование зондирующих ходов (не имеющих высокую ценность) позволяет проверить состояния, которые ввиду высокой ценности других ходов никогда бы не исполнились, что дает небольшой шанс на изменение стратегии в выйгрышную сторону.

Код выбора хода агента

void stepAI(void)

{

int flag;

c_var=0;

for (int i=0;i<19683;i++)

 {

 flag=0;

 readMap(i);

 for (int j=1; j<10;j++)

 if (rm[j]!=m[j])

 if ((m[j]==0) && (rm[j]==1)) flag++;

 else flag+=2;

 if (flag==1) {

 var[c_var]=i;

 c_var++;

 }

}

float v_max;

int v_num_max;

if (random(100)<5) v_num_max=random(c_var);

else {

 v_max = V[var[0]];

 v_num_max = 0;

 if (c_var>1)

 for (int i=1;i<c_var;i++)

 if (V[var[i]]>v_max)

 v_num_max = i;

 }
steps++;

steps_m[steps]=var[v_num_max];

readMap(var[v_num_max]);

for (int i=1;i<10;i++)

 m[i]=rm[i];

paintMap(); }

В выше расположенном коде происходит отбор возможных ходов (состояния в которых элементы идентичны текущему состоянию поля, а также присутствует еще один крестик). Затем из полученных состояний выбирается либо произвольный ход (с вероятностью 5%), либо «жадный» ход (с максимальной ценностью). По окончании выбора, данный ход записывается в отдельный массив сделанных ходов.

По окончании игры происходит как уже сказано перерасчет ценности сделанных ходов.

Перерасчет ценности

void learnAI(int res)

{

for (int i=0;i<steps;i++)

 V[steps_m[i]] += A * (res - V[steps_m[i]]);

A -= 0.01;

}

Итог

→ Программа и проект в С++ Builder 6

В данном примере был кратко рассмотрен один из аспектов обучения с подкреплением. Если обычно агент контактирует со средой, то в данном примере обучение осуществлялось с игроком-противником. Хотя этот пример довольно прост, может показаться что данный метод на других примерах будет очень ограничен чем это есть на самом деле.