Как мы знаем, любое плывущее в жидкости тело рано или поздно остановится за счет сил вязкого трения, если его движение не поддерживается каким-нибудь двигателем. Но есть жидкости, называемые сверхтекучими, в которых вязкое трение отсутствует(*). Самый известный пример сверхтекучей жидкости – это жидкий гелий, охлажденный, как минимум, до 2.17 градусов выше абсолютного нуля температуры.
Движение при полном отсутствии вязкости проявляется во многих впечатляющих эффектах: сверхтекучий гелий легко протекает через самые узкие щели и трещины, способен бесконечно течь по кругу(**) и вытекать из сосуда через тончайшую жидкую пленку, налипшую на его стенки. Все эти явления – примеры крупномасштабных квантовых эффектов.
В недавней теоретической статье был рассмотрен вопрос: можно ли плавать в сверхтекучей жидкости? Иными словами, может ли гипотетический пловец, двигая руками и ногами, создавать силу тяги, позволяющую ему разгоняться или замедляться, не задействуя силы вязкого трения?
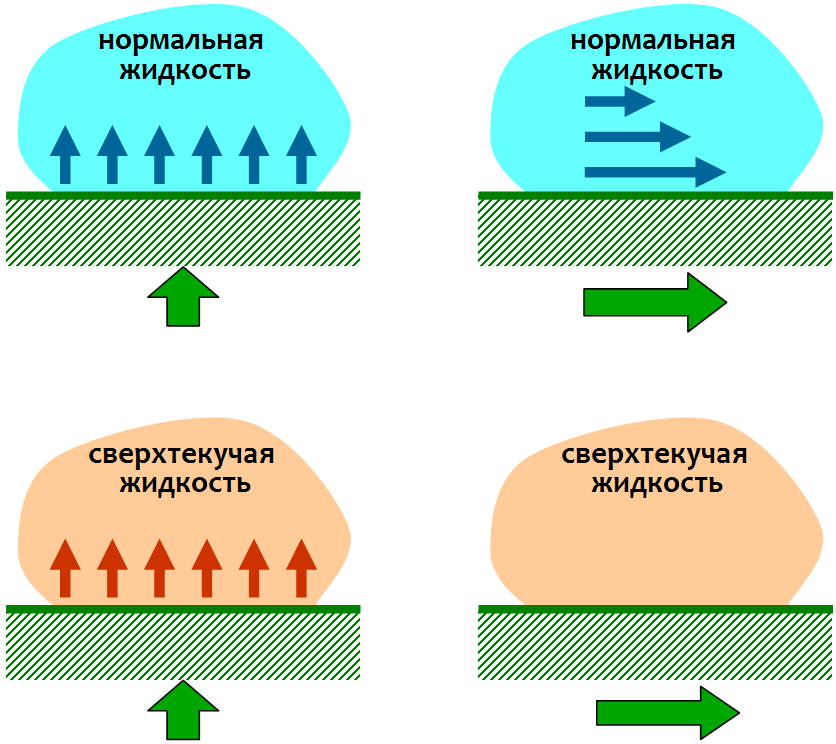
Осознать нетривиальность ответа на этот вопрос можно, рассматривая поведение нормальной и сверхтекучей жидкостей при взаимодействии с телами. Как показано на рисунке, нормальную жидкость можно заставить двигаться, как толкая ее поверхностью твердого тела, так и увлекая ее за собой за счет сил вязкого трения. В сверхтекучей жидкости последнее не получится: трение в ней отсутствует, и ее можно только толкать, что, как мы увидим, делает невозможным некоторые способы плавания.
Для анализа общих принципов физических явлений принято рассматривать простые модели «сферических коней в вакууме». Обсуждаемая статья не является исключением: в ней были рассмотрены двухтельный и трехтельный модельные «пловцы», представляющие собой два и три эллипсоида, соединенных «суставами». Пловцы могут двигать своими эллипсоидами, сгибая и разгибая суставы. Если у пловца получится отталкиваться от окружающей жидкости, он создаст силу тяги и начнет двигаться.
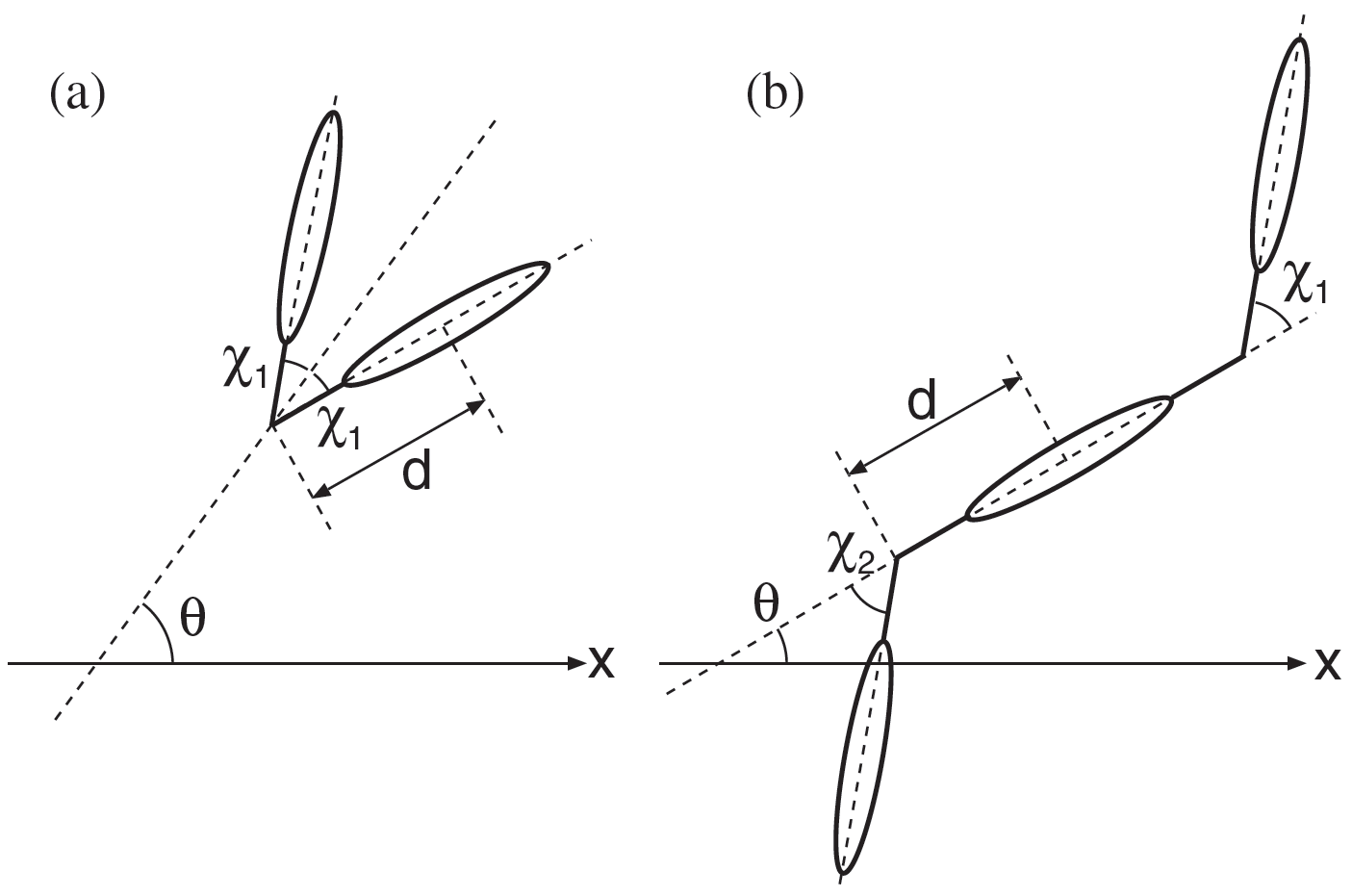
Двухтельный пловец похож на двустворчатого моллюска и может пытаться плыть, периодически изменяя угол между своими эллипсоидами подобно машущей крыльями бабочке. Однако расчеты показывают, что плыть у него не получится: при взмахах пловец перемещается вперед и назад, но в среднем остается на месте (здесь можно посмотреть видео его незамысловатых движений).
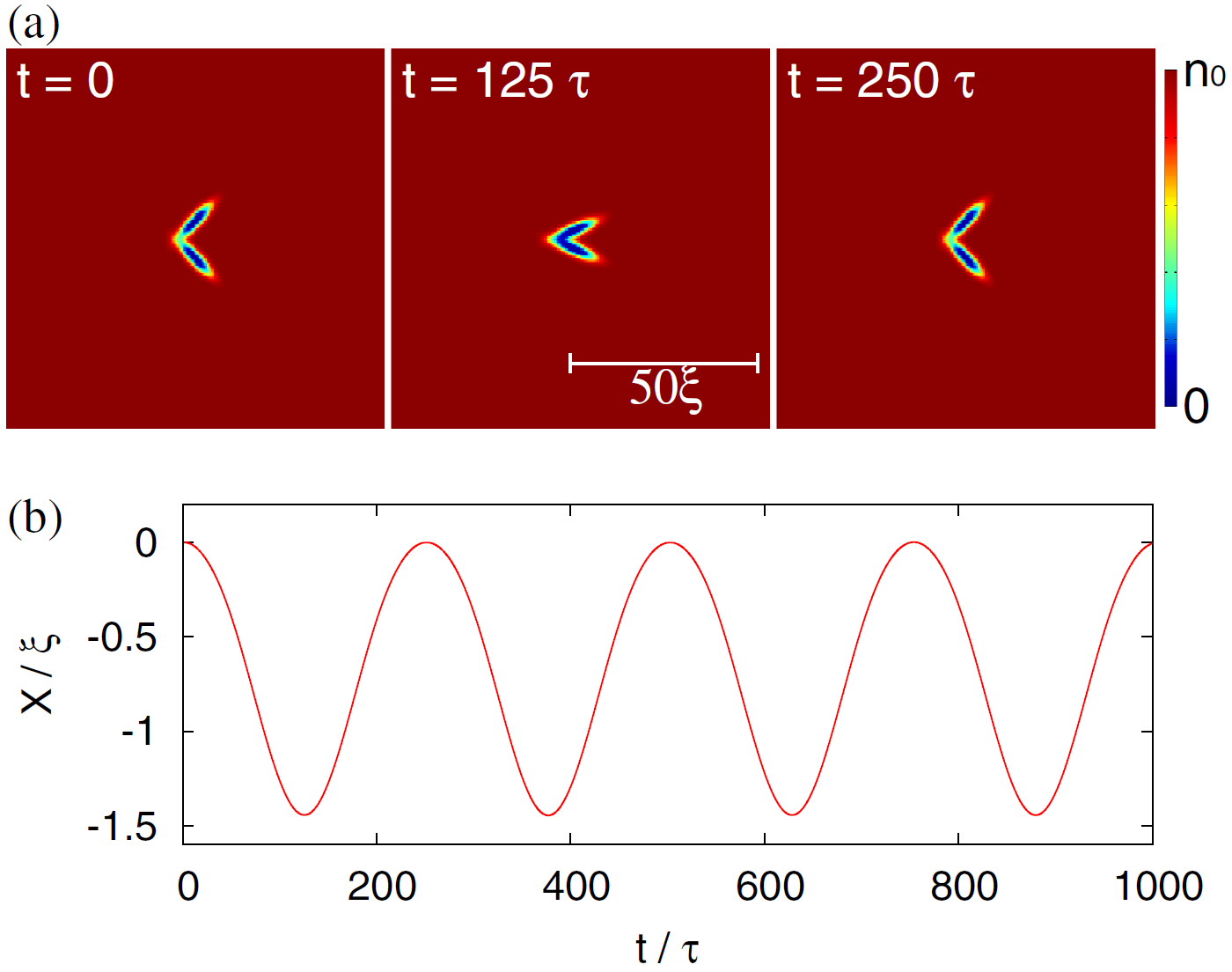
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды двухтельного пловца.
Внизу: координата пловца как функция времени.
Можно провести параллели между этим результатам и теоремой Пёрселла о морском гребешке (Purcell’s scallop theorem). Эта важная теорема теории плавания гласит, что двустворчатый моллюск, медленно открывающий и закрывающий свою раковину в вязкой жидкости, не будет никуда плыть, коль скоро его движения будут обратимы во времени. Последнее означает, что периодические открывания и закрывания створок раковины не меняют свой вид при запуске времени в обратном направлении (можно представить себе видеоролик, выглядящий просмотре задом наперед точно так же, как при нормальном воспроизведении). В нашем случае жидкость не имеет вязкости, и работает не сама теорема Пёрселла, а ее аналог для сверхтекучей жидкости.

Рисунок из доклада Эдварда Пёрселла (лауреата Нобелевской премии по физике в 1952 году).
Ситуация меняется, когда двухтельный пловец начинает размахивать своими эллипсоидами с большей частотой. Если скорость их движения превышает скорость звука в жидкости, начинают испускаться звуковые волны и вихри(***). Эти возбуждения уносят с собой некоторый импульс, который, за счет отдачи, заставляет пловца двигаться. На рисунке видно, что в этом случае его координата хоть и колеблется, но с течением времени в целом уменьшается, а это значит, что пловец движется справа налево. После десяти колебаний (справа от пунктирной линии на графике) взмахи створками прекращаются, и пловец продолжает двигаться по инерции (видео).
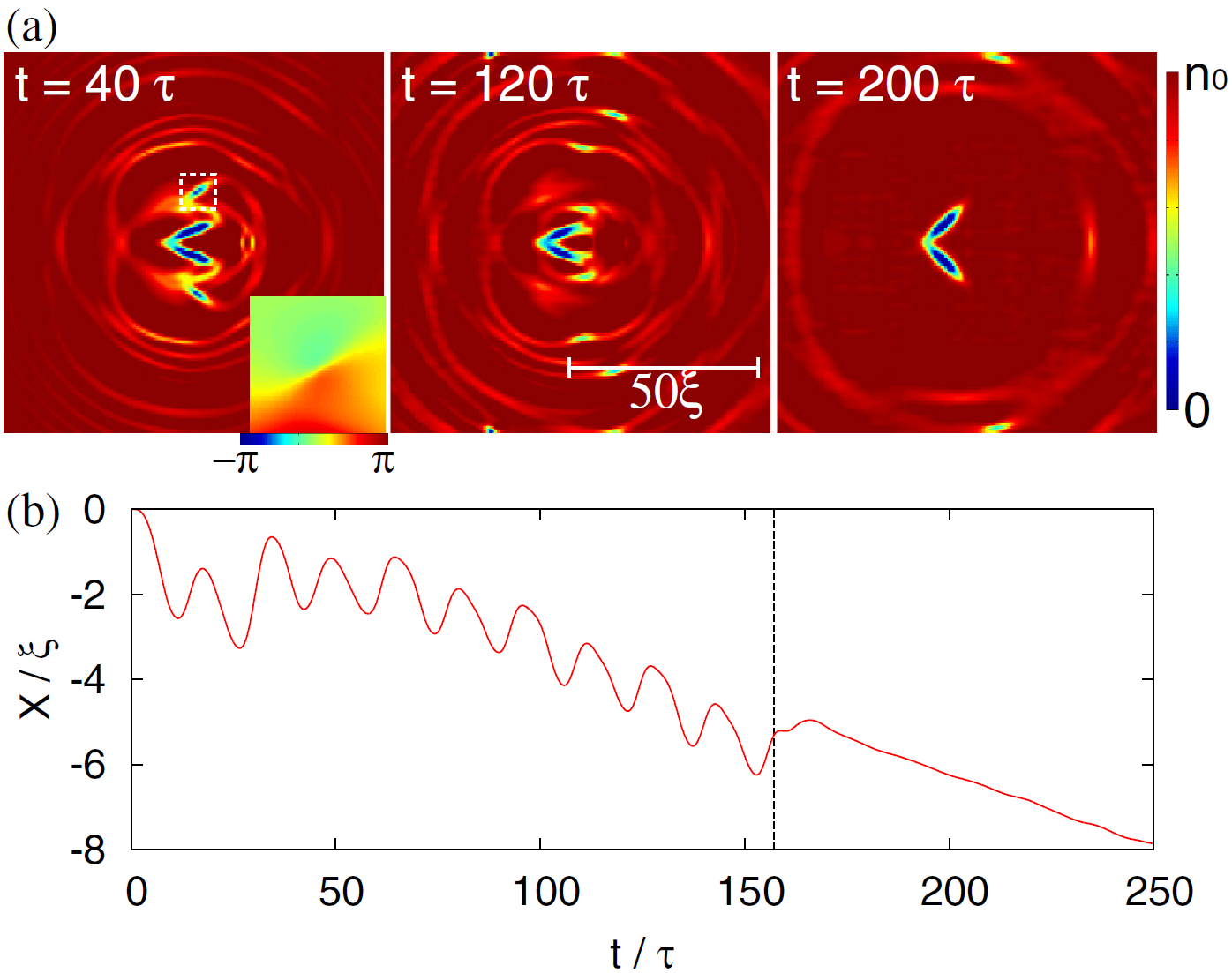
Можно попробовать и другой тип движения пловца, когда его створки смыкаются и раздвигаются не только в правом направлении, а попеременно в двух направлениях. Такие симметричные движения похожи на взмахи крыльев бабочки. Расчеты показывают, что при этом возбуждается много квантованных вихрей (они видны на рисунке как маленькие кружочки), но, в целом, плавание не очень эффективно. Причина в том, что возбуждается примерно одинаковое количество вихрей, движущихся как вправо, так и влево, и уносимые ими импульсы в значительной мере компенсируют друг друга (видео).
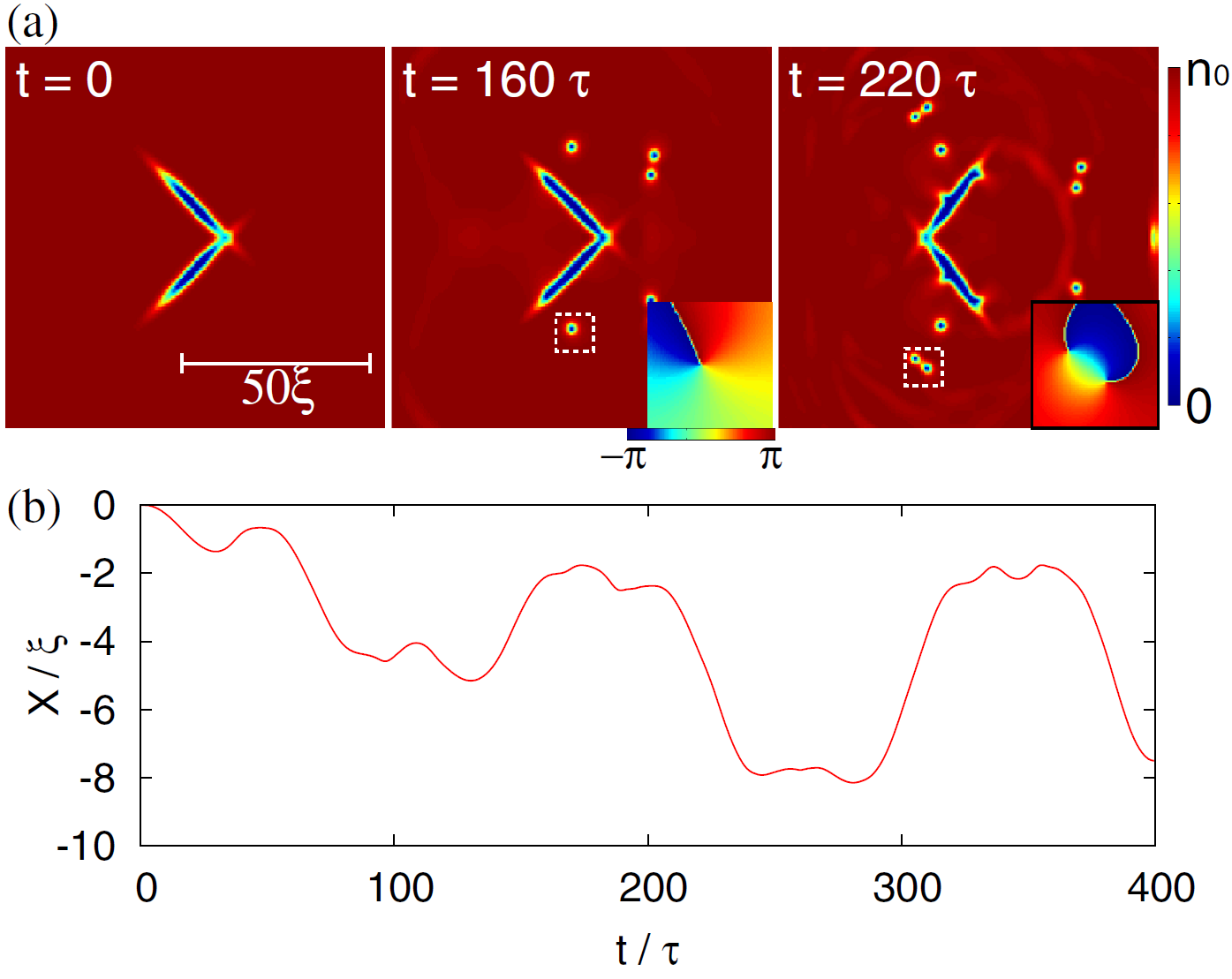
Рассмотрим теперь трехтельного пловца. Перед двухтельным у него есть важное преимущество: он может извиваться, совершая змеевидные движения, которые не переходят сами в себя при обращении времени. А значит, теорема Пёрселла к нему неприменима, и он должен плыть даже при медленных движениях. Приведенные на рисунке расчеты подтверждают эту догадку: при извивающихся движениях пловец уверенно продвигается по горизонтали, при этом немного смещаясь и по вертикали (видео).
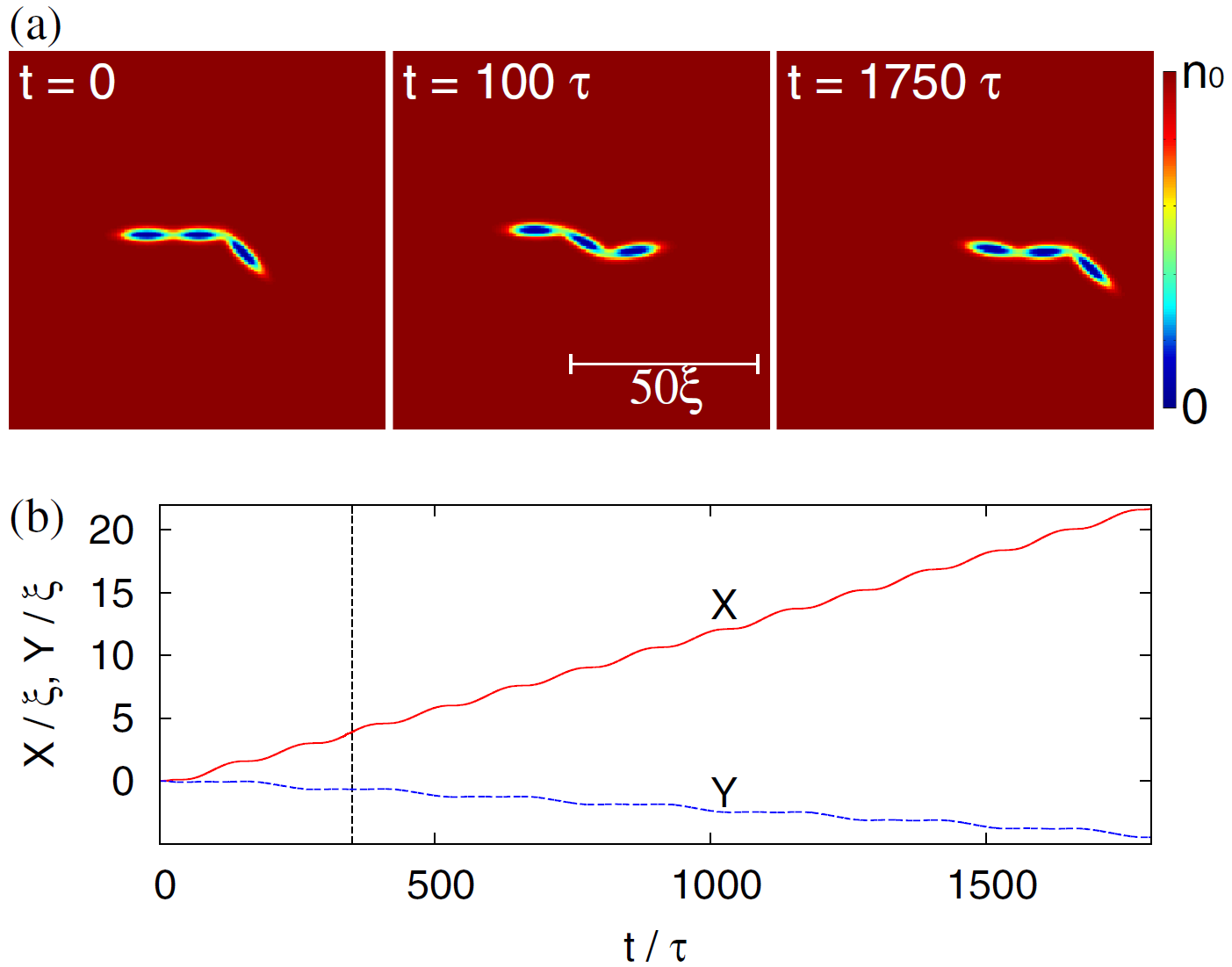
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды трехтельного пловца.
Внизу: горизонтальная (X) и вертикальная (Y) координаты пловца как функции времени.
Какое применение можно найти полученным результатам? Казалось бы, задача о плавании в сверхтекучей жидкости не особо актуальна на практике, но есть одна область, где она может быть полезной. В последнее время активно развиваются эксперименты с бозе-конденсацией и сверхтекучестью ультрахолодных атомных газов, с которыми связывают большие планы по созданию квантовых симуляторов, квантовых компьютеров и экспериментальному моделированию экзотических состояний материи. В таких системах можно создавать сгустки сверхтекучего газа одного вида, погруженные в сверхтекучий газ другого вида. Если мы сможем деформировать сгусток так, как нам нужно (а это можно делать с помощью лазерных лучей), то можно будет заставить этот сгусток плыть, отталкиваясь от окружающего газа. На рисунке показаны расчеты, демонстрирующие такую возможность: когда изменения формы сгустка не являются обратимыми во времени, ему действительно удается двигаться (видео).
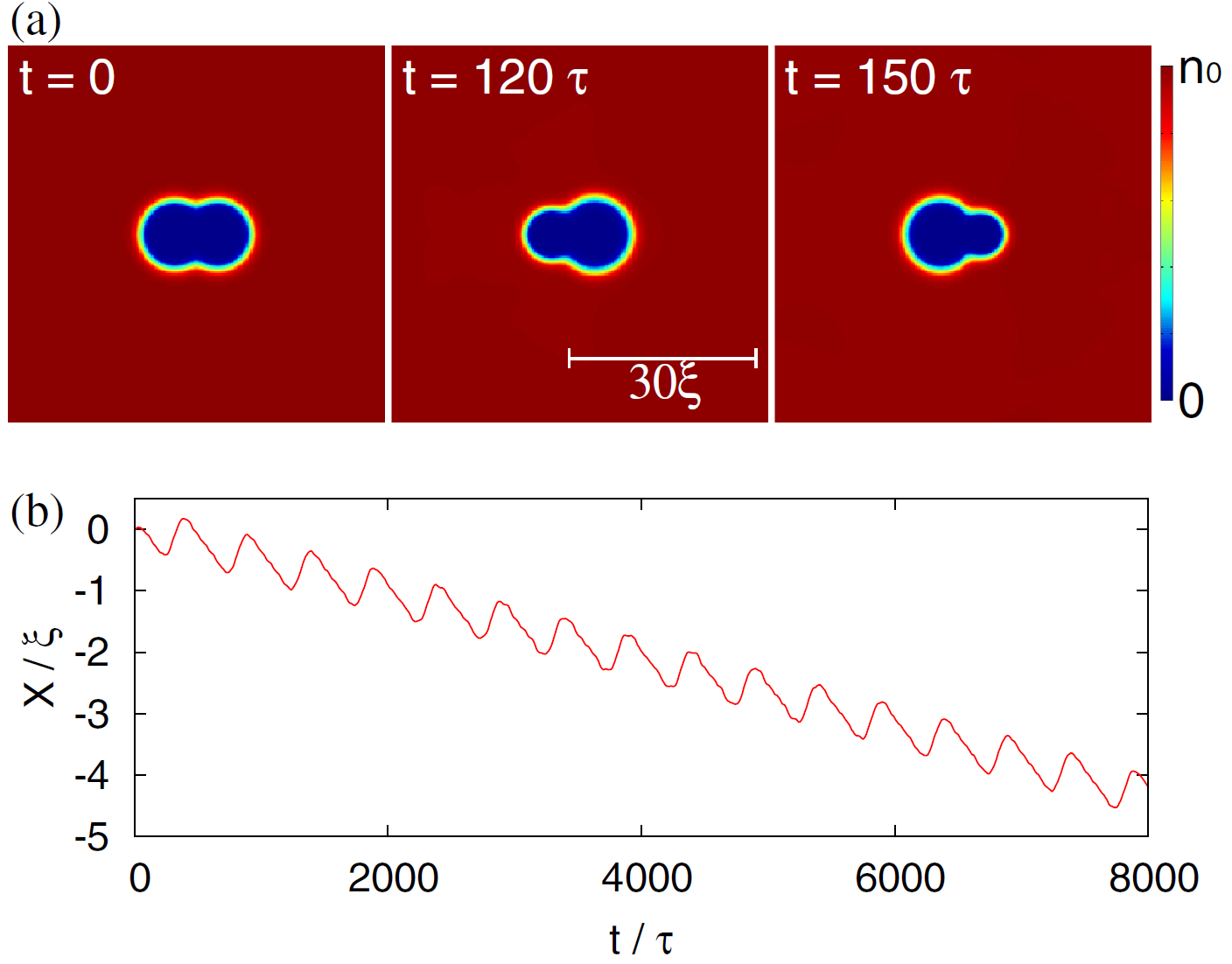
Итак, мы видим, что плавать в сверхтекучей жидкости нужно с умом: теорема Пёрселла гарантирует, что мы не сможем плыть, если наши движения руками и ногами будут совпадать с самими собой при проигрывании в обратном направлении. Чтобы начать перемещаться, нам нужно будет либо двигаться быстрее звука (что проблематично), либо извиваться подобно змее, нарушив обратимость движений во времени. Эти выводы хорошо знакомы плавающим в вязкой жидкости микроорганизмам: для того, чтобы обойти теорему Пёрселла, им приходится использовать спирально вращающиеся жгутики, являющиеся аналогами рассмотренного здесь трехтельного пловца.
По материалам статьи:
Hiroki Saito, Can We Swim in Superfluids?: Numerical Demonstration of Self-Propulsion in a Bose–Einstein Condensate, Journal of the Physical Society of Japan 84, 114001 (2015).
(*)На самом деле, это не совсем так: любая реальная сверхтекучая жидкость может быть представлена как совокупность «нормальной» и сверхтекучей компонент (двухжидкостная модель), и нормальная компонента будет по-прежнему замедлять движущееся тело. Однако это не мешает сверхтекучей компоненте двигаться полностью без трения.
(**)На практике круговой поток сверхтекучего гелия может затухать, но не из-за вязкости, а за счет квантовомеханического процесса – проскальзывания квантованных вихрей. В экспериментах не наблюдалось никакого заметного затухания в течение 18 часов.
(***)Возникающие в сверхтекучей жидкости вихри – это не просто вихри наподобие маленьких торнадо, а квантованные топологические возбуждения. В отличие от обычных вихрей, они не могут просто исчезнуть за счет постепенного затухания потока.
Автор: PhysRevB




